局部语言的代数结构——关于局部语义的一些一般性观察（1）*

查非

南开大学哲学院

zhafei@nankai.edu.cn

局部语言的代数结构
——关于局部语义的一些一般性观察（1）*

查非

南开大学哲学院

zhafei@nankai.edu.cn

在模态逻辑中，出于构造有穷模型这一特殊动机，用于构造过滤的公式集被设计成对所有子公式封闭的。事实上，仅就构造过滤模型而言，一个布尔代数可以经由非独立的生成子生成，因此公式集对子公式封闭是不必要的。运用子代数域的封闭算子，我们可以在命题逻辑的意义上定义一种贯彻了D.M.Armstrong的Combinatorialism本体论的可能世界模型。我们姑且称相应的理论为局部语义。不难发现，局部语义可以被应用于大多数涉及到信念状态，上下文语境的哲学逻辑领域以及人工智能领域。

局部；语境；过滤；布尔代数

1 引言

在模态逻辑中，出于构造有穷模型这一特殊动机，用于构造过滤的公式集Γ被设计成对所有子公式封闭的。抛开构造有穷模型这个动机本身，过滤提供了一种构造模型的方法：一个模型的过滤只为语言中的一部分表达式提供解释，使得这部分表达式在语言中形成了一个独立的部分，姑且称之为当前语言的一个局部。现在，根据经典定义，Γ相对于子公式的封闭性要求语言的局部只能在命题变元集上被划定。

众所周知，关于自然语言的语义，存在着整体主义和原子主义之间的争议。而通过过滤划定的语言局部可以视为形式语言的某种功能上的局部。现在抛开语义整体论的问题，但就形式化工作而言，我们是否有必要在设计一种形式语言的时候设法使得全体符号或者全体合式公式中的一部分能够独立的在句法和语义上同时实现相对于语言总体的功能独立性？

事实上，很多非经典逻辑具有类似的倾向，我们可以笼统的将其概括为“反对形式系统在功能上的整体主义”，它们都有着各自独特的动机，信念修正或许是这方面最具典型性的例子：一个信念状态自身是封闭的，对于信念状态以外的表达式，信念状态具有功能上的独立性。这种独立性摆脱了传统本体论条件句逻辑的本体论包袱，而且贯彻了有限理性的直观思想。

还有些不那么典型的例子，譬如在句法或语义实体之间建立距离关系的各种努力：相干逻辑中，对相干蕴含式前后件在符号上的关联性，潜在的为表达式之间确立了某种距离关系。直陈条件句逻辑，本体论条件句逻辑同样以某种形式建立了表达式与表达式或者可能世界与可能世界之间的距离关系。语言的或语义的实体之间距离关系的建立意味着语言整体具有某种空间分布，这种空间分布决定了至少语言的一部分功能是依赖空间分布上的语言局部而实现的。

另一方面，在涉及到语境或者情境的各种形式系统中，可能世界被按照语境或情境的条件进行了分类，譬如Kaplan的二维语义（[5]），Stalnaker关于预设与语境的工作（[7]）。这种分类的本质是借助那些本体论上被假定为“完整的”可能世界而构造本体论上“不完整的”可能世界，即由那些被筛选出的可能世界的共同特征所决定的世界的局部。

我们看到，各种“反对形式系统在功能上的整体主义”的非经典逻辑，其语义要么依赖于某种针对可能世界的“类型选择”，要么可以被等价的转换为依赖“类型选择”的语义，其中的一部分要求对“类型选择”的方式描述的更加具体，而另一部分则诉诸于“选择函数”，并一直为如何定义“选择函数”而争论。“类型选择”在技术上就是“过滤”。如前所述，Γ相对于子公式的封闭性要求语言的局部只能在命题变元集上被划定。命题变元是彼此独立的，因此可以生成自由的代数结构。但仅就构造过滤而言，这种“自由”是不必要的，因为一个布尔代数可以经由非独立的生成子生成。对于前述种种非经典逻辑而言，“语言的功能局部”的直观背景常常在句法上不涉及对“原子命题”的假设，在语义上相应的，不要求对“可能世界”的描述能够“极大一致”。这样看来，用“子公式封闭集”进行过滤，使得我们常常将过滤的“网眼”画得太细了，不仅限制了系统的功能性，也在说明语义的直观背景时被迫背负沉重的本体论负担。

上述“过滤”方法与直观背景之间呈现出的分裂可以归结为两种可能世界本体论直观之间的冲动：“子公式封闭集”使得“过滤”方法倾向于一种对Abstractionsim（[4]）可能世界的本体论承诺，而“形式系统在功能上的局部主义”则倾向于Combinatorialism（[1,2]）可能世界的本体论承诺。为区别两者，我们可以用一个不太恰当的比喻：如果说世界是一条染色体，那么abstractionism认为世界是事态的模态叠加，即一条染色体上有一系列固定的基因座位，每个基因座位决定了一系列等位基因，因此染色体（可能世界）的种类是每个基因座位上等位基因种类的数量相乘的结果，由基因座位所决定的基因的不同类型直接具有本体论的共同完备性（jointly exhaustive），等位基因之间则是互斥的（mutually exclusive）。而Combinatorialism则认为尽管存在着不同类型的基因，且同类型的基因之间（即等位基因之间）在染色体上互斥，但染色体的长度和顺序是不固定的，即诸类型之间没有共同完备性。所以依靠过滤的方法得到的模型，它会假设可能世界的结构是固定的，可以变换的只是每个“事态座位”上坐着哪个具体的原子事态，这在哲学上符合的是Abstractionism的直观，而“语言功能的局部主义”更加符合Combinatorialism的直观。

从技术上，本文的出发点是提供一种类似于“过滤”但公式集不对命题变元封闭的模型构造方法。在直观背景上本文以及本系列的后续文章的动机是贯彻“功能分布在语言的局部”的主张。即主张一个公式集能够在语言上形成一个局部，使得演绎封闭性被定义在这个语言的局部上，即演绎封闭的公式集只是对相应语言局部上的公式进行二分，而不是对语言上的全体公式。公式集不对命题变元封闭不等于不对“子公式”封闭，只是此时的子公式不只要求在全局语言上“可表征”（representable），如命题变元，而且要求其在局部语言上也是“可表征”的。如何在一个公式集Γ和组成Γ中公式的那些命题变元之间恰当的建立一个语言的局部是技术上的关键。这也使得“局部语言”的技术方法和直观背景在Combinatorialism的可能世界观上得到统一。

2 预备

此部分内容主要整理自文献[3,4]。

基础语言L0是代数类型F0={⊥,¬,∨,∧}在一个以变元（符号）集X上的项集Term0(X)，相应的有项代数Term0(X)=〈Term0(X),F0〉。在后文中，当我们使用L0指Term0(X)，用L0指相应的代数Term0(X)。令Y⊂X，则有基础语言L0的x型局部语言Term0(Y)，即F0在X的子集Y上的项集。相应的有项代数Term0(Y)=〈Term0(Y),F0〉。Sg表示一个代数A=〈A,F0〉上的子域算子，Sg(X)在X⊂A时表示由子集X生成的子域。一个F型代数的类K被称为一个簇（Varieties），如果它在子代数，同态映像，和直积下封闭，记作V(K)=K。我们用Con(A)表示代数A上所有全等关系（Congruences）的集合；用Id(X)表示L0上全体恒定式（Identities）的集合{p≈q:〈p,q〉∈L0×L0}；将双射τ:Id(X)→L0×L0定义为τ(p≈q)=〈p,q〉；用IS(K)表示一个代数类K在子代数同构映像下的闭包；用“⊨”表示代数（类）与恒定式（集）之间的满足关系。

定义1 令B是一族布尔代数，给定变元集X在L0上定义了全等关系θB(X)=∩ΦB(X)，其中ΦB(X)={ϕ∈Con(L0):L0/ϕ∈IS(B)}。则称上相对B自由的布尔代数。

定理1 对于每个A∈B以及每个映射α:X→A，都存在一个同态我们称这个结论为在X上对B的全局映射性，称X为B的一个自由生成子的集合，并称由X自由生成。

定理2 θB=τ(IdB(X))，其中IdB(X)={p≈q∈Id(X):B⊨p≈q}。

定义2 设B是A的子集，θ是A上的全等。则Bθ={a∈A:B∩a/θ≠∅}。令Bθ是A经由Bθ的子代数。同时定义θ↾B为θ∩B2，叫做θ对B的限制。

3 第一类基本结构

注记1 以下，我们将借助L0中的项构造一种代数（局部代数），它处于B之内。尽管此类代数的元素来自L0，但我们不能简单的认为它们是符号，确切的说，它们是作为符号的元素。我们会为局部代数建立一套统一的符号系统，这个系统通过上项的唯一可读性、项所表征的函数以及项与项之间的子项关系为每个项确定了一个二叉树，并通过二叉树上的极大反链建立了子项之间的组合规则。有了这个系统，才有适用于局部代数的等式逻辑。但由于本文的篇幅所限，这部分内容将在后续文章中加以介绍。

通过L0上的元素，有两种最直接的方式来构造新的代数：我们可以依赖于X的子集Y构造也可以用子集Γ⊂L0，用Γ/θB生成子的子代数。前者可以使得每个等价类上项的变元被限制在Y之内，但结构上却是单一的，即如果X和Y具有相同的基数，则与总是同构的，因为Y中的元素是彼此独立的。后者的生成集上的等价类一般不是独立的，但在各等价类上，项的结构仍然依赖于X，因为等价类是在L0上被定义的。

现在，我们可以简单的将两种方式结合在一起，即由Γ⊂L0中出现的全体变元确定一个Y⊂X，再用Y对θB进行限制，即取θB∩(Term0(Y)×Term0(Y))记为θB↾Term0(Y)，这是类似于模态逻辑过滤模型的方法，但是这依然要假定某种Abstractionism式的可能世界，也就是上的超滤。或者也可以直接把Γ上的元素作为生成子，从而把前面的限制条件由Term0(Y)换做Term0(Γ)，但此时Term0(Γ)上很多的项是可以用L0上更简单的项来加以表征的，例如当x1∨(x1∧x2)∈Γ时，如果x1,x2Γ，我们是否应该考虑在x1∨(x1∧x2)∈Γ的子公式x1,x2,(x1∧x2)中选择将x1加入到当前语言的局部中来？另一方面，如果采用Γ上的元素作为当前局部的生成子，那么对于x1∨(x1∧x2)∈Γ，我们一般不会有(x1∧x2)∨x1∈Γ，更不会有x1∨(x2∧x1)∈Γ，(x2∧x1)∨x1∈Γ，这是否是自然的？我们可以在Γ与Y之间建立某种中间的层位作为当前局部的生成子集。

定义3 令公式集Γ⊂L0，令Y⊂X是Γ诸项中所出现的变元的集合。则称Term0(Y)是由Γ生成的x型局部语言，记作xL0(Γ)，相应的有：

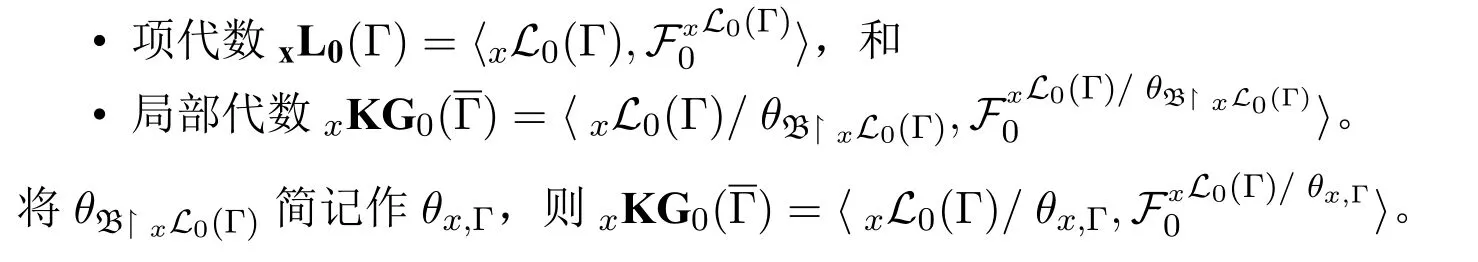
定义4 一个代数A的元素a在其由Γ⊂A生成的子代数B中是可表征的，如果p∈B。

定义5 令A⊂L0，我们称A是L0的局部语言，当且仅当，A是L0的子域，并且对于任意a,b∈xL0(A),〈a,b〉∈θB↾xL0(A)，有若a∈A，则b∈A。

定理3 我们定义L0(Γ)=(Sg(Γ))θx,Γ，则有L0(Γ)是L0的局部语言。（证明略）

4 原始配置

由原始配置，我们可以扩充局部代数上的全等关系，甚至使其退化（Degenerate），但全局上的退化不意味着局部的退化，某个局部上的退化也不意味着其他局部的退化以及退化局部上更细小局部的退化。这也是Combinatorialism与Abstractionism两种直观背景的一个重要差异：前者不假定语言对世界的描述可以是极大一致的，因此语言构造了我们对世界的印象，而后者的世界先于语言存在，语言的功能限于描述世界之间的差异。

定义7 令A是一个代数，Con(A)是A上全体全等关系的集合，则Con(A)是一个代数格。令∇=A×A，令△={〈a,a〉,a∈A}，则∇是Con(A)的全上界，△是Con(A)的全下界。我们定义A×A上的代数封闭算子ϑ，使它恰是用来定义代数格Con(A)的子域封闭算子。

定义8 对于由X生成的全局语言L0，我们为其添加一个项的有序对的集合I∈L0×L0。全局语言L0在获得了原始配置I后，会获得一个新的全等关系以及相应的全局代数

定义9 带原始配置的x型局部代数在由Γ∈L0生成的，x型局部语言xL0(Γ)上，由原始配置I会得到一个新的全等关系以及相应的x型局部代数

注记3 原始配置I在语言局部的作用是具有伸缩性的：局部语言L0(Γ)在I上划定了一个范围，只有当p,q∈L0(Γ)时，〈p,q〉∈I才能够在局部语言L0(Γ)上被表征，但是I中能够被当前局部语言表征的部分会为xL0(Γ)扩充其全等关系，使得L0(Γ)在扩充后的等价类上不再是整齐的，即不满足定义5对局部语言的要求。而当我们对L0(Γ)进行扩充，使它在xL0(Γ)上重新变得整齐以后，就可能有新的I中的序对在新扩充的语言上变得可表征。这个过程循环往复，但这个过程是有极限的，因为局部语言的扩充显然存在一个上界，就是xL0(Γ)本身，而全等关系的扩充同样存在一个上界，就是Θ0,x,I(Γ)。并且明显的，局部语言L0(Γ)受到I的控制，在xL0(Γ)上扩充的每一步，得到的都是xL0(Γ)上的一个整局部。

定义10 受到I控制的局部语言L0,I(Γ)我们借助递归函数L0,I(Γ,n)来定义局部语言L0,I(Γ)如下：

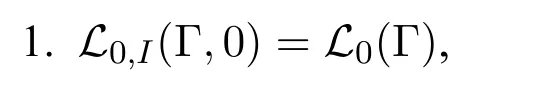
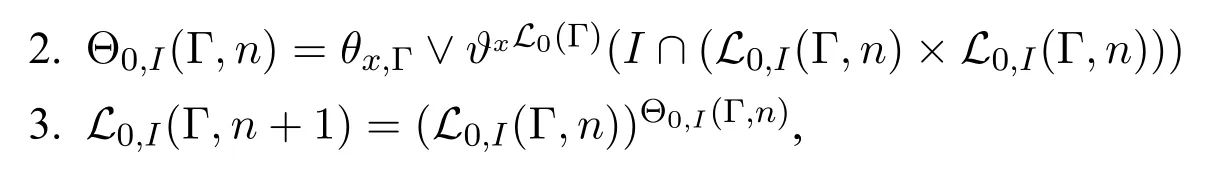
于是，我们定义：

定理4 对于任意n≥0，有Θ0,I(Γ,n)是xL0(Γ)上的全等，且L0,I(Γ,n)是L0的局部语言。（证明略）

注记4 L0,I(Γ,n)是I在xL0(Γ)的范围内对L0(Γ)实施的扩充。其中L0(Γ)的构造依赖于θx,Γ，对L0(Γ)扩充的每一个步骤依赖于对θx,Γ扩充的每一个步骤。我们称L0(Γ,n+1)−L0(Γ,n)是扩充过程产生的语言的层，Θ0,I(Γ,n+ 1)−Θ0,I(Γ,n)是扩充过程中产生的全等的层。我们说L0(Γ,n+1)−L0(Γ,n)这一层诱导了Θ0,I(Γ,n+1)−Θ0,I(Γ,n)这一层。而Θ0,I(Γ,n+1)−Θ0,I(Γ,n)这一层又继而诱导了L0(Γ,n+2)−L0(Γ,n+1)这一层。

定理6 局部封闭定理

一：Θ0,I(Γ)不扩充 L0,I(Γ)，即对应任意 p∈ L0,I(Γ)，有 p/Θ0,I(Γ)⊂L0,I(Γ)。二:L0,I(Γ)不扩充Θ0,I(Γ)，即Θ0,I(Γ)∩I=(L0,I(Γ)×L0,I(Γ))∩I。

证明:一：若p∈Sg(Γ)，则结论明显成立，否则，或者p∈L0(Γ)，或者存在n≥ 0使得p∈L0(Γ,n+1)−L0(Γ,n)。任取q∈p/Θ0,I(Γ)，则〈q,p〉∈Θ0,I(Γ)，则或者〈q,p〉∈0,I(Γ,0)，或者存在m ≥0，使得〈q,p〉∈Θ0,I(Γ,m+1)−Θ0,I(Γ,m)。若n≥m，则自然有q∈L0,I(Γ)；若m＞n，则q∈L0,I(Γ,m+1)。

二：第一步，往证Θ0,I(Γ)∩I⊂(L0,I(Γ)×L0,I(Γ))∩I。任取〈p,q〉∈Θ0,I(Γ)∩I。则要么 〈p,q〉∈ θx,Γ，要么存在 〈p,q〉∈ Θ0,I(Γ,0),要么存在n使得〈p,q〉∈Θ0,I(Γ,n+1)−Θ0,I(Γ,n)。故总是存在L0(Γ,n+1)使得〈p,q〉∈L0(Γ,n+1)×L0(Γ,n+1)∩I。所以有〈p,q〉∈(L0,I(Γ)×L0,I(Γ))∩I。第二步，往证(L0,I(Γ)×L0,I(Γ))∩I⊂Θ0,I(Γ)∩I：任取〈p,q〉∈(L0,I(Γ)×L0,I(Γ))∩I，则总存在n≥0使得p,q∈L0,I(Γ,n)，则有〈p,q〉∈Θ0,I(Γ,n)。

定理7 根据第三同构定理易知，若令Sg(Γ)/(Θ0,I(Γ)↾Sg(Γ))=A，A为以相应的F型代数，则有

5 滤子

在以后的工作中，我们需要在为局部代数建立的符号系统上定义可满足性和演绎后承关系。由于我们的模型是由一个项集Γ⊂L0生成的，因此定义可满足性的前提是明确项集Γ和由其生成的的局部代数之间“满足关系”，确切的说就是在上是否存在一个超滤，使得是这个超滤的子集。更进一步的，如果存在着这样的超滤，那么它是不是唯一的。

定义11 若X⊂B，B是布尔代数，则令¬X={¬a:a∈X}。

定理8([3]，第143页) 对于给定布尔代数B有：对于任意id⊂B，id是理想，当且仅当，¬id是过滤。对于任意fi⊂B，fi是过滤，当且仅当，¬fi是理想。

特发性脊柱侧凸的分型经过长期的研究和探索，随着特发性脊柱侧凸数据库的不断扩大，也伴随着影像设备及技术的不断更新，从单平面到双平面，再到三平面，逐渐向三维发展，从普通的X线平片、普通CT、单层螺旋CT、多层螺旋CT的进步，应用CT的强大的后处理功能，能进行更精细的研究，进一步与特发性脊柱侧凸解剖畸形相贴合，对其畸形的理解更加精确。未来可以对特发性脊柱侧凸应用EOS影像系统进行三维立体数据建模、3D打印建模以及有限元分析，使特发性脊柱侧凸的分型更加准确，从而对该疾病的矫形进行全方位指导。

定理9([3]，第144页) 令B是布尔代数。若θ是B上的二元关系，则θ是B上的全等当且仅当，⊥/θ是一个理想且对任意a,b∈B有:〈a,b〉∈θ iff¬(a↔b)∈⊥/θ。

定理10([3]，第148页) 令B是一个布尔代数，则第一，B上所有理想（ideals）的集合（记作Ideal(B)）在⊂下构成一个分配格。第二，B上所有的过滤（filters）的集合（记作Filter((B))）在⊂下构成一个分配格。第三，上述两个格都与Con B在下述映射下同构：

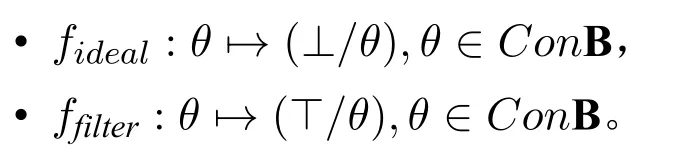
定理11 令代数A∈B，filter∈Filter(A)，则有¬(filter)∪filter是A上的子域。

证明:只需证明A上的任意元素对∧,∨,¬封闭：

任取p∈ filter，则¬p∈ ¬(filter)，于是有¬p∈ filter∪¬(filter)。任取p,q∈filter，自然有p∨q∈filter和p∧q∈filter。（若p,q∈¬(filter)亦然，这是根据过滤和理想的定义）。任取p∈filter，q∈¬(filter)，则有p∨q∈filter，p∧q∈¬(filter)。 □

引理1 A是F型代数，θ∈Con(A)，α:A→A/θ，则有α(Sg(Γ))= Sg(Γ/θ)。进一步的，若将α限制在Sg(Γ)上的部分记为α′，则其是从A的子代数B到A/θ的子代数C的满同态，其中B=Sg(Γ)，C=Sg(Γ/θ)。

引理2 若A是一个代数，Γ∈A，B=Sg(Γ)，θ∈Con(A)，则有B/θ↾B～=C，其中C=Sg(Γ/θ)。

定理12 令Γ∈L0，Sg(Γ)/θB↾Sg(Γ)=A，使得A是F型代数。若有filter∈Filter(A)使得Γ/θB↾Sg(Γ)⊂filter，则有filter是A上的超滤或平凡滤。

证明:令C=Sg(Γ/θB)，则有AC。

定理13 令A是一个布尔代数，θ∈ConA，则对于自然同态α:A→A/θ有对任意A上的超滤ultrafilter有α(ultrafilter)要么是A/θ上的超滤，要么是A/θ。

定理14 令A是一个布尔代数，θ∈ConA，则对于自然同态α:A→A/θ，直接根据过滤的定义和上述结论，我们可以方便的证明以下结论：

1.令filter是A上的过滤，则αfilter是A/θ上的过滤。特别的，α(filter)是超滤，当且仅当，filter∨ffilter(θ)是超滤；α(filter)是平凡滤，当且仅当，是平凡滤，当且仅当，

2.令filter是A/θ上的过滤，则α−1(filter)是A上的过滤。特别的，若filter不是平凡滤，则α(filter)不是平凡滤；若filter不是超滤，则α(filter)不是超滤。

证明:令Γ∈L0。

令Sg(Γ)/θB↾Sg(Γ)=A，A为以相应的F型代数Sg(Γ)/(Θ0,I(Γ)↾Sg(Γ))= B，B为以相应的F型代数，则有：

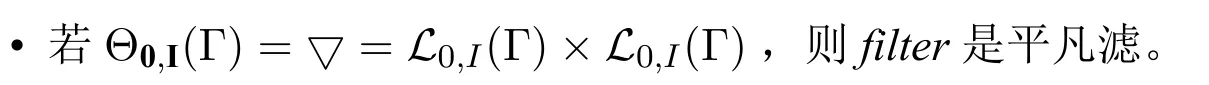
6 第二类结构

在第一类局部结构中，我们需要借助于xL0(Γ)来完成对局部代数的构造，这使得最终L0(Γ)与L0,I(Γ)的生成元素会比我们所期望的要多。譬如对于x1∨(x1∧x2)∈Γ，我们自然会有x1∈L0(Γ)，但同时对于一个任意的xn∈xL0(Γ)，即便xn∉Γ，也会有x1∨(x1∧xn)∈L0(Γ)，尽管此时可能并没有xn∈L0(Γ)。这不能说是一个十分理想的结果，但如果拒绝接受这个结果，我们也会付出相应的代价，譬如对于x1∨(x1∧x2)∈Γ，我们可以令按照下面方法构造的局部语言包含x1，但它一般不会包含(x1∧x2)∨x1，以及x1∨(x2∧x1)。

定义12 令p∈L0，我们用Sub(p)表示p在L0在L0上子项的集合。相应的，我们可以定义L0的β型局部语言如下：

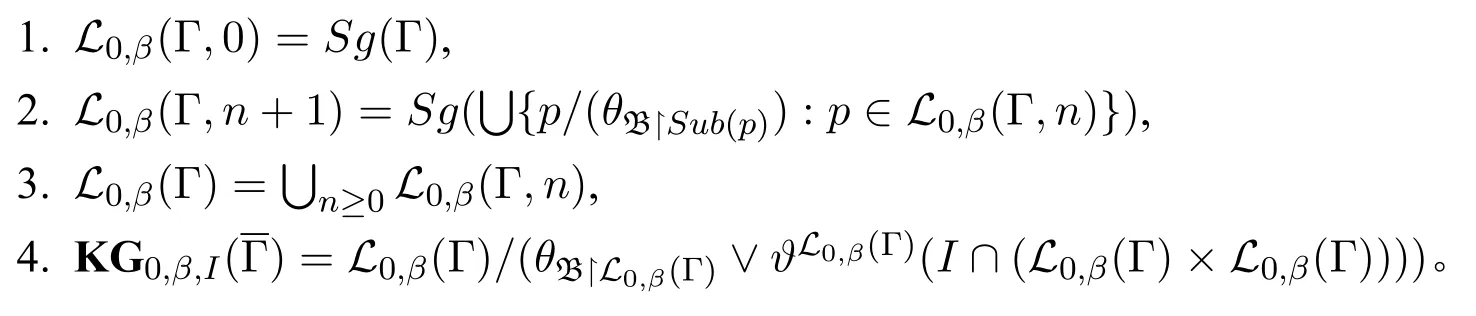
与第一类局部结构不同的是I不扩充L0,β(Γ)。此外所有结论的证明与第一类局部代数相仿，只是需要进行连续扩充的变成了L0,β(Γ)。

此外，还存在着另一种建立局部语言的方法，就是借助于包含参数的L0项可表征函数（我们根据Γ中的项p和其子项q，q∈Γ，可以用p在L0中所表征的函数构造一个包含参数的布尔可表征函数，再用这类函数构造局部语言和局部代数）这类似于布尔代数的相对化（[6]，第38页），但依照此类方法由Γ生成的局部代数，即便不包含原始配置I，也将是与L0/θB由Γ/θB生成的子代数不同构的。由于篇幅所限，对这种结构的讨论将在后续文章中进行。

[1] D.M.Armstrong,1993,“A world of states of affairs”,Philosophical Perspectives,7: 429–440.

[2] D.M.Armstrong,1997,AWorldofStatesofAffairs,Cambridge,NewYork:Cambridge University Press.

[3] S.Burris and H.P.Sankappanavar,1981,A Course in Universal Algebra,Springer.

[4] G.Gratzer,2008,Universal Algebra,New York:Springer.

[5] D.Kaplan,1989,Themes From Kaplan,New York:Oxford University Press.

[6] S.Koppelberg,1989,Handbook of Boolean Algebras Volume 1,New York:Elsevier Science Publishers.

[7] R.Stalnaker,1974,Context and Content,New York:New York University Press.

（责任编辑：罗心澄）

Algebraic Structures of Local Languages—Some General Observations about Local Semantics(1)

Fei Zha
Faculty of Philosophy,Nankai University
zhafei@nankai.edu.cn

B81

A

2016-09-27

中央高校基本科研业务费专项资金资助项目NKZXB1257。

In modal logic,a set of formulas which is used to build filtrations is designed to be closed under subformulas.In fact,such requirement is unnecessary,since a boolean algebracouldalways begeneratedfrom non-independentgenerators.Withthehelp ofsubuniverse generating operator,models of combinatorial possible worlds could be defined, in order to implement D.M.Armstrong’s Combinatorialism,which could be named as“Local Semantics”.It is easy to see that Local Semantics can be applied to the discussion of belief states,linguistic contexts and artificial intelligence in philosophical logic.