邻域语义与修正真理论

林其清

华南师范大学 政治与行政学院

linqiqing@foxmail.com

梁晓龙

中山大学 逻辑与认知研究所

lianghillon@gmail.com

邻域语义与修正真理论

林其清

华南师范大学 政治与行政学院

linqiqing@foxmail.com

梁晓龙

中山大学 逻辑与认知研究所

lianghillon@gmail.com

古普塔和赫兹伯格在1982年各自独立地提出了修正真理论，建立了可用于分析真与相关悖论的修正序列。修正真理论根据语句在所有修正序列中的表现，对语句进行分类。然而，修正真理论在某些语句的分类上不能令人满意，如修正真理论把柯瑞悖论的逆命题断定为绝对地真，这与直觉不一致。本文将从两种路径引入邻域语义研究修正真理论。路径一是在基模型上引入邻域基模型，建立邻域基模型修正序列。这类修正序列比经典修正序列更多，增加的修正序列可使包括柯瑞悖论的逆命题在内的一些语句的病态呈现出来。路径二是通过引入邻域语义模型，使得对任意不含模态词的公式ϕ，模态公式□ϕ在后继阶段的真值可以反映ϕ在上一阶段的真值，并且□ϕ在极限阶段的真值可以反映ϕ在至这个极限阶前是否稳定真。从而可以通过□ϕ的真值来限定T┍ϕ┑的真值，使得满足相应限制的模型类表示了相应的修正序列。本文最后将对两个路径进行整合，构造出能表示邻域基模型修正序列的整体修正序列模型。

修正真理论；修正序列；邻域语义；柯瑞悖论的逆命题

1 修正真理论与关系语义

1.1 修正真理论

塔斯基认为一个合理的（相当于某个）语言的真谓词定义必须蕴含(T)模式的所有代入特例：

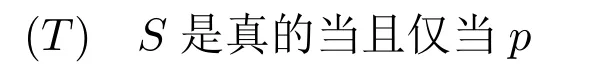
其中p可以代入该语言的任何语句，S是p在该语言中的名称。由于说谎者类型语句的存在，塔斯基认为句法资源丰富的语言无法定义自身真谓词。

古普塔和贝尔纳普认为(T)模式的“当且仅当”不应该看作实质等值，而应该看作是在下定义，(T)模式的每个代入特例都是真谓词的一个部分定义，所有这些部分定义的总体给出了真谓词的完整定义，真谓词是一个循环概念。古普塔和贝尔纳普认为循环概念有其合理性及其运作方式，传统定义理论要求定义项中不能直接或者间接地出现被定义项的要求是不合理的。非循环的定义，如G(x)=dfA(x)，其中A(x)不包含G直接或者间接的出现，这类型的定义提供了一条“绝对”的规则供我们判断一个对象是否属于G的外延：若对象d满足A，那么d就属于G的外延；反之，d不属于G的外延。循环定义并不提供一条绝对的规则，而是提供了一条“修正”的规则。由于循环定义的定义项中包含了被定义项，所以只有先给出被定义项的假设的解释，才可以通过定义来产生被定义项的新的解释，即通过定义“修正”对被定义项的假设的解释，产生被定义项的新的解释，这个新的解释比原来的假设更好。古普塔和贝尔纳普认为我们日常所使用的真谓词就是循环定义的一个特例。他们声称：根据对真谓词的这个看法，真谓词的大部分行为，无论是正常的行为还是病态的行为，都可以得到解释。（[5]，第137页）

若L是由一阶语言L−加入一个特殊的一元谓词符T膨胀所得的一阶语言，并且L−满足对于L中的任意语句φ，┍φ┑都是L−的常元符，那么就把L称为真语言，把L−称为L的基语言，把┍φ┑这样的常元符称为引用常元符，把不是引用常元符的常元符称为非引用常元符。称模型M=〈D,I〉为真语言L的基模型，如果模型M满足以下三个条件：

1.M是基语言L−的经典模型；

2.记L中所有语句的集合为Sent(L)，Sent(L)⊆D；

3.对于任意的φ∈Sent(L)，I(┍φ┑)=φ。

L为一个真语言，M=〈D,I〉是L的基模型，如果h是Sent(L)的一个子集，则把h称为一个假设。如果M′=〈D,I′〉是M相对于L的膨胀模型，并且I′(T)=h，则把M′记为M+h。若M+h⊨φ，则称φ在模型M+h下为真；若M+hφ，则称φ在模型M+h下为假。若φ∈h，则称h把φ断定为真；若φ∉h，则称h把φ断定为假。

给定真语言L，L的基模型M=〈D,I〉，修正规则τM把假设映射到假设，τM规定如下（为简便起见，在不引起混淆的情况下，仅以τ表示τM）：

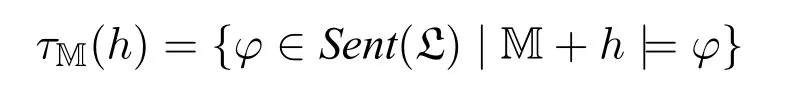
任给T的尝试性的解释，不妨记作h，τ作用在h上产生一个比h更好地作为T的解释的假设τ(h)，τ的再一次作用又可以产生比这个新的解释更好的解释，假设τ(τ(h))，简记为τ2(h)，以此类推可以得到一个ω长的假设序列：τ3(h),τ4(h),τ5(h),···,τn(h),···。为了使修正可以超穷地进行下去，除了修正规则外还需要一个极限规则。有了极限规则后，就能得到以h为初始假设的全序数长的修正序列。

1982年古普塔和赫兹伯格各自独立地提出修正真理论时他们所提出的极限规则是不一样的。同一年，贝尔纳普对他们的极限规则进行批判，并提出了一个更加自由的极限规则。三位作者都同意：在极限阶段之前稳定下来的语句（指从这个极限阶段之前的某个阶段起至这个极限阶段以前一直被断定为真或一直被断定为假的语句）应该被断定为同样的真值。但是他们对至这个极限阶段不稳定的语句（指至这个极限阶段并非稳定的语句）采取了不同的对待。古普塔认为至这个极限阶段不稳定的语句如果在初始假设被断定为真，则这个极限阶段应该把它断定为真，否则应该把它断定为假。把这样的极限规则称作G-极限规则，按照G-极限规则建立起来的修正序列称作G-修正序列。赫兹伯格认为至这个极限阶段不稳定的语句应该一律被断定为假。把这样的极限规则称作H-极限规则，按照H-极限规则建立起来的修正序列称作H-修正序列。贝尔纳普认为至这个极限阶段不稳定的语句可以随意地被断定为真或者被断定为假。把这样的极限规则称作B-极限规则，按照B-极限规则建立起来的修正序列称作B-修正序列。当不指明时，修正序列指B-修正序列。

古普塔在其1982年的论文《真与悖论》（[4]）中提出，给定真语言L和L的基模型M=〈D,I〉，可以根据L中语句在所有修正序列中的表现（“稳定地被断定为真”又简称为“稳定真”；“稳定地被断定为假”又简称为“稳定假）对语句进行分类：

①在所有修正序列中稳定真；

②在所有修正序列中稳定假；

③在某些修正序列中稳定真，在其它修正序列中稳定假；

④在某些修正序列中稳定真，在其它修正序列中不稳定；

⑤在某些修正序列中稳定假，在其它修正序列中不稳定；

⑥在一些修正序列中稳定真，在另一些修正序列中稳定假，在其它修正序列中不稳定；

⑦在所有的修正序列中都不稳定。

修正真理论把第①类语句称为绝对真语句，把第②类语句称为绝对假语句，把其它类型语句合称为病态的语句。③、④、⑤、⑥、⑦这五类语句又相当于是对病态语句的一个划分，反映出存在五种不同类型的病态。

1.2 线性修正序列模型

在修正序列中某一个后继阶段上T谓词的解释决定于该阶段的前继中语句的真假情况。这个规定类似于可能世界语义中对于模态词的解释，熊明于《塔斯基定理与真理论悖论》（[12]）一书中表达过这个思想，他的相对化T模式正是把这一认识推广到了任意的关系框架上得到：

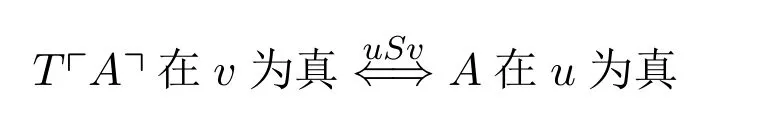
其中：S为给定的通达关系（[12]，第43页）。

受这个认识的启发，我们给出线性序列模型和线性修正序列模型的定义。

定义1(线性序列模型) 给定一个真语言L，称M=〈W,R,D,I,H〉为一个线性序列模型，其中W={wn|n∈ω}为可能世界集（本文中ω指第一个可数无穷序数，也指自然数集），R⊆W×W为可能世界之间的通达关系，且R={(wn+1,wn)|n∈ω}，〈D,I〉为L的基模型，H是一个由W到P(Sent(L))的函数。对任意w∈W，记H(w)为hw。

这个模型实质是在语言L的基础上增加了模态词□所得的语言L□的可能世界语义模型。可看出R的逆关系的传递闭包在W上刚好形成一个序型与(N,＜)一样的严格良基线序。线性序列模型上的R关系图示如下：

定义2(真值条件) 给定可能世界w∈W、任意L□中公式ϕ,ψ及指派σ，为由σ根据〈D,I〉扩展到从L的项的集合到D的函数，线性序列模型的真值条件规定如下：

规定：M,w⊨ϕ，当且仅当，对任意指派σ有M,w⊨σϕ。

定义3(线性修正序列模型) 称M=〈W,R,D,I,H〉为一个线性修正序列模型，如果M为一个线性序列模型，且对于任意n∈ω及L中语句ϕ，M,wn+1⊨T┍ϕ┑当且仅当M,wn+1⊨□ϕ。

在上述定义的线性修正序列模型中，我们要求模型中的可能世界集W 及W上的关系R同构于自然数集及其“减一”运算的结构。这种结构下的线性修正序列模型实际上只能模拟一个ω长的修正序列。但是在修正真理论中，对语句进行区分时，不仅要考虑该语句在一个修正序列中的表现，而且要考虑该语句在所有修正序列中的表现。故我们给出一个新定义，这个定义可以容纳多个甚至全部的ω长的修正序列。

定义4(序列模型) 给定一个真语言L和非空集合WB，称模型M=〈W,R,D,I,H〉为一个序列模型，其中W={wn|w∈WB,n∈ω}为可能世界集，R⊆W×W为可能世界之间的通达关系，R={(wi+1,wi)|w∈WB,i∈ω}，〈D,I〉为L的基模型，H是一个由W到P(Sent(L))的函数。对任意w∈W，记H(w)为hw。序列模型上的真值条件定义方式与定义2相同。

定义5(修正序列模型) 称M=〈W,R,D,I,H〉为一个修正序列模型，如果M为一个序列模型，且对于任意w∈WB、n∈ω及L中语句ϕ，M,wn+1⊨ T┍ϕ┑当且仅当M,wn+1⊨□ϕ。

由定义可知，一个线性（修正）序列模型也是一个（修正）序列模型，此时WB为一个单点集。

若M=〈W,R,D,I,H〉是一个修正序列模型（W={wn|w∈WB,n∈ω}），如果对于任意w∈WB，〈H(wn)〉n∈ω都是一个ω长的修正序列，则称M表示了该组修正序列。

定理1 一个修正序列模型表示了一组ω长的修正序列；给定任意一组ω长的修正序列，可构造一个修正序列模型表示该组修正序列。

证明:给定修正序列模型M=〈W,R,D,I,H〉，其中W={wn|w∈WB,n∈ω}。需证对任意w∈WB及n∈ω，有：H(wn+1)=τ(H(wn))。根据定义，对任意L中语句ϕ：ϕ∈τ(H(wn))，当且仅当〈D,I〉+H(wn)⊨ϕ，当且仅当M,wn⊨ϕ，当且仅当M,wn+1⊨□ϕ，当且仅当M,wn+1⊨T┍ϕ┑，当且仅当ϕ∈H(wn+1)。第一个命题得证。

给定基模型M=〈D,I〉，给定一组ω长的修正序列(Sj)j∈J，J为这组修正序列的标号集。对任意自然数n、任意j∈J，记Sj的第n阶段假设为Sj(n)。存在非空集合WB以及函数f使得f为WB到J上的双射。

构造序列模型M=〈W,R,D,I,H〉，其中W={wn|w∈WB,n∈ω}，R={(wn+1该语句在直观上不应是绝对的语句的观点可参考王文方的文章《古普塔及贝尔纳普的真理修正理论述评》（[11]）。,wn)|w∈WB,n∈ω}，H(wn)=Sf(w)(n)，只需证M为一个修正序列模型。对于任意w∈WB、n∈ω及L中语句ϕ有：M,wn+1|=T┍ϕ┑，当且仅当ϕ∈H(wn+1)，当且仅当ϕ∈Sf(w)(n+1)，当且仅当〈D,I〉+Sf(w)(n)|=ϕ，当且仅当M,wn|=ϕ，当且仅当M,wn+1|=□ϕ。故M为修正序列模型，第二个命题得证。 □

2 邻域语义与修正真理论

经典修正真理论中会把一些直观上认为是病态的语句断定为绝对的语句，例如柯瑞悖论的逆命题：如果说谎者语句φ是真的，那么这句话是真的。1该语句在直观上不应是绝对的语句的观点可参考王文方的文章《古普塔及贝尔纳普的真理修正理论述评》（[11]）。我们认为这类病态语句之所以被断定为绝对的语句，是因为在经典修正真理论中修正序列不够多。我们发现，当在基模型基础之上引入邻域语义模型时，修正序列的数量会大大地增多，这些增加的修正序列能够让这类型语句的病态呈现出来。2引入规范的非经典的赋值模式来建立修正真理论也能使得修正序列数量增多，具体可参考林其清、熊明的文章《克林强三值模式与修正过程》（[10]）。但引入邻域语义基模型的方法可以在保持经典赋值模式的同时增加修正序列数量。

根据前文分析可知，任意一个ω长的经典修正序列，都能相应地被一个满足“对于任意n∈ω及L中语句ϕ，M,wn+1|=T┍ϕ┑当且仅当M,wn+1|=□ϕ”的关系语义模型表示。当我们想要把类似的结论推广到超穷长的修正序列时，我们发现，用（仅有一个模态词的）关系语义模型行不通。于是，我们从另一种路径引入邻域语义模型，通过对极限阶段的可能世界的邻域进行规定，使得□ϕ在极限阶段的真值能反映出ϕ是否在该阶段前稳定真，从而使得类似的结论可以推广到超穷长的修正序列。

2.1 基于邻域基模型的修正序列

首先我们在基模型的基础上引入邻域基模型。由于我们仅关心对T谓词的修正，我们假设在各个可能世界上的论域一样，并且各个可能世界上对L中除T外的部分的解释也一样。

定义6(固定论域邻域框架和固定论域邻域模型3固定论域邻域模型（Constant Domain Neighborhood Model）的定义可参考帕克特的介绍邻域语义的教材（[8]）。) 给定一个语言L，称F=〈W,N,D〉为一个固定论域邻域框架，如果W是一个非空的可能世界集，N为从W到P(P(W))的函数，D为一个集合。称N为邻域函数，称D为论域。称M=〈F,V〉=〈W,N,D,V〉为一个固定论域邻域模型，如果V为一个赋值函数，且对任意w∈W，〈D,V(w)〉为语言L的模型。也称M为基于固定论域邻域框架F上的固定论域邻域模型。

定义7(固定论域邻域模型的真值条件)（[8]）给定可能世界w∈W、任意L□中公式ϕ,ψ及任意指派σ，w为由σ根据〈D,V(w)〉扩展到L的项的集合到D的函数，固定论域邻域模型的真值条件规定如下：

定义8(邻域基模型和邻域假设) 设〈D,I〉为语言L的一个基模型，称固定论域邻域模型M=〈W,N,D,V〉为基于〈D,I〉的一个邻域基模型，如果对任意w∈W，V(w)=I。称函数H:W→P(Sent(L))是邻域基模型M上的一个邻域假设，对于任意w∈W，记H(w)为hw。若M′=〈W,N,D,V′〉，且对于任意w∈W有〈D,V′(w)〉=〈D,I〉+H(w)，则把M′记作M+H。

在经典的修正真理论中，是在基模型的基础上对谓词T的一个假设进行修正，而在本文中，我们在邻域基模型的基础上同时对所有可能世界上的假设进行修正。我们规定一个作用在邻域假设集HM上的修正规则δM，其中HM为邻域基模型M上所有邻域假设构成的集合。为简便起见，在不引起混淆的情况下，仅以δ表示δM。

定义9(修正规则) 给定邻域基模型M，及任意的邻域假设H，规定δ(H)如下：对任意L中语句ϕ，ϕ∈δ(H)(w)，当且仅当，{v∈W|M+H,v⊨ ϕ}∈N(w)。

根据上述定义以及邻域语义中的模态词真值条件可知，对于任意一个邻域基模型M，邻域假设H，可能世界w∈W，及任意L中语句ϕ：M+H,w⊨□ϕ，当且仅当模型M+H中ϕ为真的可能世界形成的集合是w的一个邻域，当且仅当ϕ∈δ(H)(w)，当且仅当M+δ(H),w⊨T┍ϕ┑。

定义10(邻域基模型修正序列) 称一个邻域假设的序列〈Hγ〉γ∈ON为一个全序数长的基于邻域基模型M的修正序列，如果对于任意序数γ∈ON，有Hγ+1=δ(Hγ)；若γ是极限序数，对于任意L中语句ϕ及M中可能世界w，若ϕ在〈Hβ(w)〉β∈γ中稳定地被断定为真，则ϕ∈Hγ(w)；若ϕ在〈Hβ(w)〉β∈γ中稳定地被断定为假，则ϕ∉Hγ(w)。

在不引起混淆的情况下，一个邻域基模型修正序列也被简称为一个修正序列。若〈Hγ〉γ∈ON为一个修正序列，我们也把〈Hγ(w)〉γ∈ON称为一个修正序列。类似地，我们可以定义出α长的修正序列〈Hγ〉γ∈α和〈Hγ(w)〉γ∈α。若邻域基模型M基于基模型M，我们也把基于M的邻域基模型修正序列称为基于M的邻域基模型修正序列。

定理2 任意一组全序数长的经典修正序列，可以用一个全序数长的邻域基模型修正序列表示；类似地，给定非零序数α，任意一组α长的经典修正序列，可以用一个α长的邻域基模型修正序列表示。

证明:给定基模型为〈D,I〉的一组修正序列(Sj)j∈J，J为这组修正序列的标号集。记任一修正序列Sj的第γ阶段假设为Sj(γ)，γ为任意序数。构造基于〈D,I〉的邻域基模型M=〈W,N,D,V〉，其中W={wj|j∈J}，N(w)={A∈P(W)|w∈A}，构造序列〈Hγ〉γ∈ON，使得Hγ(wj)=Sj(γ)。需证〈Hγ〉γ∈ON为基于M的修正序列。

极限阶段的要求可直接通过定义得到。对于任意L中语句ϕ，对于任意序数γ：ϕ∈Hγ+1(wj)，当且仅当ϕ∈Sj(γ+1)，当且仅当〈D,I〉+Sj(γ)⊨ϕ，当且仅当〈D,I〉+Hγ(wj)⊨ϕ，当且仅当{v∈W|M+Hγ,v⊨ϕ}∈N(wj)，当且仅当ϕ∈δ(Hγ)(wj)。故定理的第一部分得证。

类似地，可证得定理的第二部分。 □

定理3 任意一组基于基模型M的全序数长的邻域基模型修正序列，可以用一个基于M的邻域基模型修正序列表示；类似地，给定非零序数α，任意一组基于M的α长的邻域基模型修正序列，可以用一个基于M的α长的邻域基模型修正序列表示。

证明:类似于定理2的证明，仅需对这组序列中的邻域基模型进行不交并操作。 □

给定语言L，基模型M=〈D,I〉，基于M的邻域基模型有很多，考虑一个语句的表现时，不应考虑所有基于M的邻域基模型。因为如果基于M的某个邻域基模型M=〈W,N,D,V〉上的某个可能世界w的其中一个邻域为空集，那么无论我们以任意邻域假设H0作为初始假设构建的任意修正序列〈Hγ〉γ∈ON，L中的逻辑矛盾式（例如φ∧¬φ，φ为L中语句）都会在序列〈Hγ(w)〉γ∈ON上稳定地被断定为真。这不是我们想要的结果，所以我们要求M中不存在这样的可能世界。假设我们期望L中的逻辑有效式（例如φ∨¬φ，φ为L中语句）在我们考虑的修正序列上都稳定地被断定为真，那么必须要求W为所有可能世界的一个邻域，即对任意w∈W，有W∈N(w)。除此之外，对任意邻域假设H，任意可能世界w，若想使得δ(H)(w)为一个一致的假设，可要求N(w)满足有穷交非空的性质。

定义11(MM) 任给基模型M，定义基于M的邻域基模型的类MM如下：任给基于M的邻域基模型M=〈W,N,D,V〉，M在模型类MM中，当且仅当对任意w∈W有W∈N(w)且N(w)满足有穷交非空性质。

推论1 任意一组全序数长的基于基模型M的经典修正序列，可以用一个基于MM中的邻域基模型的修正序列表示；任意一组基于MM中的邻域基模型的修正序列，可以用一个基于MM中的邻域基模型的修正序列表示。类似地，任给非零序数α：任意一组基于基模型M的α长的经典修正序列，可以用一个基于MM中的邻域基模型的α长的修正序列表示；任意一组基于MM中的邻域基模型的α长的修正序列，可以用一个基于MM中的邻域基模型的α长的修正序列表示。

定义12(绝对真/绝对假/病态语句) 给定真语言L，基模型M=〈D,I〉及L中语句ϕ，若对任意M∈MM，任意基于M的修正序列〈Hγ〉γ∈ON，任意M中可能世界w，ϕ都在〈Hγ(w)〉γ∈ON中稳定地被断定为真，则称ϕ是绝对真的语句；若对任意M∈MM，任意基于M的修正序列〈Hγ〉γ∈ON，任意M中可能世界w，ϕ都在〈Hγ(w)〉γ∈ON中稳定地被断定为假，则称ϕ是绝对假的语句；否则，称ϕ是病态的语句。

若L中含有常元符g，容易验证g=g，T┍g=g┑，……这些直观上真的语句都是绝对真的，而g≠g，T┍g≠g┑，……这些直观上假的语句则都是绝对假的。L中的逻辑有效式都是绝对真的；L中的逻辑矛盾式都是绝对假的。根据推论1可知，这里分析一个语句的表现所考虑的修正序列比经典修正真理论所考虑的修正序列更多，经典修正序列构成的类是这里所考虑的修正序列构成的类的真子类。故这个定义下绝对真的语句，也是经典修正真理论中的绝对真的语句；这个定义下绝对假的语句，也是经典修正真理论中的绝对假的语句。

例1(柯瑞悖论的逆命题) L是含有两个非引用常元符a,b的真语言。〈D,I〉为真语言L的基模型，且I(a)=¬Ta，I(b)=Ta→Tb。考虑语句Ta→Tb。在经典的修正真理论中，语句Ta→Tb在任意修正序列中均稳定真，故经典的修正真理论断定Ta→Tb为绝对真。

我们构造如下的邻域基模型：M=〈W,N,D,V〉，其中W={u,v,w,z}；N(u)={{u},{u,w},W}，H0(u)={I(a)}；N(v)={{v},{v,z},W}，H0(v)=∅；N(w)={{u,w},{v,w},{u,w,z},W}，H0(w)={I(a),I(b)}；N(z)= {{u,z},{v,z},{v,w,z},W}，H0(z)=∅。

以H0为初始邻域假设构造修正序列，在每个极限阶段，在任意可能世界上，对至该极限阶段不稳定的语句的断定均与初始阶段相同。所得的修正序列如下：

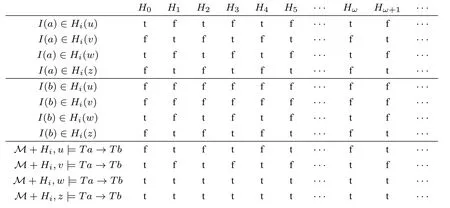
语句Ta→Tb在修正序列〈Hγ(u)〉γ∈ON和修正序列〈Hγ(v)〉γ∈ON中稳定假；在修正序列〈Hγ(w)〉γ∈ON和修正序列〈Hγ(z)〉γ∈ON中不稳定。由此我们看出柯瑞悖论的逆命题不是绝对真的语句，而是一个病态的语句。

库克在[2]中提出了一组语句S1-S4，这组语句有唯一一组一致的真值指派，但经典修正真理论中这些语句都属于病态的语句。因此库克认为这组语句说明了“古普塔和贝尔纳普的修正真理论在捕捉直观上的真概念上并不如我们想的那么成功。”（[2]，第22页）同年，克莱默在[7]中对库克提出的反例进行了回应。他认为S1-S4虽然有唯一一组一致真值指派，但却是病态的。克莱默分析了这些语句病态的原因，同时也解释了为什么这组语句能有一致真值指派。因此，克莱默认为“修正真理论把库克的四个语句S1-S4看作是病态的而不是悖论的语句是正确的，而存在唯一一组与塔斯基条件句一致的真值指派只是这些语句的病态性恰好能够相互取消的副产品。”（[7]，第336页）之后，库克在[3]中提出了另一组语句这组语句同样具有克莱默分析S1-S4时所指出的病态，但在修正真理论中却属于绝对的语句。所以库克认为，克莱默所认为的S1-S4是病态语句的理由不充分。因而库克得出结论“修正真理论的拥护者仍然欠我们一个关于是什么使得S1-S4是病态语句的解释，并且该解释须与有确定真值的事实相一致。”（[3]，第261页）

我们构造如下的邻域基模型：M=〈W,N,D,V〉，其中W={u,v,w,z}；N(u)={{u},{u,v,z},W}，H0(u)={I(b)}；N(v)={{v},{v,w,z},W}，H0(v)={I(a)}；N(w)={{w},{u,w,z},W}，H0(w)=∅；N(z)={A∈P(W)|z∈A}，H0(z)={I(a)}。

以H0为初始邻域假设构造修正序列，在每个极限阶段，在任意可能世界上，对至该极限阶段不稳定的语句的断定均与初始阶段相同。所得的修正序列如下：

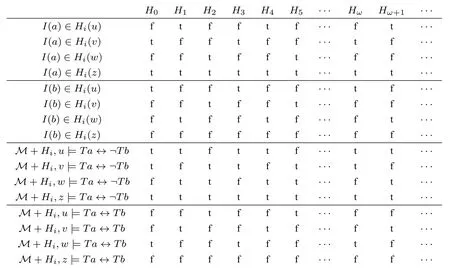
语句Ta↔¬Tb和语句Ta↔Tb，在修正序列〈Hγ(u)〉γ∈ON、〈Hγ(v)〉γ∈ON和修正序列〈Hγ(w)〉γ∈ON中均不稳定。由此我们看出这组语句不是绝对的语句，而是病态的语句。

这个结论支持了库克的观点，修正真理论在真概念的描述问题上并不如我们所想的那么成功；也支持了克莱默所提出的断定语句为病态语句的标准。

类似于前文序列模型和修正序列模型的定义，我们可以给出相应的定义用以表示ω长的邻域基模型修正序列。

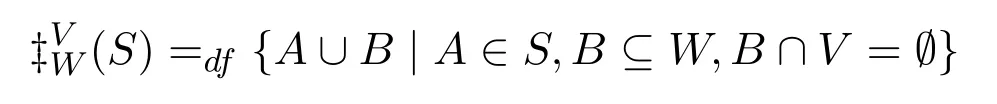
定义函数‡W:P(P(W))→P(P(W))，使得对任意S⊆P(W)，

对于任意集合A及元素w∈A，任意序数集B及序数β∈B，以下列记号简记相应的集合：[A]β=df{vβ|v∈A}；w[B]=df{wα|α∈B}；[A][B]=df{wα|w∈A,α∈B}。

定义13(邻域基序列模型) 给定一个真语言L，给定一个基于〈D,I〉的邻域基模型M=〈W,N,D,V〉及M上的邻域假设H，称N=M+H为一个邻域基序列模型，如果存在基于〈D,I〉的邻域基模型〈WB,N0,D,VB〉，使得：

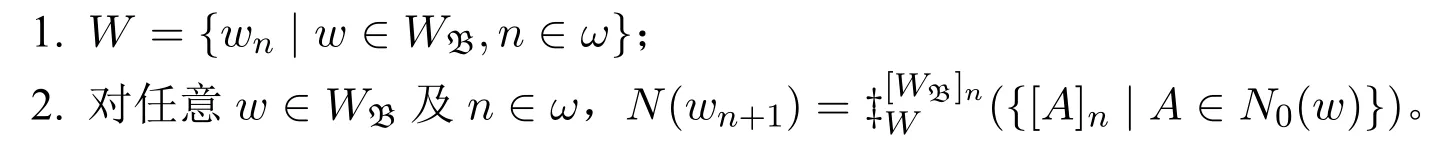
也称N为基于邻域基模型〈WB,N0,D,VB〉的邻域基序列模型。

定义14(邻域基修正序列模型) 称邻域基序列模型N=〈W,N,D,V〉+ H为一个邻域基修正序列模型，如果对于任意n∈ω,w∈WB及任意L中语句ϕ有：N,wn+1⊨T┍ϕ┑当且仅当N,wn+1⊨□ϕ。

若N=〈W,N,D,V〉+H为一个基于邻域基模型〈WB,N0,D,VB〉的邻域基修正序列模型，对于任意n∈ω，定义函数Hn:WB→P(Sent(L))，使得对任意w∈WB：Hn(w)=H(wn)。如果〈Hn〉n∈ω是一个基于〈WB,N0,D,VB〉的ω长的修正序列，则称N表示了这个修正序列。

定理4 一个邻域基修正序列模型表示了一个ω长的邻域基模型修正序列；给定一个ω长的邻域基模型修正序列，可以构造一个邻域基修正序列模型表示该修正序列。

若M=〈W,R,D,I,H〉是一个基于〈D,I〉的序列模型，N=〈W,N,D,V〉+H是基于〈D,I〉的邻域基序列模型。若对任意指派σ、任意w∈W及任意L□中公式ϕ，有M,w⊨σϕ当且仅当N,w⊨σϕ，则称N表示了M。

定理5 所有的序列模型均能被一个邻域基序列模型表示；特别地，所有的修正序列模型均能被一个邻域基修正序列模型表示。

证明:给定任意序列模型M=〈W,R,D,I,H〉，其中W={wn|w∈WB,n∈ω}。

构造邻域基序列模型N=〈W,N,D,V〉+H，其中〈WB,N0,D,VB〉为基于〈D,I〉的邻域基模型，对任意w∈WB，N0(w)={A∈P(WB)|w∈A}，且对任意n∈ω有，(wn+1,v)∈R⇒v∈B}。由关系语义与邻域语义之间的关系可知，对任意指派σ和任意L□中公式ϕ，有M,w⊨σϕ当且仅当N,w⊨σϕ。特别地，根据定义，若M为修正序列模型，则N为邻域基修正序列模型。 □

2.2 不同种类修正序列对应的模型类

我们希望在定义3的基础上增加表示ω阶段的可能世界wω。在线性修正序列模型的定义中，由于wn+1的唯一后继是wn，故对任意L中语句ϕ，ϕ在wn上为真当且仅当□ϕ在wn+1上为真。□ϕ在n+1阶段上的真值恰好反映出ϕ在n阶段的真值，所以可以通过□ϕ在n+1阶段的真值来规定n+1阶段T的外延。但在关系语义中，（仅有一个模态词时）一个可能世界仅拥有一个唯一的后继集，在经典的修正序列中，语句在极限阶段是否属于T谓词的外延取决于语句的“稳定性”（我们暂时考虑赫兹伯格的H-极限规则，即极限阶段T谓词的外延仅包含稳定真的语句）。在ω阶段，无论是W={wn|n∈ω+1}的哪个子集作为wω的后继，都无法使得“对任意L中语句ϕ，□ϕ在wω上为真当且仅当ϕ至ω阶段之前稳定真”成立。而引入邻域语义则可以很好地解决这个问题。不妨令A为所有ω的“ω余有界”的子集（一个ω的子集是ω余有界，是指其在ω中的补集是在ω中有界的），即A={A∈P(ω)|sup(ω−A)＜ω}（对任意一个序数集B，sup(B)为：在全序数构成的类ON中，在严格偏序“＜”下，序数集B的上确界）。令wω的邻域集合为N(wω)=‡W{w[A]|A∈A}。对任意L中语句ϕ，□ϕ在wω上为真，当且仅当，存在A∈A使得ϕ在w[A]上均为真，由于A∈A是ω余有界的，所以当且仅当ϕ在ω阶段前稳定真。故□ϕ在wω上的真值可以反映ϕ是否至ω阶段前稳定真。同理，□¬ϕ在wω上的真值可以反映ϕ是否至ω阶段前稳定假，即：□¬ϕ在wω上为真当且仅当ϕ至ω阶段前稳定假。对任意自然数n＞0，为了使得□ϕ在n阶段的真值可以反映ϕ在n−1阶段的真值，须把N(wn)规定为由{wn−1}生成的主超滤，而‡W({w[A]|A⊆n,sup(n−A)＜n})恰好是由{wn−1}生成的主超滤，故令N(wn)=‡W({w[A]|A⊆n,sup(n−A)＜n})。有了这些规定，我们就可以通过在一个阶段（对应的可能世界）中□ϕ的真值来规定T在该阶段（对应的可能世界）的外延，从而使得满足这些限制条件的模型可以刻画一个相应的ω+1长的修正序列。这种规定可以推广到任意超穷序数α上。

定义15(邻域序列模型)给定基于〈D,I〉的邻域基模型M=〈W,N,D,V〉及邻域假设H，称N=M+H为基于〈D,I〉的一个α长的邻域序列模型（α＞0），如果：

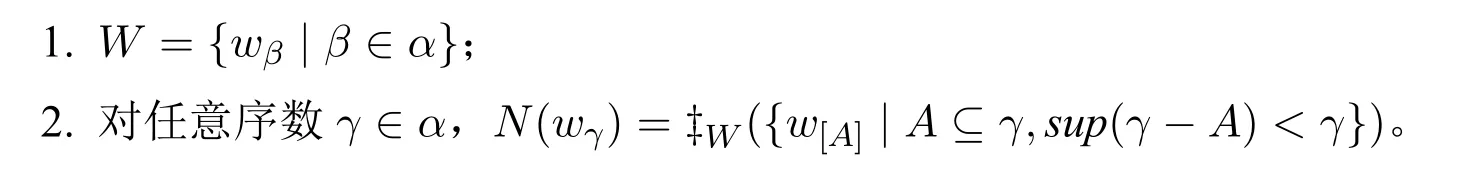
在邻域序列模型中：对于任意0＜γ∈α的可能世界wγ，N(wγ)是W 上的一个滤子；当γ为一个后继序数时，N(wγ)是一个由{wγ−1}生成的主超滤，并且是扩张的。

定义16(H-修正序列模型) 称α长的邻域序列模型N=〈W,N,D,V〉+ H为一个α长的H-修正序列模型，如果对任意0＜γ∈α，任意L中语句ϕ有：N,wγ⊨T┍ϕ┑当且仅当N,wγ⊨□ϕ。

定理6 任给非零序数α，任意α长的H-修正序列模型均表示一个α长的H-修正序列；任给一个α长的H-修正序列，可以构造一个α长的H-修正序列模型表示它。

证明:给定α长的H-修正序列模型N=〈W,N,D,V〉+H，根据N的定义，对任意β+1∈α，τ(H(wβ))=H(wβ+1)；对任意极限序数β∈α，ϕ∈H(wβ)当且仅当ϕ至β阶段前稳定真。对任意β∈α，令hβ=H(wβ)，则〈hγ〉γ∈α为α长的H-修正序列。

给定α长的H-修正序列〈hγ〉γ∈α，可以构造α长的邻域序列模型N=〈W,N,D,V〉+H，使得对任意β∈α，H(wβ)=hβ。需证N为α长的H-修正序列模型。

对任意β+1∈α，任意L中语句ϕ：N,wβ+1⊨T┍ϕ┑，当且仅当ϕ∈hβ+1，当且仅当〈D,I〉+hβ⊨ϕ，当且仅当N,wβ⊨ϕ，当且仅当N,wβ+1⊨□ϕ。对任意极限序数β∈α，任意L中语句ϕ：N,wβ⊨T┍ϕ┑，当且仅当ϕ∈hβ，当且仅当ϕ至β阶段前稳定真，当且仅当{v∈W|M,v⊨ϕ}∈N(wβ)，当且仅当N,wβ⊨□ϕ。故N为一个α长的H-修正序列模型。 □

我们可以把一些固定论域邻域框架上的一些结论，用于分析H-修正序列模型及后文将要定义的各种修正序列模型中语句的表现。首先我们引用如下的一些关于固定论域邻域框架的结论。

定理7 给定任意固定论域邻域框架F=〈W,N,D〉及任意可能世界w∈W，有：

•F满足RE规则：φ↔ϕ⇒□φ↔□ϕ；

•N(w)向上封闭，当且仅当，(F,w)满足公理模式M：□(φ∧ψ)→(□φ∧□ψ)；

•N(w)有穷交封闭，当且仅当，(F,w)满足公理模式C：(□φ∧□ψ)→□(φ∧ψ)；

•W∈N(w)，当且仅当，(F,w)满足公理N：□⊤；

•N(w)为一个W上的滤子，当且仅当，(F,w)满足公理系统K（即EMCN）；

•若N(w)是扩张的（滤子且任意交封闭），则(F,w)满足公理模式BF：∀x□φ(x)→□∀xφ(x)。

证明:具体证明可参考帕克特的介绍邻域语义的教材（[8]）。 □

给定一个α长的H-邻域序列模型N，可知：对任意后继序数β∈α，N(wβ)都是扩张的，所以K+BF系统中的定理在这些可能世界上均为真；而对于极限序数β∈α，N(wβ)不再是扩张的而只是滤子，所以只能保证K系统中的定理在其上为真。

例3(H-修正序列模型ω阶段不满足公理模式BF的例子) L为包含一元谓词符P、二元谓词符Q、常元符、一元函数符s的真语言。归纳定义如下：对任意自然数n，归纳定义如下：对任意自然数m,n，若n=m+1＞1，则。L的基模型〈D,I〉满足I(s)|ω为ω上的后继函数。可知〈I(P),I(s)〉为皮亚诺算术的一个标准模型。令ψ(x)=df∃y(Q(x,y)∧T(y))，φ(x)=dfP(x)→ψ(x)，现考虑公式：∀x□φ(x)→□∀xφ(x)。

考虑基于〈D,I〉的ω+1长的H-修正序列模型N，其中H(w0)=∅。容易验证，对于任意两个自然数i,j，当且仅当i＜j，所以对于任意自然数i，故对任意指派σ，有N,wω⊨σ□φ(x)。但是，对任意自然数j，∀xφ(x)H(wj)，所以N,wω□∀xφ(x)，因而N,wω∀x□φ(x)→□∀xφ(x)。故存在ω阶段不满足公理模式BF的H-修正序列模型。

若对定义16中的邻域函数或者□与真谓词T之间的关系进行调整，我们可以定义出用以表示不同类型修正序列的不同的模型类。

一个B-修正序列是一个MCS-修正序列，当且仅当，该序列在任意阶段的假设均为真语言L的极大一致语句集。

定义17(MCS-修正序列模型) 称固定论域邻域模型N=〈W,N,D,V〉+ H为一个α长的MCS-修正序列模型，如果存在一个α长的邻域序列模型N′=〈W,N′,D,V〉+H，使得，H(w0)为真语言L的极大一致语句集，且对任意0＜γ∈α，任意L中语句ϕ有：

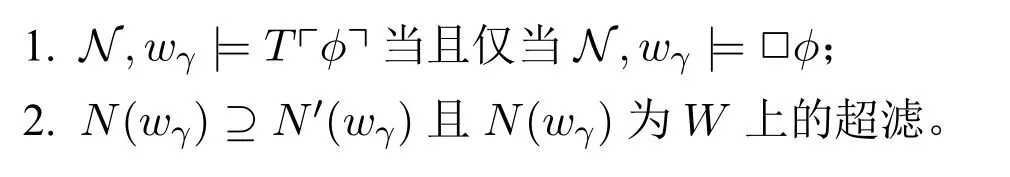
因为任意一个滤子可以扩张成一个超滤，所以该定义是一个良定义。

定理8 任给非零序数α，任意α长的MCS-修正序列模型均表示一个α长的MCS-修正序列；任给一个α长的MCS-修正序列，可以构造一个α长的MCS-修正序列模型表示它。

证明:给定α长的MCS-修正序列模型N=〈W,N,D,V〉+H，根据N的定义，对任意0＜β∈α，N(wβ)是W上的超滤，故H(wβ)为L的极大一致集。若β=γ+1∈α，则由定义可得τ(H(wγ))=H(wβ)；若β为极限序数且β∈α，显然H(wβ)包含所有至β阶段前稳定真的语句，并且，对任意H(wβ)中语句ϕ有：ϕ至β阶段前并非稳定假（若ϕ至β阶段前稳定假，则¬ϕ至β阶段前稳定真，因而¬ϕ∈H(wβ)，这与H(wβ)为极大一致集矛盾）。令hβ=H(wβ)，则〈hγ〉γ∈α为α长的MCS-修正序列。

给定α长的MCS-修正序列〈hγ〉γ∈α，构造α长的邻域序列模型N′=〈W,N′,D,V〉+H，使得对于任意β∈α，H(wβ)=hβ，然后构造固定论域邻域模型N=〈W,N,D,V〉+H，使得：

1.对任意后继序数β∈α，N(wβ)=N′(wβ)，显然N(wβ)为W上的超滤；

2.对任意极限序数β∈α，N(wβ)为W上的超滤，满足：N(wγ)⊇N′(wγ)，且对任意hβ中语句ϕ，{wγ|N,wγ⊨ϕ}∈N(wβ)。

需证，对任意极限序数β∈α，条件2中的超滤N(wβ)存在，且N为α长的MCS-修正序列模型。考虑集合A=N′(wγ)∪{{wγ|N,wγ⊨ϕ}|ϕ∈hβ}。由于hβ为极大一致集，且hβ中的语句都不会至β阶段前稳定假，所以集合A满足有穷交非空性质。故存在满足条件的超滤(wβ)。

证明N为α长的MCS-修正序列模型时，后继阶段的情况与定理6的证明类似。对于极限序数β∈α，对任意L中语句ϕ，显然N,wβ⊨T┍ϕ┑⇒N,wβ□ϕ。另一方面，N,wβT┍ϕ┑⇒ϕhβ⇒¬ϕ∈hβ⇒N,wβ⊨□¬ϕ⇒N,wβ□ϕ。故N为α长的MCS-修正序列模型。 □

定义18(B-修正序列模型) 称α长的邻域序列模型N=〈W,N,D,V〉+ H为一个α长的B-修正序列模型，如果对任意γ∈α，任意L中语句ϕ有：

1.若N,wγ⊨□ϕ，则N,wγ⊨T┍ϕ┑；

2.若N,wγ⊨□¬ϕ，则N,wγ⊨¬T┍ϕ┑。

对于N,wγ/□ϕ且N,wγ□¬ϕ的情况，B-修正序列模型并不要求ϕ是否属于wγ上T谓词的外延。

定理9 任给非零序数α，任意α长的B-修正序列模型均表示一个α长的B-修正序列；任给一个α长的B-修正序列，可以构造一个α长的B-修正序列模型表示它。

证明:证明过程与定理6的证明类似。 □

在α长的B-修正序列模型中，不再满足“对任意序数0＜γ∈α及L中语句ϕ，N,wγT┍ϕ┑当且仅当N,wγ□ϕ”这个限制，为方便起见，后文将把这个限制称为“□～T”限制。如果保留该限制，那么可以通过放宽对邻域函数N的要求，以获得一些其他类型的模型。下面按照这个思路给出E-修正序列模型的定义。

定义19(E-修正序列模型) 称固定论域邻域模型N=〈W,N,D,V〉+H为一个α长的E-修正序列模型，如果存在一个α长的邻域序列模型N′=〈W,N′,D,V〉+H，使得，对任意0＜γ∈α，任意L中语句ϕ有：

E-修正序列模型在保留了“□～T”限制的情况下放宽了对邻域函数N的要求。我们把一个α长的E-修正序列模型对应的α长的序列〈hwγ〉γ∈α称为一个α长的E-修正序列。在E-修正序列模型的定义中，N′(wγ)⊆N(wγ)可以保证在E-修正序列中：至一个极限阶段之前稳定地被断定为真的语句一定在该阶段的T谓词的外延中。而N(wγ)⊆‡W({w[A]|A⊆γ,sup(A)+1≥γ})则保证了：至一个极限阶段之前稳定地被断定为假的语句一定不在该阶段的T谓词的外延中；对于后继阶段，一个L中语句在该阶段的T的外延中，当且仅当该语句在该阶段的前继阶段为真。整体而言，条件2保证了任意一个E-修正序列均是一个B-修正序列。

相比B-修正序列，E-修正序列在极限阶段增加了一个额外要求：对任意L中语句φ,ψ，如果这两个语句在经典逻辑中等价，那么在极限阶段中对这两个语句的真假断定必须相同。B-修正序列并不需要满足这个要求，所以上文模拟B-修正序列时需要放宽“□～T”限制。

需注意，在α长的E-修正序列模型中，当γ∈α为极限序数时，N(wγ)不一定是滤子，所以无法保证wγ满足系统K系统中的定理。

例4(E-修正序列模型ω阶段不满足公理模式C的例子) L为包含常元符a,b的真语言。L的基模型〈D,I〉满足：I(a)=¬Ta，I(b)=Ta。现考虑语句：(□¬Ta∧□Ta)→□(¬Ta∧Ta)。

考虑ω+1长的E-修正序列模型N，其中H(w0)={I(a),I(b)}，N(wω)=‡W({w[A]|A⊆ω,sup(A)=ω})。容易验证，对任意自然数i＞0，I(a)∈H(wi)当且仅当I(a)∉H(wi+1)当且仅当I(b)∈H(wi+1)，进而可得N,wω⊨□¬Ta且N,wω⊨□Ta。另一方面，对任意自然数i＞0，¬Ta∧Ta∉H(wi)，所以N,wω□(¬Ta∧Ta)。从而有N,wω/(□¬Ta∧□Ta)→□(¬Ta∧Ta)。故存在ω阶段不满足公理模式C的E-修正序列模型。

值得注意的是，在E-修正序列模型N的ω阶段中，形如(T┍φ┑∧T┍ψ┑)→T┍φ∧ψ┑的语句不一定为真，即在ω阶段时T的外延并不对合取封闭。

例5(E-修正序列模型ω阶段不满足公理模式M的例子) L为包含常元符a,b的真语言。L的基模型〈D,I〉满足：I(a)=¬Ta，I(b)=Ta。现考虑公式□(Ta∧¬Tb)→(□Ta∧□¬Tb)。

考虑ω+1长的E-修正序列模型N，其中H(w0)={I(a),I(b)}，N(wω)=‡W({w[A]|A⊆ω,sup(A)=ω,0/A}∪{w[A]|A⊆ω,sup(ω−A)＜ω})。与例4分析类似，可知N,wω□Ta、N,wω⊨□¬Tb、N,wω⊨□(Ta∧¬Tb)。从而有N,wω□(Ta∧¬Tb)→(□Ta∧□¬Tb)。故存在ω阶段不满足公理模式M的E-修正序列模型。

值得注意的是，在E-修正序列模型N 的ω阶段中，形如T┍φ∧ψ┑→(T┍φ┑∧T┍ψ┑)的语句不一定为真，即在ω阶段时T的外延并不对经典逻辑后承封闭。

对于公理N，由于⊤在任意可能世界上为真，且对任意非零序数β∈α，有W ∈N(wβ)，所以公理N在除初始阶段外的任意阶段相应的可能世界上均为真。

另外一个需要模拟的重要修正序列类为G-修正序列。在模拟G-修正序列时，由于G-修正序列在极限阶段不一定满足“对任意L中语句φ,ψ，如果这两个语句在一阶逻辑中等价，那么在极限阶段中对这两个语句的真假断定必须相同”这个要求。所以与B-修正序列类似，在定义G-修正序列模型时，需放宽“□～T”限制。

定义20(G-修正序列模型) 称α长的邻域序列模型N=〈W,N,D,V〉+ H为一个α长的G-修正序列模型，如果对任意0＜γ∈α，任意L中语句ϕ有：

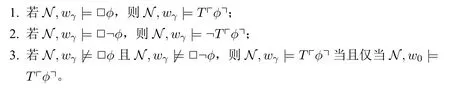
定理10 任给非零序数α，任意α长的G-修正序列模型均表示一个α长的G-修正序列；任给一个α长的G-修正序列，可以构造一个α长的G-修正序列模型表示它。

证明:证明过程与定理6的证明类似。 □

3 整体修正序列模型

通过上文的分析可知，对于任意的非零序数α，任给一个α长的经典修正序列，可以构造一个邻域语义模型表示它。类似地，对于任意α长的邻域基模型修正序列，也可以构造一个邻域语义模型表示它。

定义21(整体模型与整体假设) 给定一个真语言L的基模型〈D,I〉，任给非零序数α。称模型M=〈W,N−,N+,D,V〉为一个α长的整体模型，如果存在基于〈D,I〉的邻域基模型〈WB,N0,D,VB〉，使得W={wβ|w∈WB,β∈α}，且对任意序数γ∈α、任意w∈WB，有：

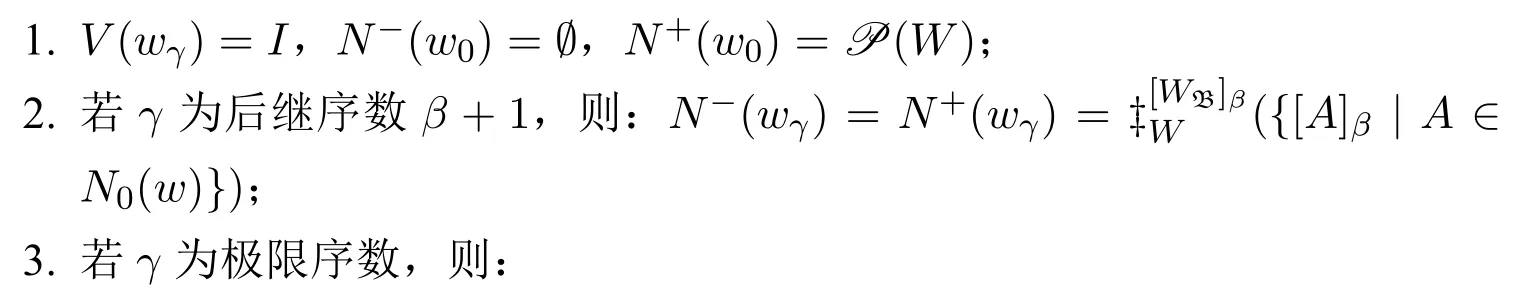
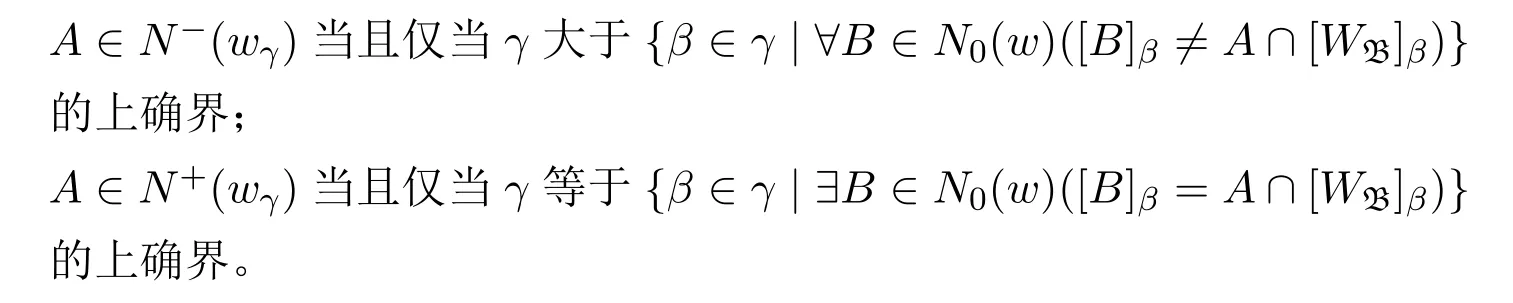
也称M为基于邻域基模型〈WB,N0,D,VB〉的α长的整体模型。

给定α长的整体模型M=〈W,N−,N+,D,V〉，若H为由W到P(Sent (L))的函数，则称H为M上的整体假设。若模型M′=〈W,N−,N+,D,V′〉，且对任意u∈W，〈D,V′(u)〉=〈D,V(u)〉+H(u)，则称把M′记作M+H。

定义22(整体序列模型) 若M为基于邻域基模型〈WB,N0,D,VB〉的α长的整体模型，H为M上的整体假设，则称N=M+H为基于邻域基模型〈WB,N0,D,VB〉的α长的整体序列模型，或简称α长的整体序列模型。

此处N为一个双模态词的固定论域邻域模型，故N上真值条件应为双模态词的邻域语义模型的真值条件。其中，邻域函数N−对应的模态词记作□−，邻域函数N+对应的模态词记作□+。我们仍把L增加了模态词□−和模态词□+所得的语言记作L□。

可知，当WB为单元集{w}且N0(w)={WB}时，定义21中的条件2和条件3将分别等价于如下两个条件：

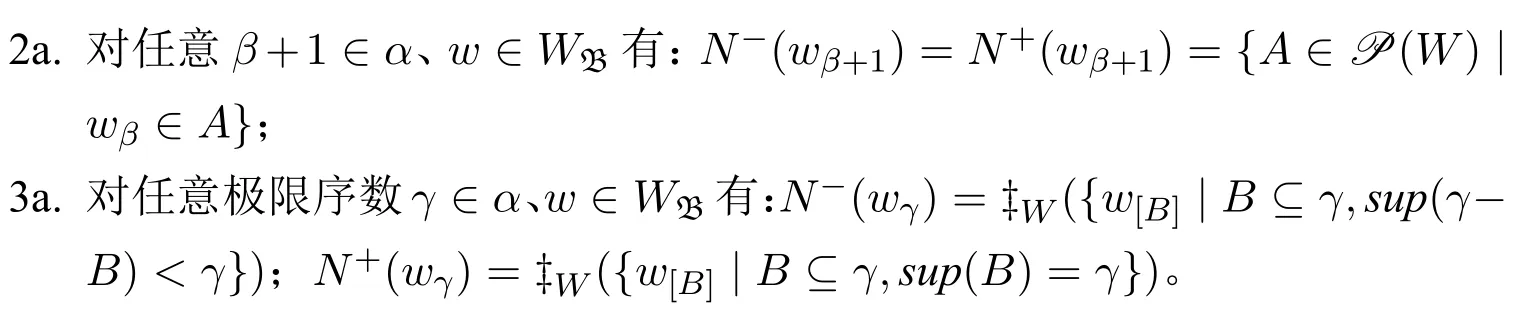
定义23(整体修正序列模型) 称一个基于〈WB,N0,D,VB〉的α长的整体序列模型N为一个α长的整体修正序列模型，如果对于任意序数γ∈α、w∈WB及任意L中语句ϕ有：

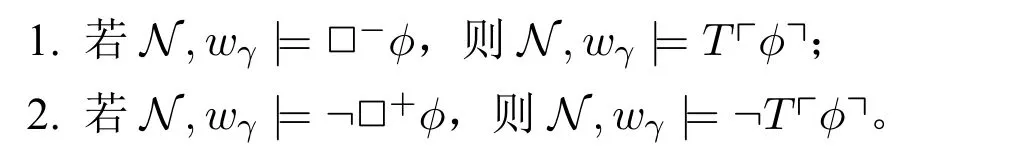
可知在一个整体修正序列模型中，当WB为单元集{w}且N0(w)={WB}时，对于任意序数γ∈α、w∈WB及任意L中语句ϕ有：N,wγ⊨□−¬ϕ当且仅当N,wγ⊨¬□+ϕ。这一点恰是上一章中的定义不需要给出两个邻域函数的原因。

定理11(整体修正序列模型定理) 任给非零序数α，任意一个α长的整体修正序列模型均表示一个α长的邻域基模型修正序列；任给一个α长的邻域基模型修正序列，可以构造一个整体修正序列模型表示它。

证明:定理11的证明过程类似于定理4，第一个命题中，相应需要证明的是〈Hγ〉γ∈α为一个α长的邻域基模型修正序列。后继阶段情形的证明和定理4证法相同，极限阶段情形的证明可通过定义21中的条件3得到。第二个命题中，相应需要证明的是：对任意γ∈α、w∈WB及L中语句ϕ，若N,wγ□−ϕ，则N,wγ⊨T┍ϕ┑；若N,wγ□+ϕ，则N,wγ¬T┍ϕ┑。γ=0时显然，后继阶段情形的证明和定理4证法类似，极限阶段情形的证明可通过定义21中的条件3得到。 □

目前为止定义的各种序列模型和各种修正序列模型都要求给出特定的长度非零序数α，未能表示全序数长的修正序列，故我们需要拓展我们之前的定义，使之能够表示全序数长的修正序列。不同于α长的序列模型，全序数长的“序列模型”需要一个真类作为“可能世界集”，相应的一个可能世界的邻域也可能是一个真类。所以在定义全序数长的“序列模型”并定义真值条件时，我们避免直接沿用固定论域邻域模型的定义。首先我们给出初始片段的定义。

定义24(初始片段) 给定任意两个非零序数α＜β，并且模型Nα=〈Wα,N−α,N+α,D,Vα〉+Hα为基于〈WB,N0,D,VB〉的α长的整体序列模型，模型Nβ=〈Wβ,N−β,N+β,D,Vβ〉+Hβ为基于〈WB,N0,D,VB〉的β长的整体序列模型。称Nα为Nβ的初始片段，记作NαNβ，如果：对于任意w∈WB, γ∈α：Hα(wγ)=Hβ(wγ)。

根据定义可知，若Nα为基于〈WB,N0,D,VB〉的α长的整体序列模型，Nβ为基于〈WB,N0,D,VB〉的β长的整体序列模型，且NαNβ，则对于任意w∈WB,γ∈α，有根据邻域语义的真值条件可知，对于任意w∈WB、γ∈α、L□中公式ϕ及任意指派σ，有Nα,wγσϕ当且仅当Nβ,wγσϕ。

定理12 任给非零序数α，对任意0＜γ∈α，Nγ为基于〈WB,N0,D,VB〉的γ长的整体修正序列模型，且对任意0＜β＜β′∈α，有NβNβ′。则存在基于〈WB,N0,D,VB〉的α长的整体修正序列模型Nα，使得：对任意0＜γ∈α，有NγNα。

证明:给定一个非零序数α，对任意0＜γ∈α，Nγ为基于〈WB,N0,D,VB〉的γ长的整体修正序列模型。根据定理11，Nγ表示了一个γ长的邻域基模型修正序列，记为Sγ。对任意0＜β＜β′∈α，由NβNβ′可得Sβ=Sβ′|β。故存在α长的邻域基模型修正序列Sα，使得对任意0＜γ∈α，Sγ=Sα|γ。再次根据定理11，存在一个α长的整体修正序列模型Nα表示修正序列Sα，根据初始片段的定义可知，对于任意0＜γ∈α，有NγNα。 □

定义25(全序数长的整体序列模型/整体修正序列模型) 给定一个全序数长的由基于〈WB,N0,D,VB〉的整体序列模型构成的序列〈Nγ〉0＜γ∈ON，且对任意非零序数α＜β，均有NαNβ。称为一个全序数长的整体序列模型，如果：

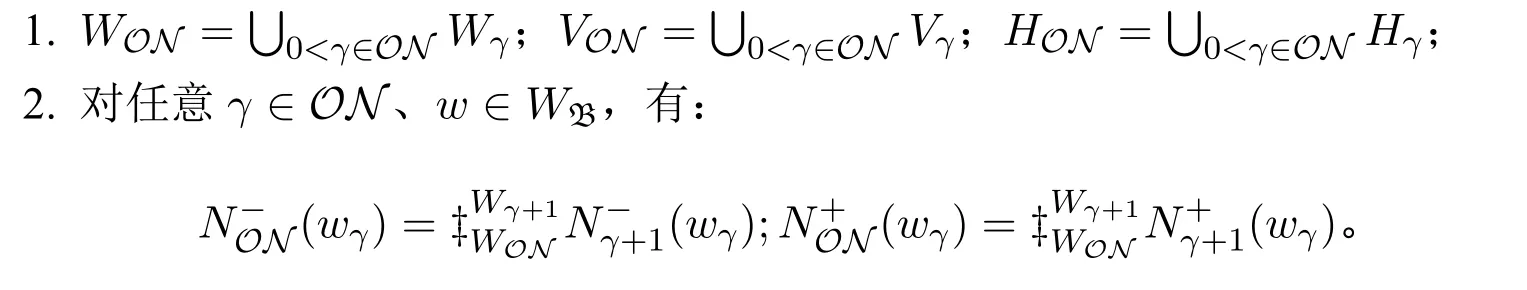
若每个Nγ(0＜γ∈ON)均为整体修正序列模型，则称NON为全序数长的整体修正序列模型。

该定义中的模型的“可能世界集”变成了一个真类，邻域函数也变成了类函数，所以不能直接沿用固定论域邻域模型的真值条件定义，但是根据“对任意非零序数α＜β，均有NαNβ”这个条件，我们可以给出全序数长整体序列模型的真值条件如下。

定义26(全序数长的整体序列模型的真值条件) 给定全序数长的整体序列模型NON，规定真值条件如下，对任意序数β∈ON，任意w∈WB，任意L□中公式ϕ，任意指派σ：

推论2 任意一个全序数长的整体修正序列模型，均表示一个全序数长的邻域基模型修正序列；任给一个（或一组）全序数长的邻域基模型修正序列，可以构造一个全序数长的整体修正序列模型表示它。

推论3 任给一个（或一组）全序数长的经典修正序列，可以构造一个全序数长的整体修正序列模型表示它。

至此，我们整合了第二部分内容中引入邻域语义研究修正真理论的两个不同路径，得到了整体修正序列模型类。该模型类中的模型可以用于表示任意一个或一组基于某个基模型M的经典修正序列或邻域基模型修正序列。

参考文献

[1] A.Chapuis,1996,“Alternative revision theories of truth”,Journal of Philosophical Logic,25(4):399–423.

[2] R.T.Cook,2002,“Counterintuitive consequences of the revision theory of truth”, Analysis,62(273):16–22.

[3] R.T.Cook,2003,“Still counterintuitive:A reply to Kremer”,Analysis,63(279):257–261.

[4] A.Gupta,1982,“Truth and paradox”,Journal of Philosophical Logic,11(1):1–60.

[5] A.Gupta and N.D.Belnap,1993,The Revision Theory of Truth,Mit Press.

[6] H.G.Herzberger,1982,“Notes on naive semantics”,Journal of Philosophical Logic, 11(1):61–102.

[7] M.Kremer,2002,“Intuitive consequences of the revision theory of truth”,Analysis, 62(4):330–336.

[8] E.Pacuit,2007,Neighborhood Semantics for Modal Logic:An Introduction.

[9] A.M.Yaqūb,1993,The liar speaks the truth:A defense of the revision theory of truth, Demand:Oxford University.

[10] 林其清，熊明，“克林强三值模式与修正过程”，世界哲学，2016年第4期，第152–159页。

[11] 王文方，“古朴塔及贝尔那普的真理修正理论述评”，欧美研究，2006年第36卷第1期，第75–120页。

[12] 熊明，塔斯基定理与真理论悖论，2014年，北京：科学出版社。

（责任编辑：任天鸿）

Neighborhood Semantics and the Revision Theory of Truth

Qiqing Lin
School of Politics&Administration,South China Normal University
linqiqing@foxmail.com
Xiaolong Liang
Institute of Logic and Cognition,Sun Yat-sen University
lianghillon@gmail.com

B81

A

2016-12-20

Gupta and Herzberg proposed the Revision Theory of Truth in 1982.They constructed revision sequences which can be used to analyze the concept of truth and related paradoxes.The Revision Theory of Truth classifies sentences according to their behavior in all revision sequences.The Revision Theory of Truth is unsatisfactory in the classification of some sentences.For example,The Revision Theory of Truth classifies the inverse proposition of Curry’s Paradox as categorical truth.This is considered as counterintuitive by some logicians.We will introduce the Neighborhood Semantics from two Paths to study the Revision Theory of Truth.First,we introduce neighborhood groundmodelsbasingongroundmodelsandconstructneighborhoodgroundmodelrevision sequences.The number of neighborhood ground model revision sequences is larger than that of classical revision sequences.The increased revision sequences can show that some sentence are pathological,such as the inverse proposition of Curry’s Paradox. Second,we introduce neighborhood semantics models such that,for any sentence without modality,the truth value of□ϕ at successor stage can reflect the truth value of ϕ at the previous stage,and the truth value of□ϕ at limit stage can reflect stability of ϕ before that stage.Hence,we can define different classes of models to represent different kinds of revision sequences,by putting different constraints on the relation between the truth values of T┍ϕ┑and□ϕ.We will integrate these two paths in the end of this paper. Andwewilldefineuniverserevisionsequencemodelstorepresentneighborhoodground model revision sequences.These two paths will be integrated in the end of this paper. We define universe revision sequence models to represent neighborhood ground model revision sequences.