滑动式与非滑动式GPS精密星历内插方法比较分析

徐炜,贾雪,严超,刘扬,杜文选,王涛

(安徽理工大学 测绘学院,安徽 淮南 232001)



滑动式与非滑动式GPS精密星历内插方法比较分析

徐炜,贾雪,严超,刘扬,杜文选,王涛

(安徽理工大学 测绘学院,安徽 淮南 232001)

本文在GPS卫星5 min精密星历的基础上,使用滑动式和非滑动式的Lagrange多项式插值法、Chebyshev多项式拟合法内插卫星的瞬时坐标,确定了内插精度与插值阶数的关系,并对各种方法的优缺点进行了比较分析。结果表明,滑动式内插算法能够抑制插值区间端点附近的振荡与跳跃异常,使用较低的插值阶数就可以达到最优的内插精度,在内插精度与稳定性方面都较非滑动式内插算法有所提高。

GPS;精密星历;滑动式算法;非滑动式算法;Lagrange插值;Chebyshev拟合

0 引 言

在利用GPS卫星进行导航定位时,需要准确地计算出卫星坐标,使用广播星历外推卫星瞬时坐标时的轨道误差较大,而根据IGS提供的精密星历内插卫星的瞬时坐标则可以达到较高的精度。

目前,使用精密星历求取卫星坐标的方法主要有非滑动式Lagrange多项式插值法、Chebyshev多项式拟合法两种,但在计算靠近插值区间两端点时刻的卫星坐标时,结果精度较低[1]。针对非滑动式内插算法存在的问题,本文研究了一种基于滑动式的Lagrange插值法、Chebyshev拟合法,并通过实例计算与非滑动式的内插算法进行了对比,验证了滑动式内插算法的可靠性。

1 插值与拟合算法原理

1.1 Lagrange多项式插值法

设y=f(xi)是区间[a,b]上的一个实函数,xi是[a,b]上的n个互异实数,且y=f(xi)在xi处的值为yi=f(xi),那么在区间[a,b]上的任意一点x的n阶Lagrange插值多项式的代数表达式为[2]

(1)

式中:xi为插值节点; 区间[a,b]为插值区间。

在进行n阶拉格朗日多项式内插任意时刻的卫星位置时,需要选取一个区间[ta,tb],使得t在区间内,并且在选择的区间内满足:插值节点数≥插值阶数+1[3]。该方法数学模型简单,但在插值节点数目变化时却需要重新构建多项式,卫星的瞬时坐标可以表示为

(2)

1.2 Chebyshev多项式拟合法

假定在时间间隔[t0,t0+Δt]的卫星轨道可用n阶Chebyshev多项式逼近,其中t0和Δt分别是开始历元和拟合时间区间的长度[4]。

先将t∈[t0,t0+Δt]变化成变量τ∈[-1,1],

(3)

则卫星坐标可以表示为

(4)

式中:n为多项式的阶数;Cxi,Cyi,Czi分别为x,y,z方向的Chebyshev多项式系数。Chebyshev多项式Ti,可以由下式推导出来:

T0(τ)=1,T1(τ)=τ,

T0(τ)=2τTn-1(τ)-Tn-2(τ); |τ|≤1,n≥2.

(5)

当插值节点数一定时,根据最小二乘理论,其误差方程为

V=BC+l，

(6)

式中:B为Chebyshev矩阵;l为残差向量。其法方程为

BTBC-BTl=0，

(7)

可以解算得到系数C为

C=(BTB)-1BTl.

(8)

将求解得到的系数C代入上式,就可以求出拟合区间内任意时刻的卫星三维坐标[5-6]。

1.3 滑动式内插算法

非滑动式Lagrange插值、Chebyshev拟合内插算法都是固定一个插值区间,利用该区间内的已知插值节点坐标来内插出区间内部的待插值点坐标。该算法的最大缺陷在于,在插值区间端点附近处的内插精度会变差,坐标值会出现较大的波动,而滑动式内插算法则可以克服这个缺点。

图1 滑动式内插算法原理图

滑动式内插算法就是通过不断的变换插值区间,使得待插值点始终位于插值区间的中心位置,以此来提高插值精度[7-8]。如每次取12个插值节点,生成11阶插值多项式,那么最佳的插值段就位于第6个插值节点与第7个插值节点间的中间区域,只使用第6个插值节点与第7个插值节点间的插值点作为计算结果,将其他节点处计算的结果进行舍去。并一直保持这个插值区间的大小不变,每次将插值区间向后移动等间隔的距离,使得待插值点始终位于插值区间的中间位置,其原理如图1所示[9-10]。

2 算例分析

本文采用由JAXA提供的2015年12月28日0时0分0秒至2015年12月29日23时45分0秒采样间隔为5 min的SP3精密星历数据,以PRN20号卫星作为实验对象进行插值实验。插值与拟合的区间为12月29日0时0分0秒至12月29日3时0分0秒,其余数据为满足滑动式内插算法所需要的数据。

由于精密星历的采样间隔为5 min,为了比较内插结果的精度,选取12月29日0时0分至12月29日每隔10 min间隔的卫星位置作为插值节点(共19个插值节点),将每隔5 min间隔的卫星位置作为已知数据进行检核。选择滑动式与非滑动式的Lagrange插值法、Chebyshev拟合法计算出3 h内每隔5 min的卫星坐标,并将计算出的卫星坐标与精密星历的卫星坐标进行对比,求出残差值及RMS值,具体流程如图2所示。

图2 卫星坐标插值计算流程图

2.1 非滑动式内插算法精度分析

2.1.1 非滑动式Lagrange插值精度分析

在用Lagrange多项式内插卫星位置时,由于插值阶数受到插值节点数的限制,一般n个插值节点最大能够达到n-1阶。从12月29日0时0分0秒起开始依次选取6个插值节点至19个插值节点,以实现5阶～18阶的非滑动式Lagrange多项式插值,并分析不同的插值阶数对内插精度的影响,非滑动式Lagrange多项式不同阶数时的内插值精度如表1所示。

表1 不同阶次Lagrange多项式内插结果

为了形象地表现出内插精度的变化过程,图3示出了三维方向上的非滑动式Lagrange多项式内插精度的变化曲线。

不比不知道，一比吓一跳。在茄子移栽后34天，洋丰百倍邦套餐肥展现了强劲效果。观摩会当天，众人冒着高温，在新洋丰工作人员带领下来到茄子示范田。刚进入茄子地，众人就被左右两块茄子地长势差距震惊了，示范田茄子植株明显比对照田要高出一大截。在众人惊奇之余，卢琼珍高兴地为观摩人员介绍示范田和对照田的施肥方案。他一共租80亩地，其中一半转租出去。因卢琼珍是新洋丰肥料零售商，剩余40亩地在新洋丰技术员指导下，施用了百倍邦套餐肥。

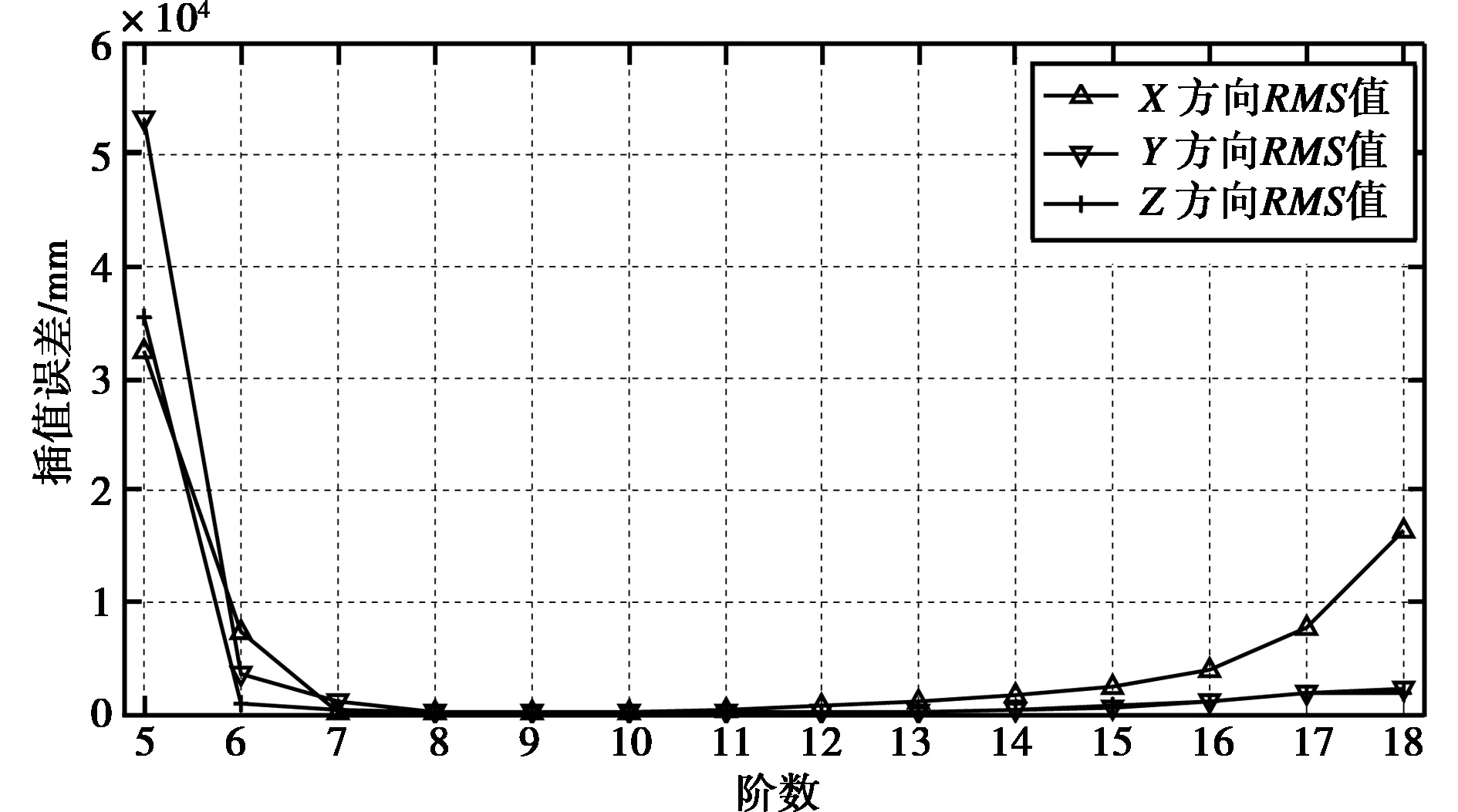
图3 非滑动式Lagrange插值法RMS值随阶数变化曲线

从表1和图3可知,随着插值阶数的增加,内插精度先增加后减小,在阶数为9时的内插精度最高,三维坐标分量达到最佳插值精度的阶数也不完全相同;非滑动式Lagrange多项式内插时在区间两端出现了较大误差,通过将端点处数据剔除后的RMS值与未剔除的RMS值对比可以发现,插值区间段中间部分的插值精度较为理想,故在实际应用中应将区间两端的插值点踢除,尽量使用中间部分的数据。

2.1.2 非滑动式Chebyshev拟合的精度分析

在使用非滑动式Chebyshev拟合法内插待定点的卫星坐标时,应满足拟合节点数≥拟合阶数+1,内插精度与插值节点数以及插值阶数具有密切的关系。为了说明内插精度与插值阶数的关系,依次选取0:10、0:20、…、3:00等19个已知点作为插值节点,选择插值阶数为8、9、…、18,内插出5 min间隔的卫星坐标,并与5 min间隔的精密星历提供的坐标对比,得出残差值与RMS值,计算结果如表2、图4所示。

表2 不同阶次Chebyshev内插结果

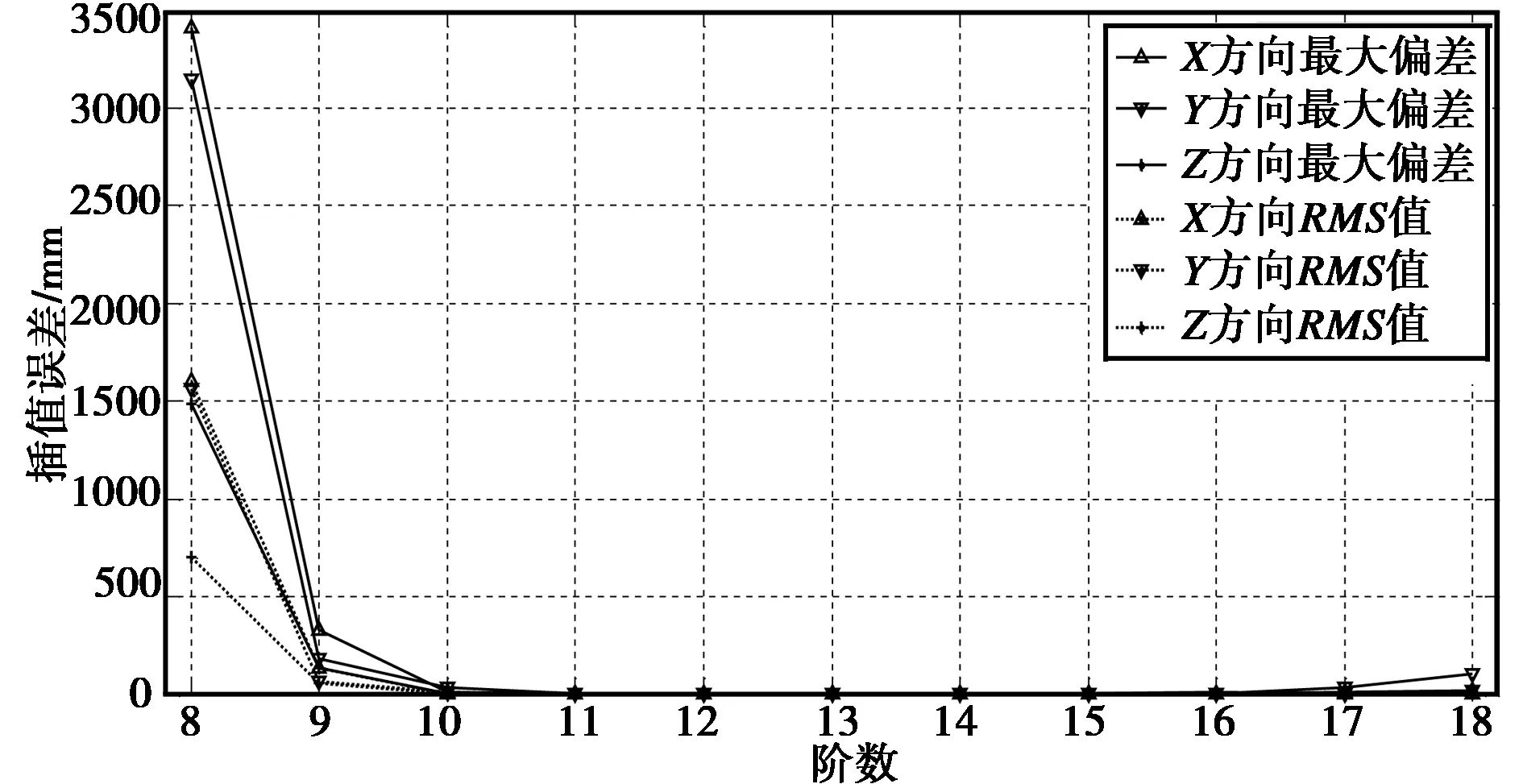
图4 非滑动式Chebyshev多项式RMS值随阶数变化曲线

从表3、图4可知,随着插值阶数不断的变化,内插精度也随之变化。8～13阶时的内插精度逐渐提高,13～18阶时的内插精度又逐渐变差,与非滑动式Lagrange插值法内插精度随阶数的变化趋势基本一致,但非滑动式Chebyshev拟合法的内插精度要优于非滑动式Lagrange插值法的内插精度;在11～15阶时的三维坐标分量内插精度都在1 mm以内,优于精密星历的坐标误差,完全能够满足精密单点定位的要求;同时发现三维方向达到最佳内插精度时的插值阶数并不相同,在实际应用中可以对三维坐标分量分别选取不同的插值阶数,已到达期望的内插精度。

2.2 滑动式内插算法精度分析

2.2.1 滑动式Lagrange插值精度分析

选取0:10、0:20、…、3:00这些点作为插值节点,使用滑动式Lagrange插值法内插出3小时内每个5 min间隔的插值点卫星坐标。滑动式Lagrange插值需要保证在每隔插值区间的前后都要有相同的插值节点,如在使用11阶Lagrange多项式内插0:00-0:10时间段内的卫星坐标时,向左选取28日22:00-23:00的6个插值节点,向右选取29日0:10-1:00的6个插值节点。对于插值节点处的卫星坐标不进行插值,使用精密星历提供的数据,计算出插值点处卫星坐标与精密星历所提供卫星坐标的残差值与RMS值,计算结果如表3、图5所示。

表3 不同阶次滑动式拉格朗日内插结果

图5 滑动式Lagrange多项式RMS值随阶数变化曲线

从表3、图5可以看出,随着插值阶数的增加,内插精度不断提高。在5阶以下时,滑动式Lagrange插值法内插结果有较大误差,最大的RMS值达到1 m左右。当插值阶数达到7时,RMS值已经能够达到毫米级;当插值阶数在9～15时,三维坐标分量的RMS值基本稳定在毫米量级。滑动式Lagrange的内插结果优于非滑动式Lagrange的内插结果,高次插值时也没有出现“龙格现象”。此外,由于增加插值阶数会相应的增加计算量,因此建议在实际使用中在满足内插精度的情况下尽量选择较低的插值阶数。

2.2.2 滑动式Chebyshev拟合的精度分析

选取0:00-3:00内10 min倍数的时间点作为插值节点,使用滑动式Chebyshev插值法内插出3小时内每个5 min间隔的插值点卫星坐标,并计算出插值点处的残差值与RMS值,计算结果如表4、图6所示。

表4 不同阶次滑动式Chebyshev内插结果

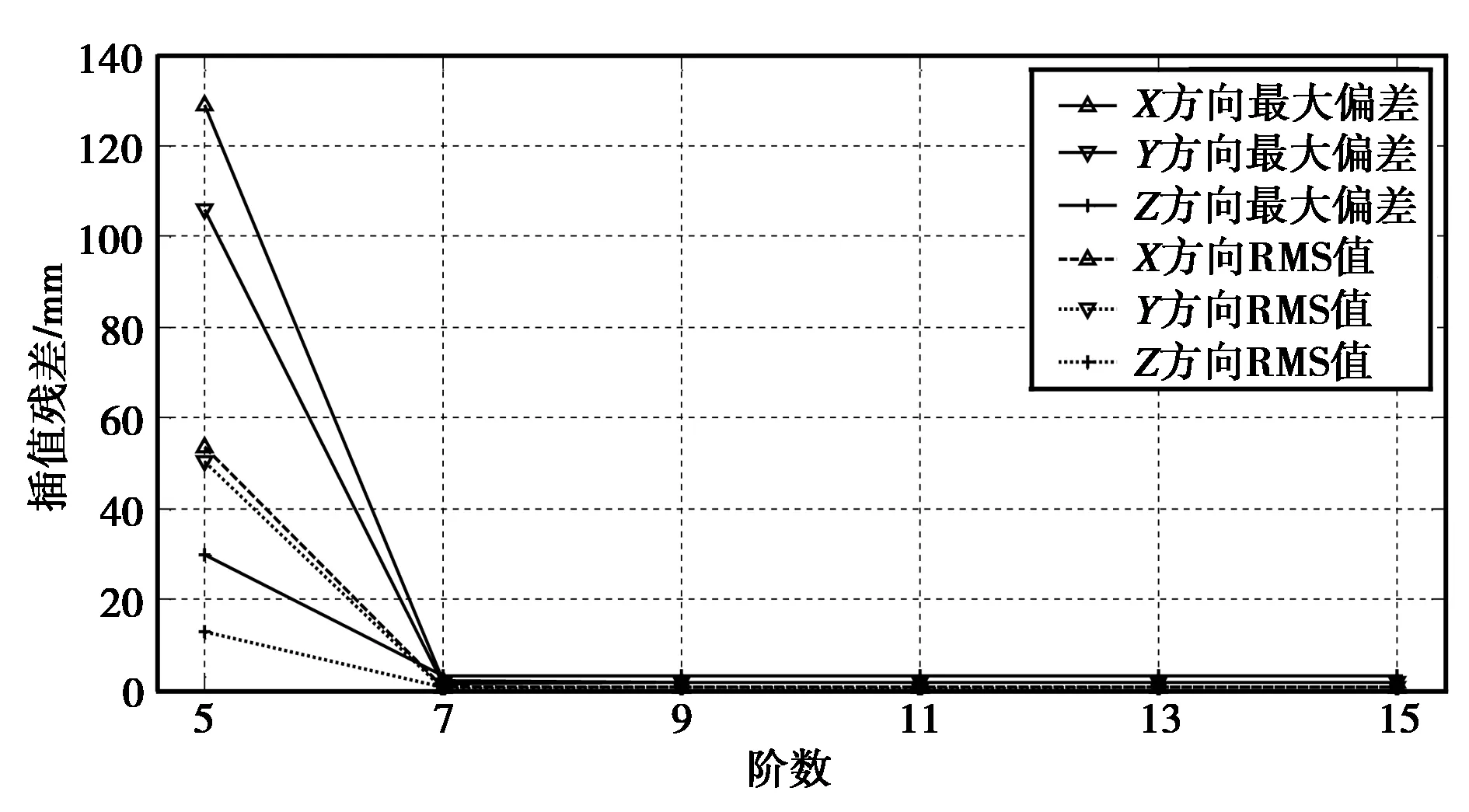
图6 滑动式Chebyshev多项式RMS值随阶数变化曲线

从表4、图6可以看出,5～9阶之间的RMS值随着插值阶数的增加而不断增加,9～15阶时的RMS值趋于稳定,约在1 mm以内。滑动式Chebyshev拟合法比滑动式Lagrange插值法的内插精度要高,两种方法的RMS值随插值阶数的变化趋势完全一致。滑动式Chebyshev法与非滑动式Chebyshev法内插精度相当,而达到相同内插精度时所用的插值阶数更小,不会出现随插值阶数的增加内插精度变差的情况。

2.3 滑动式与非滑动式方法内插精度对比分析

为了对滑动式与非滑动式内插算法的内插性能进行比较,选取滑动式与非滑动式Lagrange插值法、Chebyshev拟合法RMS值最小时的阶数作为插值阶数,计算出待插值点的卫星坐标及与精密星历坐标的残差值。非滑动式内插算法的残差分布如图7所示,滑动式内插算法的残差分布如图8所示。

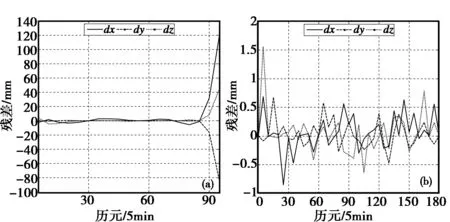
图7 非滑动式内插方法残差图(a)9阶非滑动式拉格朗日插值法残差分布图(b)13阶非滑动式Chebyshev拟合法残差分布图

图8 滑动式内插方法残差图(a)9阶滑动式拉格朗日插值法残差分布图(b)13阶滑动式Chebyshev拟合法残差分布图

从图7、图8可知,非滑动式拉格朗日插值算法在末端产生了较大的误差,卫星坐标残差产生了较大跳跃,而滑动式拉格朗日插值算法的残差分布则相对稳定;滑动式拉格朗日插值算法在靠近插值区间的端点虽然也有些波动但相对于残差值的总体变化而言,波动的幅度并不大,已经能够满足导航定位的要求;滑动式Chebyshev多项式拟合算法与非滑动式Chebyshev多项式拟合算法内插的残差值基本相同,滑动式的算法残差分布更稳定一些;滑动式Chebyshev多项式拟合算法较滑动式拉格朗日插值算法的计算结果精度稍高,波动也更小;滑动式算法精比非滑动式算法的内插精度要高,因此,建议在实际的应该中优先使用滑动式内插算法,避免使用高阶非滑动式拉格朗日算法。

3 结束语

1) 滑动式内插算法与非滑动式内插算法相比,使用较小的插值阶数就可以达到最优的插值精度,计算效率更高,能有效的抑制插值区间端点处的振荡和跳跃现象。

2) 使用滑动式与非滑动式内插算法计算待插值点坐标时,在一定的阶数内,内插精度随着插值阶数的增加而逐渐提高,但当插值阶数达到一定数值时,随着插值阶数的增加,滑动式内插精度逐渐趋于稳定,非滑动式内插精度出现了下降趋势。

3) 卫星的三维坐标分量在取同一插值阶数时的内插精度不同,达到最佳插值精度时所取的插值阶数也并不相同,在内插卫星坐标时可以对三个坐标分量选取不同的插值阶数,以达到最佳的插值精度。

[1] 孙腾科.基于拉格朗日与切比雪夫的精密星历插值研究[J]. 测绘与空间地理信息,2014,37(2):33-37.

[2] 王威,陈明剑,闫建巧,等.北斗三类卫星精密星历内插方法比较分析[J]. 全球定位系统,2016,41(2):60-65.

[3] 万亚豪,张书毕,候东阳.基于GPS广播星历的卫星位置拟合精度分析[J]. 测绘工程,2011,20(3):38-40.

[4] 任锴,杨力,郭玉良,等.GPS卫星星历计算研究[J]. 海洋测绘,2008(1):31-34.

[5] 余鹏,孙学金,赵世军.GPS定位中卫星坐标计算的切比雪夫多项式拟合发[J]. 气象科技,2004,32(3):198-201.

[6] 严丽,李萌.切比雪夫多项式拟合卫星轨道与钟差的精度分析[J]. 测绘科学,2013,38(3):59-62.

[7] 王兴,高井祥,王坚,等.利用滑动式切比雪夫多项式拟合卫星精密坐标与钟差[J]. 测绘通报,2015(5):6-8,16.

[8] 彭小强,高井祥.基于滑动式切比雪夫方法的广播星历插值分析[J]. 煤炭科技,2015,34(6):104-106.

[9] 何玉晶,杨力.基于拉格郎日插值方法的GPS IGS精密星历插值分析[J]. 测绘工程,2011,20(5):60-62,66.

[10] 雷雨,赵丹宁,高玉平.基于滑动式Lagrange插值方法的GPS精密星历内插分析[J]. 测绘工程,2013,22(2):34-36.

The Method of Comparative Analysis Sliding and Non Sliding GPS Precise Ephemeris Interpolation

XU Wei,JIA Xue,YAN Chao,LIU Yang,DU Wenxuan,WANG Tao

(SchoolofGeodesyandGeomatics,AnhuiUniversityofScienceandTechnology,Huainan232001,China)

Based on the 5-minute precision ephemeris of GPS satellites, this paper uses Lagrange polynomial interpolation with the type of sliding and non-sliding and Chebyshev polynomial fitting method to calculate the instantaneous coordinates of the satellites. The relationship between the precision of interpolation and interpolation order is determined, then the advantages and disadvantages of various methods are compared and analyzed. The results show that the interpolation algorithm with the type of sliding can suppress the oscillation and jumping anomaly near the endpoints in the Interpolation interval and making use of lower interpolation order can achieve optimal interpolation accuracy, in addition, both interpolation accuracy and stability are improved compared to the algorithm of non-sliding interpolation.

GPS; precise ephemeris; sliding algorithm; non sliding algorithm; Lagrange interpolation; Chebyshev fitting

10.13442/j.gnss.1008-9268.2017.02.004

2016-12-26

国家自然科学基金(批准号:41474026); 淮南矿业(集团)有限责任公司项目(编号:HNKY-JTJS(2013)-28); 安徽省国土资源厅科技项目(编号:2011-K-22;2011-K-18);安徽理工大学研究生创新基金(编号：2017CX2056)

P228.4

A

1008-9268(2017)02-0015-06

徐炜 (1992-),男,安徽芜湖人,硕士生,主要研究方向为GNSS导航与数据处理。

贾雪 (1990-),女,河南周口人,硕士生,主要研究方向为大地测量学与测量工程。

严超 (1993-),男,安徽滁州人,硕士生,主要研究方向为 GNSS 导航与数据处理。

刘扬 (1991-),男,山东莱芜人,硕士生,主要研究研究方向为 GNSS 数据处理。

杜文选 (1992-),男,安徽宿州人,硕士生,主要研究方向为 GNSS 导航与定位。

王涛 (1992-),男,安徽六安人,硕士生,主要研究方向为 GNSS 导航与数据处理。

联系人: 徐炜E-mail:1157896096@qq.com