单星频差无源定位技术原理及仿真
2017-06-05蒋东旭谢登召
蒋东旭,谢登召
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225001)
单星频差无源定位技术原理及仿真
蒋东旭,谢登召
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225001)
鉴于卫星技术的快速发展和广泛应用,利用卫星无源定位系统以适应当今高科技战场对电子战武器的隐蔽攻击的需求已经成为一个重要的发展方向,而单星无源定位系统具有成本低、灵活性好等优点,成为研究的热点。研究单星频差无源定位原理和定位方法,针对定位模糊问题提出了解决方案,分析了影响定位精度的因素并推导了定位的理论误差和圆概率误差。
单星;无源定位;频差;误差分析;仿真
0 引 言
现代战争是海、陆、空、电磁波的四维一体化战争,快速、准确地获取目标的位置是战争获胜的必要条件。无源定位技术以其不辐射电磁波信号,因而具有良好的隐蔽性,这大大提高了作战平台在复杂电磁环境下的生存能力。
星载无源定位系统以卫星平台为载体,对地面辐射源进行无源定位,具有全天候、全天时、作用距离远、覆盖范围广等特点。在星载无源定位系统中,常采用干涉仪测向或时差对地面辐射源进行定位。干涉仪测向定位算法简单,在单星条件下即可完成测向定位,但这种比相法测向对各通道间的相位一致性有着严苛的要求;而时差定位则需要多颗卫星在空间满足一定的几何关系才能完成定位,使用受限而且成本高,并且需要高精度的时统,这限制了其工程应用。
单星测频定位利用卫星平台和地面辐射源之间相对运动所产生的多普勒效应对辐射源进行定位。在低轨情况下,卫星飞行速度快,产生的多普勒频率大,有利于提高定位精度。此外,单星降低了系统成本,提高了可靠性。本文从单星频差无源定位的原理入手分析了定位模糊问题,并针对相关解决方案,采用蒙特卡洛法仿真研究了定位精度的影响因素。
对辐射源的定位信息,可以直接用于对敌武器平台的精确打击,引导反辐射武器攻击以及建立战场电子战斗序列(EOB)等。科技的进步和实战需要推动了无源定位技术的发展,无论是利用外辐射信号对目标的定位,还是利用目标自身辐射信号对目标的定位技术,都有长足的发展和创新。
1 单星频差无源定位原理
对于一个静止在地面或空中的辐射源,卫星在N个不同的时间测量信号到达卫星的频率,与这些频率对应的等频面是N个锥顶在卫星处,锥面过辐射源的圆锥面,并且由于卫星的运动,这N个圆锥角互不相等。因此从理论上讲,若辐射源频率已知,那么当N≥3时,可以确定空中静止辐射源的位置;当N≥2时,可以确定地面静止辐射源的位置。若辐射源频率未知,可以用测量的多普勒频率对它估计,然后计算辐射源位置或在估计f的同时进行定位计算。一般地,当N≥4时,可以在辐射源频率未知的情况下确定空中静止辐射源的位置;当N≥3时,可以在辐射源频率未知的情况下确定地面上静止辐射源的位置。下面的讨论都假定辐射源频率未知,定位计算时用测量的多普勒频率对它估计[2]。
当N=4时,由4个多普勒频率可以得到3个独立的频差(FDOA),并且对应的3个互不相同的等频差面在辐射源处相交,因此也可以用3个等频差面对三维空间中的1个静止辐射源定位;当N=3时,可以用2个等频差面对地面上的1个静止辐射源定位[2]。
以上就是单星频差无源定位的等频率锥面定位和等频差面定位的几何原理。这里讲的定位实际上包含了2个位置,即辐射源的位置和它与卫星轨道面对称点的位置,应采用其它信息剔除其中的镜像位置。本章采用最小二乘法的单星频差无源定位计算方法。
如图1所示,地面上静止的辐射源S在地表,设OS=r,S在坐标系中的坐标为(x,y,z),对应的经纬度为(λ,φ),x=a·cosφcosλ,y=a·cosφsinλ,z=b·sinφ,a=6 378 km,b=6 357 km,卫星进行第i次测量时的位置Pi的坐标是(xi,yi,zi),速度是vi=(xi,yi,zi)T,并记OS=r,OPi=ri,ui=(r-ri)/‖r-ri‖,其中‖x‖表示矢量x的模。那么信号的传播时延为[2]:
τi(t)≈(‖r-ri‖-(vi·ui)·t)/c
c=3×108m/s,i=1,…,N
(1)
式(1)可以表示成τi(t)≈‖r-ri‖/c-‖vi‖/c·cosαi·t,αi是vi与ui之间的夹角。
如果辐射源发射的信号为S(t),那么卫星在Pi处接收到的信号为[2]:
Si(t)=S[t-τi(t)]
(2)
若S(t)=A(t)·cos[2πf·t+φ(t)],其中A(t)和φ(t)都是慢变函数,即S(t)是窄带信号,那么在第i次的短暂测频时间内,有:
Si(t)=S[t-τi(t)]≈Ai·cos{2πf· [1+(vi·ui)/c]·t+φi-2πf·‖r-ri‖/c}
(3)
式中:Ai和φi分别为在第i次测频时A(t)和φ(t)的初始值。
通过对Si(t)测频,可得到:
fi=f·[1+(vi·ui)/c]+εi
(4)
式中:fi为第i次测量的频率;f为辐射源的天线辐射的信号频率;εi为第i次测频的误差。
式(4)还可以表示为:
fi≜f·gi(x,y,z)+εi,i=1,…,N
(5)
2 单星频差无源定位计算方法
将式(5)写成如下矩阵形式[2]:
F=G·f+E
(6)
式中:F=[f1,…,fN];G=[g1(x,y,z),…,gN(x,y,z)]T;E=[ε1,…,εN]T,上标T表示矩阵转置。
当N≥4时,在包含辐射源的位置范围内划分网络,给定网格点集Ω,对每个网格点(xk,yk,zk)∈Ω,计算f的最小二乘解:
(7)
式中:Gk=[g1(xk,yk,zk),…gN(xk,yk,zk)]T;x-1表示矩阵x的逆。
辐射源的位置由下式估计:
(8)


3 模糊点的去除
按照上节所叙述的方法,会得到2个定位点:一个为目标的真实点;另一个为目标的镜像点,即模糊点。定位模糊点是由单星频差定位的几何原理造成的,通过算法本身无法去除模糊。这2个定位点是相对卫星星下轨迹对称的,根据这个特点,有如下2种去模糊的方案[3]:
方案一:增加测向信息,判断卫星的方向,从而去除模糊点。如图2所示,可以使卫星的接收天线主瓣偏向左或向右一侧,另外一侧的定位模糊点则在天线的副瓣方向,从模糊点处辐射的信号无法到达卫星接收机,从而在定位求解过程中就可以去除模糊点。
方案二:如果卫星上采用全向天线,则可以利用多个轨道面观测的结果来解模糊。如图3所示,卫星第1次经过地面辐射源上空时在地面的轨迹为卫星轨迹1,在t11和t12时刻分别形成的等频锥线的交点为A和B,此时无法判断哪一点是目标的真实点:由于定位体制采用的卫星是低轨道(LEO)卫星,当卫星第2次经过地面辐射源上空时在地面的轨迹为卫星轨迹2,在t21和t22时刻分别形成的等频锥线的交点分别为A和C,联立2次的定位结果,他们共同的交点A即为目标的真实位置,从而排除了模糊点。当然,如果同时有2颗LEO卫星进行定位,依照同样的原理,联立2个卫星的定位结果同样可以去除模糊点。
具体采用哪种方案根据卫星及使用者的用途等具体情况而定。
4 单星频差定位误差分析
单星测频无源定位系统的误差来源是多方面的,根据来源分为4类,如表1所示[3]。
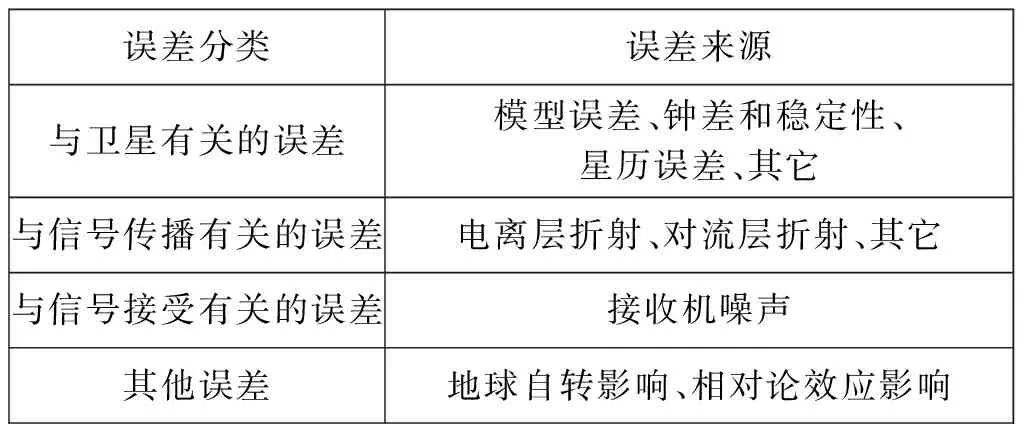
表1 单星测频无源定位误差来源
从误差的性质来分类,上述误差又可分为系统误差和随机误差。对于系统误差可以建立相应的系统误差模型,对观测量加以修正,也可以采用其它方法削弱或消除有关系统误差的影响。本文主要基于单星测频无源定位原理中的随机误差进行分析,对于系统误差的修正和消除不再深入研究。
4.1 误差的C-R界
假定ε1,…,εN∈N(μ,σ2),那么f1,…,fN的联合概率密度函数为:
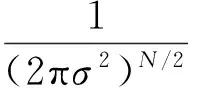
(9)
于是有:
(10)
不考虑卫星位置和速度误差,记[f,x,y,z]=[μ1,μ2,μ3,μ4],那么:
(11)
Fisher信息矩阵F的第mn个元素为:
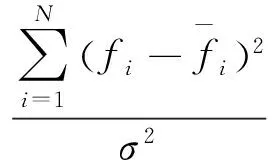
(12)
对于给定的μm,其C-R界是(F-1)mn[3]。
4.2 定位均方根误差
星载雷达测频接收机的测频误差与测频信道的信噪比、系统通道一致性等因素有关。对于不同的测频接收机,详细影响关系可参见参考文献[4]。因此,下面的误差分析和仿真只分析测频均方根误差与定位误差的影响关系。
由于定位误差涉及f的估计误差,为方便计,只对先用N个测频数据估计f,再由2个等频差面确定地面上静止辐射源位置的情况进行误差分析。以下取N=3,N≥4时可以用相同的方法讨论。记qi=fi+1-fi,i=1,2,即:

(13)
由q1,q2确定的2个定位曲面和地球球面在S处相交。测频误差、卫星位置误差或卫星速度误差将引起定位曲面变动,当这种变动较小时可以用S处的定曲面沿它的法向(梯度方向)移动来近似。
将式(13)表示为:
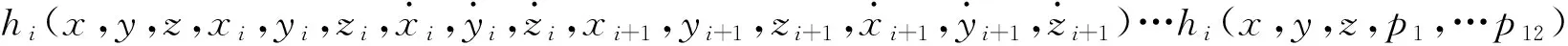
对qi求全微分,得:
Δqi=
(14)
式中:Δu=(Δx,Δy,Δz);hi=[-];=[(vi+1·ui+1)-(vi·ui)]。
若设Δu在hi上的分量为ni,那么有:

(15)

用ni和u可以确定定位曲面移动后与地球球面交线位置偏移的矢量mi为:

(16)
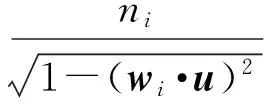
式(16)推导过程见参考文献[2]的附录。
因此定位的距离误差为:

(17)
式中:θ=〈m1,m2〉。
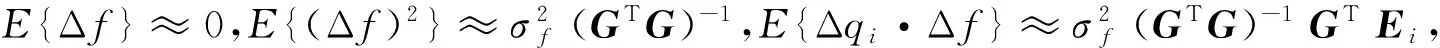
(18)

(19)
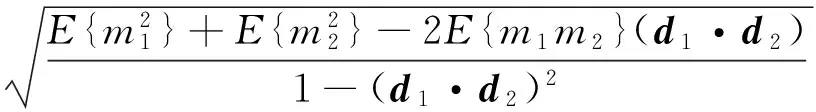
(20)
显然,根据式(18)~(20)可知,当不考虑卫星位置和卫星速度误差时,定位均方根误差与测频均方根误差成正比[2]。
4.3 等概率误差椭圆
将式(4)表示成[5]:
fi≜gi(f,λ,φ)+εi,i=1,…,N
(21)
将式(21)写成矩阵形式:
f=g(f,λ,φ)+ε
(22)
式中:f=(f1,…,fN)T;g(f,λ,φ)=[g1(f,λ,φ),…,gN(f,λ,φ)]T;ε=[ε1,…,εN]T。
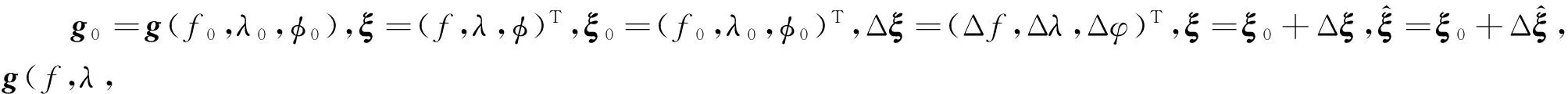
f≈g0+J·Δξ+ε
(23)
若M是ε的协方差矩阵,那么Δξ的最小二乘估计为:
(24)
ξ的估计为:
(25)
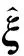
b1=(JTM-1J)-1JTM-1(g-g0-J·Δξ+E(ε))
(26)
当ξ0=ξ(即Δξ=0)且E(ε)=0时,b1=0,其中E为数学期望算子。
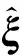
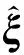
(27)
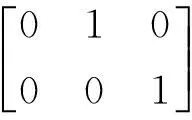
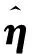
(28)
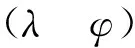
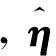
(29)
式中:R={y:(y-η)TΣ1-1(y-η)≤k}。
比较常用的是圆概率误差(CEP)[6],它的表达式为:

(30)
其中,令γ=λ2/λ1,当γ≥0.3时,估计偏差小于1%;当0.1<γ<0.3时,估计偏小且偏差低于10%;当γ为其它值时,估计偏小且偏差低于20%。一种更好的近似,对所有的γ而言,其估计偏差近似为10%:
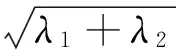
(31)
其中,当CEP比γ≈0.4大时,上式的近似偏小,当CEP比γ≈0.4小时,上式的近似偏大。
5 仿真分析
5.1 仿真思路
定位原理仿真时采用蒙特卡洛仿真方法,首先依据1节的单星频差定位原理产生卫星在不同位置处测得的地面静止辐射源辐射的电磁波的多普勒频率(包含有测频误差),这里的多普勒频率样本采用蒙特卡洛仿真原理产生一定组测量值,其中每组的值的数量相等且各组对应处的值是卫星在同一位置得到的;其次,依据2节的单星频差定位计算方法进行定位,定位时分2步,先进行粗定位,即在较大范围内且网格间隔划分比较大的情况下,得到卫星的初步位置定位,依据已知的其他信息排除定位的虚假点,再次进行精定位,即在粗定位中得到的初步定位位置附近将网格细分,得到精确位置定位;最后,将每个样本得到的精定位点做平均估计,得到最终定位点。
定位误差仿真时依据4.2节给出的定位误差公式,首先保持辐射源位置和测频误差不变,利用“滑动窗”的方式,即将多个位置得到的测量值进行划分,每次取连续3个位置的值得到1个定位误差均方根值,然后向后滑动,以上次第2个值为下一次的第1个值重复上述过程,这样便得到一系列的定位误差均方根值,将它们取平均即得到最终的1个定位误差均方根值;其次改变测频误差的均方根值即得到某一确定测频点数和确定辐射源位置的误差曲线;再次改变测频点数得到不同测频点数定位误差曲线;最后保持测频误差和测频点数一定,改变辐射源位置得到定位误差随辐射源和卫星轨迹相对位置的分布曲线。
5.2 定位原理仿真
为了便于仿真,假定地球为无旋圆球,平均半径为R=6 371 km,不考虑卫星位置和速度误差。卫星在地球上空高度为500 km的圆形轨道上飞行,辐射源天线发射的信号频率为f=1 GHz,卫星对辐射源进行了21次的频率测量,相邻2次测量的时间间隔为5 s,频率的测量误差独立,是分布于N(0,(200 Hz)2)的高斯随机变量。辐射源位置坐标是(133.5°,29.3°),进行1 000次蒙特卡洛仿真,卫星飞行轨迹如图4,单星频差定位粗定位、精定位结果如图5和图6。
由仿真结果知,单星频差定位会产生2个定位点,通过其它信息排除1个点后进行精定位。精定位的结果不易从图中观察得到,通过对仿真参数的Z坐标数据进行分析后得到仿真定位点坐标为(133.51°,29.29°),定位误差为1.475 km,这里受仿真的硬件平台(个人PC)处理数据速度能力的限制,网格划分不够精细,仿真次数不够多,影响了定位的精度,但是已经验证了单星频差定位原理与定位计算方法的正确性。
5.3 定位误差仿真
仿真时仿真条件仍与上一小节定位原理与仿真条件类似,改变测频误差的均方根值即测频误差服从的高斯分布的标准差值以及测频点数N,得到图7。
由图7知,测频误差均方根值与定位误差近似成正比,验证了式(20)。并且随着测频点数N的增加,定位误差均方根值减小。假定测频误差的均方根值为200 Hz,测频点数为21,改变地面上静止辐射源的位置坐标,得到图8。由图7,图8可知,定位误差以卫星轨迹为对称轴,辐射源与卫星轨迹的相对位置越远定位误差越大,越靠近星下点位置定位误差越大。
6 结束语
本文主要介绍了单星频差无源定位的原理和方法,并给出了定位原理实现的算法-网格搜索法和由于定位原理自身问题造成的定位模糊点的2种解决办法。对定位误差进行了定量分析,仿真并验证了单星频差无源定位原理和定位计算方法的正确性,最后通过定位误差曲线直观地表明了定位误差随影响定位精度因素的变化关系。
[1] 杨弘.单站/多站无源定位跟踪研究[D].重庆:重庆邮电大学,2011.
[2] 陆安南,孔宪正.单星测频无源定位法[J].通信学报,2004,25(9):160-168.
[3] 李献斌.单星测频无源定位技术研究[D].长沙:国防科技大学,2009.
[4] 赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,2005.
[5] 陆安南,杨小牛,等.单星测频测相位差无源定位[J].系统工程与电子技术,2010,32(2):244-247.
[6] TORRIERI D J.Statistical theory of passive location systems[J].IEEE Transactions on Aerospace Electronic System,1984,20(2):183-198.
Principle and Simulation of Single Satellite Frequency Difference Passive Location Technology
JIANG Dong-xv,XIE Deng-zhao
(The 723 Institute of CSIC,Yangzhou 225001,China)
For the rapid development and abroad application of satellite technology,it becomes an important development direction to adapt the demand of concealment attack of current high-tech battlefield to EW weapon by using satellite passive location,and the merits such as low cost and good agility of single satellite passive location system become hot points of research.This paper studies the principle and method of single satellite frequency difference passive location,puts forward the solution project aiming at the problem of location ambiguty,analyzes the factors influencing location precision and deduces the principle error and circular error probable (CEP) of location.
single satellite;passive location;frequency difference;error analysis;simulation
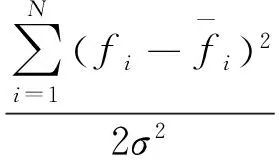
2016-08-03
TN971
A
CN32-1413(2017)02-0016-07
10.16426/j.cnki.jcdzdk.2017.02.005
