基于季节性ARIMA模型的全社会用电量预测研究
2017-06-04孙颖
孙 颖
(安徽工程大学 管理工程学院,安徽 芜湖 241000)
全社会用电量是电力市场最重要的经济指标,能够准确、及时地反映宏观经济的运行状态,与经济形势密切相关,是国民经济平稳较快发展的重要基础[1-2]。近年来,我国经济增速放缓,与此同时,作为经济状况晴雨表的全社会用电量增速也呈下降走势。
未来的全社会用电量走势如何是预测经济运行走势的重要依据。因此,科学合理地预测用电量具有重要的现实意义。本文通过分析近年来我国全社会用电量的走势及特征,建立季节性ARIMA模型并拟合检验,最后利用模型对2017年1月至2018年6月的全社会用电量进行预测。
1 理论基础
传统的依赖经验判断的弹性系数法虽简洁但精度欠缺,风险较大,不适合中长期需求预测[3],应建立需求模型来预测全社会用电量。自回归整体移动平均法(ARIMA)具有较好的适应性[4]。这一由统计学家Box和Jenkins共同提出的模型[5],能够处理非平稳时间序列的建模和预测问题[6]。
对于包含季节性变动且非平稳的序列yt,建立形如式(1)所示的ARIMA(p,d,q)(P,D,Q)S模型:
φp(L)Φp(L)(1-L)d(1-LS)Dyt=θq(L)ΘQ(L)εt
(1)
式(1)中,p是非季节自回归过程AR的阶数,q是非季节移动平均过程MA的阶数,P是季节自回归过程SAR的阶数,Q是季节移动平均过程SMA的阶数,d、Q分别是非季节差分阶数和季节差分阶数。φp(L)、Φp(L)分别是非季节自回归过程AR和季节自回归过程SAR的滞后算子多项式,(1-L)d、(1-LS)D分别是对序列yt的非季节差分和季节差分滞后算子,S是季节差分的步长,θq(L)、ΘQ(L)分别是非季节移动平均过程的MA和季节移动平均过程SMA的滞后算子多项式。
该模型的几个重要过程包括:首先,对原序列进行平稳性检验,对非平稳序列进行d阶差分变换;其次,分析序列的自相关函数和偏自相关函数,分析其是否包含季节性变动;然后,估计模型参数并诊断残差;最后,选择模型的形式并进行预测。
2 实证分析
2.1 趋势及特征分析
利用2009年9月至2016年12月数据绘制全社会用电量(TEC)序列的折线图,如图1所示。
观察图1可知,全社会用电量走势呈现季节性波动,且升中趋稳。从总量上看,整体在上升,由2009年9月的3 224亿千瓦时,到2016年12月的5 369亿千瓦时,但幅度有所减少。2009年和2010年的增速分别为6.7%和14.9%。进入2013年以后,全社会用电量增幅平稳,这主要是因为我国经济的工业主导逐渐被服务业主导所替代,而服务业对电力的需求和消费明显低于工业。2014年以来,全球经济和我国经济增长放缓。2015年受到宏观经济形势的影响,全社会用电量为55 500亿千瓦时,与2014年相比下跌3.3%,达到近年来的最低值。

图1 序列TEC的折线图
总量与增速的这种走势反映出:一方面,需求不足。宏观经济下行压力仍然存在,经济处于换挡期,工业增长速度下降,从而电力需求下降,特别是产能过剩现象较明显的钢铁、有色金属、建材等产量下降,相应的电力需求随之下降。另一方面,经济增长方式转变。服务业比重提高、传统工业转型升级等共同作用下,全社会用电量趋于平稳,这是经济新常态的特征。2016年全社会用电量为59 198亿千瓦时,同比增长5%,全社会用电量企稳回升。在经济新常态下,高耗能行业持续去产能,产业结构调整的成效已逐渐显现。随着我国工业转型升级的不断进行,用电量在一定时期内将保持平稳状态,增幅有限,也是能源利用率提高的外在表现。
2.2 数据来源及检验
2.2.1数据来源
考虑数据的可获得性,选择2009年9月至2016年12月的全社会用电量时间序列作为研究样本。其中,2009年9月至2016年6月的数据用于建模,记为序列M,2016年7月至12月的数据用于模型的拟合检验。数据全部来源于国家能源局网站。
2.2.2平稳性检验
由图1可以看出,序列M存在明显的时间趋势。选择有趋势且有截距对序列M进行单位根检验,结果如表1所示:t统计量的值-0.157 945大于检验水平1%、5%、10%的临界值,因此,拒绝原假设,认为序列M是非平稳的。

表1 序列M单位根检验结果
为了观察序列M的趋势及波动,绘制其相关图(图2)。序列M的自相关函数衰减速度非常缓慢,由此也可判断该序列是非平稳的。同时,序列的季节性很难看出,这主要是因为序列M的长期趋势掩盖了季节性。
为了更好地观察序列M的季节性,对其进行一阶自然对数差分,生成的新序列记为N。绘制序列N的相关图和Q统计量,如图3所示。
观察图3可知,序列N的自相关函数快速衰减,从而序列M的趋势基本得到消除。序列N的自相关函数在滞后1阶、6阶、12阶、24阶、36阶均超出了95%的置信区域,因此可以认为序列N存在周期为12的季节性。
为了消除季节性,对序列N做季节差分,生成的新序列记为SN。做序列SN的相关图(图4),观察图4可知,序列SN的自相关函数只在滞后1阶处显著地不为零,其他各阶滞后的自相关函数都在95%的置信区间内,由此可以判断序列M的季节性已经得到消除。

图2 序列M的自相关图
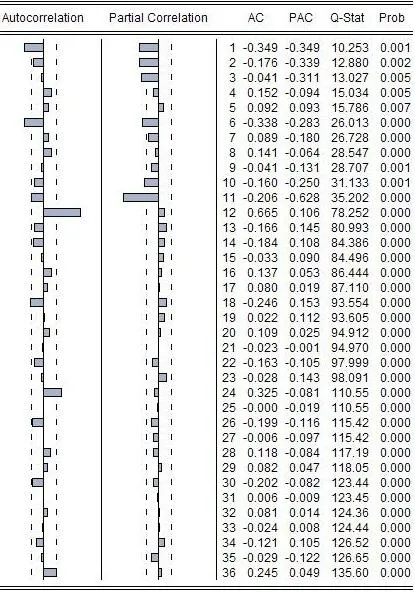
图3 序列N的相关图和Q统计量
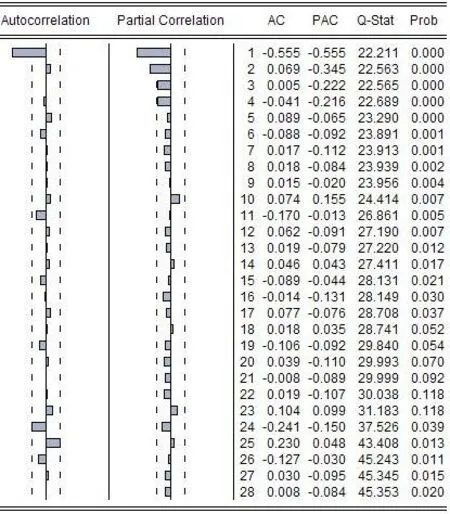
图4 序列SN的相关图和Q统计量
2.3 模型识别及检验
2.3.1模型识别
由于存在周期为12的季节性,因此,对序列M建立ARIMA(p,d,q)(P,D,Q)12模型。通过分析序列的自相关函数和偏自相关函数来识别模型的具体形式。
首先,序列M经一阶自然对数差分后趋势被消除,因此,d=1;序列M经一阶季节差分后季节性变动消除,因此,D=1;其次,由图4可知,序列SN的偏自相关函数只在滞后1阶、2阶处显著不为零,因此,p=2。序列SN的自相关函数在滞后1阶后降为零,说明MA过程是低阶的,因此,q=1。最后,由于在滞后1阶处,序列SN的自相关函数和偏自相关函数都显著地不为零,因此P=1,Q=1或为0。综上,建立ARIMA(2,1,1,)(1,1,1)12模型和ARIMA(2,1,1)(1,1,0)12模型。
2.3.2模型建立与估计
ARIMA(2,1,1)(1,1,1)12模型的估计结果如图5所示。观察分析图5的估算结果,可知AR过程和SAR过程滞后多项式的1个实数根和12个复数根,其倒数均小于1;MA过程和SMA过程滞后多项式的2个实数根,其倒数均小于1。因此,ARIMA(2,1,1)(1,1,1)12模型为平稳且可逆。
同理,得到ARIMA(2,1,1)(1,1,0)12模型的估计结果如图6所示。观察分析图6的估算结果,可知AR过程和SAR过程滞后多项式的12个实数根和1个实数根,其倒数均小于1;MA过程和SMA过程滞后多项式的1个实数根的倒数也小于1。因此,ARIMA(2,1,1)(1,1,0)12模型为平稳且可逆。

图5 ARIMA(2,1,1)(1,1,1)12模型估计结果
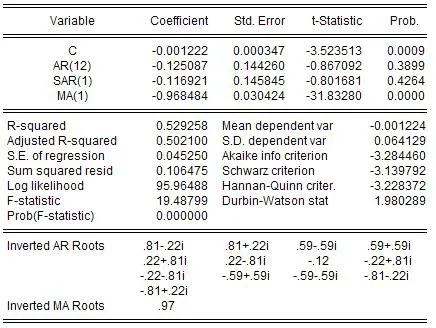
图6 ARIMA(2,1,1)(1,1,0)12模型估计结果
2.3.3残差检验
分别对两模型估计结果的残差进行白噪声检验。做两模型残差的相关图和Q统计量,分别如图7a和图7b所示。
由图7a可知,ARIMA(2,1,1)(1,1,1)12模型的估计结果的残差序列均在95%的置信区间内,且自相关函数的概率值均大于0.05,因此,可以认为ARIMA(2,1,1)(1,1,1)12模型估计结果的残差序列满足随机性假设(图7b)。同理,ARIMA(2,1,1)(1,1,1)12模型估计结果的残差序列也满足随机性假设。两模型均通过了白噪声检验。

图7a ARIMA(2,1,1)(1,1,1)12模型

图7b ARIMA(2,1,1)(1,1,0)12模型图7 两模型的残差相关图
2.3.4模型比较与选择
通过比较ARIMA(2,1,1)(1,1,1)12模型和ARIMA(2,1,1)(1,1,0)12模型的相关指标值来选择两模型中的最优者。比较结果如表2所示。

表2 两模型比较结果
2.4 模型拟合及预测
2.4.1模型拟合
利用ARIMA(2,1,1)(1,1,0)12模型对2016年7月至12月全社会用电量的月度数据对进行预测,预测值序列记为MF,结果如图8所示。
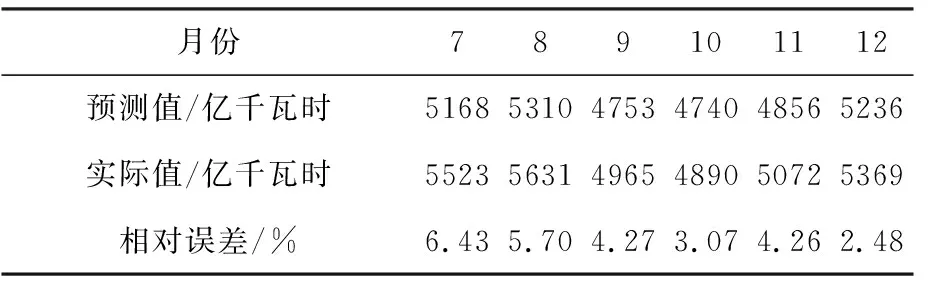
图8中,虚线是预测置信区间。将预测结果与真实值进行比较,以验证模型预测结果的可靠性和准确性。比较结果如表3所示。
由表3可知,预测值与真实值之间的相对误差较小,且误差没有随时间增大的趋势,说明ARIMA(2,1,1)(1,1,0)12模型的预测结果准确可靠,预测效果较好。

图8 2016年7月至12月的模型预测结果
月份789101112预测值/亿千瓦时516853104753474048565236实际值/亿千瓦时552356314965489050725369相对误差/%6.435.704.273.074.262.48
2.4.2数据预测
利用ARIMA(2,1,1)(1,1,0)12模型对我国2017年1月至2018年6月的全社会用电量进行预测,预测结果如图9所示。
从图9可以看出,我国全社会用电量在2017年1月以后的一年半内走势平稳,时间趋势仍然存在。将图9中的预测数据整理如表4所示。
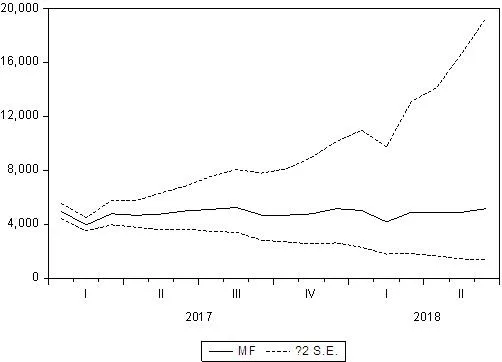
图9 2017年1月至2018年6月全社会用电量预测结果
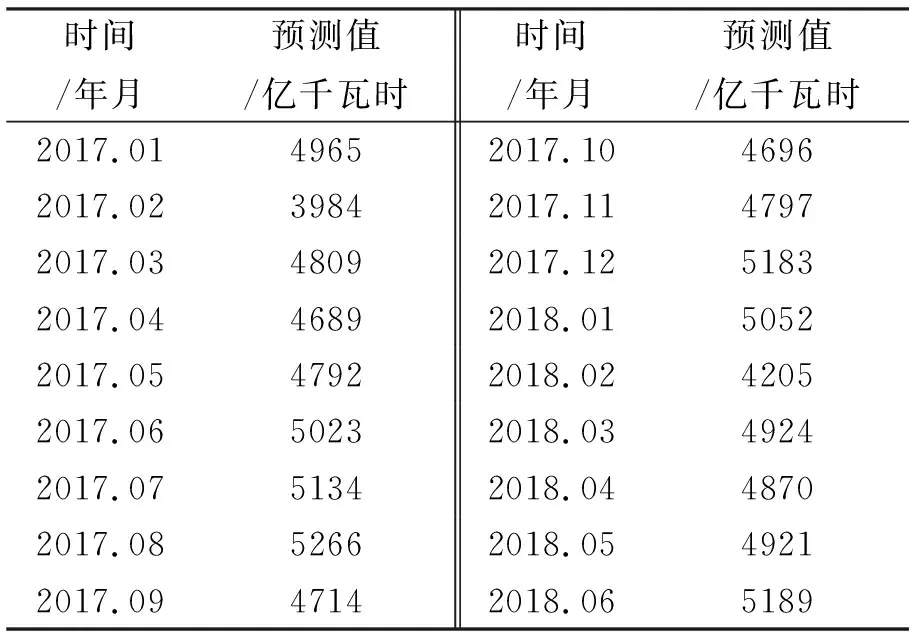
时间/年月预测值/亿千瓦时时间/年月预测值/亿千瓦时2017.0149652017.1046962017.0239842017.1147972017.0348092017.1251832017.0446892018.0150522017.0547922018.0242052017.0650232018.0349242017.0751342018.0448702017.0852662018.0549212017.0947142018.065189
3 结论及建议
选取2009年9月至2016年12月的全社会用电量数据,建立季节性ARIMA模型,并利用该模型预测2017年1月至2018年6月我国全社会用电量指标值。
实证结果表明所建立的ARIMA(2,1,1)(1,1,0)12模型为最优模型,且拟合效果较好。预测结果表明,未来半年内我国全社会用电量指标将呈波动走势,先下降后上升。这一结果说明虽然当前我国经济下行压力依然存在,但从全社会用电量指标来看,经济运行仍在合理区间内,说明经济发展的潜力和韧性较大。针对实证研究结果,为维护用电量平稳、提高能源利用率提出如下对策建议。
第一,深入推进供给侧改革。积极开展直接交易工作并扩大交易范围,拉动有效增长,增强电力市场竞争力,推进市场化改革。
第二,大力发展第三产业。第三产业的增速和趋势表明这将是未来能源消费增长的重点。同时,第三产业是节能进程中的主要贡献力量。因此,要继续提高第三产业在整个GDP中的比重。
第三,加快产业结构调整,淘汰落后产能。加快煤电结构的调整,淘汰落后产能,大力发展新能源和可再生资源,优化电力结构,促进产业链上中下游协调融合发展。
第四,强化科技创新水平,提高能源利用效率。通过强化和提升科技创新水平,推动技术的不断前进,进而降低单位能耗,提高能源利用率。
参考文献:
[1] 谭显东,胡兆光,李存斌,等.基于改进BP神经网络的全社会用电量预测模型研究[J].华北电力大学学报(自然科学版),2007,24(3):85-89.
[2] 林卫斌,陈彬,俞燕山.“十二五”及2020年电力需求预测研究[J].中国人口·资源与环境,2011,21(7):1-6.
[3] 林卫斌,苏剑,施发启.经济增长、能耗强度与电力消费用电量与GDG增长率背离的原因[J].经济科学,2010(5):15-22.
[4] Enders W. Applied Econometric Time Series[M].Wiley,New York,1996.
[5] George E P B, Gwilyn M J, Gregory C R. Time Series Analysis: Forecasting and Control[M].Wiley: New York,2015.
[6] 肖枝洪,郭明月.时间序列分析与SAS应用[M].武汉:武汉大学出版社,2009.
