时域分析法在系统响应分析中的应用

伍玩秋

（阳江职业技术学院机电系，广东阳江529500）

时域分析法在系统响应分析中的应用

伍玩秋

（阳江职业技术学院机电系，广东阳江529500）

对系统的时间响应分析是揭示系统本身动态特性的有效途径。时域分析法充分运用拉普拉斯变换（下称“拉氏变换”）规则，重视发挥数学模型的优势作用，在系统响应分析中具有独特而重要的应用。其基本思路是：运用物理规律，建立反映系统本质的微分方程；通过拉氏变换及待定系数法求出系统输入信号后的响应输出信号的拉氏变换式；利用拉氏反变换，求出系统响应输出信号的实变量函数解析式；再通过应用软件作出系统响应曲线；最后结合曲线进行必要的数学运算和推理，完成对系统有关性能的分析和总结。

时域分析法；拉普拉斯变换；系统响应；思路

1 引言

在经典控制理论中，系统时间响应是指系统在外加作用（信号输入）的激励下，其输出量随时间变化的函数关系；时域分析法通常是指直接从微分方程或间接从传递函数出发去分析系统问题的方法。时域分析法是系统时间响应分析中常用的方法，但对方法应用的一般规律却探讨得较少。本文试图以常用的单位阶跃信号为系统输入信号，以典型一阶系统（惯性环节）的时间响应分析为例，以探求时域分析法在系统响应分析中的基本思路。

2 系统微分方程的建立

【例】图1所示为惯性调节器，其中ui为输入信号，uo为输出信号，设初始条件为零。请运用时域分析法分析其单位阶跃响应输出性能。

解决问题的第一步是建立反映系统本质规律的微分方程。

根据基尔霍夫电流定律（KCL）有：

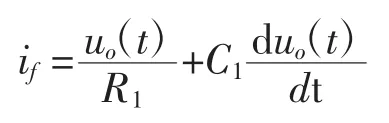
由于运算放大器的开环增益很大，这时可认为：

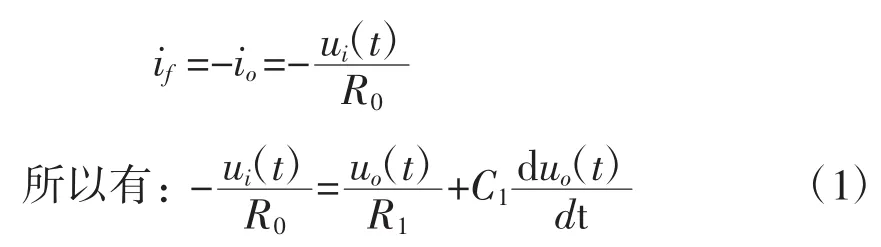
式（1）即为惯性调节器的微分方程。

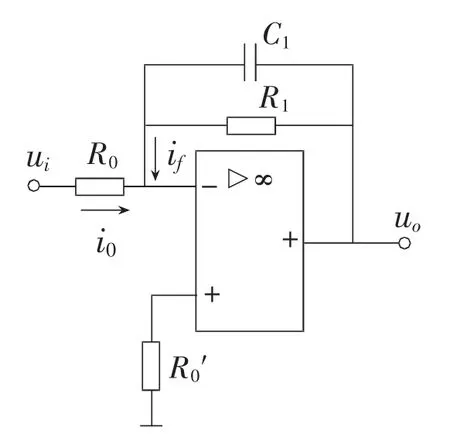
图1 惯性调节器

3 运用时域分析法进行系统响应分析的过程

3.1 求出输出信号的拉氏表达式

将系统微分方程两边进行拉氏变换：

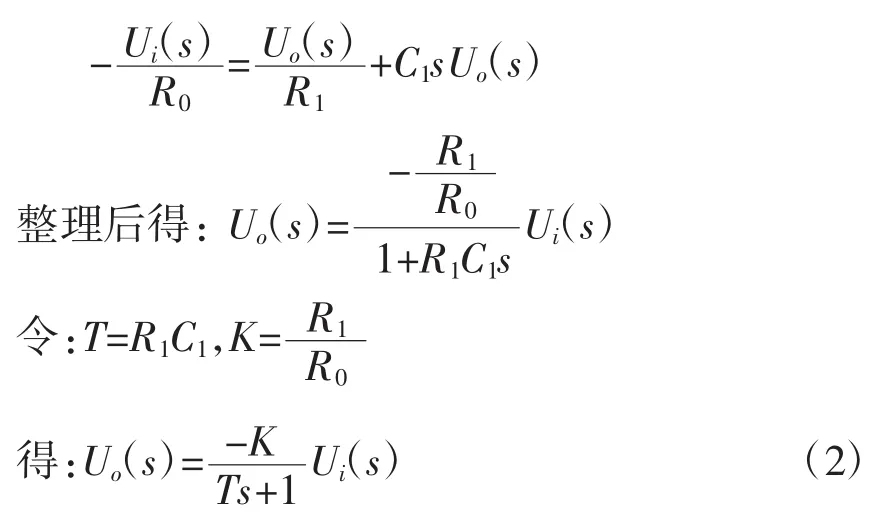
因输入信号是单位阶跃信号，且初始条件为0（即t≥1），所以ui（t）＝I（t）＝1，这时有，代入式（1）得：

式（3）即为输出信号的拉氏表达式

3.2 用待定系数法求出输出信号拉氏表达式的分式和的形式

先将式（3）变成含待定系数A、B的分式和的形式：

对比式（3）和式（4），可求得A＝1，B＝－T代入式（4）得：

3.3 通过拉氏反变换得出响应输出信号的函数解析式

根据常用函数拉氏变换对照表，将式（5）分项进行拉氏反变换，得出响应输出信号的函数解析式。

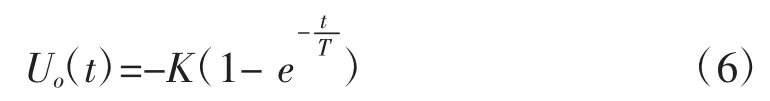
3.4 应用仿真软件（如Simulink）作出系统响应曲线

式（6）的函数图像即为惯性调节器的单位阶跃响应曲线，如图2所示。

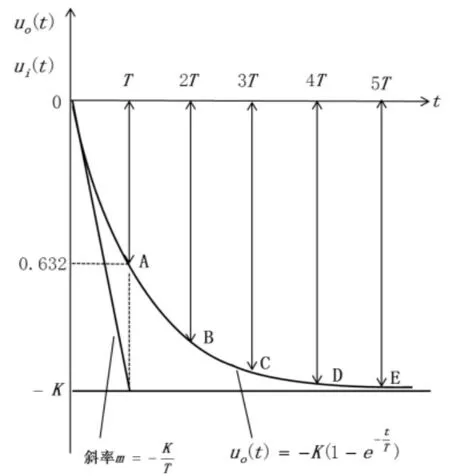
图2 惯性调节器的单位阶跃响应曲线

3.5 结合响应曲线分析系统有关性能

从上图可以看出，惯性调节器的单位阶跃响应曲线是按指数规律下降的一条曲线。该曲线有以下特征：

（1）阶跃响应曲线起点的斜率

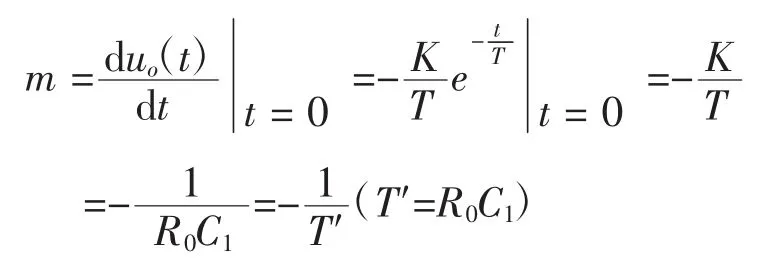
由上式可知，响应曲线起点的斜率m是时间常数T′的倒数的相反数，T′越大，m的绝对值越小，Uo（t）下降过程越慢，即Uo（t）的绝对值上升过程越慢。

（2）稳态值

Uo（t）的稳态值为

（3）趋向稳态值的过渡时间

由曲线可知，在t经过T、2T、3T、4T、5T后，其响应输出值分别为稳态值的63.2%、86.5%、95%、98.2%、99.3%。由此可见，对典型一阶系统，其过渡时间大约为（3－5）T，响应输出值可达到稳态值的95%－99.3%。

4 结束语

综上可知，时域分析法在系统响应分析中的基本思路是：运用物理规律，建立反映系统本质的微分方程；通过拉氏变换、待定系数法及拉氏反变换，求出系统响应输出实变量函数解析式；通过应用软件做出系统的响应曲线，最后结合曲线对系统进行必要的数学运算和推理，完成对系统有关性能的分析和总结。在此过程中，拉氏变换和拉氏反变换规则、常用数学模型及待定系数法等数学工具的运用，使求解过程变得简单、有效；系统仿真软件的运用使系统响应曲线的绘制变得更为方便、真实。尽管以上方法及思路是通过典型一阶系统（惯性环节）的阶跃响应分析总结出来的，但对其他二阶以上系统的响应分析同样具有普遍的借鉴意义。

［1］孔凡才.自动控制原理与系统（第3版）［M］.北京：机械工业出版社，2016：18－57.

［2］冯士伟，李 勇，武志忠，张沛勇.一种一阶延迟惯性环节温控系统优化设计方法［J］.空间控制技术与应用，2015（02）：41－45.

［3］骆 建，谢 榕.时域分析法的教学难点及应对方法［J］.电气电子教学学报，2015（2）：54－57.

［4］李华川，张群生.空气轴承式板形仪对单位阶跃信号的动态响应分析［J］.机械工程与自动化，2010（04）：16－18.

［5］王荔芳，周晓华，陶燕林.基于Simulink的自动控制系统性能的分析与仿真［J］.现代电子技术，2010（22）：126－127.

［6］刘海波，杨海柱.MATLAB仿真在自动控制系统实验教学中的应用［J］.中国电力教育，2012（13）：99－101.

［7］潘湘高，杨民生，敖章洪.MATLAB在控制系统时域分析中的应用［J］.湖南文理学院学报（自然科学版），2016（03）：83－87＋91.

［8］汪 建.用时域分析法求解冲激响应的方法［J］.电气电子教学学报，2011（06）：103－105.

Application of time domain analysis method in system response analysis

WU Wan－qiu
（Yangjiang Vocational and Technical College，Yangjiang 529500，China）

The time response analysis of the system is an effective way to reveal the dynamic characteristics of the system itself.The time domain analysis method，which is based on the Laplace transform rule and takes advantage of the mathematical model，has a unique and important application in the system response analysis.The basic ideas in the analysis process are the following：to established the differential equation by the physical laws to reflect the essence of the system；to calculate the Laplace transform of the response output signal after the input signal by the Laplace transform method and the undetermined coefficient method；to calculate the system response functional analysis of the real－time variable－type output signal by using the inverse Laplace transform；to draw the system response curve by the software application；to do some mathematical calculations and some necessary reasoning by curves；to complete the analysis and summary for the performance of the system.

time domain analysis method；Laplace transform；system response；ideas and solutions

TM131

：A

1005—7277（2017）01—0058—03

伍玩秋（1967－），男，硕士，高级工程师，主要从事电气自动化相关课程教学及技术研究工作。

2016－10－09