基于OpenSees的钢筋混凝土剪力墙数值分析
2017-06-01余欣张爱社
余欣,张爱社
(山东建筑大学土木工程学院,山东济南250101)
基于OpenSees的钢筋混凝土剪力墙数值分析
余欣,张爱社*
(山东建筑大学土木工程学院,山东济南250101)
有限元数值模拟是研究钢筋混凝土剪力墙抗震性能的一种有效手段,不同数值分析模型的选取对钢筋混凝土剪力墙抗震性能的研究有较大的影响。文章通过OpenSees软件分别采用基于塑性铰单元的纤维模型和基于位移的纤维单元对不同轴压比下钢筋混凝土剪力墙建立了数值分析模型,分析材料的本构模型,阐述不同轴压比的钢筋混凝土剪力墙低周反复荷载试验,并将数值模拟结果与试验结果进行对比分析。结果表明:钢筋混凝土剪力墙由弯曲变形控制、滞回环比较饱满、耗能情况比较好、具有较好的抗震性能,同时随着轴压比的增大,试件的屈服荷载和极限荷载都有显著增加,延性系数有所降低;采用基于塑性铰单元的纤维模型在合理确定塑性区段范围的基础上能够更好的模拟以受弯为主的钢筋混凝土剪力墙的抗震性能;基于塑性铰单元模拟得到的屈服荷载值、极限荷载值以及延性系数与试验结果的误差都控制在10%之内,而基于位移的纤维单元模拟得到的屈服荷载值误差都超过20%、极限荷载值误差在10%之内。
OpenSees;钢筋混凝土剪力墙;纤维模型;抗震性能
Key words:OpenSees;reinforced concrete shear wall;fibermodel;seismic performance
0 引言
利用有限元方法对钢筋混凝土剪力墙进行相关的数值模拟分析是学术研究中的一种有效方式。由于钢筋混凝土剪力墙构件的几何尺寸和板壳单元类似,厚度方向的尺寸远远小于高度和宽度方向的尺寸。因此,采用板壳单元模拟钢筋混凝土剪力墙构件受力特性最为精确。但是采用板壳单元会极大增加模型的计算量,特别是对整体结构进行动力弹塑性分析的时候[1]。为了更好的解决计算量大的问题,很多学者提出符合钢筋混凝土剪力墙受力特性的宏观模型(如等效梁柱单元模型、三垂直杆模型(TVLEM)、多垂直杆模型(MVLEM)、纤维模型、分层壳模型等)[2-5]。纤维模型从材料特性和截面配筋布置出发,将构件截面细分成很多小的纤维束。不同纤维束之间服从平截面假定和位移协调条件,考虑了轴力和弯矩的相互关系,同时截面上不同的纤维可以赋予不同的材料本构关系,所以纤维单元能够较好地模拟以受弯为主的结构。再加上宏观模型在满足模拟精度的前提下具有计算量小、自由度少、成本低的特点,使其无论在构件模拟或者整体结构的模拟中都有较大的优势。目前陈学伟开发了基于纤维单元的结构弹塑性分析软件平台MESAP,并对钢筋混凝土柱低周往复试验进行数值模拟[6];宁列超用三种非线性梁柱单元模拟一个钢筋混凝土柱构件并指出这三种非线性梁柱单元对于截面软化行为各自所具有的优势与不足[7];李宁波应用OpenSees计算双钢管高强砼柱的滞回曲线[8]。童小龙采用分层壳单元对活性粉末混凝土剪力墙进行了非线性分析及轴压比限值的研究[9];童师敏采用基于位移的纤维单元模拟了双钢板高强混凝土组合剪力墙[10];潘志宏基于OpenSees平台提出了开洞混凝土墙体静力非线性分析的方法及其实现技术[11]。上述研究都是基于OpenSees软件对各种构件和模型进行了分析和描述,但对于采用Displacement-Based Beam-Column单元和Beam With Hinges单元的纤维模型在模拟钢筋混凝土剪力墙时一些具体数值模拟分析过程并没有解释清楚,针对这一情况文章运用OpenSees软件,基于纤维模型分别采用Displacement-Based Beam-Column单元和Beam With Hinges单元对2片不同轴压比的钢筋混凝土剪力墙进行了数值模拟,详细说明了截面纤维的划分、两种纤维单元的优缺点、本构模型的选取及相关参数的设定,并与钢筋混凝土剪力墙低周反复加载试验结果进行对比验证。
1 剪力墙数值分析模型
OpenSees软件中的纤维模型是将钢筋混凝土剪力墙中的钢筋和混凝土分别划分成若干离散纤维束,然后用相对应的钢筋、混凝土本构关系来反应纤维束的力学特性。所以纤维模型可以很好地模拟不同截面形状构件的力学性能,也可以同时考虑轴力和弯矩的相互关系,理论上有较高的精度[12]。
1.1 基本假定
纤维梁柱单元的计算公式基于线性几何的假定。由于钢筋混凝土材料的非均匀质性,所以可能存在裂缝,严格来说,平截面假定不成立。因为平截面在单元变形历史中保持为平面并与纵轴垂直,这种假设对于由均质材料组成的单元发生小变形的情况是可以接受的,而用来解释钢筋混凝土单元一些特征现象比如开裂和粘结滑移是不合理的,但大量试验结果表明,沿构件轴线取出一段长度的平均应变在构件截面上的分布仍然基本符合平截面假定[13]。根据有限元分析的弥散裂缝概念,开裂影响和受拉刚度可以通过对预应力钢筋或钢筋混凝土的应力应变关系的适当修改而被包含在模型中,这种影响只在发生屈服阶段前的响应中是明显的,在发生较大非弹性变形产生滞回性能的研究中可以被忽略。相反,粘结滑移对单元变形的贡献随着荷载幅值和循环次数增加而更加明显。对于受弯为主的剪力墙构件来说由于剪切效应所占比重很小剪力效应可以被忽略,所以这对于高宽比比值在2以上的构件是一种合理的近似。
1.2 纤维单元
1.2.1 Displacement-Based Beam-Column单元
Mari等在1984年提出了基于位移的梁柱单元模型[14],同时对刚体位移向量有了明确的规定,如图1所示。

图1 刚体位移向量规定示意图
该模型在单元的长度方向上划分为若干个积分区段,积分点处截面的位移计算都是通过3次Hermit多项式插值得到。截面变形d(x)通过对插值函数进行求导得到,由式(1)、(2)表示为
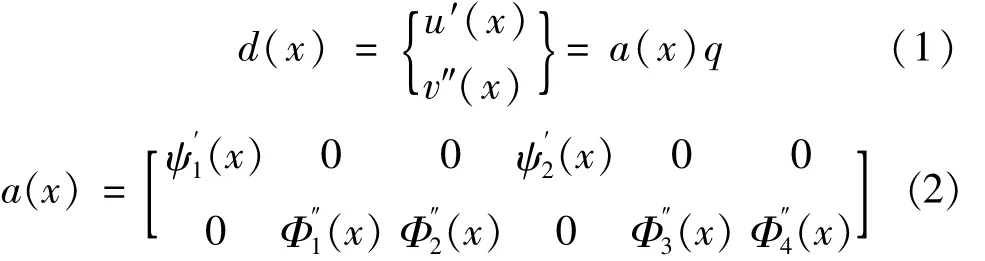
式中:u′(x)为轴向应变;v″(x)为曲率;a(x)为插值函数求导值;q为节点位移矩阵;ψ′i(x)(i=1,2)为横向位移插值函数的一阶导数;Ф″j(x)(j=1,2,3,4)为纵向位移插值函数的二阶导数。
其次,通过截面变形与截面的力—位移关系得到截面抗力向量与切线刚度矩阵,截面的刚度矩阵k(x)沿长度进行积分得到单元刚度矩阵K,由式(3)表示为
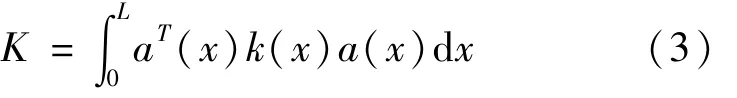
最后对截面的抗力DR(x)沿长度进行积分得到单元抗力QR,由式(4)表示为
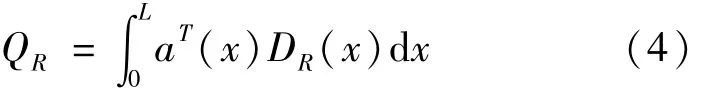
从以上的求解方法可以看出,基于位移的纤维单元主要劣势是插值函数不能很好描述纤维端部屈服后单元的曲率分布情况,而且在单元层次上不能迭代计算,因此收敛速度慢。所以为减少插值函数造成的误差,一般都采用增加单元划分数量的方式来保证模拟得到的结果的准确性。
1.2.2 Beam With Hinges单元
塑性铰模型是常用的纤维模型,其优点是采用简单的截面力—位移关系曲线或者采用纤维截面的方式来表达复杂的构件弹塑性行为。基于塑性铰的纤维单元与基于柔度法的纤维梁柱单元是类似的,两者的计算过程相同,都具有单元内迭代的步骤,不同之处在于塑性铰单元的两端为塑性区段中间部分为弹性区段,不需要和基于柔度法的纤维梁柱单元一样求解切线刚度与截面抗力,只要塑性区截面收敛,单元内部迭代就收敛,这样在计算过程中减少了大量的迭代计算步骤,从而提高了单元的求解效率。塑性铰单元的柔度矩阵F求解由式(5)表示为
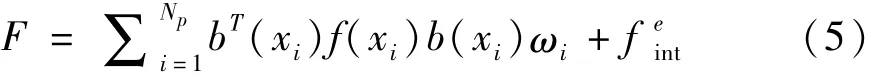
式中:f(xi)为截面柔度矩阵;b(xi)为力差值函数矩阵;ωi为权重系数;feint为弹性部分的柔度矩阵,计算公式由式(6)、(7)表示为

式中:E为弹性模量,N/mm2;I为截面惯性矩,mm4;A为截面面积,mm2。
Scott等给出了塑性铰单元常用的4种积分方式,分别为两端端中点积分法,两端边点积分法,两端Gauss-Radau积分法以及修正的Gauss-Radau积分法[15],积分法的示意图如图2所示。其中,修正的Gauss-Radau积分法的第2个与第3个积分点属于弹性部分,虽然采用的是四点积分,但实际需要进行截面分析的只有2个积分点,所以它的弹性部分柔度矩阵需要改写,改写后的柔度矩阵由式(8)表示为
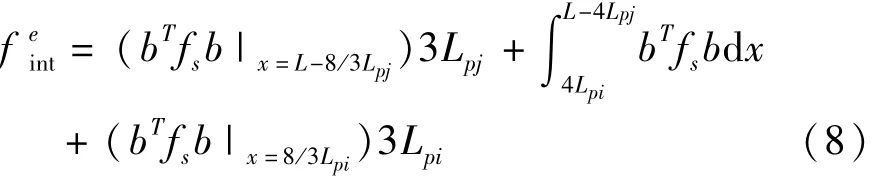
式中:Lpi、Lpj分别为单元左右端塑性区长度,mm。

图2 塑性铰单元积分形式示意图
根据图2可以看出,由于需要进行四个积分点处的截面分析,所以两端Gauss-Radau积分法计算量较大,效率较低。选取修正的Gauss-Radau积分法,同时根据Priestley等提出的塑性区长度Lp的计算公式确定塑性区长度[16],由式(9)表示为
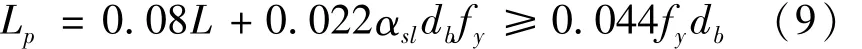
式中:αsl为钢筋滑移参数,考虑钢筋滑移时,αsl=1;不考虑钢筋滑移时,取αsl=0;fy为钢筋屈服强度,MPa;db为钢筋直径,mm;L为构件长度,mm。
1.3 截面纤维划分
截面各部分的纤维数量通常根据分析需要及构件复杂程度而定,截面纤维量越大,越接近实际情况,但相应的计算时间越长,分析效率降低。将剪力墙模型沿高度方向划分为4个单元进行模拟;混凝土保护层部分在截面宽度方向划分3层纤维、截面高度方向划分18层纤维;两侧暗柱在截面高度方向划分5层纤维;中间混凝土部分划分9层纤维,具体截面纤维划分如图3所示。

图3 剪力墙截面纤维划分图
1.4 模型求解与输出
OpenSees在求解模块中提供了多种外荷载控制方法以及内部矩阵的求解算法。为了与试验加载方式统一,在OpenSees软件中通过“sp*”命令来实现位移控制的加载方式,求解时选用Krylov-Newton算法进行求解。同时对结构的受力特性进行全面的分析时,OpenSees软件提供了各种分析数据的输出选项,包括各结点的位移、速度、加速度,不同坐标系下单元任一单元截面的内力、变形、刚度以及整个分析过程中结点响应的包络值。采用纤维截面建立单元时,还可以输出任意纤维束的应力应变数据。为了得到试件的滞回曲线,通过软件中的“Recorder Node Disp*”、“Recorder Node Reaction*”命令分别输出的试件的顶点位移和基底剪力,并用绘图软件Origin进行数据处理,得到对比分析所需的滞回曲线图和骨架曲线图。
2 材料本构模型
2.1 钢筋材料本构模型

图4 钢筋本构模型图
钢筋本构采用Steel02模型,如图4所示,最初由Menegotto和Pinto(1973)提出[17],后来经过Flilppou等的修正,其骨架曲线为双折线[18]。该模型能较好地考虑各向同性应变硬化对钢筋受力性能的影响,同时也考虑了Bauschinger效应。其中控制本构模型由弹性到塑性的参数采用本构模型默认值,即R0=20,CR1=0.925,CR2=0.15。
2.2 混凝土材料本构模型
混凝土本构采用Concrete02模型[19],如图5所示。该模型为修正的Kent-Park模型,考虑混凝土的受拉作用,单轴受拉按线性软化考虑,同时也考虑了箍筋对约束区混凝土强度及延性的提高。本构受压区曲线分为上升段、下降段及平台段,由式(10)、(11)、(12)表示。
当εc≤ε0时
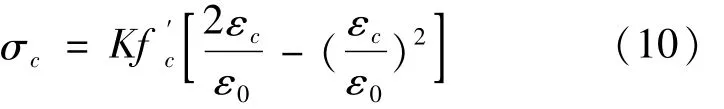
当ε0<εc≤ε20时

当εc>ε20时

式中:

式中:ε0为混凝土应力峰值时的压应变;εc为混凝土的压应变;σc为混凝土压应变为εc对应的压应力;ε20为混凝土应力下降至20%峰值应力时对应的压应变;K为箍筋对混凝土强度提高系数;Zm为应变软化率系数;f′c为混凝土圆柱体抗压强度,MPa;fyh为箍筋的屈服强度,MPa;ρs为体积配箍率;h′为箍筋肢距,mm;sh为箍筋间距,mm。
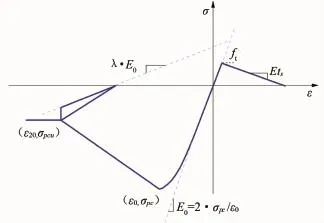
图5 混凝土本构模型图
模型中约束混凝土和非约束混凝土本构参数均按照上述公式计算取值。
3 模拟与试验结果对比分析
3.1 剪力墙低周反复加载试验
3.1.1 试件设计
设计2片不同轴压比的现浇剪力墙进行低周反复加载试验,其中轴压比为0.1的编号为SW-1、轴压比为0.3的编号为SW-2。钢筋混凝土剪力墙墙肢的高度、厚度和宽度分别为3200、150、1200 mm,试件截面配筋图如图6所示。

图6 剪力墙截面配筋图/mm
墙体及加载梁均采用C30的自密实混凝土,地梁采用的是C40商品混凝土,同时所有试件均采用HRB400级钢筋,实测的混凝土和钢筋的力学性能分别见表1、2。

表1 混凝土力学性能

表2 钢筋力学性能
3.1.2 试验加载方案及数据采集
试验时先在剪力墙顶部按照设计的轴压比施加轴压,然后在剪力墙水平方向进行低周往复加载试验。试验过程中,水平荷载采用位移控制方法,采用逐级增加位移的方式反复加载,为了保证反复加载的连续性和均匀性,以及加载和卸载时速度的一致性。试验加载至试件破坏或荷载下降至最大荷载的85%左右时停止试验。
为了更加全面的获取试验过程中的数据,试验中布置了多种荷载、位移等传感器,用以记录试件的各项反应,如位移、荷载、钢筋应变,同时安排相关人员进行墙体裂缝等其他破坏现象的记录。
3.1.3 试验现象及结果
剪力墙SW-1、SW-2的滞回曲线及破坏形态分别如图7、8所示。由图7、8可以看出试件以弯曲变形为主,滞回环比较饱满,屈服后构件刚度衰减不严重,表明钢筋混凝土剪力墙延性和耗能都较好,具有良好的抗震性能。对于剪力墙SW-1,当位移加载到8 mm,荷载为208.7 kN时,在剪力墙的左侧受拉区开始出现水平裂缝;位移加载到18 mm时,荷载为279.8 kN时,剪力墙的右侧开始处出现斜裂缝,角度约为45°。此后随着位移继续增加,荷载增速明显减慢,构件不断出现新的水平裂缝和斜裂缝,裂缝宽度不断增大,裂缝长度不断向中部延伸。当位移达到35 mm时,剪力墙两侧角部的混凝土开始开裂剥落;当位移加载到70 mm时剪力墙右下端混凝土成片脱落,纵筋外露、压屈。继续加载时,压屈后的从筋被拉断,混凝土的水平裂缝由墙角向中部腹板延伸,试件承载力急剧下降,试验停止。
剪力墙SW-2,当位移加载到9 mm,荷载为216.3 kN时,在剪力墙的左侧受拉区开始出现水平裂缝;位移加载到11 mm,荷载为249.8 kN时,剪力墙的右侧开始处出现沿着约45°方向的斜裂缝。此时随着位移的增加荷载增速明显减慢,剪力墙中下部不断出现新的水平裂缝和斜裂缝,并不断延伸。裂缝宽度也随着位移的增加而不断增大。当位移达到37 mm时,剪力墙两侧角部的混凝土开始剥落,当位移加载到69 mm时剪力墙角部两端混凝土成片脱落,纵筋外露、压屈。继续加载时,压屈后的纵筋被拉断,混凝土的水平裂缝由墙角向中部腹板延伸,试件承载力急剧下降,试验停止。对比两个试件的试验数据及破坏形态图可以发现:随着轴压比的增大试件的极限承载力有明显的提高、剪力墙的塑性变形能力有所减小;同时可以发现2片剪力墙裂缝的主要发展区域集中在墙体2 m以下部分,混凝土剥落区域主要集中在墙体根部250 mm区段内。
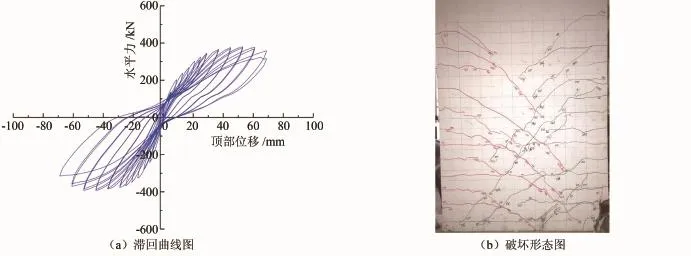
图7 剪力墙SW-1滞回曲线及破坏形态图

图8 剪力墙SW-2滞回曲线及破坏形态图
3.2 模拟与试验结果对比分析
基于OpenSees软件采用Displacement-Based Beam-Column单元和Beam With Hinges单元模拟钢筋混凝土剪力墙得到的滞回曲线、骨架曲线分别与试验得到的滞回曲线、骨架曲线相对比如图9、10所示。
由图9(b)、(d)和图10可以看出基于塑性铰单元模拟的不同轴压比的钢筋混凝土剪力墙得到的滞回曲线、骨架曲线与试验相比无论结构的初始刚度、加卸载曲线、滞回环面积、极限承载力以及延性方面都有很高的吻合度,滞回曲线的捏拢程度也很一致,表明模型中采用基于塑性铰的纤维单元依据Priestley等提出的塑性区长度Lp的计算公式合理地确定了塑性区段的范围,能够很好地模拟钢筋混凝土剪力墙底部塑性区段内的刚度退化以及显著的非线性特征,所以模拟结果能够很好地与试验结果相吻合。图9(a)、(c)和图10可以看出基于位移的单元模拟的与试验相比高估了结构的初始刚度、极限承载力以及延性,同时滞回环也更加饱满,这是因为基于位移的纤维单元不能很好地描述单元接近其极限强度和应变软化开始后的响应,再加上假设的3次Hermit插值函数不能很好的描述端部屈服单元的曲率分布,所以当钢筋混凝土剪力墙底部钢筋和混凝土产生明显的屈服变形时,单元不能很好的模拟出塑性区端内材料显著地非线性特点,造成模拟结果出现较大的误差。
一般对于数值模拟精准度都是通过对比试件滞回曲线、骨架曲线的特征值来确定。选取屈服荷载、极限荷载以及延性系数三个方面进行对比,具体模拟与试验特征值对比结果见表3。表中Py代表试验的屈服荷载值;Py1代表基于位移纤维单元的屈服荷载值;Py2代表基于塑性铰单元的屈服荷载值;Pu代表试验的极限荷载值;Pu1代表基于位移纤维单元的极限荷载值;Pu2代表基于塑性铰单元的极限荷载值;μ代表试验的延性系数;μ1、μ2分别代表基于位移纤维单元和基于塑性铰单元的延性系数;ω1、ω2分别代表基于位移纤维单元和基于塑性铰单元与试验值的误差,计算公式为误差 =(模拟值 -试验值)/试验值。

图9 模拟与试验滞回曲线对比图
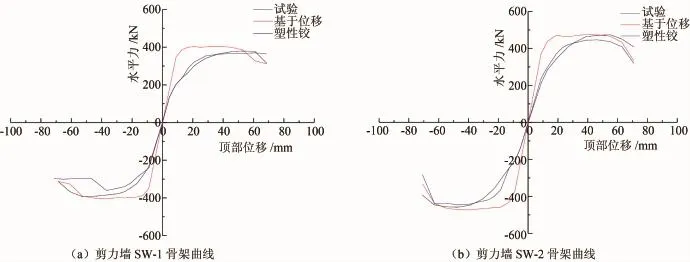
图10 模拟与试验骨架曲线对比图

表3 模拟与试验特征值对比
根据表3可以看出对于不同轴压比的试件,基于塑性铰单元模拟得到的屈服荷载值、极限荷载值以及延性系数误差都控制在10%之内,具有较好的精度;基于位移的纤维单元模拟得到的屈服荷载值误差都超过20%、极限荷载值误差在10%之内,延性系数误差也较大;同时随着轴压比的增大,试件的屈服荷载、极限荷载都有较明显的提升,位移延性系数有所减小。
4 结论
通过上述研究表明:
(1)钢筋混凝土剪力墙由弯曲变形控制,滞回环比较饱满,屈服后构件刚度衰减不严重,表明钢筋混凝土剪力墙延性和耗能都较好,具有良好的抗震性能。同时,随着轴压比的增大,试件的屈服荷载和极限荷载都有显著增加,延性系数有所降低。
(2)采用基于塑性铰单元的纤维模型采用文中划分单元的方式,相关参数的选取以及塑性区段的范围确定按照文中建议的相关公式计算取值后能够较好的模拟以受弯为主的钢筋混凝土剪力墙的抗震性能。
(3)基于塑性铰单元模拟得到的屈服荷载值、极限荷载值以及延性系数与试验结果的误差都控制在10%之内,具有较高的精度,能够很好地模拟出剪力墙结构的受力性能;基于位移的纤维单元模拟得到的屈服荷载值误差都超过20%、极限荷载值误差在10%之内,能模拟出构件受力的变化趋势。
[1] 缪志伟.钢筋混凝土框架剪力墙结构基于能量抗震设计方法研究[M].北京:中国建筑工业出版社,2014.
[2] 江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005.
[3] Kabeyasawa T.,Shiohara H.,Otani S.,et al..Analysis of the Full-Scale seven story reinforced concrete test structure[J]. Journal of the Faculty of Engineering,1983,37(2):432-478.
[4] Orakcal K.,Wallace J.W.,Conte J.P..Nonlinearmodeling and analysis of slender reinforced concrete walls[J].American Certification Institute Structural Journal,2004,101(5):688-698.
[5] 解琳琳,黄羽立,陆新征,等.基于OpenSees的RC框架-核心筒超高层建筑抗震弹塑性分析[J].工程力学,2014,31(1):64-71.
[6] 陈学伟,韩小雷,孙思为.三种非线性梁柱单元的研究及单元开发[J].工程力学,2011,28(S1):5-11.
[7] 宁超列,段忠东.OpenSees中三种非线性梁柱单元的研究[J].低温建筑技术,2009,31(3):49-52.
[8] 李宁波,钱稼茹,纪晓东,等.应用OpenSees计算双钢管高强砼柱的水平力-位移滞回曲线[J].防灾减灾工程学报,2014,34(5):606-612.
[9] 童小龙,方志,罗肖,等.RPC剪力墙非线性分析及轴压比限值研究[J].四川大学学报(工程科学版),2015,47(4):45-51.
[10]童师敏,陈麟,周云.双钢板高强混凝土组合剪力墙滞回性能模拟[J].华南地震,2014,34(z1):102-106.
[11]潘志宏,李爱群.混凝土剪力墙结构静力非线性分析的弯剪模型及实现[J].东南大学学报(自然科学版),2012,42(4):701-705.
[12]梁兴文,叶艳霞.混凝土结构非线性分析[M].北京:中国建筑工业出版社,2007.
[13]江见鲸,李杰,金良伟.高等混凝土结构理论[M].北京:中国建筑工业出版社,2006.
[14]Mari A.,ScordelisA..Nonlinear Geometric Material and Time Dependent Analysis of Three Dimensional Reinforced and PrestressedConcrete Frames[R].Berkeley:Department of Civil Engineering,University of California,1984.
[15]ScottM.H.,Fenves G.L..Plastic hinge integrationmethods for force-based beam-column elements[J].Journal of Structural Engineering,2006,132(2):244-252.
[16]Priestley M.J.N.,Seible F.,CalviG.M.S..Seismic Design and Retrofit of Bridges[M].New York:John Wiley&Sons,1996.
[17]Menegotto M..Method of Analysis for Cyclically Loaded R.C. Plane Frames Including Changes in Geometry and Non-Elastic Behavior of Elements under Combined Normal Force and Bending[C].Zurich:International Association for Bridge and Structural Engineering,1973.
[18]Filippou F.C.,Popov E.P.,BerteroV.V..Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints[R].Berkeley:Earthquake Reserch Center,University of California,1983.
[19]Scott B.D.,Park R.and Priestley M.J.N..Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J].American Certification Institude Structural Journal,1982,79(2):13-27.
Numerical analysis of reinforced concrete shear wall based on OpenSees
Yu Xin,Zhang Aishe*
(School of Civil Engineering,Shandong Jianzhu University,Jinan 250101,China)
The finite element numerical simulation is an effective method to study the seismic performance of reinforced concrete shear wall,and the selection of different numerical analysismodel has a great influence on the seismic performance of reinforced concrete shear wall.The finite element software OpenSees is used to establish the numerical analysismodel of reinforced concrete shear wall under different axial compression ratios,the fibermodels based on the beam with hinges element and the displacement based on beam column element are simulated respectively.Meanwhile,the constitutivemodel ofmaterial is analyzed,the low cyclic loading test of reinforced concrete shearwall is presented,and the simulation results are compared with the test results.The results indicate that the reinforced concrete shear wall is controlled by flexural deformation,the hysteresis loop is full,the energy consumption is better and has better seismic performance.With the increase of axial compression ratio,the yield load and ultimate load of the specimens increase significantly,and the ductility coefficient decreases a little.The fiber model based on the beam with hinges element can better simulate the seismic performance of the reinforced concrete shear wall when the plastic section is determined reasonably.The error of the yield load,ultimate load and the ductility coefficient based on the beam with hinges element is controlled within 10%.The error of the yield load is over 20% and the error of the ultimate load is controlled within 10%,which are based on the Displacement-Based Beam-Column Element.
TU317.1;TU398.2
:A
1673-7644(2017)02-0144-08
2017-03-20
国家自然科学基金项目(51078225)
余欣(1993-),男,在读硕士,主要从事结构抗震等方面的研究.E-mail:yuxin1993@icloud.com
*:张爱社(1969-),男,教授,博士,主要从事混凝土结构抗震等方面的研究.E-mail:sdjzutmsys@163.com
