变截面刚构桥主梁几何参数统计分析
2017-06-01徐刚年王有志安然袁泉尤伟杰张涛王来永武俊彦
徐刚年,王有志,*,安然,袁泉,尤伟杰,张涛,王来永,武俊彦
(1.山东大学土建与水利学院,山东济南250061;2.交通运输部公路科学研究院,北京100088)
变截面刚构桥主梁几何参数统计分析
徐刚年1,王有志1,*,安然1,袁泉1,尤伟杰1,张涛1,王来永2,武俊彦2
(1.山东大学土建与水利学院,山东济南250061;2.交通运输部公路科学研究院,北京100088)
主梁几何参数的取值及内在规律研究可为桥梁设计人员提供参考依据。通过收集国内外已建三跨变截面刚构桥数据,采用最小二乘法回归分析了边中跨比、梁高跨比、箱梁壁厚跨比、顶底板宽比、墩顶与跨中腹板厚度参数随最大跨径或建成时间的变化关系。结果表明:国内边跨比选取范围趋向于0.53~0.55之间,与1989~2005年期间的0.56~0.63存在巨大差异,且与最大跨径无明显的相关性;跨径超过200 m的桥梁跨中腹板厚度在40~50 cm之间,平均值较1989~2005年期间有所减小;墩顶、跨中梁高比在1/15.4~1/18.1和1/42~1/58之间,较1989~2005年期间均有提高,国内墩顶梁高比随最大跨径的增大而增大,但国外则相反;顶底板宽比平均值为1.83,小于1994~2005年期间的1.94,且与最大跨径无相关性;墩顶、跨中腹板厚度参数均偏离最佳腹板厚度参数,且跨中偏离较大,1988~2005年期间墩顶腹板厚度参数与最佳腹板厚度参数较为吻合。
变截面刚构桥;主梁几何参数;最小二乘法;回归分析
0 引言
预应力混凝土刚构桥具有结构刚度大、变形小、行车平顺舒适、经济适用、养护简单等优点,其在公路桥梁中广泛采用。截止2016年6月,我国已建单孔最大跨径≥40 m的预应力混凝土连续T梁或箱梁桥共3713座,目前已在国内公路桥梁交通建设中得到广泛应用。近20年的桥梁普查和养护中,许多大跨径预应力混凝土箱梁桥普遍出现箱梁开裂和跨中下挠[1-2],且两种病害均随时间延续不断发展,相互影响,甚至导致桥梁坍塌。预应力混凝土变截面刚构桥主桥几何设计参数选取在初步设计中均占有十分重要的地位,直接影响桥梁的安全性和耐久性。早期在役桥梁由于跨径的比例选择不当、箱梁腹板厚度选取不佳、变截面梁高设置不合理及单箱室大挑臂的薄壁结构的使用,是造成病害的原因之一。近年来,随着人们对桥梁轻型美观的要求越来越高,大跨径预应力混凝土刚构桥主桥的结构尺寸设计也逐渐偏离了结构本身的力学要求[3-4]。因此,选择合理的主梁几何参数,是设计关键。
通过在役预应力混凝土变截面刚构桥资料收集和分析,国内外学者主要探讨了主梁几何参数与混凝土梁体开裂关系,或者运用不同优化方法给出参数选取值,或者结合工程实例设置关键参数特定值对整桥进行数值模拟分析,优化主梁设计参数[5-7]。预应力混凝土变截面刚构桥主梁几何参数的研究取得了一定成果。但是,目前研究主要集中在某座新建桥梁中某个或者某几个几何参数的优化,或者选取不同跨径数目的在役桥梁进行统计分析,按桥梁类别、特定的跨径数目和时间段进行几何参数统计分析未见相关报道。文章按2个时间段对国内外公路跨径大于或等于100 m三跨变截面刚构桥主桥的边跨比、高跨比、厚跨比以及顶底板宽比等参数进行数据统计研究,探讨主梁几何参数的取值范围,分析某些桥梁几何参数偏离常规取值范围的原因,总结关键几何参数的变化规律及相关经验公式。
1 线性回归分析模型
假设有数据集(x1,y1)、(x2,y2)、…、(xm,ym)(xi,yi∈R;i=1,2,…m,m∈N),描述这些数据最简单的方法是运用由式(1)表示的模型函数为

式中:x为解释变量;^y为响应变量;a、b为回归系数。
如果偏差yi-^y(x)(i=1,2,…,m)足够小,则式(1)与数据拟合较好,由式(2)表示的残差平方和RSQ为

为使数据与模型之间偏差较小,需要使RSQ值较小。在回归过程中,通过调整模型参数a和b,使多变量函数最小化[8]。用最小二乘法估计参数,参数a和b分别由式(3)和(4)表示为

2 变截面刚构桥主梁相关几何参数
2.1 边跨比
在变截面刚构桥主梁几何参数中,边跨比表示边跨跨长B1或者B2与最大跨径B之比,其中B1≥B2,选取边跨比较大值,即B1/B。
跨径的选择,重要的是边跨跨长与最大跨径比例问题。若边跨比太大,边跨结构整体刚度就会偏小。过小的刚度会导致主梁应力和挠度不容易控制,直接影响到结构的适应性和安全性。另外,吕志涛等研究表明,边跨比与梁体开裂存在较明显的相关性[9]。因此,如何才能选择最佳的比例,是设计的关键。从变形和受力的角度出发,朱汉华等给出了边跨比范围在0.6~0.7,为满足施工的需要可以选取较小值[10]。施颖等提出边跨与中跨的长度比控制在0.55~0.6范围内为宜[11]。牛和恩与周军生等认为,从取消落地支架,方便施工的角度出发,边、主跨比值在0.54~0.56,边墩支座上仍然保留有足够的正压力而不出现负反力,同时也不因为边跨无支架合龙而增加预应力索[12-13]。从搜集的大量文献可以看出,边跨比的建议范围并不一致,有的更宽泛一些,而有的更狭窄一些[14-17]。另外,基于已建桥梁的资料统计成果,邵旭东等给出了边跨跨长与中跨跨长之间的关系表达式[18]。
2.2 厚跨比
厚跨比表示变截面刚构桥主梁最大跨径跨中截面顶板厚度ttm、腹板厚度twm、底板厚度tbm与最大跨径B之比,ttm/B、twm/B、tbm/B。近年来,箱梁壁做得越来越薄,特别是腹板,从而消弱了箱梁的抗裂和抗剪能力,使混凝土箱梁更容易产生裂缝,从而影响桥梁的使用寿命。箱梁腹板主要承受竖向和扭矩产生的剪应力,根据剪应力要求选择腹板的最小厚度。同时,也要满足混凝土浇注施工质量的构造要求,来确定跨中腹板最小厚度。对于布置纵向和竖向管道的大跨径混凝土变截面刚构桥跨中腹板厚度来说,最小值不宜小于35 cm。宋建嫱给出跨中腹板厚度最小值不宜小于45 cm[15],高吉才等给出更小值为30 cm[16]。对于腹板厚度的确定,英国水泥和混凝土协会给出了两个最佳腹板厚度参数的公式以及国内学者提出的腹板厚度经验公式[18]。
跨中顶板厚度首先满足桥面板的受力要求,还要满足受力筋的构造要求,然后再根据腹板间距确定。施颖给出了构造要求的最小厚度为20 cm[11]。大多数文献给出最小厚度大于或等于25 cm以及相应的经验公式[10,14-15,19-20]。跨中底板厚度需满足正弯矩下力筋通过的构造要求,按无波纹管接长段为18 cm,有波纹管接长段为20 cm。通常情况下,底板厚度按照箱梁高度的1/10~1/12设计,一般为25~35 cm。
2.3 高跨比
高跨比表示变截面刚构桥主梁墩顶梁高hp、跨中梁高hm与最大跨径B之比,hp/B、hm/B。变截面箱梁高度选取直接关系到整桥工程量、外形美观以及施工难易程度等。适当增加梁高,可提高主梁刚度,增加抗剪承载能力,改善主梁应力状态,减少跨中挠度。但是,高跨比的增加,势必会增加主梁的自重。
关于梁高与最大跨径比值,主要从整桥结构受力方面做了大量的研究,并给出了相应的参考范围[11,14,16-19,21-22]。墩顶梁高与最大跨径比值一般在1/15~1/20之间,跨中梁高与最大跨径比值一般在1/30~1/50之间。在大跨径预应力混凝土连续刚构桥设计中,各国规范对高跨比均无明确规定[20]。因此,对该参数进行研究是很有必要的。
2.4 顶底板宽比
顶底板宽比表示变截面刚构桥主梁顶板宽度wts与底板宽度wbs之比,wts/wbs。近年来变截面刚构桥发展迅速,表现在跨度的增大和横截面构造的先进性,即大量结构采用单箱单室大挑臂的薄壁结构。这样以来,提高了变截面刚构桥的顶底板宽比。桥梁设计时,控制翼缘板悬臂长度在合理范围以内,否则需考虑多箱式截面形式;随着薄壁箱梁悬臂的增长,“剪力滞后”现象越严重[23],由于剪力滞效应,刚构桥中支点箱梁两侧翼缘常开裂渗水,也加快了使用过程中桥梁的侵蚀风化,降低了桥梁耐久性。因此,通过在役变截面刚构桥顶底板宽比的统计分析,找出参数的取值范围是必要的。
2.5 腹板厚度参数
英国水泥和混凝土协会提出2个关于预应力混凝土连续梁墩顶和跨中最佳腹板厚度参数的公式,其指标分别由式(5)和(6)表示为
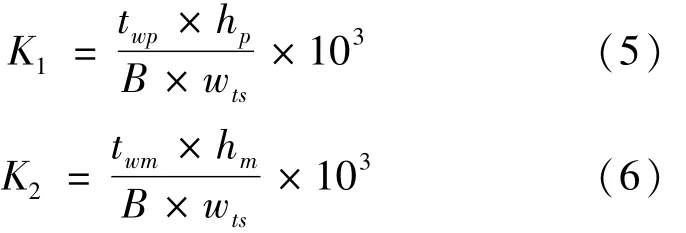
式中:K1、K2分别表示墩顶、跨中最佳腹板厚度参数;twp、twm分别为墩上和跨中腹板厚度总和,m;wts为桥面总宽度,m。
3 变截面刚构桥主梁的几何参数统计分析
3.1 边跨比统计分析
(1)边跨比与建成时间回归分析
收集了B≥120 m的三跨变截面刚构桥147座,选取国内跨径B≥120m的110座公路桥梁,分别对1989~2005年和2006~2015年2个时间段的边跨比与建成时间进行回归分析,建立回归线方程。1989~2005年和2006~2015年2个时间段的边跨比与建成时间回归分析曲线,如图1所示。1989~2005年边跨比与建成时间回归线方程由式(7)表示为

2006~2015年边跨比与建成时间回归线方程由式(8)表示为式中:B为最大跨径,m;B1为边跨跨径,m;y为建成时间,a。


图1 主梁边跨比与建成时间y回归分析图
从图1可以看出,1989~2005和2006~2015年期间桥梁边跨比随建成时间增加均有所减小,后者较前者更加趋向某一狭窄范围。前者回归线边跨比范围为0.566~0.626之间,平均值为0.5835,后者回归线边跨比范围为0.532~0.553之间,平均值为0.5437。
(2)边跨比与最大跨径回归分析
选取国内跨径B≥120 m的110座公路桥梁,分别对1994~2005年和2006~2015年2个时间段的边跨比与最大跨径进行回归分析,边跨比与最大跨径回归曲线如图2所示。

图2 主梁边跨比与最大跨径B回归分析图
1994~2005年边跨比与最大跨径回归线方程由式(9)表示为
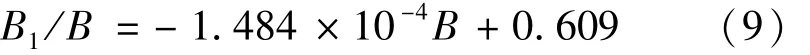
2006~2015年边跨比与最大跨径回归线方程由式(10)表示为

从图2可以看出,1994~2005年期间在役桥梁边跨比随跨径的增大而逐渐缩小,2006~2015年期间在役桥梁边跨比变化很小,其值主要集中在0.52~0.58之间。前者回归线边跨比范围为0.562~0.606之间,后者回归线边跨比范围为0.537~0.545之间。这说明2006~2015年期间在役桥梁边跨比与跨径之间无明显的相关性,边跨比设计更加趋向于0.54~0.55之间这一特定范围值。这种明显的变化趋势,与朱汉华等、施颖等所提供的范围一致[10-11],说明后者所设计的边跨比受力更合理、更能满足施工技术要求、更能创造经济效益。
3.2 厚跨比统计分析
收集了国内在役B≥120 m的三跨变截面刚构桥60座,分别对1989~2005年和2006~2015年2个时间段的厚跨比与最大跨径进行线性回归分析。1989~2005年和2006~2015年的刚构桥跨中截面厚跨比顶板、底板和腹板厚跨比与最大跨径回归分析曲线分别如图3和4所示。

图3 1989~2005年ttm/B、twm/B、tbm/B与B回归分析图

图4 2006~2015年ttm/B、twm/B、tbm/B与B回归分析图
1989~2005年期间twm/B、tbm/B、ttm/B与最大跨径回归线方程由式(11)、(12)和(13)表示为
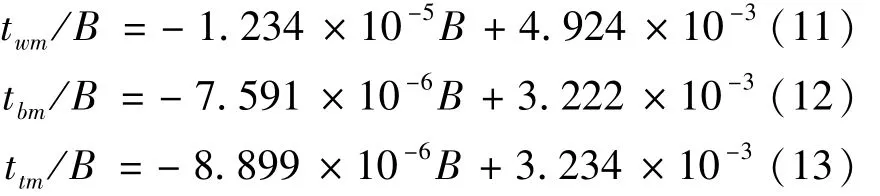
式中:ttm、twm、tbm分别为跨中截面顶板厚度、腹板厚度及底板厚度,mm。
由图3可以看出,刚构桥跨中截面顶板、底板、腹板厚跨比ttm/B、tbm/B、twm/B均随最大跨径B的增大而减小,twm/B数值离散性较大,设计时选取腹板厚度相差较大,如1989~2005年期间同一跨径桥梁跨中腹板厚度差达到25 cm。
2006~2015年期间twm/B、tbm/B、ttm/B与最大跨径的回归线方程由式(14)、(15)和(16)表示为
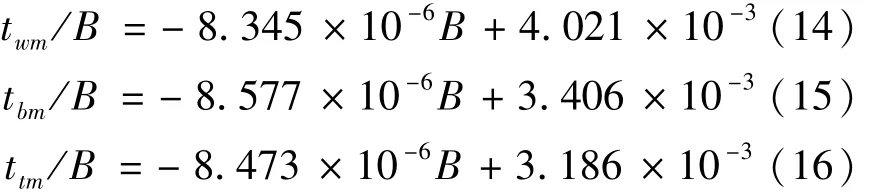
由图4看出,刚构桥跨中截面顶板、底板、腹板厚跨比ttm/B、tbm/B、twm/B数值分布相比较为集中,分别在40~55、25~32和30~40 cm之间,同一跨径twm/B差相对较小,最大差为10 cm。twm/B、ttm/B、tbm/B与最大跨径B回归线近似平行,说明跨径相同时跨中箱梁ttm/B、twm/B、tbm/B三者呈比例关系。
从图3和4对比可以看出,ttm/B、tbm/B变化并不明显,但在1989~2005年期间twm/B随B的增加数值减小较快。从跨径超过200 m的桥梁统计数据来看,2006~2015年期间twm更加趋向于40~50 cm之间,平均值较1989~2005年期间有所变小。
另外,根据ttm/B、tbm/B、twm/B与最大跨径B回归线近似平行关系,由式(14)、(15)和(16)得到跨中截面壁厚之间的关系表达式,由式(17)表示为
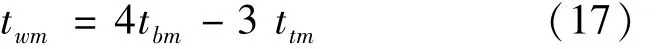
这说明国内2006~2015年期间已建跨径B≥120 m的三跨变截面刚构桥跨中截面壁厚的取值存在内在规律,为跨中标准横截面设计提供参考依据。
3.3 高跨比统计分析
3.3.1 不同时间段高跨比统计分析
收集跨径120 m及以上的三跨变截面连续刚构桥147座。其中,1989~2005年期间统计了71座,墩顶高跨比平均值为0.0554,跨中高跨比平均值为0.0192,墩顶梁高约为跨中梁高的2.89倍;2006~2015年期间统计76座,墩顶高跨比平均值为0.0594,跨中高跨比平均值为0.0208,墩顶梁高约为跨中梁高的2.86倍。分别对1989~2005年和2006~2015年2个时间段的高跨比与最大跨径进行线性回归分析,2个时间段的刚构桥墩顶、跨中高跨比与最大跨径回归分析曲线如图5所示。

图5 主梁高跨比与最大跨径B回归分析图
1989~2005和2006~2015年,hp/B、hm/B与B回归线方程由式(18)、(19)、(20)和(21)表示为

式中:hp、hm分别为墩顶、跨中箱梁高度,m。
根据图5分析可知,1989~2005年期间,hp/B、hm/B大致在0.05~0.06和0.015~0.022之间,hp/B随着跨径B的增大而增大,hm/B随着跨径B增大而减小;2006~2015年期间,hp/B、hm/B大致分布在0.055~0.065和0.017~0.024之间,hp/B随着跨径B增大变化很小,hm/B随着跨径B增大而减小,和1989~2005年期间变化相差不大。
回归分析表明,2006~2015年国内公路120 m及以上预应力混凝土连续刚构箱梁桥hp/B和hm/B值均有提高。适当增加梁高,可提高主梁刚度和抗剪承载能力,同时增加了自重,致使悬臂施工时恒载内力较大,上缘拉应力随之增加。因此,选取箱梁高跨比时,综合考虑两者影响,寻求最合理高跨比值。
根据式(14)、(16)、(20)和(21),推导出跨径B≥120 m的变截面刚构桥梁高比hp/hm与箱梁截面壁厚之间的关系表达式,由式(22)表示为

对于跨径B≥120m的三跨变截面刚构桥梁高的选取,可以由跨中箱梁壁厚的选取来拟定梁高,这梁高的选取和验证提供依据。
3.3.2 国内外高跨比统计分析
收集了国内外跨径在100 m及以上的三跨变截面连续刚构桥182座。其中,国内桥梁130座,国外52座。分别对1989~2005年和2006~2015年2个时间段的国内外跨径B≥100 m的三跨变截面刚构桥高跨比与最大跨径进行线性回归分析。刚构桥墩顶、跨中高跨比与最大跨径回归分析曲线如图6所示。

图6 国内外主梁高跨比与最大跨径B回归分析图
国内hp/B、hm/B与B回归线方程分别由式(23)和(24)表示为

国外hp/B、hm/B与B回归线方程分别由式(25)和(26)表示为

根据图6分析可知,国内变截面刚构桥主梁hp/B随着B的增大略有增大,然而国外hp/B随着B的增大而减小;国内外变截面刚构桥主梁hm/B均随跨径B增大而减小。国内变截面刚构桥主梁hp/B、hm/B围绕回归线分布比较集中,国外两者数值离散较大。特别强调的是,国外有6座桥梁跨中梁段采用了轻质混凝土,hp/B、hm/B可以做到1/20.6和1/86。由于减轻了自重,不需要承受更大的恒载弯矩,因此不需要采用更大的梁高来补偿。
3.4 顶底板宽比统计分析
统计分析了73座跨径B≥120m的三跨变截面刚构桥主梁顶底板宽比与最大跨径之间关系。分别对1994~2005年和2006~2015年2个时间段的国内跨径B≥120 m的顶底板宽比wts/wbs与最大跨径B进行线性回归分析,如图7所示。
根据图7,1994~2005年和2006~2015年2个时间段在役桥梁顶底板宽比离散性都较大,两者回归线随跨径变化趋势均不明显,说明wts/wbs与最大跨径无明显相关性。1994~2005年期间所统计桥梁wts/wbs平均值为1.94,比2006~2015年期间的1.83要大。2006~2015年期间在役桥梁在选取wts/wbs值时有所减小,说明在设计时更加注重翼缘有效宽度对剪力滞效应以及引起桥梁病害的影响。
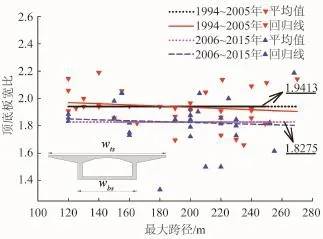
图7 顶底板宽比与最大跨径B回归分析图
3.5 腹板厚度参数统计分析
收集1988~2015期间国内已建跨径100m≤B≤200 m的三跨变截面刚构单箱室箱梁桥77座,并分别对1988~2005年和2006~2015年2个时间段的墩顶和跨中腹板厚度参数进行了统计分析,这2个时间段的刚构桥墩顶腹板厚度参数与墩顶最佳腹板厚度参数K1对比曲线、跨中腹板厚度参数与跨中最佳腹板厚度参数K2对比曲线分别如图8和9所示。
由图8和9可以看出,2006~2015年期间在役桥梁墩顶和跨中腹板厚度参数较最佳腹板厚度参数K1、K2均有所提高,且跨中提高幅度较大;1988~2005年期间,墩顶腹板厚度参数与最佳腹板厚度参数K1较为吻合,跨中有所提高。

图8 主梁墩顶腹板厚度参数与最佳腹板厚度参数K1对比图
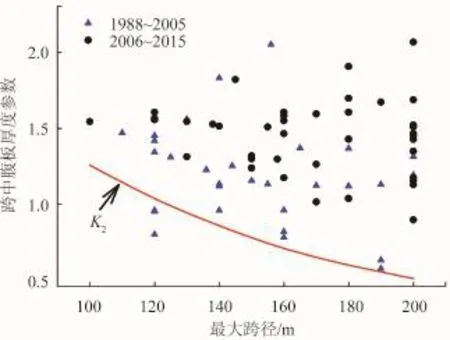
图9 主梁跨中腹板厚度参数与最佳腹板厚度参数K2对比图
4 结论
通过收集1988~2015年期间国内外最大跨径B≥100m的在役三跨变截面刚构桥主梁几何参数,按1998~2005年、2006~2015年2个时间段线性回归分析了几何参数随最大跨径或建成时间的变化关系,并进行对比,得到以下主要结论:
(1)边跨比集中分布在0.53~0.55之间,与1989~2005年期间的0.56~0.63相比选取范围更加狭窄,更加趋向某一特定范围,2个时间段边跨比均随建成时间的增加而减小,且与最大跨径无明显的相关性。
(2)最大跨径B≥200 m跨中截面腹板厚度在40~50 cm之间,分布比较集中,但twm平均值较1989~2005年期间有所减小,腹板厚度变薄会降低箱梁的抗裂和抗剪能力,影响桥梁的使用寿命。
(3)由墩顶、跨中梁高比集中分布在1/15.4~1/18.1和1/42~1/58之间,相比1989~2005年期间数值均有所提高,国内hp/B随着最大跨径B的增大而逐渐增大,国外却相反。由于采用轻质混凝土,国外的hp/B可以做到1/20.6。
(4)顶底板宽比平均值为1.83,相比1994~2005年期间的1.94有所减小,减小了翼缘板悬臂长度,且2时间段的wts/wbs均与最大跨径无相关性。
(5)墩顶和跨中腹板厚度参数普遍高于最佳腹板厚度参数K1、K2,且所统计的跨中腹板厚度参数偏离K2较大,而1988~2005年期间墩顶腹板厚度参数与K1吻合较好。
另外,国内已建三跨变截面刚构桥主梁跨中截面壁厚twm、ttm和tbm之间,与墩顶、跨中梁高比hp/hm之间存在明显的内在规律,建立几何参数之间的关系式,为跨中标准横截面设计提供参考依据。
[1] 黄志斌,罗旗帜,吴有俊.连续箱梁桥下挠分析及体外预应力加固评价[J].水利与建筑工程学报,2016,14(5):75-79.
[2] 刘超,徐栋.某预应力混凝土连续箱梁桥开裂和下挠病害处治[J].公路交通科技,2016(8):205-207.
[3] 林新元.预应力混凝土变截面连续箱梁裂后受力性能研究[D].西安:长安大学,2010.
[4] 马木欣.中小跨径桥梁边中跨比与连开裂关系的回归分析[J].交通科技,2010(2):24-27.
[5] 白莹莹.大跨度预应力混凝土连续刚构桥设计参数的研究[D].西安:长安大学,2011.
[6] Podolny W.,Muller J.M..Construction and Design of Prestressed Concrete Segmental Bridges[M].Melbourne:Krieger Publishing Company,1994.
[7] 陈久长.大跨连续刚构桥的参数分析及预应力优化[D].长沙:长沙理工大学,2014.
[8] VeltenK..Mathematicalmodeling and simulation[M].北京:国防工业出版社,2012.
[9] 吕志涛,潘钻峰.大跨径预应力混凝土箱梁桥设计中的几个问题[J].土木工程学报,2010,43(1):70-76.
[10]朱汉华,陈孟冲,袁迎捷.预应力混凝土连续箱梁桥裂缝分析与防治[M].北京:人民交通出版社,2009.
[11]施颖,郑建群.从结构层面探讨预应力混凝土连续箱梁桥裂缝控制[J].重庆交通学院学报,2005,24(4):13-18.
[12]牛和恩.虎门大桥工程(第三册):主跨270 m连续刚构桥[M].北京:人民交通出版社,1999.
[13]周军生,楼庄鸿.大跨径预应力混凝土连续刚构桥的现状和发展趋势[J].中国公路学报,2000,13(1):31-37.
[14]王仁贵,吴伟胜,庞颂贤.预应力混凝土连续刚构桥设计[C].成都:2003年全国桥梁学术会议,2003.
[15]宋建嫱.大跨径预应力混凝土变截面连续桥梁设计[J].中国水运,2012,12(11):200-201.
[16]高吉才,金庆利.大跨径PC变截面连续梁设计要点探讨[J].中外公路,2010,30(6):125-128.
[17]戴竞.预应力混凝土连续梁桥设计与施工[J].土木工程学报,1980(2):1-15.
[18]邵旭东,程翔云,李立峰.桥梁设计与计算(第2版)[M].北京:人民交通出版社,2012.
[19]楼庄鸿.楼庄鸿桥梁论文集[M].北京:人民交通出版社,2004.
[20]李强.预应力混凝土连续刚构桥的发展及存在的问题[J].交通标准化,2009(10):9-13.
[21]李晓克,刘世明,杨竹林.预应力混凝土连续箱梁桥设计实例分析[M].北京:中国电力出版社,2015.
[22]陈杰超,胡伟,宁晓骏,等.大跨连续刚构桥箱梁高度与主跨比值研究[J].重庆建筑,2008,56(6):24-27.
[23]张元海,林丽霞.薄壁箱梁剪力滞效应分析的初参数法[J].工程力学,2013,30(8):205-211.
Statistical analysis ofmain grider geometric parameters of variable cross-section rigid frame bridges
Xu Gangnian,Wang Youzhi*,An Ran,et al.
(School of Civil Engineering,Shandong University,Jinan 250061,China)
The study on the value and inherent laws of the geometric parameters can provide some reference for bridge designers.Based on the data collected from the domestic and international bridges,the least-squaresmethod was applied to regression analysis of the height-span ratio,sidemain span ratio,thickness-span ratio,width ratio of top and bottom slab,the web thickness parameters of the pier-top and mid-span section varying overmaximum span or bridge service time. The analytical results indicate that the side-main span ratio generally ranges from 0.53~0.55 during 2006~2015,which is a huge difference between 0.56~0.63 during 1989~2005,but does not obviously correlate with themaximum span.Theweb thickness of themid-spansection for bridgeswith B≥200 m is approximately distributed in 40~50 cm,and the average level is lower than the web thickness during 1989~2005.The height-span ratio of the beam on the pillars and in themiddle of span ranges from 1/15.4 to 1/18.1 and 1/42 to 1/58 respectively,which are higher than the levels in 1989~2005.The height-span ratio of the pier-top from the domestic increases with the maximum span,but the value from the foreign opposites.There is no convincing correlation between the width ratio of top to bottom slab and the maximum span.The average value of the width ratio of top and bottom slab is1.83 during 2006~2015,less than 1.94 during 1994~2005.The thickness parametersof theweb with the pillars and themiddle of span deviate from the optimal value during 2006~2015,and the latter deviates more.During 1988~2005,the thickness parameter of the pier-top web is agreementwith the optimal value K1.
variable cross-section rigid frame bridge;geometric parameters of main grider;leastsquaresmethod;regression analysis
U443.35
:A
1673-7644(2017)02-0137-07
2017-02-07
国家自然科学基金项目(11372165);交通运输部西部交通建设科技项目(2011318223940)
徐刚年(1982-),男,讲师,在读博士,主要从事结构工程维修加固、新型结构材料开发等方面的研究.E-mail:xugangnian2007@163.com
*:王有志(1964-),男,教授,博士,主要从事结构工程评估与维修加固、新型结构材料开发等方面的研究.E-mail:wangyouzhi@sdu.edu.cn
