双分数跳-扩散过程下后定选择权定价

薛红,王银利

(西安工程大学 理学院，西安 710048)

双分数跳-扩散过程下后定选择权定价

薛红,王银利

(西安工程大学 理学院，西安 710048)

假定股票价格服从双分数布朗运动和泊松过程共同驱动的随机微分方程,股票预期收益率,无风险利率和股价波动率均为常数,建立双分数跳-扩散环境下金融数学模型,利用保险精算方法,结合双分数跳-扩散随机分析理论研究后定选择权定价问题,得出了双分数跳-扩散环境下后定选择权定价公式。

后定选择权;双分数布朗运动;跳-扩散过程;保险精算方法

随着期权市场的发展,期权定价成为金融工程学研究的核心问题。后定选择权是一种允许持有人在特定时间点选择看涨或者看跌的新型期权。由于股票价格会因为一些突发状况而出现跳跃,近年来不少学者考虑用Poisson过程和布朗运动或分数布朗运动共同驱动的随机微分方程来描述股票价格变化,文献[1]假定股票价格服从分数布朗运动和非时齐Poisson过程共同驱动的随机微分方程,且无风险利率和波动率为时间的非随机函数的条件下,得出了欧式期权的定价公式。文献[2]在布朗运动环境下假定股票价格满足跳扩散过程驱动的随机微分方程,利用测度变换方法给出了欧式任选期权的定价公式。由于布朗运动的增量具有平稳性和独立性,使得它只能描述未来股价与过去无关的股票价格变化过程,这使得对期权价格的研究具有很大的局限性。文献[3]假定股票价格服从分数跳-扩散过程驱动的随机微分方程,利用分数跳-扩散理论及保险精算方法,得出了分数跳-扩散过程下后定选择权的定价公式。双分数布朗运动是一种比分数布朗运动更一般的高斯过程,其既不具有平稳增量,也不具有独立增量,使得它可用来描述股票价格变化。文献[4-5]阐述了双分数布朗运动的概念和性质。文献[6]假定股票价格服从双分数布朗运动和跳过程驱动的随机微分方程,运用保险精算方法得出了双分数跳-扩散过程下欧式期权定价公式。文献[7]首次提出保险精算方法,与鞅方法或测度变换方法相比,保险精算方法将期权定价问题转化为等价的公平保费问题,不存在任何经济假设,在计算数学期望时使用的是股票价格过程的实际概率测度,这样使得它不仅对均衡,无套利,完备的市场有效,并且对非均衡,有套利,不完备的市场也有效。关于保险精算方法在期权定价中的应用见文献[8-10]。本文假定股票价格服从双分数布朗运动和Poisson过程共同驱动的随机微分方程,运用双分数跳-扩散随机分析理论,利用保险精算方法得出了后定选择权的定价公式。

1 金融数学模型

假定股票价格St满足随机微分方程

(1)

引理1.1 随机微分方程(1)的解为

(2)

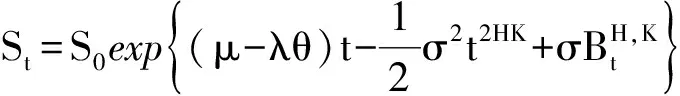
假定只在t1∈[0,t]时刻发生了一次跳跃,则在[0,t1)时间段内有

同理在(t1,t]时间段内有

由(1)式有

从而有

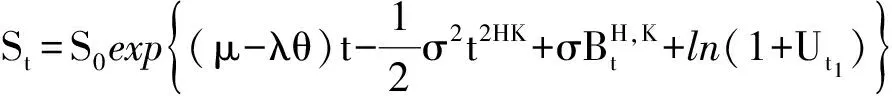
所以,当跳跃次数服从Poisson过程时可得结果。

定义1.2[7]股票价格过程{St,t≥0}在[t,T]上的期望回报率βu,u∈[t,T]定义为

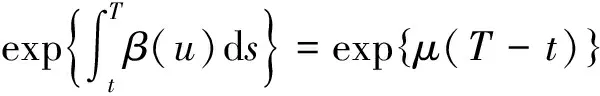
证明 由(2)式有

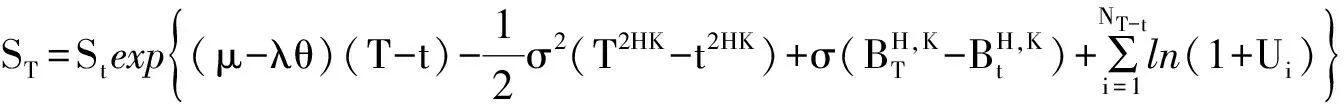
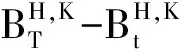
又因为{Ui,i≥1}为独立同分布列,有

所以有E[ST]=Stexp{μ(T-t)}, 从而可得结果。

2 后定选择权权定价

定义2.1[7]欧式看涨期权在t时刻的保险精算价格定义为

(3)

其中r表示无风险利率,

欧式看跌期权在t时刻的保险精算价格定义为

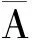
定理2.2 欧式看涨期权在t时刻的保险精算价格

欧式看跌期权在t时刻的保险精算价格

其中N(x)为标准正态分布函数,且

证明 先来证明欧式看涨期权的定价公式。 由定义2.1有

令

则A={ξ>-d}.由(3)式及保险精算定义可知

其中

且X～N(0,1),同时

同理可得欧式看跌期权的定价公式。

推论2.3 当K=1时,可得文献[1]的结果。

推论2.4 欧式看涨、看跌期权的平价关系式为

其中C(St*,t*)和P(St*,t*)分别表示欧式看涨、看跌期权在t*时刻的保险精算价格。

由欧式看涨、看跌期权平价关系可知,后定选择权在t*时刻的现金流为

(4)

定理2.6 在t*时刻选择看涨或看跌期权的后定选择权在选择时点前任意时刻t(0

其中N(x)为标准正态分布函数,且

证明 令

其中

且Y～N(0,1),同时

从而定理得证。

推论2.7 当K=1时,可得到分数跳-扩散过程下的后定选择权定价(见文献[3])。

推论2.8 当λ=0时,可得双分数布朗运动环境下后定选择权定价公式。

[1] 隋梅真,张元庆.分数布朗运动和泊松过程共同驱动下的欧式期权定价[J].山东建筑大学学报,2008,23(1):70-73.

[2] 黄国安,邓国和,霍海峰.跳-扩散过程下欧式任选期权的定价[J].山西大学学报(自然科学版),2008,31(3):438-442.

[3]XueH,HuangK.ChooserOptionPricingModelunderFractionalJump-diffusionOrnstein-UhlenbeckProcess[C]∥Proceedingsof2011InternationalConferenceonManagementScienceandEngineering,Chengdu,China,2011:533-538.

[4]RussoF,TudorC.Onthebi-fractionalBrownianMotion[J].Stochastic Processes and Applications,2006,116(5):830-856.DOI:10.1016/j.spa.2005.11.013.

[5] 肖玮磷,张卫国,徐维东.双分式布朗运动下股本权证的定价[J].系统工程学报,2013,28(3):348-354.

[6]XueH,WuJ.PricingEuropeanOptionunderBi-fractionalJump-DiffusionProcess[C]∥Proceedingsof2015InternationalConferenceonAdvancedICTforEducation,Guangzhou,China,2015:267-270.

[7]BladtM,RydbergTH.AnActuarialApproachtoOptionPricingUnderthePhysicalandWithoutMarketAssumptions[J].Mathematics and Economies,1998,22(3):65-73.DOI:10.1016/S0167-6687(98)00013-4.

[8] 闫海峰,刘三阳.广义Black-Scholes模型定价新方法——保险精算方法[J].应用数学和力学,2003,24(7):730-739.

[9] 郑红,郭亚军.保险精算方法在期权定价模型中的应用[J].东北大学学报(自然科学版),2008,29(3):429-432.

[10] 邓英东,范允征.相依于时间的交换期权的保险精算定价[J].合肥工业大学学报(自然科学版),2007,30(8):1069-1072.

Pricing Chooser Option Under Bi-fractional Jump-diffusion Process

XUE Hong,WANG Yinli

(SchoolofScience,Xi’anPolytechnicUniversity,Xi’an710048，China)

Assume that the stock price satisfy the stochastic differential equation driven by Bi-fractional Brownian and jump process, the expected return rate, interest rate and volatility rate are constant, the financial mathematics model is built, and the pricing problem of the chooser option is discussed by the theory of bi-fractional Brownian and jump process. The pricing formula of the chooser option is obtained by the actuarial approach.

chooser option;bi-fractional Brownian motion;jump-diffusion process;actuarial approach

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.01.009

2016-03-30；

2016-10-20

陕西省自然科学基金(2016JM1031)；陕西省教育厅专项科研基金(14JK1299)

薛红(1964-),男,山西万荣人,博士,教授,从事随机分析与金融数学研究,E-mail:xuehonghong@sohu.com

F830;O211

A

0253-2395(2017)01-0051-06