一种适用于不同分类器的样本约简算法

程汝峰，梁永全，刘 彤

(山东科技大学 计算机科学与工程学院，山东 青岛 266590)

一种适用于不同分类器的样本约简算法

程汝峰，梁永全，刘 彤

(山东科技大学 计算机科学与工程学院，山东 青岛 266590)

现有的样本约简算法多数是针对某种分类器设计的，在实际应用中有一定的局限性。结合聚类算法的思想，设计了一种适用于不同分类器的样本约简算法，核心是选取密度高且距离相对较远的样本点。与其他样本约简算法相比较，该算法可以根据需求获得任意大小的样本子集，并适用于多种分类算法；而对包含噪声点的样本集，算法的分类精度和稳定性均有一定程度的提高。

样本约简；准则；密度；样本子集

一般来说，不同样本的重要程度是不同的。一些冗余和噪音数据不仅造成大量的存储耗费，而且还会影响学习精度。因此更倾向于根据一定的性能标准，选择代表性样本形成原样本空间的一个子集，之后在这个子集上进行学习。在保持某些性能的基础上，最大限度地降低时间、空间的耗费。

样本约简算法根据性能的要求大致可分为增强型、保持型和混合类型三类。增强型算法的代表有ENN(edited nearest neighbor)[1]、RENN(repeated ENN)[2]、AKNN(aggregate k nearest neighbor)[3]等；保持型算法的代表有CNN(condensed nearest neighbor)[4]、RNN(reduced nearest neighbor)[5]、MCS(minimal consistent set)[6]、FCNN(fast nearest neighbor condensation)[7]等；混合型算法的代表性工作有ICF(iterative case filtering algorithm)[8]、DROP3(decremental reduction optimization procedure)[9]等。文献[10]和文献[11]对样本约简算法进行了很好的综述。

近几年，研究者尝试用不同的方法来实现样本约简。针对支持向量机，Chen等[12]提出一种可以加速支持向量机训练的样本约简算法；针对贝叶斯分类器，Pabitra等[13]提出一种多尺度的样本约简算法；基于保留区分数据超平面和最大化间隔的思想，文献[14]提出了一种间隔最大化的样本约简算法；基于超矩形聚类算法的思想，文献[15]提出了一种能够有效剔除非边界数据、保留边界和邻近边界数据的样本约简算法；基于谱图理论，文献[16]提出了一种能够有效划分数据集边界和内部实例的谱图样本约简算法；基于K-MEANS聚类算法的思想，文献[17]提出了一种能够处理较大数据集的高效样本约简算法；基于部分剔除的思想，文献[18]提出了一种仅剔除可疑噪声数据部分属性的部分样本约简算法。

通过分析可以发现，现有的样本约简算法或者是针对某种分类器设计，或者是倾向于选择边界数据。由于边界数据通常较稀疏并且很可能存在噪声，对原始样本集的代表性较差，很难适用于不同的分类算法。受文献[19]的启发，结合已有的约简准则，本文提出了一种新的样本点选取标准，该标准不针对于某种特定分类器，核心思想是选取密度高且相互之间距离相对较远的样本点。实验表明该标准在多种分类器上都有好的表现，有效地提高了样本约简效果。

1 理论基础

1.1 已有的约简准则

已有的约简准则多数为不确定性准则，通常是选择不确定性信息量大的样本。不确定性的度量方法有多种，相对应的准则也有多个。

最小置信度准则[20]是用概率学习模型计算或估计样本的后验概率。最大熵准则[21]是用信息熵度量样例的不确定性。投票熵准则[22]是综合若干个概率学习模型度量不确定性。一致性约简准则的核心概念是最近异类近邻子集[6]，最小一致子集样本约简算法(MCS)就是用这种度量标准来选择样例，生成最小一致子集。

1.2 精英点约简准则

已有的约简准则忽视了样本的分布信息。本文基于密度和距离的方法提出新的样本点选取准则。在这里称原始样本集中的数据为原数据，被选择出来的样本子集中的数据为精英点。以支持向量机(support vector machine,SVM)[23]为例，如果选择了具有代表性的数据，则对应的分类超平面应该非常接近“正中间”，并且能够有效排除噪声点的影响。从图1可以看出，通过精英点训练得出的分类器更具有通用性。

图2[14]表示的是一组按密度排序的样本分布图，图中数字是按密度降序后各个样本的编号。从图2中可以看出，如果仅考虑密度因素，样本点1～9都比样本点10的密度大，故选取的前9个精英点为样本点1～9。显然这样的选取过于集中，对整个样本集的代表性较差，如果存在重复的数据则效果更差。为了使选择的精英点更具有代表性，则需要更加分散，因此需要考虑距离因素。根据以上分析，易知精英点应同时具有两个特点：精英点本身的密度要高；精英点与其他密度较大的数据点之间的距离要大。

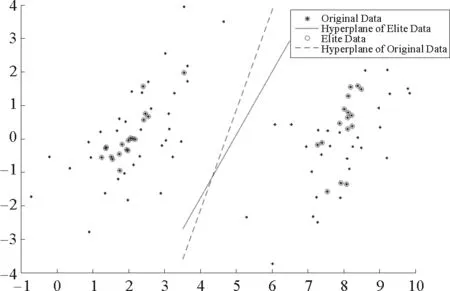
图1 精英点和相对应的分超平面Fig.1 Elite data points and corresponding classified hyperplane

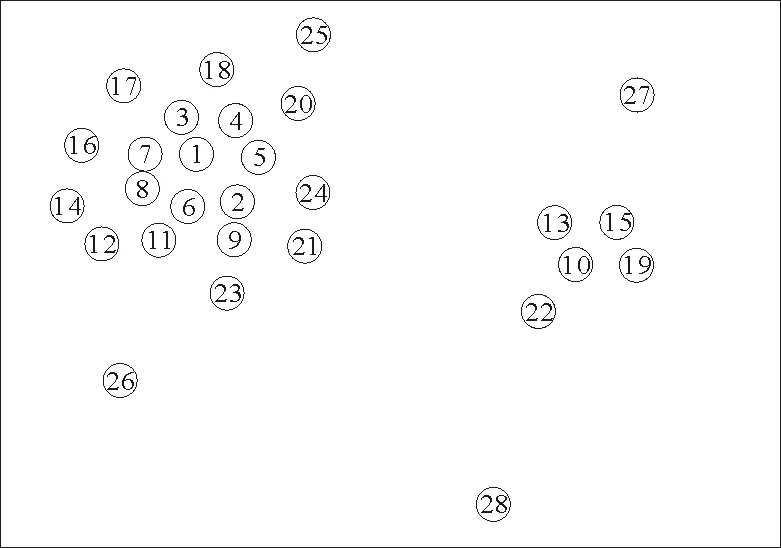
图2 一组按密度排序的样本分布图Fig.2 A set of instance distribution according to the density sort

1.2.1 密度的计算

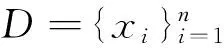
局部密度ρi包括截断核和高斯核两种计算方式：

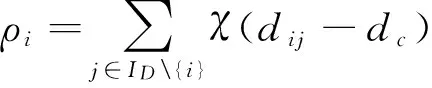
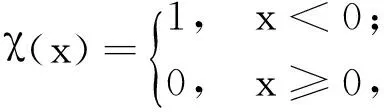
截断核为离散型而高斯核为连续型，因此相对来说后者产生冲突的概率更小。此外对于高斯核，如果与xi的距离小于dc的数据点越多，则ρi的值越大。

1.2.2 高密度点距离

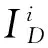
(1)

式(1)含义为：当xi具有最大局部密度时，δi表示与xi的距离最大的数据点与xi之间的距离；否则，δi表示在所有局部密度大于xi的数据点中与xi距离最小的数据点与xi之间的距离。

1.2.3 精英点综合考察量

综合两种因素，定义一个将局部密度ρi和高密度点距离δi综合考虑的量

γi=ρiδi,i∈ID。

(2)

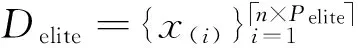
(3)

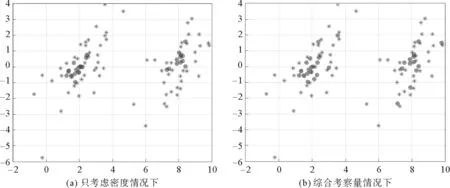
图3 精英点选取情况对比Fig..3 Comparison of elite selection

根据给出的γ值标准，可以对样本数据进行选取。图3是保留比例为30%情况下，精英点选取情况对比其中被圈出的点是精英点。

2 样本约简算法

基于精英点选取标准，提出了基于密度的DBES(density-basedeliteselecting)样本约简算法如下：

输入:样本集D,阈值截取位置Pdc,精英保留比例Pelite输出:样本子集Delite1.计算得到距离矩阵Dd;2.根据Pdc得到对应位置的dc及密度ρ;3.for样本集中的每一条数据xi4. Ifxi具有最大局部密度5. 找到与xi的距离最大的数据点xj;δi=dij;6. else7. 找到密度比xi大的数据点中,与xi距离最小的数据点xk;δi=dik;8. endif9.endfor10.计算γ值;根据Pelite值保留对应百分比的样本集Delite。

算法中，样本集D表示的是带约简的原始样本集；Pdc决定了算法所得到密度的有效性，同时也会影响到选取样本子集的有效性；Pelite决定了样本子集的大小，可以根据需要进行设定。关于Pdc和Pelite这两个参数的设定将在第3.3节进行讨论。

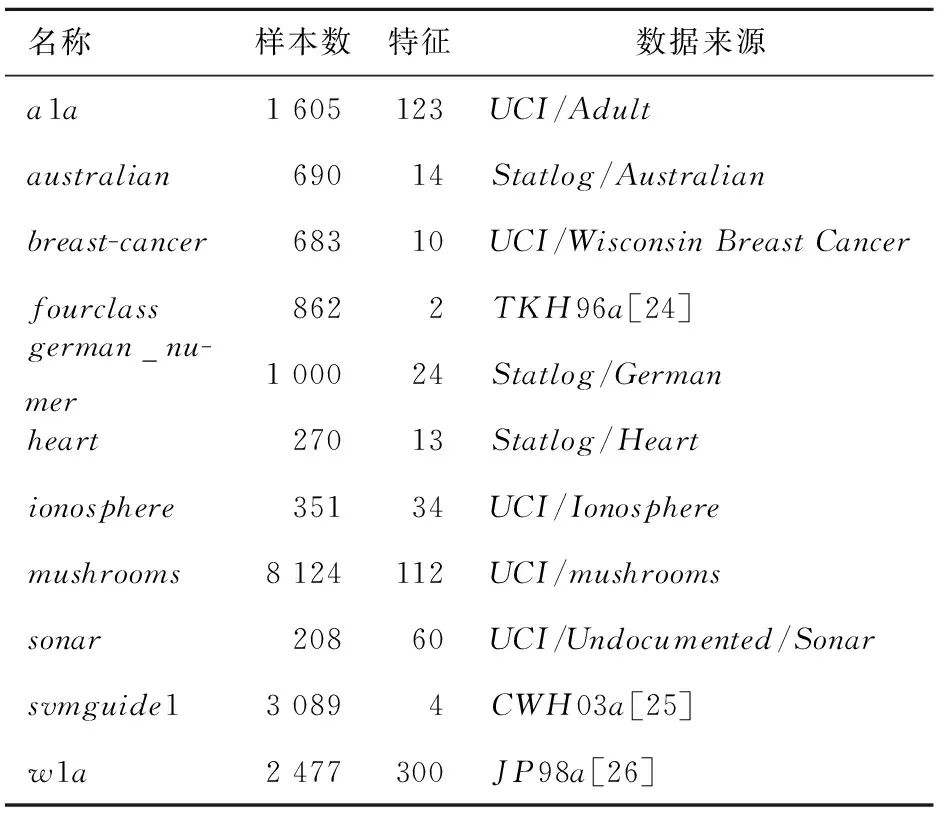
表1 样本集说明

假设样本集中包含数据点个数为n，计算距离矩阵Dd的时间复杂度为O(n2)。由于距离矩阵Dd是对称矩阵，所以在实际计算时可以计算一个上三角矩阵，节省一半的计算时间。计算δ值，需要比较两两之间的密度，时间复杂度为O(n2)。和计算距离矩阵Dd类似，根据矩阵的对称性可以节省一半的时间。算法中其他部分时间复杂度很低，因此整个算法的时间复杂度为O(n2)。

3 实验分析与讨论

实验包括三部分。3.1节是本文算法与其他样本约简算法的对比实验，对算法的约简比例和在分类算法上的分类精度进行了实验。其中用于对比的样本约简算法考虑到了所属类别以及影响力[11]，用于测试的分类算法包括SVM、KNN和C4.5三种不同类型的分类算法。3.2节是样本约简后对分类的影响实验。3.3节是算法约简稳定性及参数设置的分析实验，通过实验给出了DBES算法的参数设置建议。

实验所用样本集见表1，表2是选择对比的样本约简算法。

3.1 约简算法实验对比

本节选择了几种不同类型的算法进行对比分析。表3是样本约简比例(reductionrate,RR)的对比。表4～7是分类精度的对比，其中DBES1和DBES2分别表示：在Pdc取值分别为0.02的情况下，Pelite取值为0.3和取值为0.5时的计算结果。

表2 选择对比的样本约简算法

从表3可以看出，MCS算法在w1a样本集上没有实现有效约简，样本集大小无变化；在mushrooms样本集上，MCS、ICF和DROP3算法得到的样本子集偏小，而RENN算法得到的样本子集和原样本集相同，约简效果较差；相比于其他算法，DBES算法可以对样本集进行有效约简，并且根据Pelite的不同，可以得到任意大小的样本子集。通过调整参数Pelite，可以使得约简比例高于其他的几种算法。

表3 样本约简比例对比

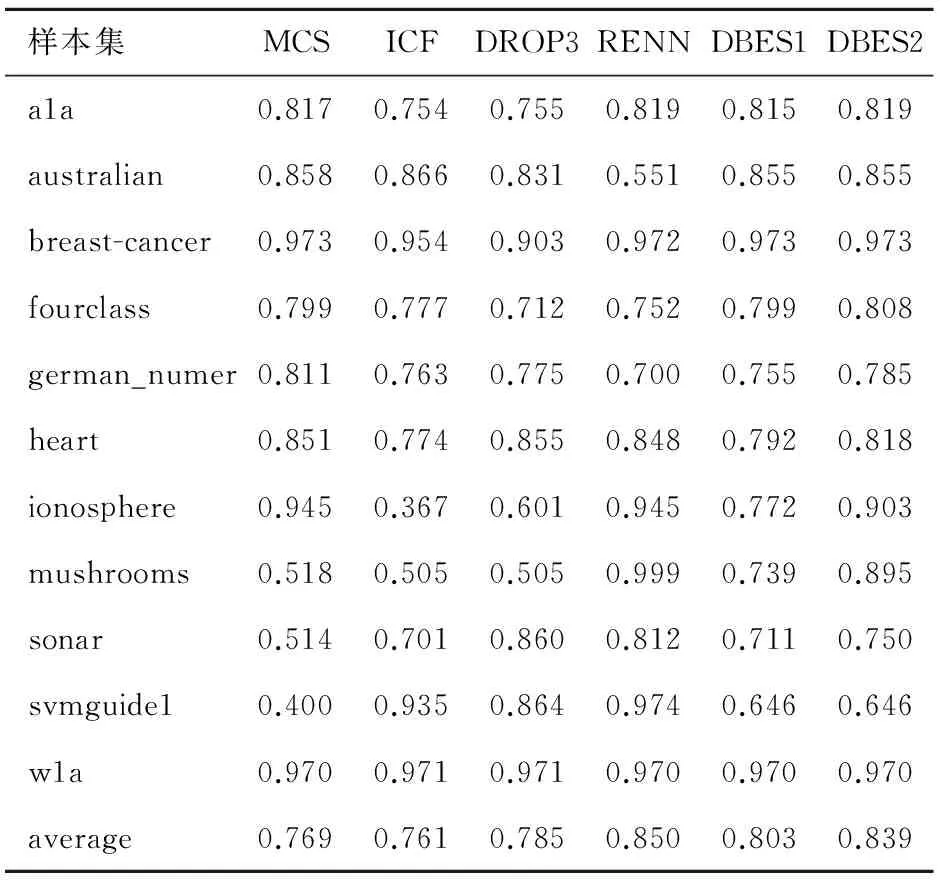
表4 样本子集分类精度对比(SVM)

表4是样本子集的分类精度对比，使用约简后的样本子集作为训练集，用LIBSVM进行训练得到分类模型，在测试集上进行测试得到分类精度。表格中average行表示样本约简比例以及样本子集分类精度的均值。表5和表6分别是KNN算法和C4.5算法的实验结果。结合表3、表4和表5可以看出，采用不同的分类算法测试，DBES算法都有较好的表现，其中在决策树(C4.5)算法下的优势最为明显。由于提出的准则以及算法不针对某种分类器，因此受分类算法的影响较小；与之相比较，其他算法受分类算法的影响较大。另外，对比3个表中DBES算法在Pelite不同取值时的分类精度可以看出，增大Pelite可以提高DBES算法的分类精度。

通过表3～6中的average可以看到，有的算法对样本集平均约简比例较大，但分类精度偏低，如DROP3算法；有的算法分类精度较高，但对样本集平均约简比例较小，如RENN算法；相比较于其他的方法，DBES算法能够在两个方面都保持较好的效果。

为了更好的说明DBES算法的优越性，采用文献[11]中的约简算法比较方法，将约简比例和分类精度的乘积作为新的综合指标，得到约简效果是综合指标对比如表7，从表中可以看出DBES算法(Pelite=0.3)的综合指标最高且非常稳定。

表8和图4是各个算法在不同样本集上分类精度和约简比例的方差。方差的大小反映了算法的稳定性。DBES算法可以根据参数将样本集约简到指定大小，约简稳定性高；对比不同分类算法上的分类精度方差可以发现，本文提出算法方差都非常小，分类精度的稳定性也明显好于其他算法。

3.2 约简算法对分类的影响

本节以SVM为例，采用交叉验证的方式，对算法进行了测试。实验选择了fourclass、heart和a1a样本集。其中fourclass是人工数据集，heart是低维真实数据集，a1a是高维真实数据集。实验结果如图5～7所示，图中实线代表约简后的分类精度及其均值，虚线代表原样本集分类精度及其均值。

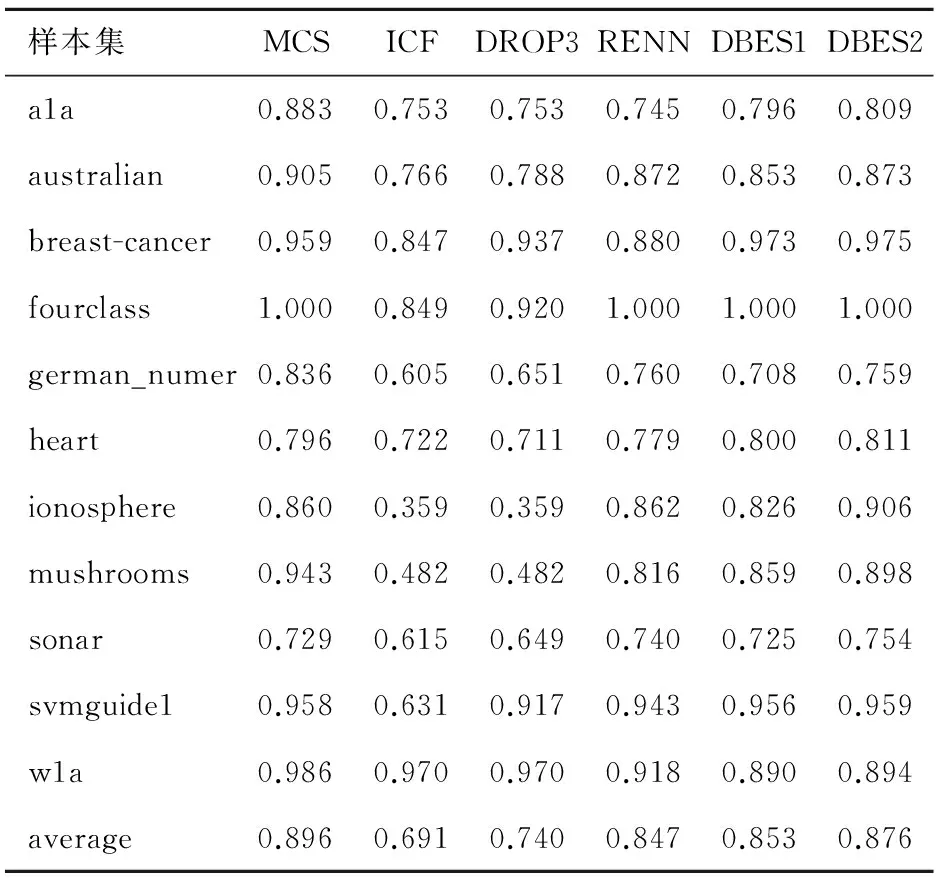
表5 样本子集分类精度对比(KNN)

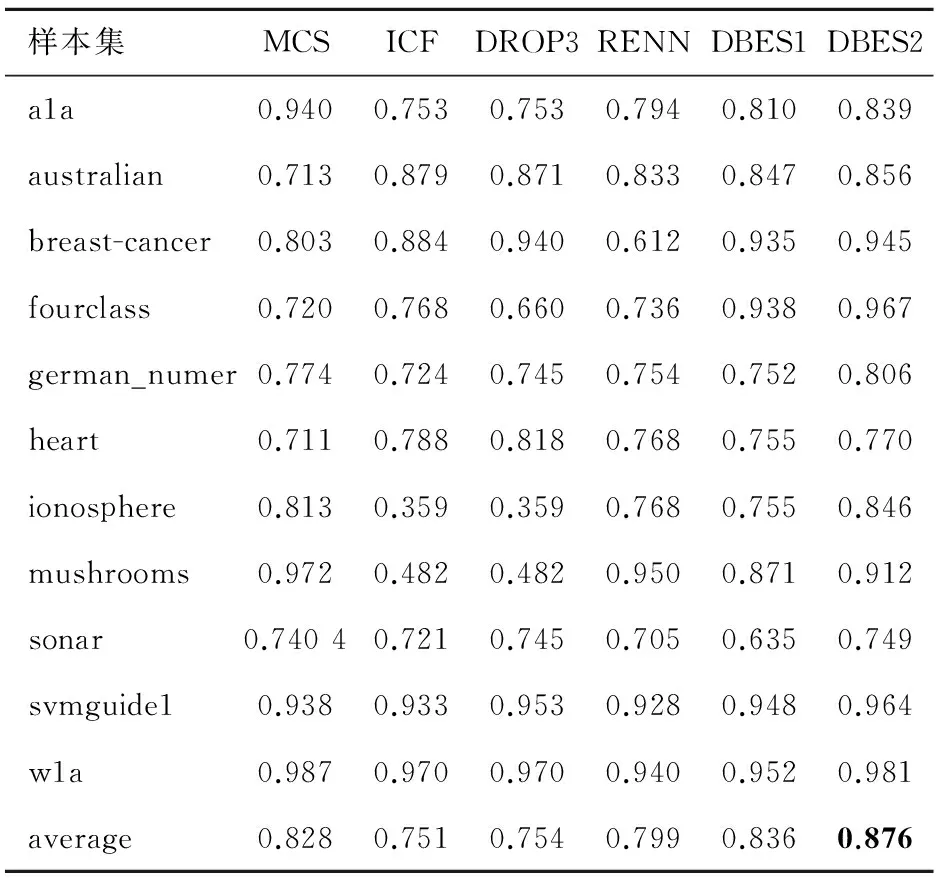
表6 样本子集分类精度对比(C4.5)

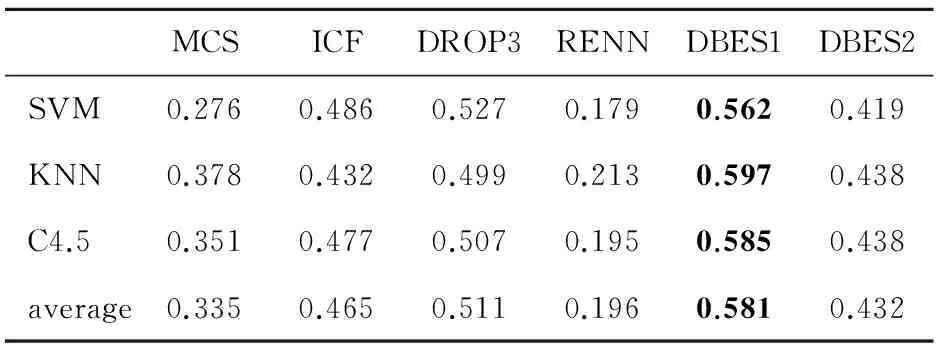
表7 约简效果综合指标对比

表8 约简比例和分类精度的方差

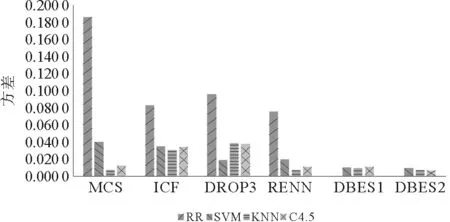
图4 约简比例和分类精度的方差Fig.4 Variance of reduction ratio and classification accuracy

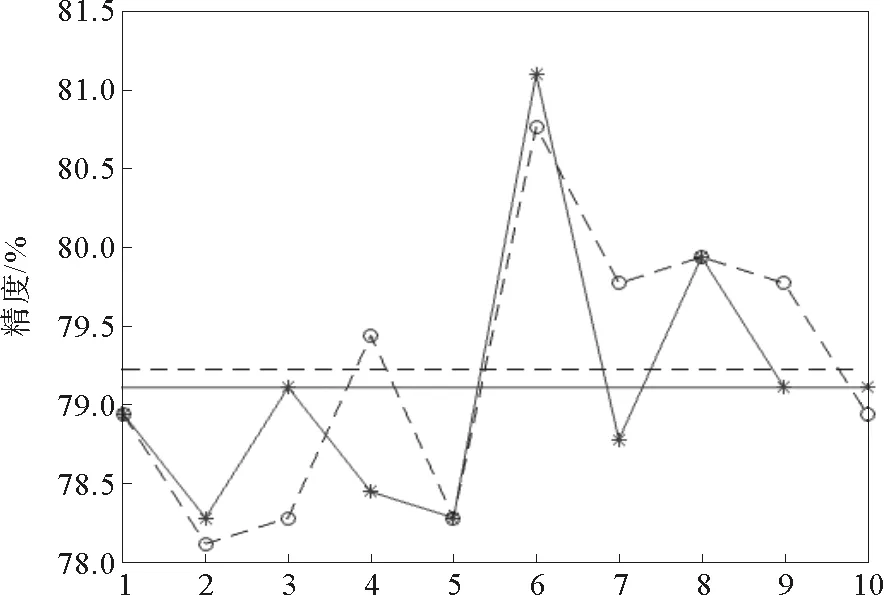
图5 fourclass随机抽样验证结果Fig.5 Random sample validation results of data set 1

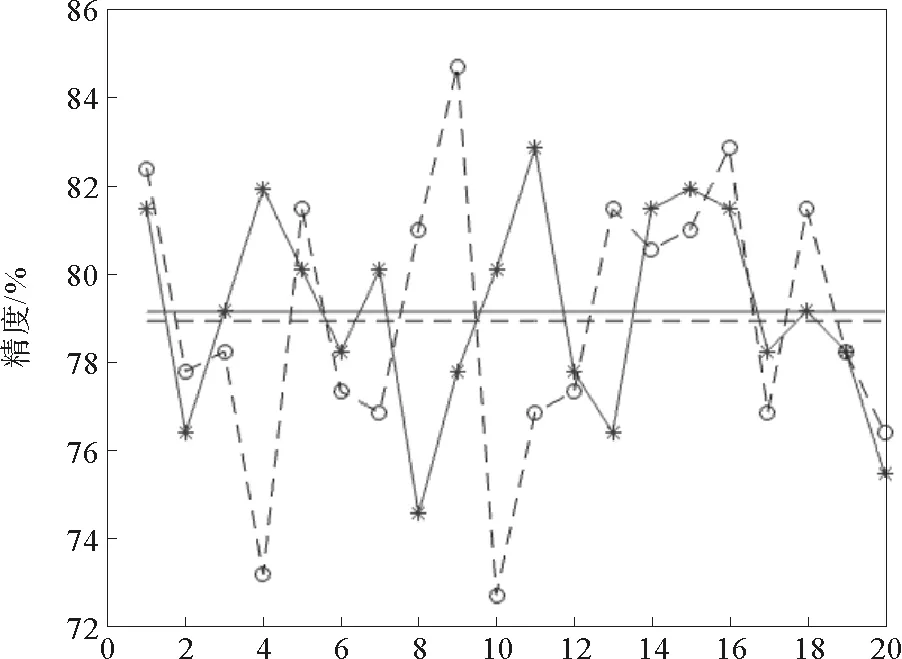
图6 heart随机抽样实验结果Fig.6 Random sample validation results of data set 2

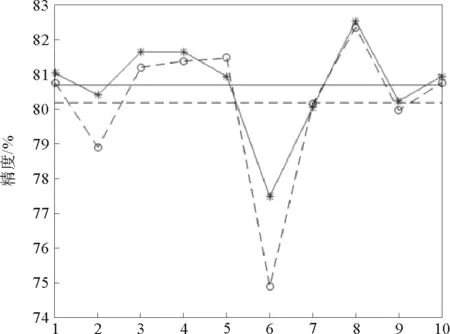
图7 a1a降维后的实验结果Fig.7 Results of data set 3 after dimension reduction

在fourclass上进行试验，随机抽样10次，抽取比例为50%，阈值截取位置Pdc=0.2，精英保留比例Pelite=0.25。由图5可以看出，因为fourclass为人工样本集合，样本点是使用算法按规则产生的，随机抽样验证结果的均值非常接近，其中有些情况下的精度甚至超过了原样本集的结果。

在heart上进行试验，随机抽样20次，抽取比例为50%，阈值截取位置Pdc=0.2，精英保留比例Pelite=0.3。由图6可以看出，该算法在该样本集上有较好的表现，约简后样本子集的分类结果甚至超过了原样本集的结果。真实数据中存在噪声数据，使用这样的数据进行训练，分类模型很可能受到噪声数据的影响。提出的约简算法能够过滤掉噪声数据，从而提高分类精度。

DBES算法在处理高维数据时效果有所下降。由于高维数据的稀疏性，将低维空间中的距离度量函数应用到高维空间时，随着维数的增加，数据对象之间距离的差异将不复存在，其有效性大大降低。实际应用中最常用的是PCA降维的方法。图7是对a1a使用PCA降到10维之后的实验结果，随机抽样10次，抽取比例为50%，阈值截取位置Pdc=0.02，精英保留比例Pelite=0.3。

通过以上实验可以看出，提出的样本约简算法能够较好地保持原分类算法的分类精度；对某些包含噪声的样本集合能够提高分类精度；对于高维数据经过降维处理之后，也能保持分类精度。

3.3 算法中参数的讨论

算法中包含三个参数，除了参数D，其他两个参数都需要给定。其中Pdc决定了算法所得到密度的有效性，Pelite决定了样本子集的大小。Pdc和Pelite的取值都在(0,1]之间并且由用户给定。图8表示的是Pelite=0.3时，Pdc取值变化对分类精度的影响(其中横轴代表Pdc取值变化，纵轴代表分类精度百分比)。图9表示的是Pdc=0.2时，Pelite取值变化对分类精度的影响(其中横轴代表Pelite取值变化，纵轴代表分类精度百分比)。

从图8中可以看出，Pdc的取值在[0.1,0.4]区间有较稳定的表现，取值过大或过小都会影响算法的稳定性；虽然在某些样本集上如ionosphere，随着Pdc的增大，分类精度有所提升，但在大部分样本集上，都会保持不变或者下降。从图9中可以看出，当Pelite的取值小于0.2时，分类精度会出现较大的波动。结合实际分析，保留更多的样本点意味着保留了更多的信息，会提高分类的精度。Pelite的增大意味着保留的样本子集逐渐增大，当Pelite值为1时意味着没有约简。所以，Pelite的取值可以根据样本数据和实际需求自行设定，建议取值区间为[0.2,1]。

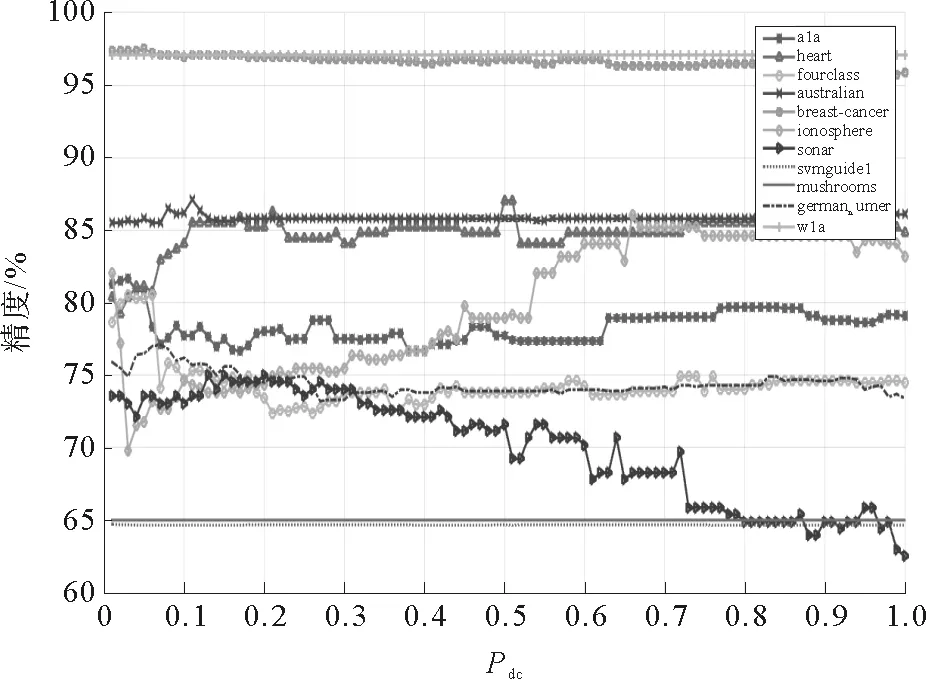
图8 Pdc取值变化对分类精度的影响Fig..8 Effect of change of Pdc onclassification accuracy

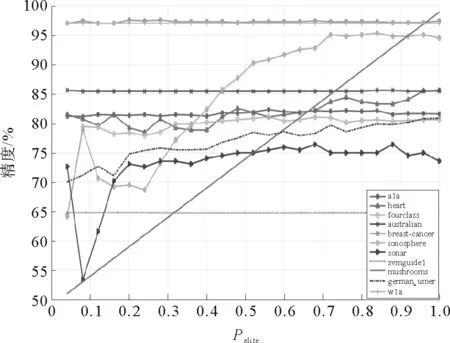
图9 Pelite取值变化对分类精度的影响Fig.9 Effect of change of Peliteon classification accuracy

4 结语

本文给出了一种新的样本点选取标准，并基于该标准设计实现了一种适用于不同分类器的样本约简算法。与其他算法相比较，该算法可以根据需求获得任意大小的样本子集。与多种分类算法进行测试对比，算法的约简效果综合指标要优于其他算法。对包含噪声点的样本集，算法的分类精度和稳定性均有一定程度的提高。在模式挖掘中使用该算法，可以提高模式挖掘效率。如何针对大数据做并行化改进，是下一步需要研究的问题。

[1]WILSONDL.Asymptoticpropertiesofnearestneighborrulesusingediteddata[J].IEEETransactionsonSystemsMan&Cybernetics,1972,2(3):408-421.

[2]WILSONDR,MARTINEZTR.Reductiontechniquesforinstance-basedlearningalgorithms[J].MachineLearning,2000,38(3):257-286.

[3]TOMEKI.Anexperimentwiththeeditednearest-neighborrule[J].IEEETransactionsonSystemsMan&Cybernetics,1976,SMC-6(6):448-452.

[4]HARTP.Thecondensednearestneighborrule[J].IEEETransactionsonInformationTheory,1968,14(3):515-516.

[5]GATESG.Thereducednearestneighborrule[J].IEEETransationsonInformationTheory,1972,18(3):431-433.

[6]DASARATHYBV.Minimalconsistentset(MCS)identificationforoptimalnearestneighbordecisionsystemsdesign[J].IEEETransactionsonSystemsMan&Cybernetics,1994,24(3):511-517.

[7]ANGIULLIF.Fastnearestneighborcondensationforlargedatasetsclassification[J].IEEETransactionsonKnowledgeandDataEngineering,2007,19(11):1450-1464.

[8]BRIGHTONH,MELLISHC.Advancesininstanceselectionforinstance-basedlearningalgorithms[J].DataMining&KnowledgeDiscovery,2002,6(2):153-172.

[9]WILSONDR,MARTINEZTR.Reductiontechniquesforinstance-basedlearningalgorithms[J].MachineLearning,2000,38(3):257-286.

[10]REINARTZT.Aunifyingviewoninstanceselection[J].DataMining&KnowledgeDiscovery,2002,6(2):191-210.

[11]GARCIAS,DERRACJ,CANOJR,etal.Prototypeselectionfornearestneighborclassification:Taxonomyandempiricalstudy[J].IEEETransactionsonPatternAnalysis&MachineIntelligence,2012,34(3):417-435.

[12]CHENJ,ZHANGC,XUEX,etal.Fastinstanceselectionforspeedingupsupportvectormachines[J].Knowledge-BasedSystems,2013,45(3):1-7.

[13]WANGXZ,DONGLC,YANJH.Maximumambiguity-basedsampleselectioninfuzzydecisiontreeinduction[J].IEEETransactionsonKnowledge&DataEngineering,2012,24(8):1491-1505.

[14]HAMIDZADEHJ,MONSEFIR,YAZDIHS.LMIRA:Largemargininstancereductionalgorithm[J].Neurocomputing,2014,145(18):477-487.

[15]HAMIDZADEHJ,MONSEFIR,YAZDIHS.IRAHC:Instancereductionalgorithmusinghyperrectangle[J].PatternRecognition,2015,48(5):1878-1889.

[16]NIKOLAIDISK,RODRIGUEZ-MARTINEZE,GOULERMASJY,etal.Spectralgraphoptimizationforinstancereduction[J].IEEETransactionsonNeuralNetworks&LearningSystems,2012,23(7):1169-1175.

[17]GARCIA-LIMONM,ESCALANTEHJ,MORALES-REYESA.IndefenseofonlineKmeansforprototypegenerationandinstancereduction[C]//ACMConferenceonComputerSupportedCooperativework,CSCW2004,Chicago,2016:274-283.

[18]JAMJOOMM,HINDIKE.Partialinstancereductionfornoiseelimination☆[J].PatternRecognitionLetters,2016,74:30-37.

[19]RODRIGUEZA,LAIOA.Clusteringbyfastsearchandfindofdensitypeaks[J].Science,2014,344 (6191):1492-1496.

[20]LEWISDD,GALEWA.Asequentialalgorithmfortrainingtextclassifiers[C]//AcmSigirForum.Springer-VerlagNewYork,Inc.1994:3-12.

[21]SETTLESB.Activelearningliteraturesurvey[J].UniversityofWisconsinmadison,2010,39(2):127-131.

[22]DAGANI,ENGELSONSP.Committee-basedsamplingfortrainingprobabilisticclassifiers[J].MachineLearningProceedings,1995:150-157.

[23]SUYKENSJAK,VANDEWALLEJ.Leastsquaressupportvectormachineclassifiers[J].NeuralProcessingLetters,1999,9(3):293-300.

[24]THOTK,KLEINBERGEM.Buildingprojectableclassifiersofarbitrarycomplexity[C]//InternationalConferenceonPatternRecognition.IEEEComputerSociety,1996:880.

[25]HSUCW,CHANGCC,LINCJ.Apracticalguidetosupportvectorclassification[R].Taiwan:NationalTaiwanUniversity.

[26]PLATTJC.Fasttrainingofsupportvectormachinesusingsequentialminimaloptimization[C]//AdvancesinKernelMethods-supportVectorRning.MITPress,1999:185-208.

(责任编辑：傅 游)

An Instance Reduction Algorithm for Different Classifiers

CHENG Rufeng,LIANG Yongquan,LIU Tong

(College of Computer Science and Engineering,Shandong University of Science and Technology,Qingdao,Shandong 266590,China)

Most of the existing instance reduction algorithms are designed for particular classifiers,which have some limitations in practical application.Combined with the idea of clustering algorithm,this paper proposes an instance reduction algorithm applicable to different classifiers.The core idea is to select instances with high density and relatively far distance.Compared with other instance reduction algorithms,this algorithm can obtain the instance subset in any size and can be applied to a variety of classification algorithms.For the set with noise,both the classification accuracy and stability of the proposed algorithms can be improved to some extent.

instance reduction; criterion; density; instance subset

2016-10-12

山东省高等学校科技计划项目(J14LN33)；中国博士后科学基金项目(2014M561949)；2014青岛市博士后项目；山东科技大学研究生科技创新项目(SDKDYC170340)

程汝峰(1992—),男,山东德州,硕士研究生,主要从事数据挖掘与机器学习研究． 梁永全(1968—),男,山东聊城,教授,博士生导师,主要从事分布式人工智能、数据挖掘与机器等的学习研究,本文通信作者．E-mail：lyq@sdust.edu.cn

TP181

A

1672-3767(2017)03-0114-09