离散多时滞系统鲁棒渐近稳定性分析-扩展反凸组合法
2017-06-01魏清泉夏建伟
魏清泉,夏建伟
(1.山东省聊城市第二中学,山东 聊城 252000;2.聊城大学 数学科学学院,山东 聊城 252000)
离散多时滞系统鲁棒渐近稳定性分析-扩展反凸组合法
魏清泉1,2,夏建伟2
(1.山东省聊城市第二中学,山东 聊城 252000;2.聊城大学 数学科学学院,山东 聊城 252000)
研究了一类带有多区间时变时滞不确定离散系统的鲁棒渐近稳定性问题,其中不确定参数满足线性分式结构。首先, 将Reciprocally convex方法推广到离散系统,得出一个新的有界引理;并基于该引理,得到具有更小保守性的时滞相关稳定条件;最后,给出一些数值仿真实例证明所提方法的有效性。
不确定离散系统; 鲁棒渐近稳定性; 多时滞系统;凸组合;时变时滞
时滞广泛存在于众多实际控制系统, 也是引起系统失稳、振荡及性能差的重要原因之一,近几十年中, 时滞系统稳定性分析问题得到了大量学者的关注[1-4]。 根据是否考虑时滞之间的关系, 时滞稳定条件可分为两大类:时滞无关稳定条件和时滞相关稳定条件。 前者对于时滞大小没有要求, 后者考虑了时滞大小对稳定性的影响, 一般来讲, 时滞相关稳定条件比时滞无关稳定条件具有更小的保守性。 因此, 寻找保守性小且易于验证的时滞相关条件, 成为近年来时滞系统稳定性分析理论研究的一个非常活跃的分支, 涌现出诸多有效的方法,如积分不等式法[5]、时滞分割法[6]、凸组合法[7]、自由权矩阵法[8]和Wirtinger积分不等式法[9]等。
同时,由于离散系统在工程过程监控、故障诊断等工程领域得到广泛应用, 使得对离散系统的分析与综合研究具有很强的实际意义,许多连续系统的结论也相应的推广到离散系统,离散时滞系统的稳定性研究得到大量关注,[10-14]。 但现有文献中,多时滞离散系统的稳定性问题的研究较少。近年来,仅有文献[15-17]对几类带有多时滞离散系统的渐近稳定和镇定性等问题进行了研究,但处理时滞积分交叉项所用方法均为詹森不等式和自由权矩阵方法,这导致结果具有较大保守性。对带有多时滞的离散系统,获得保守性更小的时滞相关稳定性结果仍有很大的研究空间。
本文研究了一类带有多区间时变时滞的离散系统的鲁棒渐近稳定性问题, 通过扩展的Reciprocally convex方法, 得到一个针对离散时滞系统稳定性分析更有效的积分不等式引理。在新的引理基础上,针对带有多时滞离散系统的两种不同参数不确定情况,给出了新的时滞相关稳定条件。最后,给出几个数值仿真实例,说明本文所得结果较已有相关结果具有更小的保守性。
1 系统描述和预备知识
考虑下面带有多区间时变时滞的不确定离散系统:

(1)
x(k)=φ(k),k=-h,-h+1,…,0;
(2)
其中:x∈Rn是状态变量;实数hi(k)是时变延迟满足0≤h1i≤hi(k)≤h2i,i=1,2,…,m,h1i,h2i是非负整数,且h=max{h21,h22,…,h2m};φ(k)是系统(1)~(2)在初始条件下的值;Ai(k)是时变矩阵,并具有如下形式的时变不确定性:
Ai(k)=Ai+ΔAi(k),
(3)
且不确定性ΔAi(k)具有如下线性分式结构:
ΔAi(k)=LAΔ(k)EAi;
(4)
Δ(k)=[I-F(k)J]-1F(k);
(5)
I-JJΤ>0。
(6)
其中,J,LA,EAi是已知常数矩阵,未知矩阵F(k)是勒贝格可测因子,并且满足
FΤ(k)F(k)≤I。
(7)
注1:如果J=0,假设Δ(k)=F(k)满足FT(k)F(k)≤I,则不确定性ΔAi(k)将变成范数有界形式:
ΔAi(k)=LAF(k)EAi。
(8)
引入下面引理:
引理1[18]对于任意常数矩阵H∈Rm×m,H=HΤ>0,整数l1,l2满足l1 (9) 引理2[20]给定矩阵M,S,N,且M=MΤ,若存在实数δ>0,有矩阵不等式 (10) 成立,那么对于任意满足条件(5)~(7)的Δ(k),都有M+SΔ(k)N+NΤΔ(k)SΤ<0。 (11) (12) (13) 证明:运用引理1,有 (14) (15) (16) (17) 其中Ωi,di定义于(13)式,证毕。 注2:反凸组合法作为一种有效降低结果保守性的工具,已经广泛应用到研究各类时滞系统的稳定性问题[1,4],但文献[1,4]中的方法仅仅适用于连续时滞系统。本文将Reciprocally convex方法推广到离散的情况,这将帮助得到多区间时变时滞离散系统的新的时滞相关稳定条件,且具有更小的保守性。 为简便,定义变量: χ(k) =[xΤ(k)xΤ(k-h11)xΤ(k-h1(k))xΤ(k-h21) …xΤ(k-h1m)xΤ(k-hm(k) xΤ(k-h2m)yΤ(k)]Τ, (18) 可以得到系统具有线性分式形式不确定性的鲁棒渐近稳定条件,即定理1。 (19) 则系统(1)~(2)是鲁棒渐近稳定的。其中 (20) 证明 一方面,根据引理2.2,由(19)式,可得: (21) 另一方面,选取如下李雅普诺夫泛函: (22) 其中: 假设y(k)=x(k+1)-x(k)。定义ΔV(k)=V(k+1)-V(k)。则: (24) 根据引理1,有: (25) (26) 同时,注意到: (27) 式(27)可改写为: (28) 由式(24)~(28)可得: ΔV(k)≤χΤ(k)Ξχ(k)。 (29) 当不确定性满足(8)范数有界形式时,有下面定理: (30) 则系统(1)~(2)是鲁棒渐近稳定的。其中 (31) 其中Ωi定义于(13)。 证明 一方面,对(30)式运用Schur补引理,则有 (32) 另一方面,类似定理2.1证明,可得结论。 在本文中,为了与已有结果进行比较,在系统(1)~(2)中,令m=1,得到下面系统: x(k+1)=A0(k)x(k)+A1(k)x(k-h1(k)), (33) x(k)=φ(k),k=-h2,-h2+1,…,0。 (34) 那么分别根据定理1和定理2,易得下面推论1和推论2。 (35) 则系统(33)~(34)是鲁棒渐近稳定的。其中 Λ22=-R11-Z-S,Λ23=Z-U,Λ24=U,Λ25=0,Λ33=-Q-2Z+U+UΤ,Λ34=-U+Z, (36) 则系统(33)~(34)是鲁棒渐近稳定的。其中: 推论1和推论2可由以上两个定理推得,证明过程在此不再赘述。 例1 根据定理1,考虑系统(1)~(2),取m=2和下面系统参数: 表1 不同的h12所对应的h22的上界值 通过求解LMI(19),取定h1(k)、h2(k)的下界,令h11=1,h21=2,对于不同的h12,可得h22的上界与之对应,见表1。 例2 根据定理2,考虑系统(1)~(2),取m=2和下面系统参数: 取不同的h12所对应的的h22上界值,见表2。 表2 不同的h12所对应的h22的上界值 例3 根据推论2,考虑系统(33)~(34),取文献[19]定理2 的系统参数: 方法h1,h2[][6,12][10,15][20,25][30,35]推论2α0.22560.17280.11300.1008[19]α0.13210.11210.09370.0920[18]α0.11460.10230.0886— 注3 由表3可知,本文所用的方法比文献[18-19]允许更高的扰动,因而验证了本文方法所得结果具有更小的保守性。 研究了一类多区间时变时滞不确定离散系统的鲁棒渐近稳定性问题,将Reciprocallyconvex方法推广到离散系统,得到一个新的积分不等式引理,根据不同的不确定性形式,得到具有更小保守性的时滞相关稳定条件。最后,数值仿真实例说明了方法的有效性。 [1]WUZ,LAMJ,SUH,Stabilityanddissipativityanalysisforstaticneuralnetworkswithtimedelay[J].IEEETransactionsonNeuralNetwork, 2012,23:199-210. [2]XIAJ,SUNC,ZHANGB.NewrobustH∞controlforuncertainstochasticMarkovianjumpingsystemswithmixeddelaysbasedondecouplingmethod[J].JournaloftheFranklinInstitute,2012,349(3):741-769. [3]YANGR,ZHANGZ,SHIP.Exponentialstabilityonstochasticneuralnetworkswithdiscreteintervalanddistributeddelays[J].IEEETransactionsonNeuralNetworks, 2010, 21(1):169-175. [4]XIAJ,Park,J,ZENGH.Delay-different-dependentrobustexponentialstabilityforuncertainstochasticneuralnetworkswithtime-varyingdelays[J].Neurocomputing,2014,140:210-218. [5]HEY,WANGQ,LINC,etal.Delay-rang-dependentstabilityforsystemswithtime-varyingdelay[J].Automatica, 2007, 43(2):371-376. [6]WUH,WANGJ,SHIP.AdelaydecompositionapproachtoL2-L∞filterdesignforstochasticsystemswithtime-varyingdelay[J].Automatica, 2011, 47(7):1482-1488. [7]PARKPG,KOJW,JEONGC.Reciprocallyconvexapproachtostabilityofsystemswithtime-varyingdelays[J].Automatica, 2011,47(1):235-238. [8]吴敏,何勇.时滞系统鲁棒控制[M].北京:科学出版社,2008. [9]SEURETA,GOAISBAUTF.Wirtinger-basedintegralinequality:Applicationtotime-delayssystems[J].Automatica,2013, 49:2860-2866. [10]GAOM,CUIB.Globalrobustexponentialstabilityofdiscrete-timeintervalBAMneuralnetworkswithtime-varyingdelays[J].Appl.Math.Model[J].2009,33(3):1270-1284. [11]KIMJH.Delay-dependentrobustH∞filteringforuncertaindiscrete-timesingularsystemswithintervaltime-varyingdelay[J].Automatica,2010,46(3):591-597. [12]郑连伟,宋叔尼,戴良萃.不确定线性离散时滞系统的稳定性[J].东北大学学报,2013,34(12):1691-1694.ZHENGLianwei,SONGShuni,DAILiangcui.Exponentialstabilityforuncertainlineardiscrete-timesystemswithtime-varyingdelays[J].JournalofNortheasternUniversity,2013,34(12):1691-1694. [13]李阳,赵晓颖,张钟元.基于LMI的范数有界不确定仿射离散时滞系统的鲁棒控制[J].西安工程大学学报,2012,26(5):629-632.LIYang,ZHAOXiaoying,ZHANGZhongyuan.LMIbasedrobustcontrolofnorm-boundeduncertainaffineddiscretesystemswithstatedelay[J].JournalofXi’anPolytechnicUniversity,2012,26(5):629-632. [14]XIANGM,XIANGZ,Exponentialstabilityofdiscrete-timeswitchedlinearpositivesystemswithtime-delay[J].AppliedMathematicsandcomputation.2014, 230(3):193-199. [15]SYEDAM,P.Globalasymptoticstabilityofstochasticfuzzycellularneuralnetworkswithmultiplediscreteanddistributedtime-varyingdelays[J].CommunicationsinNonlinearScienceandNumericalSimulation.2011, 16(7):2907-2916. [16]BENZAOUIAA,OUBAHR,HAJJAJIAE.StabilizationofpositiveTakagi-Sugenofuzzydiscrete-timesystemswithmultipledelaysandboundedcontrols[J].JournaloftheFranklinInstitute,2014,35(7):3719-3733. [17]ZHANGJ,ZHANGH,LUOY,Model-freeoptimalcontroldesignforaclassoflineardiscrete-timesystemswithmultipledelaysusingadaptivedynamicprogramming[J].Neurocomputing,2014,135(8):163-168. [18]HUANGH,FENGG.Improvedapproachtodelay-dependentstabilityanalysisofdiscrete-timesystemswithtime-varyingdelay[J].IETControlTheoryA.2010, 4(10):2152-2159. [19]RAMAKRISHNANK,RAYG.Robuststabilitycriteriaforaclassofuncertaindiscrete-timesystemswithtime-varyingdelay[J].AppliedMathenaticsandComputerScience,2013,37(3):1468-1479. [20]LIT,GUOL,LINC.Anewcriterionofdelay-dependentstabilityforuncertaintime-delaysystems[J].IETControlandApplications,2007,1(3):611-616. (责任编辑:傅 游) Robust Asymptotical Stability Criteria for Discrete-time System with Multiple Interval Time-varying Delays Based on Extended Reciprocal Convex Approach WEI Qingqun1,2, XIA Jianwei2 (1. No. 2 Senior Middle School of Liaocheng, Liaocheng, Shandong 252000, China; 2. College of Mathematical Sciences, Liaocheng University, Liaocheng, Shandong 252000, China) The paper studies the problem of robust asymptotical stability for a class of uncertain discrete-time system with multiple interval time-varying delays, in which the uncertain parameters are in linear fractional form. Firstly, a new integral bound lemma was derived by extending the reciprocal convex approach to discrete system. Then, the novel delay-dependent stability criteria with less conservatism was obtained based on the lemma. Finally, numerical examples were given to show the effectiveness of the proposed methods. uncertain discrete-time system; robust asymptotical stability; multiple delays; reciprocal convex; time-varying delay 2016-10-08 国家自然科学基金项目(61573177) 魏清泉(1974—),男,副教授,主要从事时滞系统稳定性分析方面的研究工作.E-mail:qingquanwei@163.com O231.3 A 1672-3767(2017)03-0096-08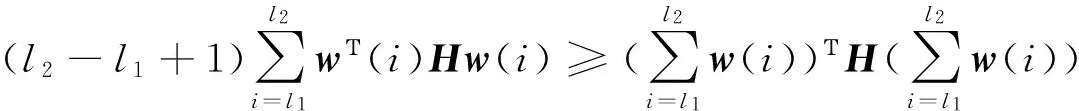
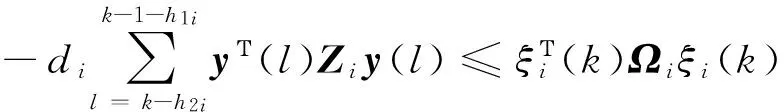



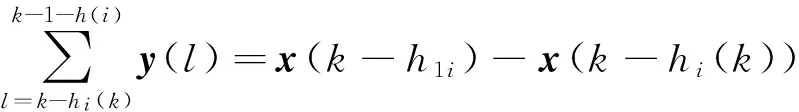

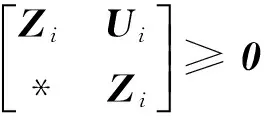
2 主要结果



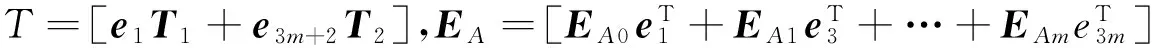
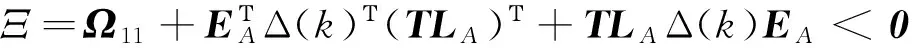
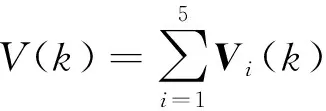
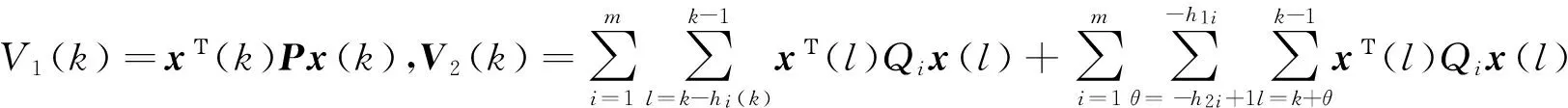
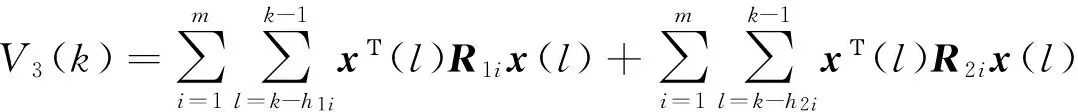
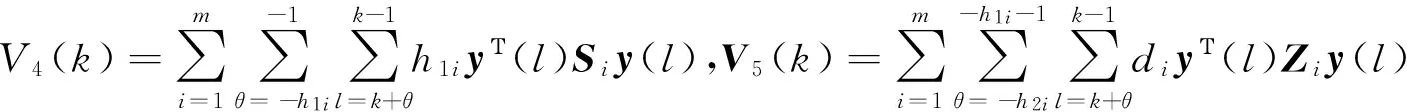





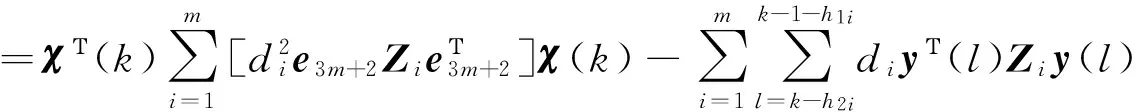


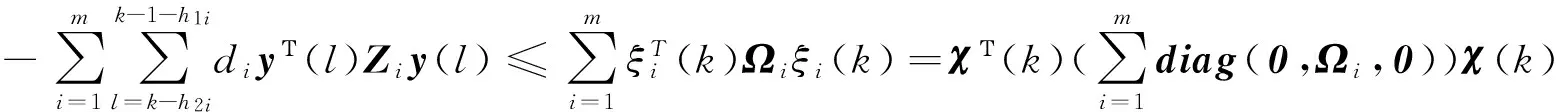





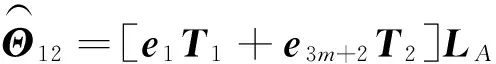
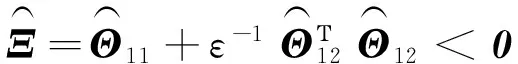







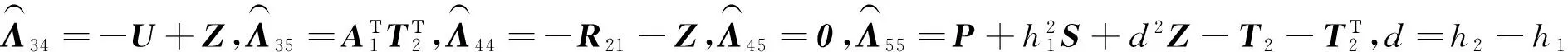
3 数值实例




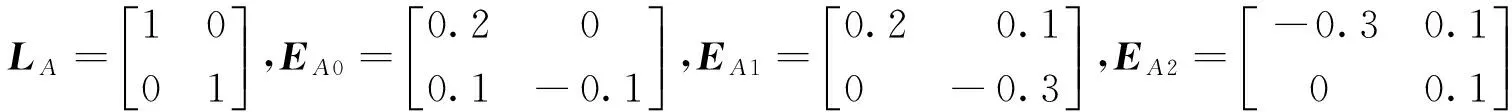


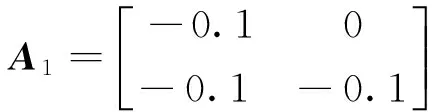




4 结论
