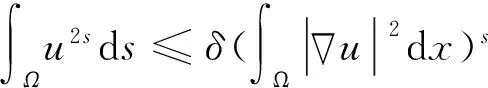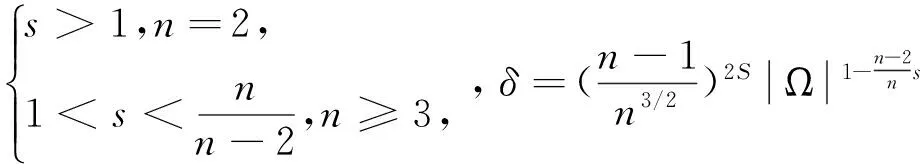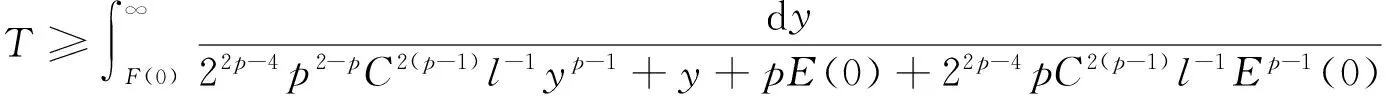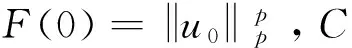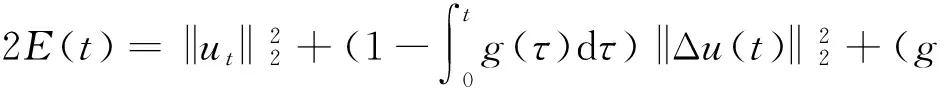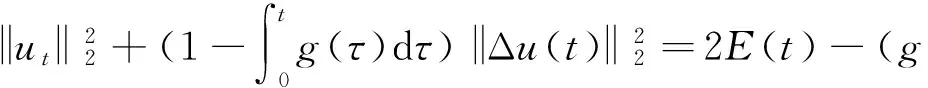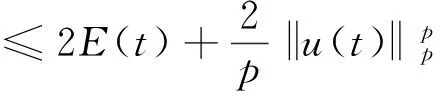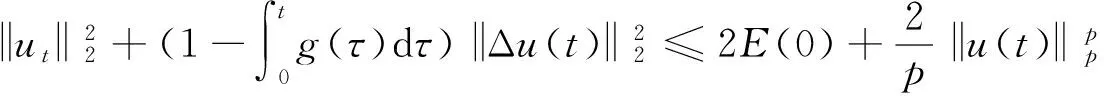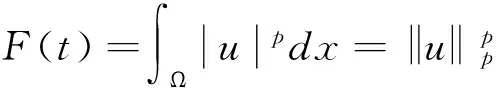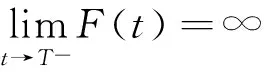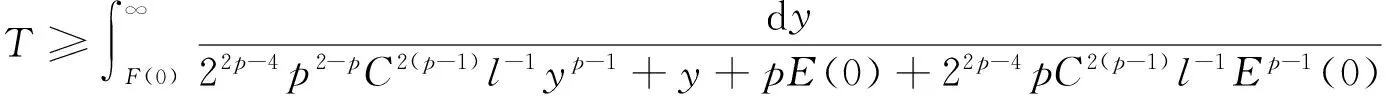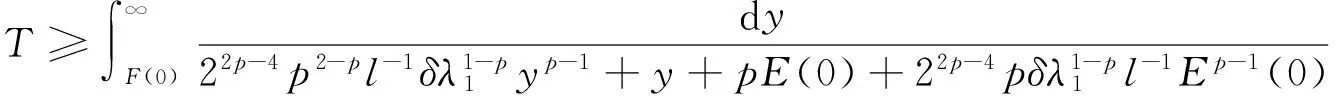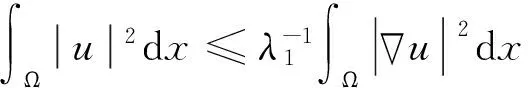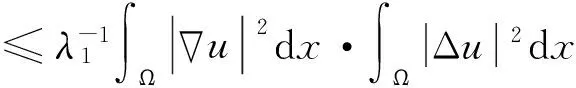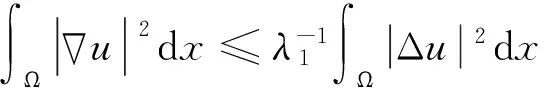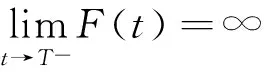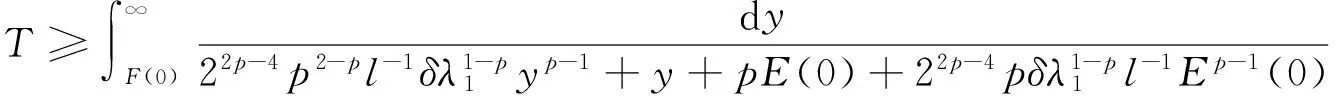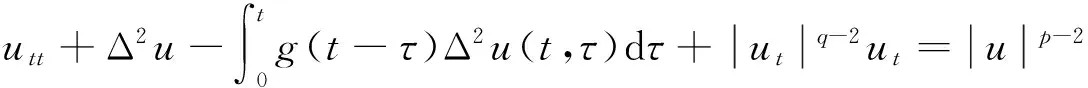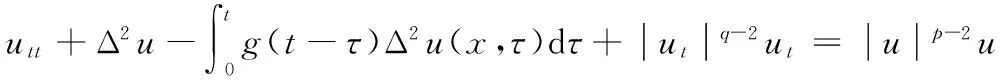一类带记忆项的非线性Petrovsky方程解的爆破时间下界估计
2017-06-01胡文燕柴树根
胡文燕,柴树根
(1.晋中学院 数学学院,山西 晋中 030600;2.山西大学 数学科学学院,山西 太原 030006)
一类带记忆项的非线性Petrovsky方程解的爆破时间下界估计
胡文燕1,柴树根2
(1.晋中学院 数学学院,山西 晋中 030600;2.山西大学 数学科学学院,山西 太原 030006)
考虑如下具有记忆项的非线性Petrovsky方程:
非线性Petrovsky方程;记忆项;正的初始能量;爆破时间;下界估计
考虑如下带记忆项的非线性Petrovsky方程的初边值问题:
(※)
对于不带记忆项的Petrovsky方程:
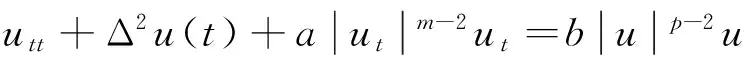
(1)
文献[1]证得当m 因为当爆破发生时,精确的爆破时刻往往是无法估算的,从而研究爆破时刻的上下界就变得非常重要。很多学者已经对拋物型方程的爆破时刻的下界估计做了大量研究,并得出了相应的结果[4-10]。文献[11]对如下不带记忆项的Petrovsky方程进行了研究: (2) 并给出了该方程在正的初始能量下解的爆破时间下界估计。 对于具有记忆项的Petrovsky方程: (3) 文献[12]研究了其解的局部存在性,给出了当初始能量有上界时解在有限时间内会爆破的结论。 本文在前人工作基础上,进一步对具有记忆项的Petrovsky方程解的爆破时间进行研究,并给出了在正的初始能量下解的爆破时间的下界估计。 考虑Lebesgue空间Lp(Ω)和Sobolev空间Hq(Ω),对于不增的松弛函数g(t),假设如下: (I1)g:R+→R+满足: (4) 且 (5) g′(t)≤0,t≥0。 (6) (7) (8) ut∈C([0,T];L2(Ω))∩Lq(Ω×(0,T)); utt∈L∞((0,T);L2(Ω))。 证明 可以利用Faedo-Galerkin方法,证明其解的存在性和唯一性(参考文献[1])。 (9) 其中C为Sobolev嵌入的最佳常数。 再由Poincaré不等式可得 证毕。 定义初边值问题(※)的能量函数E(t)如下: (10) 其中(g。 引理1.2[12]假设g,p,q分别满足(I1),(I2),(I3),且u(t)为初边值问题(※)的解,那么 证明 将初边值问题(※)的方程两边同乘以ut,并在Ω上积分,运用格林公式,可得 (11) 其中, (12) 将(12)代入(11),由g′(t)≤0,有 即E′(t)≤0,证毕。 定理1.2[12]假设g,p,q满足条件(I1),(I2),(I3),那么当p>q,且E(0) 详细证明过程见参考文献[12]。 引理2.1[13]若Ω⊂R2(n≥2)为一光滑区域,当x∈Ω时,u(x)为一分段函数,当x∈∂Ω时,u(x)≡0,则下述不等式成立: 定理2.2 若u为问题(※)的解,它在有限时刻T爆破,则 证明 由能量函数(10)式,有 那么 由引理1.2,E′(t)≤0,即E(t)≤E(0),将其代入上式可得 (13) =22p-4p2-pC2(p-1)l-1Fp-1(t)+F(t)+pE(0)+22p-4pC2(p-1)l-1Ep-1(0)。 (14) 在定理2.1中,由于C并不是一个确切的值,故很难找到爆破时间T的准确下界,为此,假设p满足: (15) 显然,在此假设条件(I2)仍成立。 定理2.3 假设m,q满足(I1),(I3),p满足(15)式,若u(x,t)为问题(※)的解,它在有限时刻T爆破,则 证明 因为λ1>0为齐次Dirichlet边界条件下的第一特征值,所以 由Hölder不等式,有 即 由引理2.1,取s=p-1,可得 证毕。 [1]MESSAOUDISA.GlobalexistenceandnonexistenceinasystemofPetrovsky[J].JournalofMathematicalAnalysis&Applications,2002,265(2):296-308. [2]MESSAOUDISA.GlobalexistenceanddecayofsolutionstoasystemofPetrovsky[J].MathematicalSciencesResearchJournal,2002,6(11):534-541. [3]CHENW,ZHOUY.GlobalnonexistenceforasemilinearPetrovskyequation[J].NonlinearAnalysis,2009,70(9):3203-3208. [4]BAGHAEIK,HESAARAKIM.Lowerboundsfortheblow-uptimeinthehigher-dimensionalnonlineardivergenceformparabolicequations[J].ComptesRendusdel′Académie,2013,351(19):731-735. [5]BAOA,SONGX.Boundsfortheblowuptimeofthesolutionstoquasi-linearparabolicproblems[J].ZeitschriftfurAngewandteMathematikundPhysik,2014,65(1):115-123. [6]LIUY,LUOS,YEY.Blow-upphenomenaforaparabolicproblemwithagradientnonlinearityundernonlinearboundaryconditions[J].Computers&MathematicswithApplications,2013,65(8):1194-1199. [7]LIUY.Blow-upphenomenaforthenonlinearnonlocalporousmediumequationunderRobinboundarycondition[J].Computers&MathematicswithApplications,2013,66(10):2092-2095. [8]LIUY.Lowerboundsfortheblow-uptimeinanon-localreactiondiffusionproblemundernonlinearboundaryconditions[J].MathematicalandComputerModelling,2013,57(3):926-931. [9]PAYNELE,PHILIPPINGA.Blow-upphenomenainparabolicproblemswithdependentcoefficientsunderDirichletboundaryconditions[J].ProceedingsoftheAmericanMathematicalSociety,2013,141(7):2309-2318. [10]SONG J C.Lower bounds for the blow-up time in a non-local reaction-diffusion problem[J].Applied Mathematics Letters,2011,24(5):793-796. [11]ZHOU J.Lower bounds for blow-up time of two nonlinear wave equations[J].Applied Mathematics Letters,2015,45(2) :64-68. [12]LI F S,GAO Q Y.Blow-up of solution for a nonlinear Petrovsky type equation with memory[J].Applied Mathematics and Computation,2016,274(2):383-392. [13]PHILIPPIN G A.Lower bounds for blow-up time in a class of nonlinear wave equation[J].Zeitschrift Fur Angewandte Mathematik und Physik,2015,66(1):129-134. (责任编辑:傅 游) Lower Bounds for Blow-up Time of a Nonlinear Petrovsky Equation with Memory HU Wenyan1,CHAI Shugen2 (1.School of Mathematics,Jinzhong University,Jinzhong,Shanxi 030600,China; 2.School of Mathematical Sciences,Shanxi University,Taiyuan,Shanxi 030006,China) nonlinear Petrovsky equation; memory; positive initial energy; blow-up time; lower bounds 2016-09-12 国家自然科学基金项目(11171195) 胡文燕(1983—),女,山西平遥人,讲师,研究方向为偏微分方程.E-mail:huwy0007@163.com柴树根(1969—),男,山西介休人,教授,博士生导师,主要从事应用数学研究. O A 1672-3767(2017)03-0091-05 具Dirichlet边界条件的初边值问题。当松弛函数g满足适当的条件时,该问题的解在有限时间内会爆破。进一步对解的爆破时间进行研究,给出了正的初始能量下解的爆破时间的下界估计。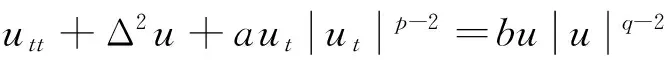
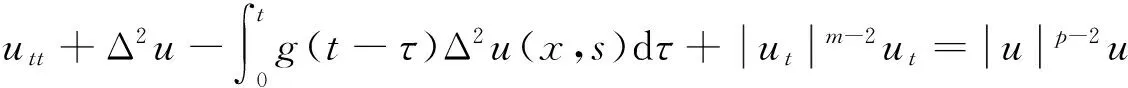
1 预备知识
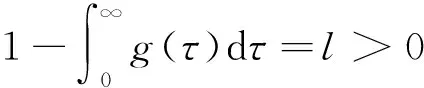
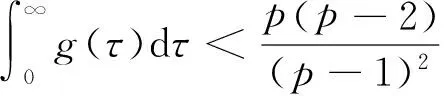

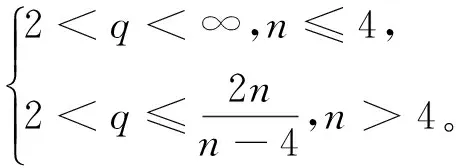

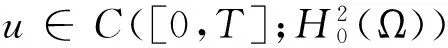
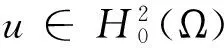

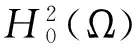
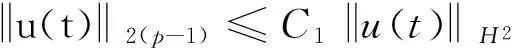

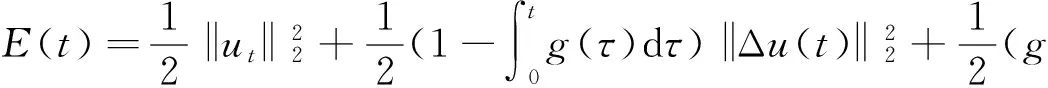
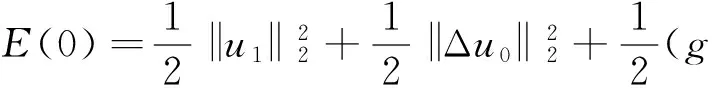

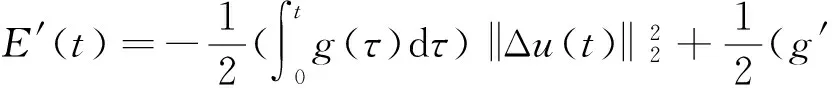
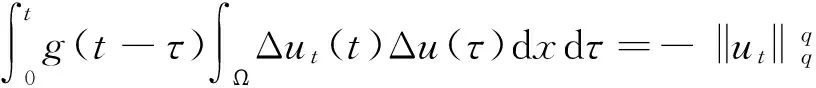
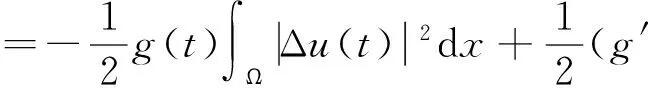
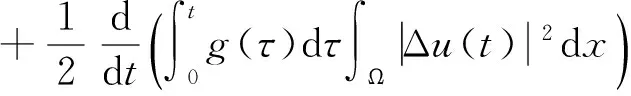
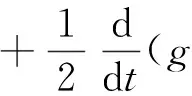
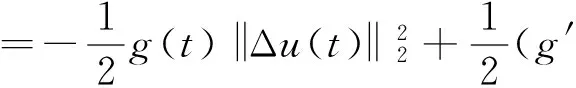
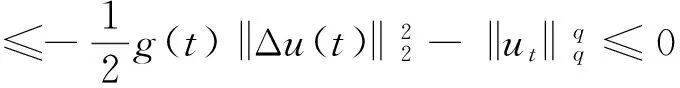

2 主要结果及证明