端部撞击下内充压力介质悬臂管道瞬态动力响应研究
2017-06-01吴月磊孟凡俭
刘 锋,吴月磊,张 航,孟凡俭
(1.山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590;2.同济大学 土木工程防灾国家重点实验室,上海 200092)
端部撞击下内充压力介质悬臂管道瞬态动力响应研究
刘 锋1,2,吴月磊1,张 航1,孟凡俭1
(1.山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590;2.同济大学 土木工程防灾国家重点实验室,上海 200092)
针对管道甩动问题,考虑介质和内充压力的影响,基于变形后的线元模型,推导了管道动力响应的大变形控制方程。考虑到悬臂结构的响应特点,本构方程解耦弯矩和轴力,并采用实验测量的弯矩-曲率关系描述管道弯曲行为。数值研究表明,此模型可以准确模拟管道响应过程中的初始弹性、中期塑性强化、后期软化力学过程。强动载荷作用下,悬臂空管道会因某些截面的局部失效而在整体管段上形成“结节”,表现出实腹式截面未曾出现的“软化”行为。内充介质和压力的存在可以有效抵抗管道截面的局部扁平化趋势,提高管道截面的临界曲率,从而改变其塑性动力响应行为。
充压管道;介质;内压;撞击;塑性强化-软化行为
输送高能、高压流体的管道广泛应用于核电站及各类石油化工设施中。在偶然撞击或其他强动载荷作用下,此类构件会产生大变形弯曲或动力失效,进而引发灾难性连锁反应。有典型工程案例即为偶然撞击引发高压管道破裂,内充压力介质逃逸引起管道大变形甩动,并因不规则撞击导致附近更大范围内管道失效[1-2]。
薄壁圆管的弯曲行为可能包含两种变形机制。其一是随着弯矩增大,管道截面由初始的圆形向椭圆形发展,并最终形成扁平状。形状的变化将导致抗弯刚度下降,使其抗弯能力在某一临界曲率后急剧下降,并迅速失去承载能力。此现象由Brazier首先发现,因此常被称为“Brazier”效应[3],对应于普遍熟知的弹性-塑性强化现象,此过程被研究者称为“软化”行为[4]。其二即为在管道截面的受压侧发生因压应力过大引发管壁屈曲。Yu[3]、Reid[4-5]、Prinja[6]等的实验研究真实记录了悬臂管梁在变形过程中由于个别截面超越临界曲率后出现的“软化”行为。基于对空管道四点弯曲实验所得的弯矩-曲率关系以及引入基于广义本构方程的大挠度控制方程,Reid等[5]对该悬臂空管道的弹塑性动力响应进行了数值模拟,重演了该类管道在介质逃逸所引发的甩动载荷下,因局部截面软化所出现的“结节”现象。
值得注意的是,为了简化问题,针对悬臂管道动力响应的少量实验和理论研究工作[4]均忽略管道内必然存在的介质和压力。实际上,在针对两端固支管道冲击力学行为的实验研究中,Norman[2], Palmer[7]以及Nishida[8]等发现,无论充压与否,内充介质均引起相比空管道较小的局部变形。同时,Norman[2]、Qasim[9]和Lu[10]等对内充氮气和水、不同压力水平的管道进行的实验发现,压力水平的提高会使结构由撞击位置处的局部失效模式向整体失效模式转移,并引起失效能量降低。尽管基于不同实验设备和测试方法所得出的结论尚有相互矛盾之处,多种因素下管道动力失效的机理尚需进行更深刻的理解,但内充介质和压力会深刻影响管道的动力行为已不容置疑[2]。为了排除其他因素干扰,将研究重点局限于介质和压力对管道弯曲力学行为的研究,文献[11]针对空管道和多种压力水平下的内充水、空气、细沙的管道进行了系列静力四点弯曲实验。研究结果表明,介质的存在可能通过与管道内壁的相互作用抵制管道的局部变形,使其临界曲率和峰值弯矩高于空管道。此外,内充压力会引起管壁轴向和环向应力,从而有效提升管道的抗弯能力。
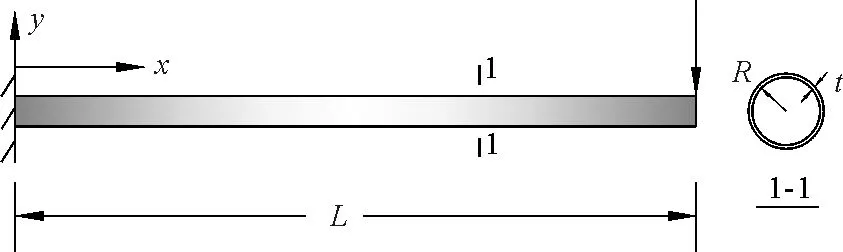
图1 端部承受集中撞击的悬臂充压管道Fig.1 Pressurized cantilever pipeline subjected to impact at its tip

图2 基于大变形构型的典型管道单元Fig.2 Typical element of structure under configuration of large deformation
悬臂管道在承受动力塑性弯曲时,固定边界处通常发生局部屈曲或截面形状畸变,惯性效应将显著影响其响应进程,内充压力介质的存在可能以何种方式和机制影响其动力行为?尽管此问题有强烈的工程背景,但迄今为止,尚未见有关此类问题的分析或实验。本研究基于针对内充压力介质管道进行的四点弯曲实验结果[11],考虑介质和内压影响,推导适应此问题的大变形控制方程,尝试应用简单梁单元对此类问题进行数值模拟。通过变形形态、曲率分布等变量的对比分析,探索内充介质和压力影响悬臂充压管道冲击动力行为的机理。
1 控制方程和求解
1.1 基本控制方程
考虑图2所示充压管道微段,由初始i*j*构型向ij变形发展,内力和变形对应关系为:
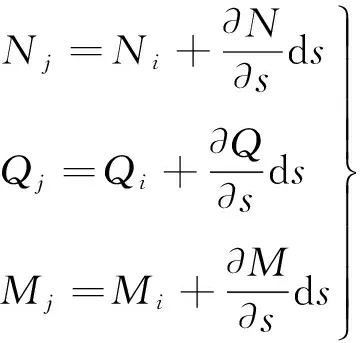
(1)
由微段的动平衡,可推导得到管段的运动学微分方程[12]

(2)

尽管机理尚未理解清楚,但实验研究表明,管内介质和压力会严重影响管道力学行为[2]。为考虑介质质量所引起的惯性力效应,式(2)中单位长度管段质量和转动惯量定义如下,
(3)
式中:D、d分别为管道外壁和内壁直径,ρp、ρm分别为管道和介质密度。
横向撞击下,结构动力响应过程始终伴随弯矩和轴力的耦合。但已有研究[4,12]表明,尽管悬臂结构在冲击动力响应下产生大变形,但其轴力在整个动力响应过程中始终维持较低水平,其最大数值不超过屈服轴力的10%,结构的整体响应主要由弯曲行为控制。基于此,解耦两变量,认为响应过程中弯矩和轴力相互独立,从而分别进行研究。
轴力N定义为
N=∫AσdA。
(4)
考虑内压的影响,管道截面轴向应力σ由初始介质压力引起的轴向应力σm和外部载荷引起的应力σI两部分组成,即:
σ=σm+σI;
(5)
σm=piRυ/t,σI=Eε;
(6)
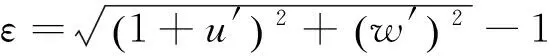
(7)
其中,pi、R、υ为管内压力、管道半径和管材泊松比。
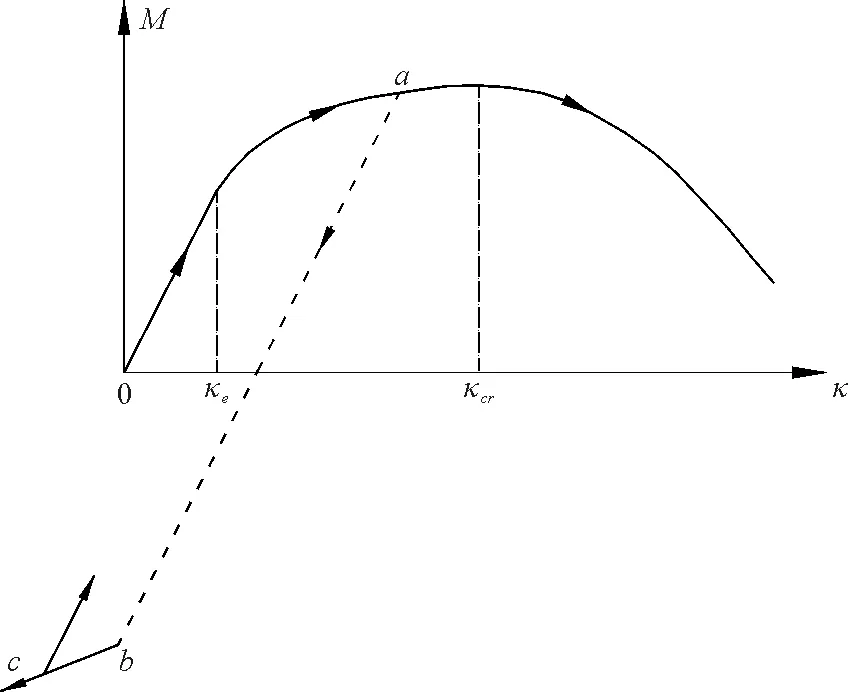
图3 考虑弹性-强化-软化效应的弯矩-曲率关系Fig..3 M-k curve for elastic,hardening-softeningbehaviour of pressurized pipe
同实腹式梁截面弯曲行为不同,薄壁管道的受弯过程包括截面的扁平化,以及更为复杂的局部截面崩溃引起的“软化”[3-4]。其过程涉及复杂的几何和材料非线性演变,通过针对实腹式梁截面式的应力分析方法难以准确把握[4]。故将管道纯弯实验[11]记录的真实截面弯矩-曲率关系引入动力方程,从而捕捉其复杂力学行为。图3所示为典型管道截面在纯弯作用下的弯矩-曲率关系,呈现典型的前期弹性-中期塑性强化-后期软化行为。为使问题分析简单化,规定数值计算中加、卸载路径分别遵守式(8)和(9)规则。
(8)
(9)

(10)
式中,κe、κcr分别为弹性、塑性强化、软化三阶段对应的临界曲率;κa、Ma为卸载开始时刻所对应的截面曲率和弯矩。
为使上述各方程得以求解,引入如下边界条件,
(11)

图4 离散状态的悬臂充压管道
Fig.4Discretemodelofcantileverpressurizedpipe
以上动力学控制方程,采用了基于变形后坐标描述的运动方程,考虑了管道内压的影响,引入了基于实验测量的弯矩-曲率关系,因而可以准确模拟充压管道在撞击荷载作用下的动力响应过程。
1.2 离散形式的控制方程与求解
为了求解控制方程,将图1所示悬臂管道沿轴向等分为n+1个微段,如图4所示。
控制方程式(2)的离散形式为:

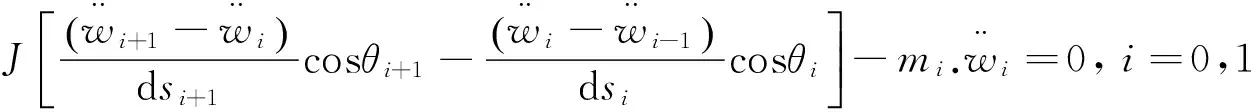
(12)
式中,
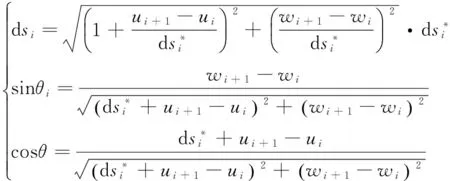
(13)
dsi为i微段变形后长度。
轴向应变和截面曲率的离散形式为,
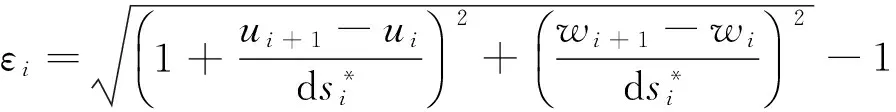
(14)
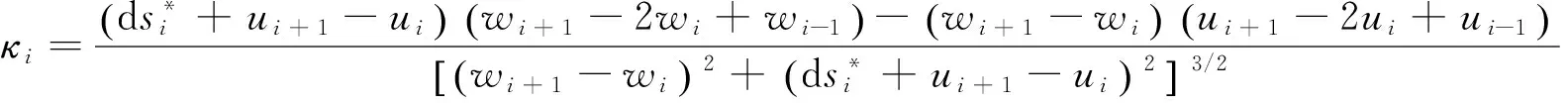
(15)
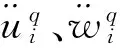

(16)
2 悬臂充压管道的弹塑性变形机制
为了考察弹塑性悬臂充压管道的变形机制,取文献[11]所述四点弯曲弯实验对应的试件参数进行分析。其中,试件直径D=25 mm,壁厚t=1 mm,长L=1.25 m。通过标准实验方法计算,确定材料弹性模量为208GPa,屈服强度480MPa,抗拉强度551MPa。
限于篇幅,除对比分析作用的空管道外,选取具有代表性的内充细沙(无内压)和充水(内压15MPa)管道进行数值分析,其截面弯矩-曲率关系如图5所示[11]。对应空管道及内充水(内压15MPa)、细沙三种工况,其截面塑性强化和软化行为的临界曲率分别为1.25、3.2和4.0m-1。此外,鉴于悬臂管道在撞击载荷作用下的实验研究报道较少,选取Reid等[4]针对空管道进行的甩动实验所实测的端部集中力为本研究的撞击荷载,其时间历程如图6所示。此外,为了考虑撞击块质量,数值计算中取重为1.0kg的质量块集中于悬臂端。通过试计算校核数值计算的稳定性,最终选取n=41,Δt=5.0 μs进行数值模拟。
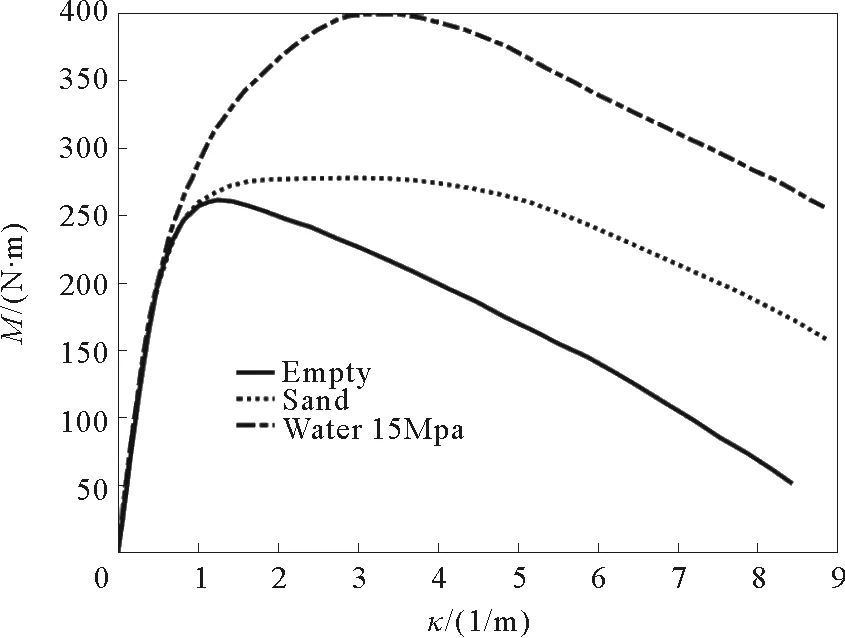
图5 实测管道弯矩-曲率关系[11]Fig..5 M-κ curve of pressurized pipe directly from experiment[11]
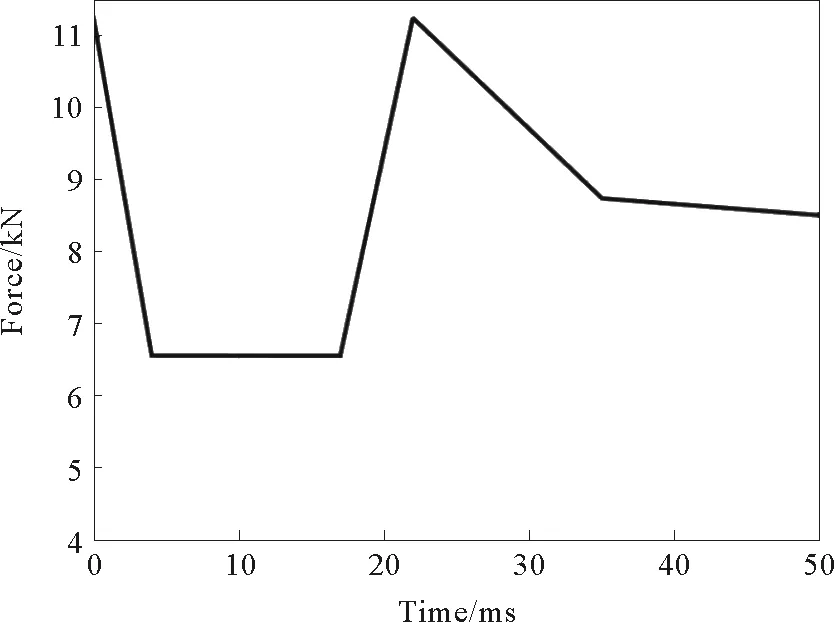
图6 悬臂端撞击力时程曲线Fig.6 Time history of impactforce loaded at tip
图7给出了空管道在承受端部撞击作用下不同时刻的变形曲线。对比实腹式截面悬臂梁,两者整体变形模式相似,均为梁段绕固定端发生大变形塑性转动[12]。然而对应图8示出的曲率分布曲线,仔细观察发现, 5.0 ms时刻,在距离撞击端部0.275 m的k1位置,其曲率已大于该管道的临界曲率κcr=1.25 m-1,表明此截面已因弯曲作用发生截面失效,在此处形成“结节”。随着响应深入,分别在k2、k3位置,即距离端部0.50、0.875m截面处,同样经历截面的局部失效产生的“结节”行为。在整体响应过程中,悬臂管段被k1、k2、k3位置处的“结节”分割为若干相对独立的管段。“结节”相邻的管段绕此转动,并消耗撞击能量。此响应过程涵盖了初始弹性、中期塑性强化和后期软化三个特点鲜明的阶段,其第三个阶段在实腹式截面悬臂梁中未曾出现。
图9~10分别给出了内充介质为水(内压15MPa)和细沙的管道在撞击载荷下的各时刻变形曲线。与文献[12]针对实腹式矩形截面梁的分析相同,整体管段在塑性动力响应过程中始终保持光滑连续,呈现前期弯曲塑性铰由端部至根部移动的“移行铰”阶段和后期根部“驻定铰”主导结构响应的鲜明特点。对比图7,两种情况均未出现空管道所表现的“结节”行为。

图7 空管道各时刻变形曲线Fig..7 Instantaneous deformed shapes of empty pipe

图8 空管道各时刻曲率分布曲线Fig..8 Instantaneous curvature distribution of pipe
对应图11~12示出的曲率分布曲线发现,除固定端外,两种工况的响应过程,尽管管段上某些截面分别接近其临界曲率3.2 和4.0m-1,但未发生超越现象。表明,管道除固定端截面外,其他截面均仅经历前期弹性,中期塑性强化过程,空管道工况下所出现的软化阶段没有出现。与空管道响应的差异表明,管道内充介质和压力通过在截面层次影响截面的弯曲行为,使得其塑性强化和软化行为间的临界曲率增大,进而影响结构的整体塑性动力响应行为。

图9 内充水和15 MPa压力管道各时刻变形曲线Fig.9 Instantaneous deformed shapes of pipe
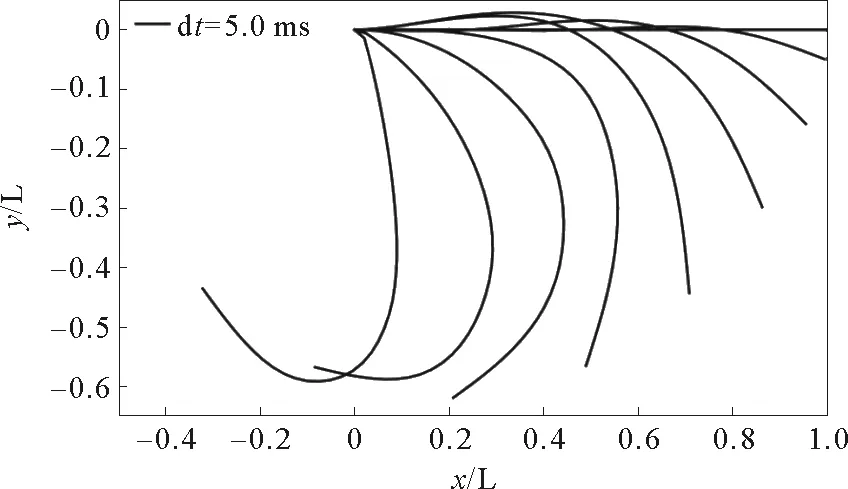
图10 内充细沙压力管道各时刻变形曲线Fig.10 Instantaneous deformed shapes of pipe

图11 内充水和15 MPa压力管道各时刻曲率分布曲线Fig.11 Instantaneous curvature distribution of pipe
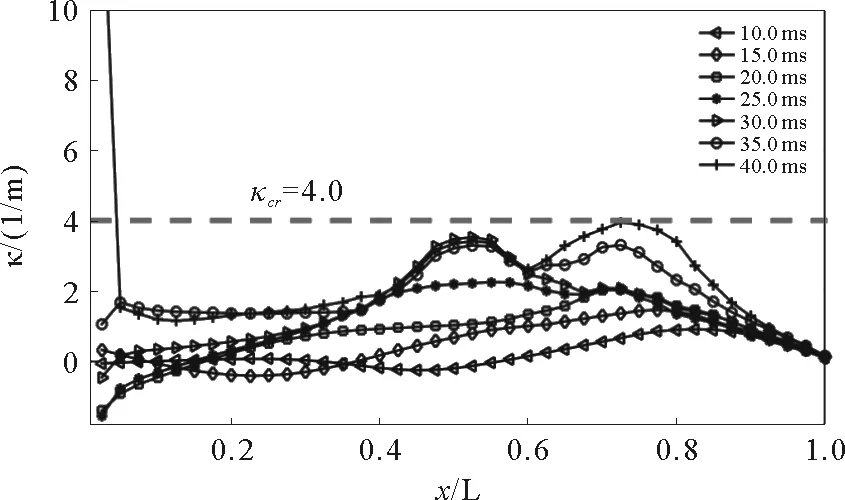
图12 内充细沙压力管道各时刻曲率分布曲线Fig.12 Instantaneous curvature distribution of pipe
3 结论
考虑管道内压和介质质量影响,采用实验测量的弯矩-曲率关系描述管道弯曲行为,基于变形后构型推导了管道大变形运动方程。数值计算表明,此控制方程可以准确模拟充压管道在撞击荷载作用下的动力响应过程。通过对比管道变形后形态以及曲率在管段长度方向的分布关系,考察了介质和充压水平对该类构件瞬态动力行为的影响。数值计算表明,薄壁空管道在弯矩作用下呈现明显的弹性-塑性强化-软化行为,在塑性动力响应中,会因管道某几个截面的失效,从而在的整体管段上形成“结节”。内充介质和压力可以有效抵制截面的局部扁平化和失效,从而提高截面“软化”的临界曲率,使得其弯曲行为向实腹式截面梁变形模式转移。
需要特别指出,所研究的悬臂管道因为支座边界条件原因,即使发生大变形,其动力响应过程中轴力始终维持较低水平。因此,为简化计算所采取的将弯矩和轴力解耦的做法是可行的。对于两端固支管道,响应过程中产生的数值较大的轴力会显著影响管段中弯矩的分布,并可能在响应后期主导结构的响应,相应控制方程不再适用。今后的研究应针对响应过程中弯矩-轴力的相互影响,推导即可准确描述管道局部变形,同时也可以把握管道整体响应行为的简单梁单元模型。
致谢:英国曼彻斯特大学李庆明博士(Dr.LI Qingming)曾在作者(刘锋)访学期间,对考虑内充压力介质下大变形动力控制方程的推导给予指导,在此致谢。
[1]张善元,路国运,程国强,等.圆管及内充压力介质管道撞击大变形与破坏[J].力学进展,2004,34(1):23-31. ZHANG Shanyuan,LU Guoyun,CHENG Guoqiang,et al.The advances on research of the impact damage and failure of empty and half-filled tubes[J].Advances in Mechanics,2004,34(1):23-31.
[2]JONES N,BRICH R S.Low-velocity impact of pressurized pipelines[J].International Journal of Impact Engineering.2010,37(2):207-219.
[3]YU T X,REID S R,WANG B.Hardening-Softening behavior of tubular cantilever beams[J].International Journal of Mechanical Science,1993,35(12) :1021-1033.
[4]REID S R,YU T X,YANG J L,et al.Dynamic elastic-plastic behavior of whipping pipes:Experiments and theoretical model[J].International Journal of Impact Engineering,1996,18(7):703-733.
[5]REID S R,WANG B,ALEYAASIN M.Structural modeling and testing of failed high energy pipe runs:2D and 3D pipe whip [J].International Journal of Pressure Vessels and Piping,2011,88(2):189-197.
[6]PRINJA N K,CHITKARA N R.Post collapse cross-sectional flattening of thick pipes in plastic bending[J].Nuclear Engineering Design,1984,83:113-121.
[7]PALMER A C,NEILSON A,SIVADASAN S.Impact resistance of pipelines and the loss-of-containment limit state[J].Journal of Pipeline Integrity,2003,2(4):231-240.
[8]NISHIDA M,TANAKA K.Experimental study of perforation and cracking of water filled aluminum tubes impacted by steel spheres [J].International Journal of Impact Engineering,2006,32(12):2000-2016.
[9]SHAH Q H,.Experimental and numerical study on the orthogonal and oblique impact on water filled pipes[J].International Journal of Impact Engineering,2011,38(4):330-338.
[10]LU G Y,ZHANG S Y,LEI J P,et al.Dynamic responses and damages of water-filled pre-pressurized metal tube impacted by mass[J].International Journal of Impact Engineering,2007,34(8) :1594-1601.
[11]刘锋,吴月磊,杨玉超,等.内充压力介质管道弯曲力学行为的实验研究[J].山东科技大学学报(自然科学版),2016,35(3):40-45. LIU Feng,WU Yuelei,YANG Yuchao,et al.Experimental study on the flexural behaviour of pipeline with internal medium and pressure[J].Journal of Shandong University of Science and Technology (Natural Science),2016,35(3):40-45.
[12]XI F,LIU F,LI Q M.Large deflection response of an elastic,perfectly plastic cantilever beam subjected to a step loading[J].International Journal of Impact Engineering,2012,48:33-45.
(责任编辑:吕海亮)
Transient Response of Pressurized Cantilever Pipe Subjected to Transverse Impact at Its Tip
LIU Feng1,2,WU Yuelei1,ZHANG Hang1,MENG Fanjian1
(1.Shandong Provincial Key Laboratory of Civil Engineering Disaster Prevention and Mitigation, Shandong University of Science and Technology,Qingdao,Shandong 266590,China; 2.State Key Laboratory for Disaster Reduction in Civil Engineering,Tongji University,Shanghai 200092,China)
In view of the problem of pipe whip,the present paper,taking the effects of internal medium and pressure into account,derived the large deformation governing equations based on the line element model after deformation.With the response characteristics of cantilever structure,uncoupled bending moment and axial force of constitutive equation taken into consideration,the bending behavior of cantilever pipe was described by adopting the experiment-based relationship of moment and curvature.The numerical simulation shows that this model can precisely simulate the mechanical process of elasticity,plastic hardening and softening in the initial,middle and late stage of pipe response respectively.Some “kinks” may occur at some position of the empty cantilever pipe due to the collapse of some sections under strong dynamic loading,showing up the “softening” behavior never occurring to solid-web sections.The internal medium and pressure can effectively impede the partial flattening of pipe section and improve its critical curvature,thus changing its plastic dynamic response behavior.
pressurized pipeline; medium; internal pressure; impact; plastic hardening-softening
2015-12-09
国家自然科学基金项目(51208289,11672165);土木工程防灾国家重点试验室开放基金项目(SLDRCE10-MB-04);山东省高等学校科技计划项目(J13LG05)
刘 锋(1977—),男,山东济南人,副教授,博士,主要从事结构减灾方面的研究.E-mail:feng.liu@sdust.edu.cn
O353
A
1672-3767(2017)03-0050-07
