磨片精磨区纤维轨迹模型的建立及磨齿作用频数的求解1)

花军 林晓亮 陈光伟

(东北林业大学，哈尔滨，150040)



磨片精磨区纤维轨迹模型的建立及磨齿作用频数的求解1)

花军 林晓亮 陈光伟

(东北林业大学，哈尔滨，150040)

通过对热磨机磨片精磨区内纤维运动的分析，阐述了纤维的流体特性；根据流体力学的运动学原理求解磨片精磨区间隙内纤维流体的运动轨迹模型，并建立纤维流体在精磨区内的轨迹方程；结合磨片的结构参数，运用轨迹方程推导磨齿作用频数的数学表达式，并通过计算实际磨片的磨齿作用频数和统计纤维的研磨质量数据探究二者之间的影响关系。结果表明：纤维流体在精磨区内的流动属于库特流动，并符合Naiver提出的线性滑移模型；其运动轨迹呈螺旋形，主要受磨片角速度、磨片间隙、磨片齿倾角的影响；磨齿作用频数受磨片结构参数影响，并与纤维的研磨质量具有相关性，合理的磨齿作用频数能够保证较高的纤维质量。

纤维分离；精磨；流体运动；轨迹模型；频数

热磨法是纤维板生产中纤维制备的重要方法，该法利用热磨机静、动磨片对纤维原料进行研磨，使纤维原料在研磨过程中发生解离。目前，国内外对于纤维解离的研究主要是从两个方面进行的。一方面是分析木材原料的形态、含水率和纤维质量、设备能耗之间的关系，这类研究主要以安德里茨等纤维分离设备制造企业为代表[1]；另一方面是建立磨齿对纤维作用的力学模型，通过模型分析和实验验证得到磨齿的齿形参数与纤维分离强度、能量消耗等的联系[2-3]。纤维在磨片内研磨时的运动速度和运动轨迹决定着纤维的研磨时间，研磨时间的长短影响着纤维受磨齿作用频数的高低，从而决定纤维质量的优劣，而目前对于纤维在磨片内部运动状态的研究较少。

在磨片的精磨区间隙内，从宏观来看，纤维的运动特征具有统计意义上的平均性和一致性，若只考虑纤维的整体运动性质而不考虑纤维单体的微观运动，则其总体行为模式与流体极其相似[4]。纤维的含水率较高，运动的纤维内部以及纤维与磨片之间存在的较大黏性切应力和较强的黏附性，这是黏性流体运动的特点和标志。大量的纤维在精磨区内处于强烈的挤压状态，纤维单体之间相互挤压和粘连，使整个纤维流体由连续介质组成，因此，纤维既具有流动性又具有连续性。笔者将运用流体运动学理论对纤维流体进行运动分析，并建立对运动轨迹模型。利用建立的数学模型推导出纤维流体流经精磨区时受磨片、磨齿作用频数的计算公式，通过分析几种磨片工作时磨齿作用频数与纤维质量的统计数据研究作用频数与纤维质量的关系。

1 纤维流体运动速度求解

1.1 纤维流体运动控制方程

研磨过程中磨片间隙设置为定值，纤维在间隙内的体积不会改变，视为不可压缩流体。基于前言对于纤维流体流动性和连续性的论述，根据黏性流体运动学理论，纤维流体的轨迹方程将由不可压缩流体流动连续性方程和黏性流体运动的微分方程导出[5]。

不可压缩流体流动连续性方程为

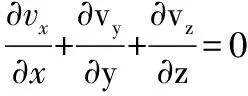
(1)

黏性流体运动的微分方程为

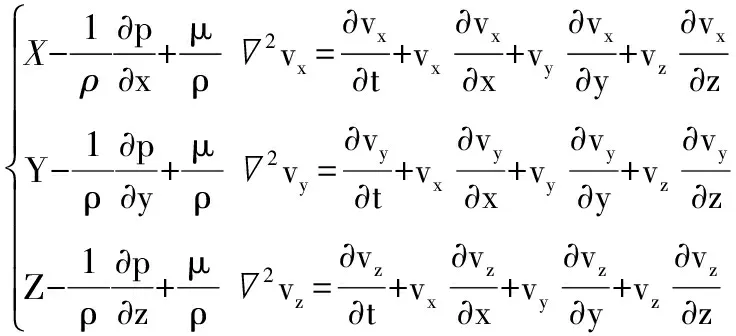
(2)

式中：X、Y、Z为外部作用于单位质量流体的体积力沿x、y、z方向的分量；为哈密尔顿算子，k。

1.2 磨片精磨区间隙内纤维运动速度分析

根据速度矢量叠加原理，将纤维进入磨片精磨区后的运动速度分解为绕z轴的周向运动和沿磨片磨齿的扩散运动，如图1所示。设精磨区内某纤维质点M的周向速度为u，扩散速度为w，二者的合成速度为v，M位置的极径值为r，M与磨片中心O的连线与x轴夹角为θ，磨齿的齿倾角为φ，磨片的精磨区内径大小为r0。

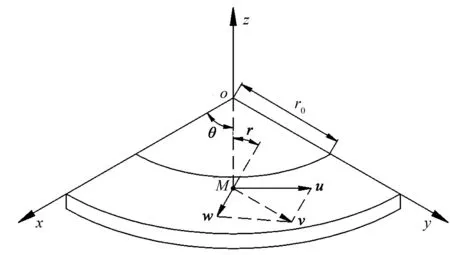
图1 纤维质点M的速度分解

1.2.1 纤维的周向运动

将磨片精磨区沿着圆周方向展开成直线，使动、静磨片转化成平行平板结构，采用流体平行平板间缝隙流动模型进行分析[6]。此时，纤维的周向运动转换成直线运动，如图2所示，若设纤维质点M周向运动的角速度为ω，则纤维质点M沿各坐标轴的速度为

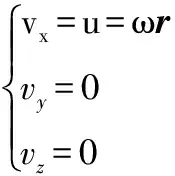
(3)

根据式(1)和式(3)，有∂vx/∂x=0，由于精磨区内纤维的体积力相比磨片对纤维的作用力来说很小，忽略体积力的影响。则式(2)可简化为

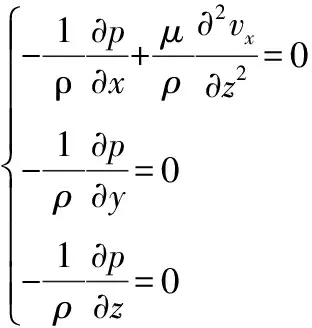
(4)

纤维周向运动的圆周轨迹上压强可认为处处相等，即∂p/∂x=0，得

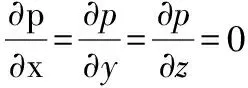
(5)

因此式(4)进一步简化为关于z轴坐标值的函数，即

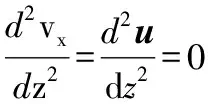
(6)

设动磨片转动的角速度为ω0，动、静磨片之间的间隙为hg，由边界条件

z=0,vz=0;

z=hg,vz=ω0r。

解得纤维质点M在磨片间隙内的周向速度为

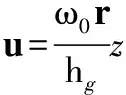
(7)

由式(7)看出，纤维在磨片间隙内作周向运动时，运动速度与动磨片角速度、磨片间隙及位置半径有关，因纤维自身的黏性还会沿间隙方向(z轴方向)产生速度梯度，即和动磨盘磨片接触的纤维层与磨片同步旋转，与静磨盘磨片接触的纤维层静止不动，两层之间的纤维运动速度呈线性分布，形成平行于磨片表面的剪切运动。该流动形式在流体运动学中称为库特流动[7]。其速度分布见图3。

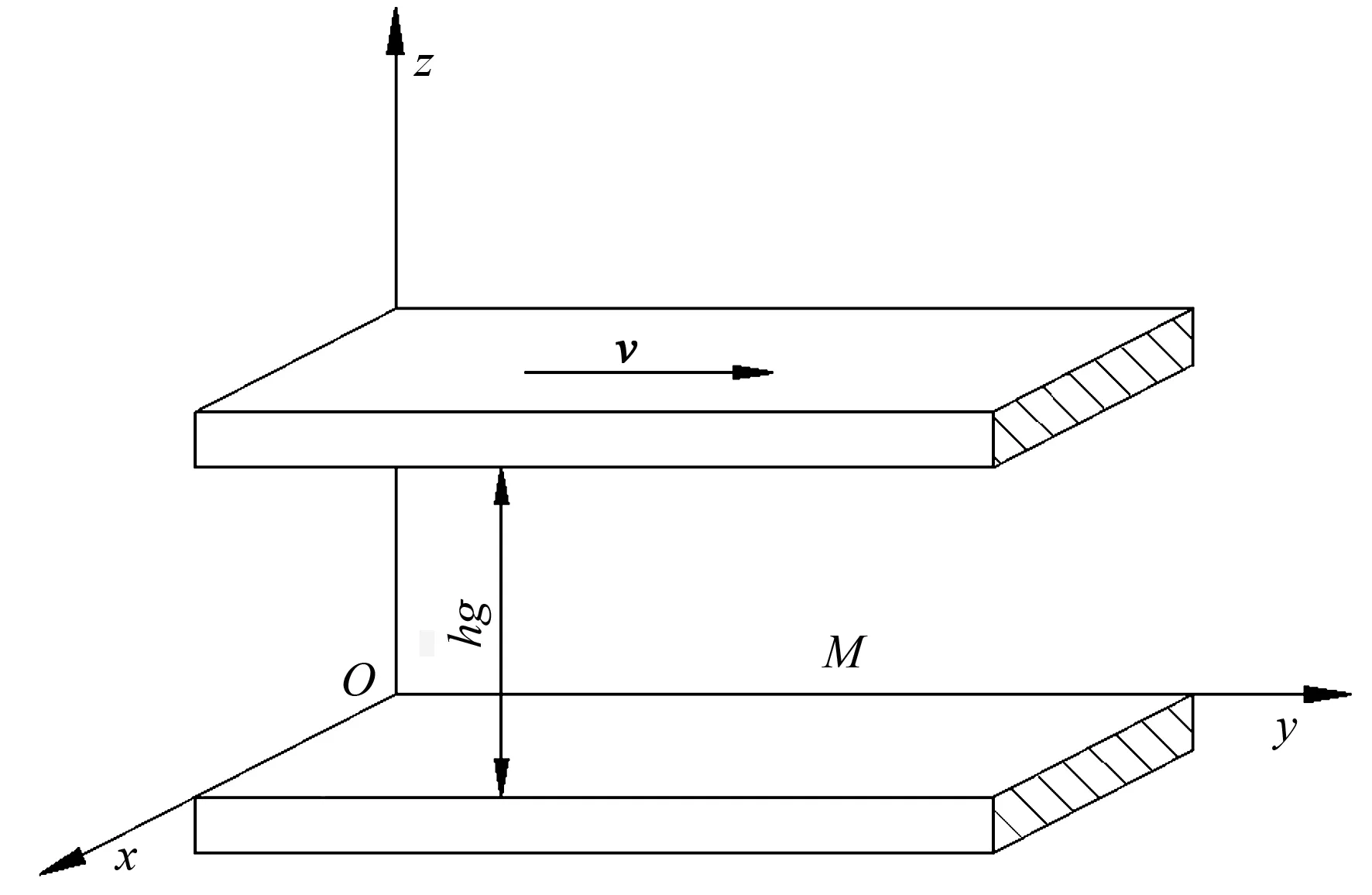
图2 流体平行平板间缝隙流动模型

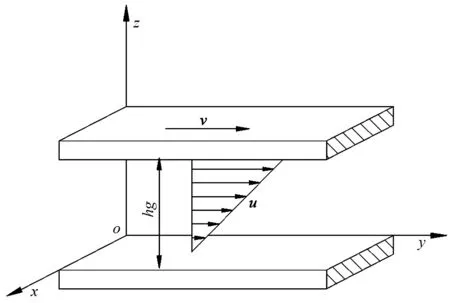
图3 纤维流体流动的速度分布

1.2.2 纤维的扩散运动

磨片精磨区间隙内的纤维遇到磨齿的作用时，受齿倾角的影响，纤维流体会沿磨齿的延伸方向向外扩散。由于周向速度与磨齿齿面的夹角为π/2+φ，则纤维的扩散速度w为

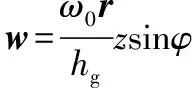
(8)

纤维的扩散速度表达式表明磨片精磨区间隙内纤维的扩散运动同样符合库特流动，其大小同样与动磨片角速度、磨片间隙及位置半径有关，并且受齿倾角的影响。由于扩散速度是极径值r的函数，而齿倾角又影响着纤维扩散路径的大小。因此齿倾角的设置决定着纤维在精磨区研磨时间的长短，合理的齿倾角能保证纤维良好的研磨质量。

1.2.3 纤维的运动速度及其修正

由速度合成定理，利用纤维的扩散速度和周向速度表达式对合成速度的大小进行解算。根据余弦定理得

(9)

解得纤维的合成速度为

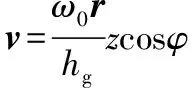
(10)

从式(10)中可以看出，纤维在磨片精磨区间隙内的速度受磨片间隙、磨片角速度及磨齿倾角的影响。这些参数共同影响了纤维的研磨时间，纤维制备工艺中通过调整各参数的大小，可以控制纤维分离的质量。

对纤维周向速度、扩散速度和合成速度表达式的导出都是建立在磨片表面为水力光滑壁的条件之上的；但是，由于磨片内表面并不光滑且存在磨齿，纤维在磨片间隙内的流动将受到很大阻力，顶层纤维的运动无法与动磨片同步运动，而呈现出速度滞后。另一方面，由于动、静磨片之间的间隙很小，动磨片的旋转对静磨片表层纤维的拖拽作用不可忽略，即底层纤维运动速度不为零。

基于以上两个方面的分析，可以得出与静磨片接触的纤维在解离过程中将会产生线性滑移。这种滑移又会减小z轴方向纤维运动的速度梯度，与Naiver提出的线性滑移模型相符[8-9]，滑移速度的大小与hg成反比，如图4所示。

在此对式(7)、(8)和(10)得出得速度表达式引入参数Bv和d进行修正。其中：Bv为考虑磨齿阻力的修正系数；d为静磨片表面到速度为零的虚拟点O′的距离，是考虑到磨片表面粗糙程度的修正系数。修正后的速度表达式为

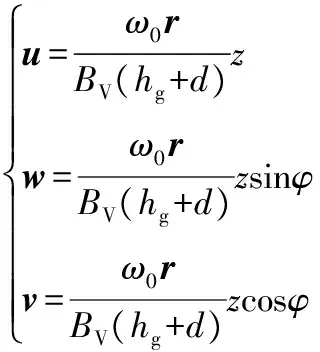
(11)

由式(11)可知，磨片精磨区间隙内的纤维运动速度符合库特流动模型，速度大小受磨片角速度、磨片间隙、磨齿倾角和磨片表面粗糙程度及磨齿阻力的控制，通过影响纤维的研磨时间，进而影响纤维的分离质量和热磨机的能耗[10]。

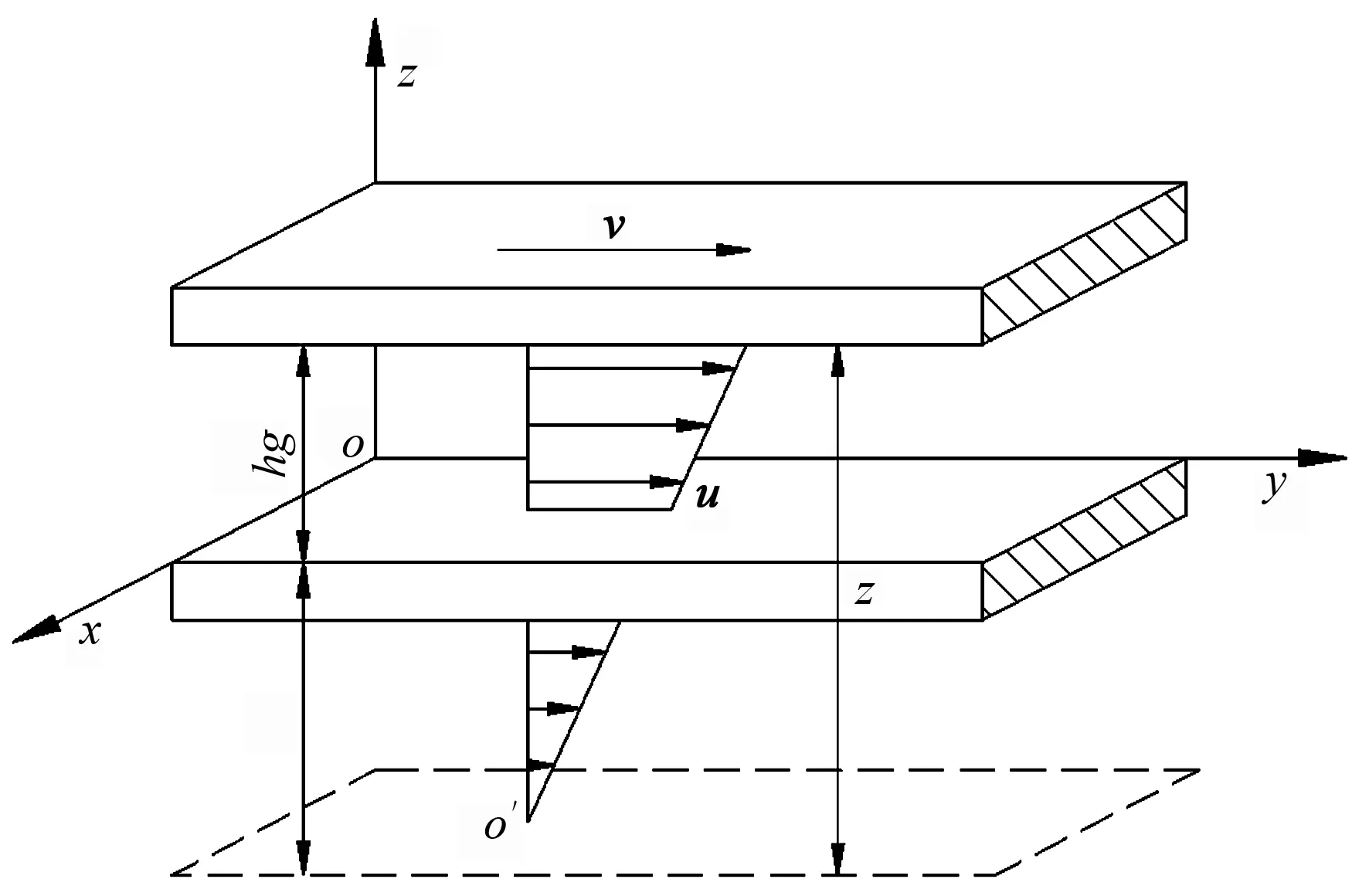
图4 纤维流体的线性滑移

2 纤维流体运动轨迹方程的建立

2.1 轨迹方程的建立

如图5所示，在极坐标下，假设纤维质点M在t时刻到达M1，极径值为r，经过时间dt后，以速度v到达点M2处，极径值为r+dr，对应的转角为dθ，则

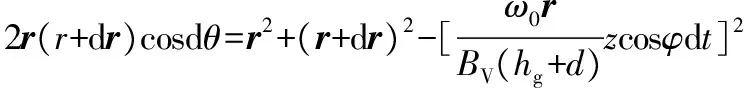
(12)

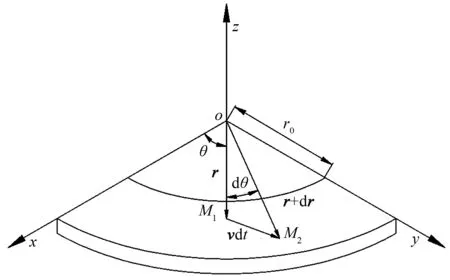
图5 纤维在磨片间隙内的运动

当dθ趋于零时，cosdθ趋于1，则式(12)简化为

(13)

解微分方程(13)得

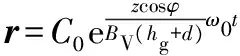
(14)

当t=0时，r=r0，即C0=r0代入(14)得

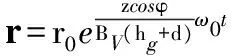
(15)

式(15)即为磨片精磨区间隙内纤维运动轨迹的数学模型。从轨迹方程的表达式可以看出纤维流体运动的轨迹为螺旋线，其轨迹形状受磨片转速、磨片间隙和磨齿结构及表面粗糙度影响。

2.2 修正系数的估算

式(15)中的修正系数BV和d在实际生产中难以测定，但可以通过生产设备年产量和热磨机及磨片的相关参数进行估算。

设热磨机的年产量为Va，则纤维的每秒产出率可算，设为Vs。对于动、静磨片磨齿与齿槽进行体积补偿运算，设磨片外径为R0，齿高为hc，则磨片间纤维流体的出口面积为

S=2πR0(hg+hc)。

(16)

设纤维流体垂直于磨片方向的出口速度为vs，则有

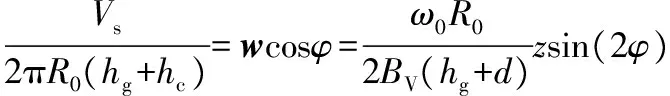
(17)

此时应取z=hg/2，则将BV和d的估算转换为对BV(hg+d)的计算，估算式为

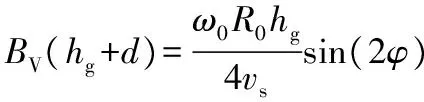
(18)

现以某国产磨片(内径1 080 mm，外径1 372 mm)的相关参数为例，取磨片精磨区间隙内z=hg/2的纤维流体层，利用Matlab绘制出磨片间隙内某纤维质点的运动轨迹如图6所示。

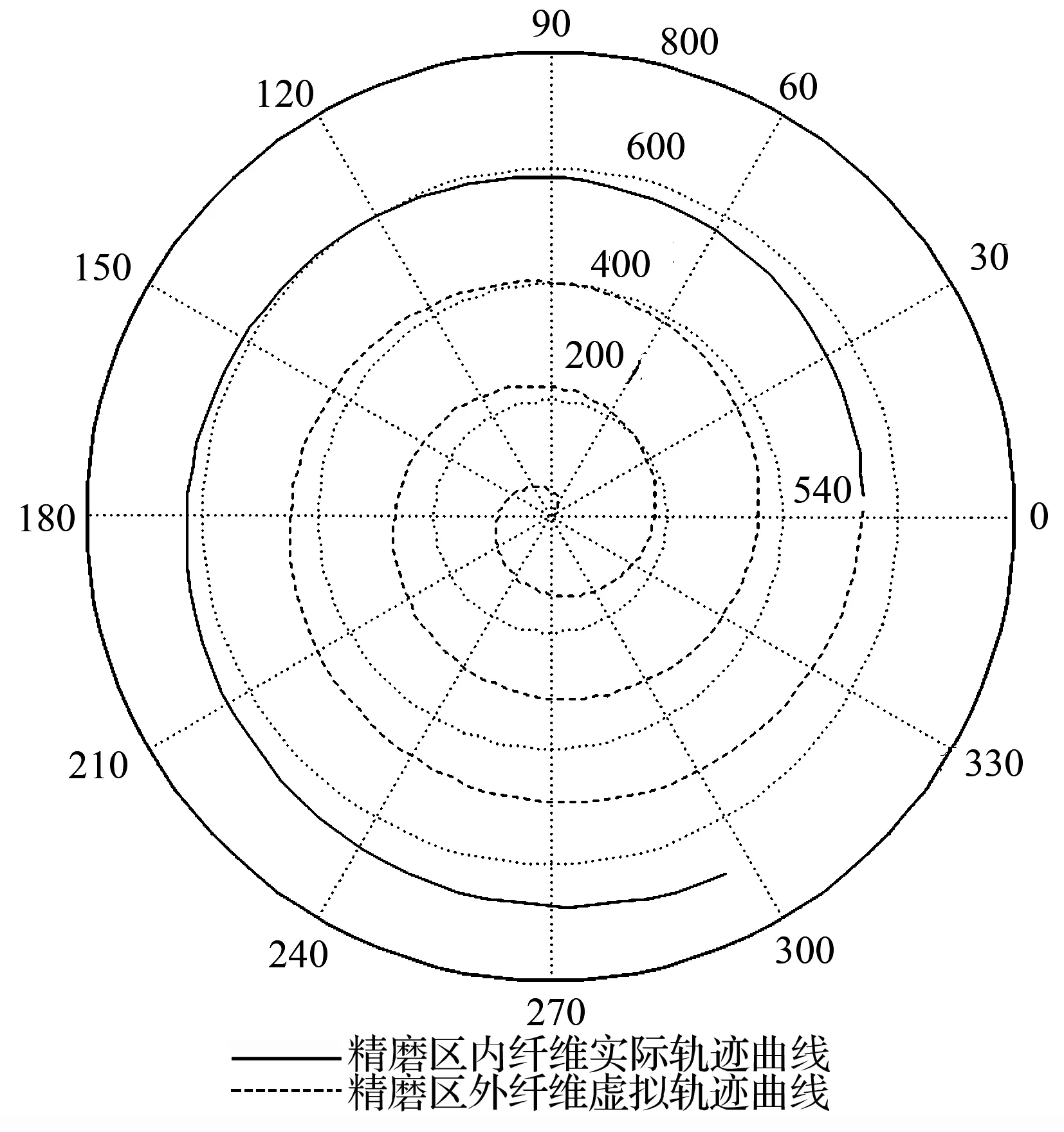
图6 纤维在磨片精磨区间隙内的运动轨迹

通过模型及图像可以看出，精磨区纤维在x-y平面上运动的轨迹呈螺旋形。当z值改变，则不同纤维流体层的运动轨迹线发生相应变化。通过几何求解得到纤维的扩散路程sw为

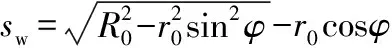
当磨片规格和齿倾角一定时，sw为定值。由式(8)知，当z值减小时，相同r值时的扩散速度小，因此研磨时间长。由于ω0为定值，则轨迹线的圈数就多。

3 磨片磨齿作用频数与纤维质量的关系

热磨机在纤维分离过程中，磨片解离纤维的质量和纤维流体的流动状态之间具有密切的关系。纤维分离是纤维原料逐次流经磨片磨齿表面时，因磨齿形成的压缩、剪切和摩擦等多种作用力综合作用后，造成原料被反复压溃、切断和分丝的结果。纤维质点M在沿着运动轨迹流动的过程中，由于动磨片的高速旋转，M受到磨齿一定频数的作用。若频数适当，则纤维分离的质量就好，纤维流体的运动和所受磨齿作用的频数与磨片齿形结构密切相关；若磨片的齿形结构不合理，原料在磨片内的受力频数或高或低，都会造成纤维分离质量的下降，即纤维可能被过度研磨或研磨的不充分。因此，了解磨齿对纤维流体作用频数与纤维研磨质量的关系尤为重要。以下对磨齿作用频数与纤维质量关系进行理论推导和实验研究。

由纤维质点M的轨迹方程(15)，取r=R0可以计算z坐标处纤维质点M流经精磨区到达出口所用的时间为

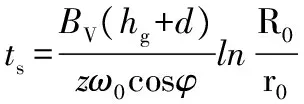
(19)

设纤维质点M流经精磨区所受磨齿作用的频次为k，磨齿齿数为m，磨片转速为n，则

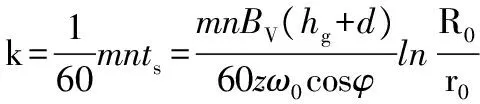
(20)

将式(18)带入式(20)得

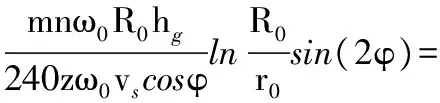
(21)

式(21)即为磨片磨齿作用频数k的数学表达式。可以看出，频数的大小与磨片转速和磨片的规格、齿数、齿倾角及磨片间隙等参数有关，vs由式(17)计算。磨片尺寸和间隙的增大、磨齿齿数的增多以及齿倾角的加大都会使磨片磨齿作用频数增加，从而加强对纤维的研磨作用。磨片间隙内不同z值处的纤维研磨强度不同，在磨片规格、齿倾角一定时，由式(8)可知，z值越大，纤维在精磨区内的扩散速度越大，即被磨片研磨的时间短，经历的磨齿作用频数越小，这与式(21)的表达相一致。实际生产中应当综合考虑磨片结构的各个参数，使纤维得到适当的作用频数，从而防止研磨过度或不充分。

现以我国某几家纤维板生产企业的几种磨片为例，对其研磨出的纤维采用OLYMPUSBX51型生物显微镜进行测量和统计，利用统计结果和相应的磨片参数探究磨片磨齿作用频数与纤维质量的关系。所用磨片配备的热磨机电机转速均为1 500r/min，外径1 372mm和1 060mm的磨片的分别以年产量15万m3和10万m3对vs的估算[11]。频数的z轴坐标值统一取为平均间隙高度。根据《木材工业手册》，以早材落叶松的纤维长度、长径比与大青杨、山杨和小叶杨的平均纤维长度、平均长径比分别作为合格纤维样本尺寸形态的上下限参考值，即合格纤维长度为1.27～3.51mm，长径比为47.0～60.5[12]。对每种纤维的长度合格率和长径比合格率进行统计计算，磨片的结构参数及纤维质量统计的百分比见表1。

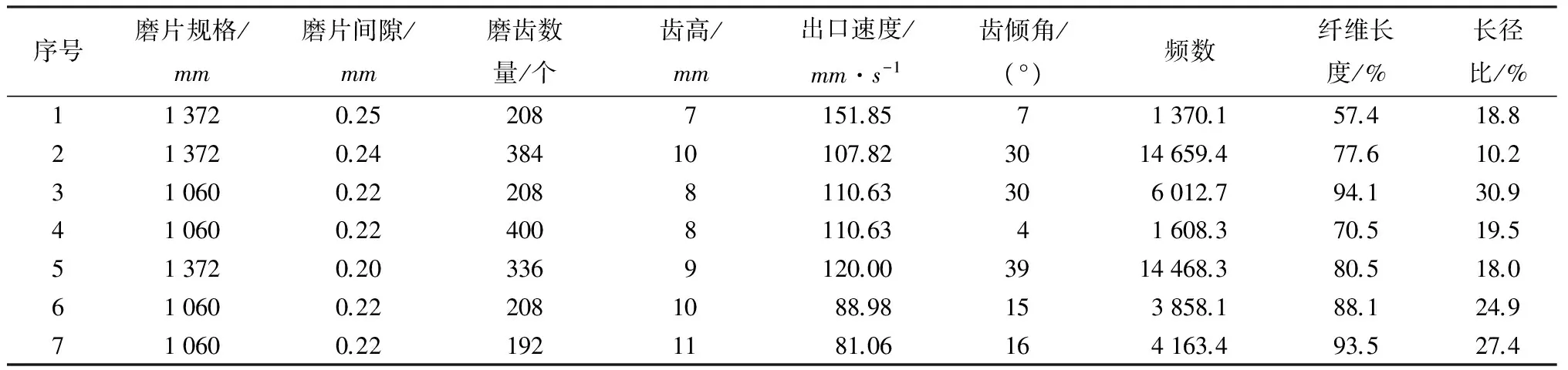
表1 磨片结构参数及纤维测量统计结果

以频数为横坐标，纤维长度的合格率和长径比合格率作为纵坐标绘制曲线图(见图7)。可以看出，磨片磨齿作用频数对于纤维长度合格率的影响呈现由低到高再到低的变化趋势，而对于长径比合格率的影响基本与纤维长度影响趋势一致。磨片磨齿作用频数较低使纤维研磨得不够充分，频数较高又会研磨过度，这都会使纤维的合格率降低。因此，选择合理的磨片结构参数能有效提高纤维的研磨质量。

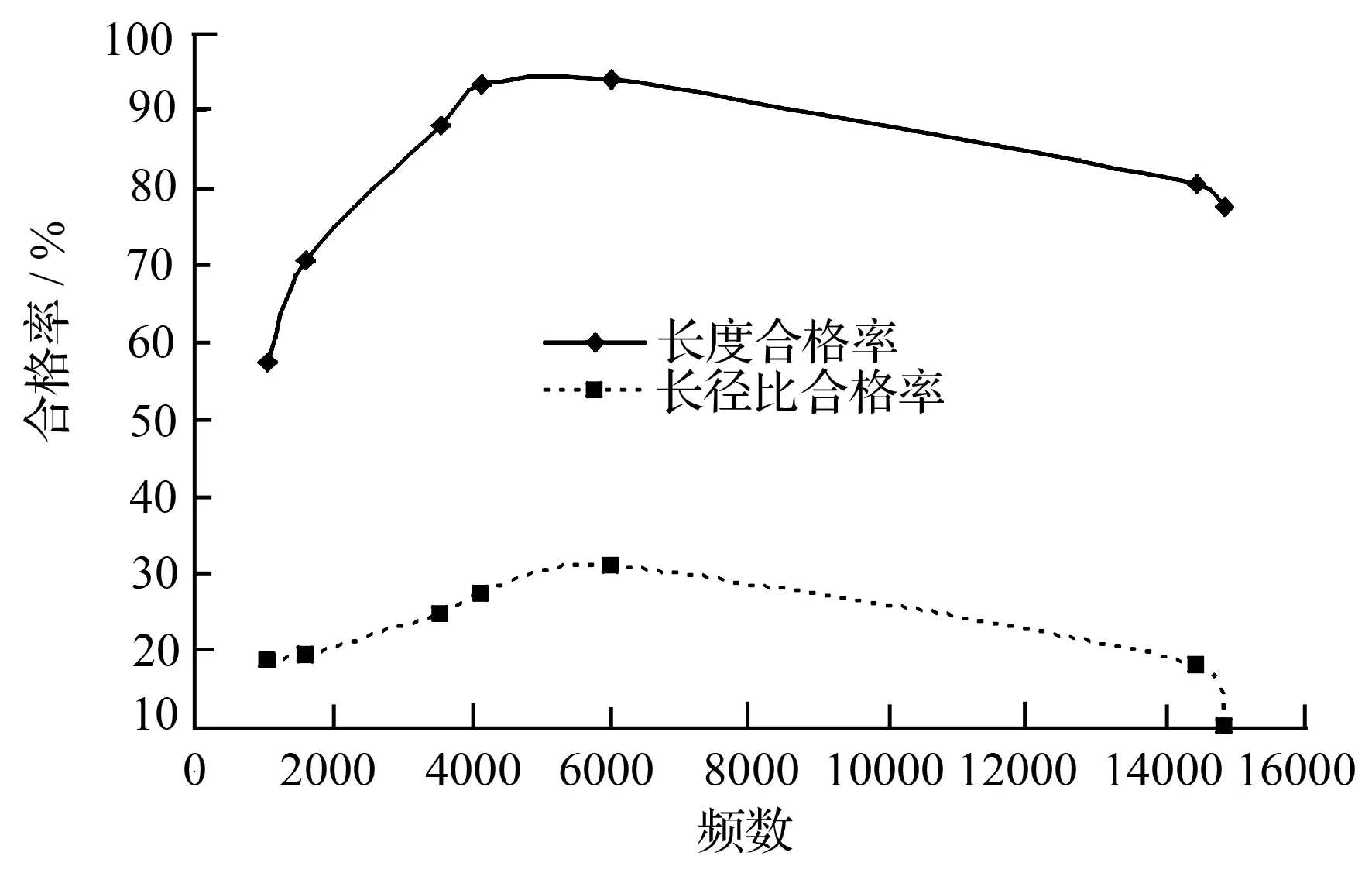
图7 纤维长度合格率和长径比合格率与磨片磨齿作用频数的关系曲线

4 结论

磨片精磨区间隙内纤维流体的周向运动、扩散运动以及合成速度均为库特流动，速度大小沿着z轴线性分布形成分层剪切，速度大小受磨片角速度、间隙大小及齿倾角的影响；因磨片间隙尺寸较小，又受齿形及磨片表面粗糙程度的影响，纤维流体的运动符合Naiver提出的线性滑移模型。

纤维运动的轨迹呈螺旋形，磨片角速度、间隙及磨齿齿倾角影响磨片间隙内运动轨迹的形状，不同纤维流体层内的轨迹线形也不同。z轴坐标值较小的纤维流体层内，相同极径值的纤维扩散速度小，分离的时间长，螺旋轨迹的圈数也就多。

磨片磨齿作用频率与磨片的规格、间隙、转速和磨齿的齿数、齿倾角等参数有关，具有大尺寸、高转速、多齿数和较大齿倾角的磨片对纤维的作用频数较高。z轴坐标值相同的纤维在较大间隙内由于扩散速度较慢，所受磨齿作用时间长，作用频数高。纤维分离质量和受磨片磨齿的作用频数具有相关性，作用频数较小，纤维研磨不充分，作用频数较大，纤维研磨过度，都会降低纤维的合格率。

由此可见，研究纤维流体在磨片间隙内的运动轨迹及磨齿作用频数与纤维研磨质量的影响关系对获得较高合格率的纤维制品具有重要意义。实际生产中选择合理的磨片结构参数能够保证较高的纤维研磨质量。

[1] 沈毅，方普新.热磨机20年发展的回顾[J].中国人造板，2011(3)：130-133.

[2] 董继先，职艳芳.Z形磨齿新型高浓盘磨机磨片[J].中国造纸，2008，27(11)：49-50.

[3]BERGJE，GULLIKSSONME,GRADINPA.Ontheenergyconsumptionforcrackdevelopmentinfiberwallindiscrefining-amicromechanicalapproach[J].Holzforschung，2009，63(2):204-210.

[4]SEDIGHIGILANIMS,NAVIP.Experimentalobservationsandmicromechanicalmodelingofsuccessivedamagingphenomenoninwoodcells’tensilebehavior[J].WoodScienceTechnology，2007，41 (1):69-85.

[5] 林建忠，阮晓东，陈邦国，等.流体力学[M].北京：清华大学出版社，2005：2-314.

[6]SENGERJJ,OUELLERD.Factorsaffectingtheshearforcesinhighconsistencyrefining[J].JournalofPulpandPaperScience，2002，28(11):364-369.

[7]JAMALMS.Fluidflowhandbook[M].London:McGraw-HillEducation，2002:4-45.

[8] 吴承伟，马国军，周平.流体流动的边界滑移问题研究进展[J].力学进展，2008，36 (3) ：265-266.

[9] 吴承伟，马国军.关于流体流动的边界滑移[J].中国科学G辑:物理学、力学、天文学，2004，34(6)：681-690.

[10] 牛治军,王宝金,俞敏.热磨机的研究现状与发展趋势[J].林业机械与木工装备，2012(12)：8-12.

[11] 农林水产局林业实验场编.木材工业手册[M].北京：中国林业出版，1991：194-195.

Establishment of Tajectory Model for Fiber in Fine Grinding Zone of Disc and Solution of the Frequency of Gear Grinding Effect//

Hua Jun, Lin Xiaoliang, Chen Guangwei(Northeast Forestry University, Harbin 150040, P. R. China)//

Journal of Northeast Forestry University，2017,45(4)：94-98.

Movement of fiber in fine grinding zone of refiner disc was analyzed and fluid properties of fiber were elaborated. Trajectory model of fiber fluid was solved by kinematics of fluid mechanics through which equation of trajectory in fine grinding zone was established. The formula of the frequency of gear grinding effect in combination with parameter of disc structure was solved through the equation of trajectory. Through calculating the frequency of gear grinding effect of real disc and compiling the statistics of the fiber quality the relationship was analyzed between them. The flow of fiber fluid is Coutte flow and accords with Linear slip model proposed by Naiver. The trajectory is helical and mainly influenced by disc speed, clearance and tooth Inclination. The frequency of gear grinding effect is influenced by parameter of disc structure, and it has a relationship with the properties of fiber. Therefore, reasonable frequency can ensure high quality of fiber.

Separating fiber; Fine grinding; Fluid movement; Trajectory model; Frequency

花军，男，1959年5月生，东北林业大学机电工程学院，教授。E-mail：huajun81@163.com。

2016年10月7日。

TS642

1)教育部高等学校博士学科点专项科研基金(博导类)课题(20130062110005)。

责任编辑：戴芳天。