地震荷载作用下钢筋混凝土柱的滑移变形
2017-06-01朱绩超王响赵丽华
朱绩超,王响,赵丽华
(1.大连交通大学 土木与安全工程学院,辽宁 大连 116028; 2.大连理工大学 建设工程学部,辽宁 大连 116024; 3.美国加州大学 圣地亚哥分校 结构工程系,美国 加州 拉贺亚市 92093- 0085)*
地震荷载作用下钢筋混凝土柱的滑移变形
朱绩超1,2,王响3,赵丽华1
(1.大连交通大学 土木与安全工程学院,辽宁 大连 116028; 2.大连理工大学 建设工程学部,辽宁 大连 116024; 3.美国加州大学 圣地亚哥分校 结构工程系,美国 加州 拉贺亚市 92093- 0085)*
根据钢筋滑移的受力变形原理和Alsiwat-Saatcioglu模型假定推导出钢筋的显式表达式;基于转动弹簧模型和滑移截面模型,阐述了由滑移量-应力关系确定柱端弯矩-转角和构件的荷载-滑移变形关系的理论方法;开发了该方法相应的计算程序对上述两种模型的适用性进行了评定,结果表明采用滑移截面模型得到的钢筋混凝土柱构件荷载-滑移变形反应比转动弹簧模型更为准确.
钢筋混凝土柱;滑移变形;转动弹簧模型;滑移截面模型
0 引言
地震荷载作用下的钢筋混凝土柱的侧向变形通常包括弯曲变形、剪切变形和粘结-滑移变形.在弯矩作用下,柱端部截面的纵向钢筋受到向外的拔出力,沿其锚固区(梁柱节点或基础)内发生滑移,钢筋在锚固长度上相对其周围混凝土产生的滑动,即为钢筋的相对滑移.钢筋的相对滑移导致柱端产生附加刚体转动,柱构件产生了粘结-滑移变形,这种附加转动对构件侧向变形能力和刚度有显著影响.Alsiwat[1]通过试验研究指出在分析时忽略钢筋相对滑移效应将使得侧向变形的计算结果偏小.Sezen[2- 3]亦由试验结果得出钢筋相对滑移将对构件侧向变形的贡献较大,特别是当轴压比较低时,钢筋滑移引起的构件侧向变形约占钢筋混凝土柱屈服时总侧向变形的30%~40%.马颖[4]、张勤[5]通过试验研究及统计分析,认为钢筋滑移变形约占住总侧向变形的1/3.综上所述,如果在钢筋混凝土柱的受力分析中忽略了钢筋粘结-滑移变形,通常容易低估结构的总体变形,引发安全隐患.因此,本文将对钢筋滑移变形的分析方法进行论述,基于理论研究通过锚固钢筋滑移量与应力的关系确定柱构件的荷载-滑移变形关系的有效方法.
1 钢筋相对滑移量模型
锚固钢筋的实际受力变形原理十分复杂,混凝土强度等级、柱截面几何尺寸、保护层厚度、箍筋约束效应、纵筋布置方式等因素均将影响钢筋的粘结-滑移行为.即使相同的试验条件,得到的试件数据也存在一定的离散性.微观模型中的局部粘结应力与相对滑移之间的函数关系通常由钢筋拔出试验得到,其中Eligehausen[6]提出的局部粘结应力-钢筋滑移本构模型与试验数据吻合较好,在研究中应用广泛.由于采用该模型建立的钢筋和混凝土界面力学行为与实际情况更接近,故其计算结果与试验结果吻合性也更好;但是计算精度的提高在很大程度上是建立在细分单元的基础上,故其计算效率并不高,不适用于构件或结构的整体分析.
为了能更好的适应于构件或结构的整体分析,并能准确的分析锚固钢筋的粘结-滑移行为, Alsiwat-Saatcioglu[1]提出了钢筋应变在锚固长度ld上分段线性分布的假设.根据锚固段钢筋受力-变形特点的差异将其分为四段,分别为弹性段(长度为le)、屈服平台段(长度为lyp)、应变强化段(长度为lsh)和锥形拔出段(长度为lpc),钢筋滑移模型如图1所示.钢筋应力和应变在锚固长度上的分布见图1(a)和(b)所示.该模型假定弹性段均布粘结应力τe;屈服平台段和应变强化段上粘结应力由均布粘结应力τe和摩擦作用引起的附加均布粘结应力τf叠加而成;锥形拔出段上无粘结应力,其分布模式见图1(c).研究同时表明,钢筋混凝土节点由于有箍筋约束往往不会发生锥形拔出破坏现象,故本文不考虑锥形拔出段对钢筋滑移量的影响.
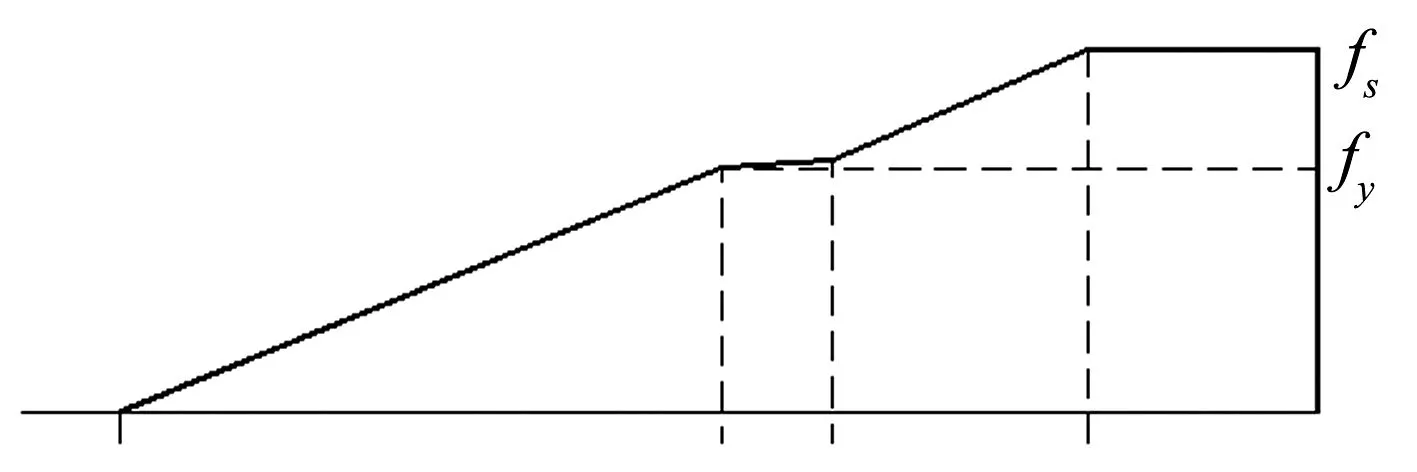
(a)锚固长度上钢筋的应力分布
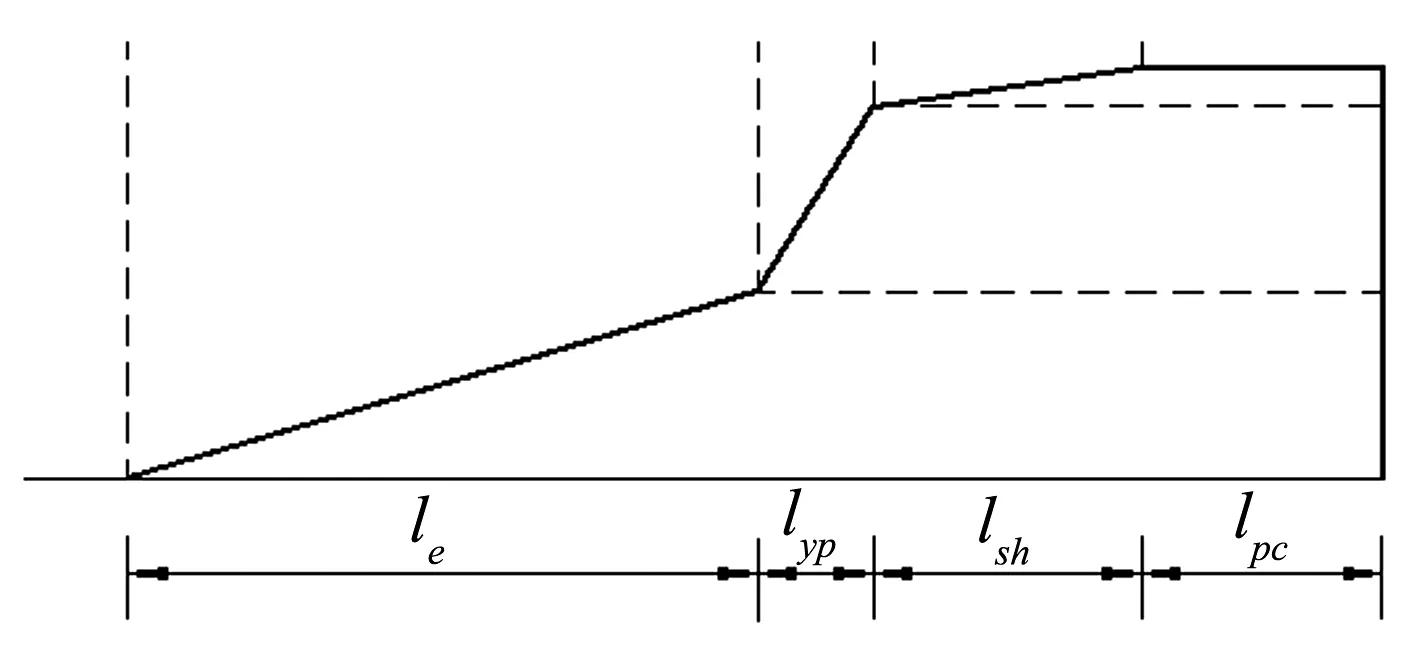
(b)锚固长度上钢筋应变分布
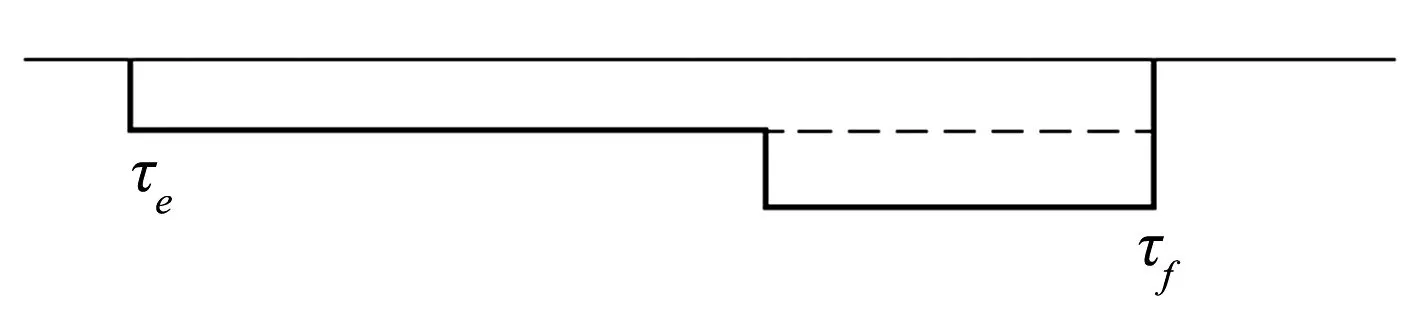
(c)锚固长度上粘结应力分布
当钢筋应力小于屈服强度时,为弹性段;当钢筋应力超过屈服强度后钢筋将进入屈服阶段及应变强化阶段,对应屈服平台段和应变强化段,钢筋滑移量急剧增大.各区段的长度为:
弹性段
(1)
屈服段
(2)
应变强化段:
(3)
其中,fs为锚固钢筋的端部应力;fy为钢筋屈服强度,单位MPa;fsh为钢筋应变强化起点处应力;db为受拉钢筋直径,单位mm.
弹性段均布粘结应力τe可按下式计算:
(4)
假定钢筋和混凝土界面上的粘结应力τe沿锚固长度ld均匀分布,根据钢筋自由体受力平衡条件可得,可得钢筋锚固长度ld,单位mm:
(5)
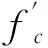
而由摩擦作用引起的附加粘结应力τf则按以下公式计算:
(6)
其中,SL和SH分别为锚固钢筋的肋间距和肋高.
由钢筋受力变形的线弹性假设又可知钢筋应变沿锚固长度亦呈线性分布,钢筋应变在锚固长度上的分布如图1(a)所示.钢筋加载端相对周围混凝土的滑移量s则可以通过对锚固长度段的钢筋应变进行积分得到,如弹性段le(εs≤εy)钢筋应力和滑移量之间的函数关系,具体表达式为:
(7)
其他各段的滑移量s亦可采用该方式进行计算,限于篇幅不再赘述.
2 由钢筋滑移引起的构件变形
钢筋混凝土柱端锚固钢筋由于滑移导致柱端截面产生附加转动,而这种转动将使构件产生侧向滑移变形.在钢筋混凝土柱构件的受力-变形分析中如忽略该侧向变形将低估构件的变形能力、而高估构件刚度以及耗能能力.文献[7]建议采用刚度折减的方法考虑粘结-滑移效应,但折减系数的取值缺乏理论根据,且无法反应往复加载作用下构件的受力-变形行为,因此该方法局限性较大.而另一种常用方法是在钢筋混凝土构件端截面处设置塑性铰考虑粘结-滑移效应[8].该方法力学概念清楚,能有效的考虑由钢筋滑移引起的构件转动及侧向变形,本文将采用设置塑性铰的方法分析钢筋滑移引起的柱构件变形.
采用该方法首先需要建立钢筋滑移量s和附加转角θs的关系,定义截面转动中心而得到钢筋相对滑移引起的附加转角θs:
(8)
其中,d为受拉钢筋至截面受压区边缘的距离;c为截面的转动中心至截面受压区边缘的距离.由于转动中心位置受多种因素影响,准确判断其位置十分困难,故在计算中通常假定柱端截面中和轴位置即为钢筋滑移的转动中心,如图2所示.
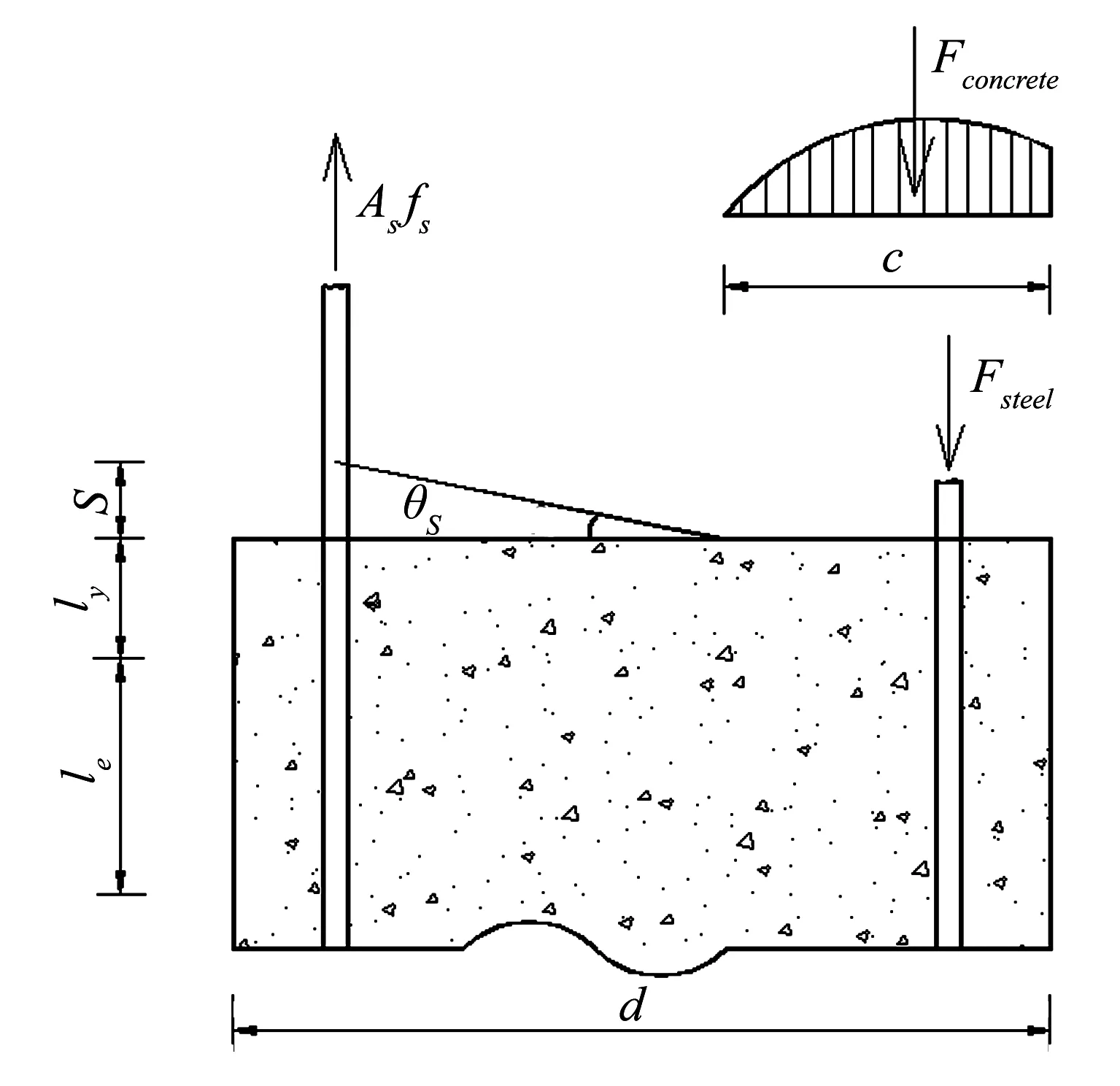
图2 钢筋滑移引起的附加转角
此时,由钢筋滑移引起的柱构件侧向变形Δs为:
(9)
其中,θs为钢筋滑移产生的附加转动;L为钢筋混凝土柱构件固定端至反弯点的长度,对于双曲柱L为试件长度的一半,对于悬臂柱L为试件长度.
3 粘结-滑移模型
本文列举了两种常见的粘结-模型,分别为转动弹簧模型和滑移截面模型.
3.1 转动弹簧模型
非线性转动弹簧的弯矩-转角关系是在柱构件的实际受力变形分析的基础上得到的,Alsiwat和Saatcioglu[1]给出了由锚固钢筋滑移量得到截面弯矩-转角的单调加载曲线的有效方法.文献[1]建议基于柱端截面的弯矩-曲率分析结果,确定截面弯矩与锚固钢筋应力应变以及截面中和轴位置的对应关系;根据式(7)计算出钢筋相对滑移量;通过式(8)得到柱端截面的附加转角,明确单调荷载作用下柱端截面处的弯矩-转角关系曲线.将得到的弯矩-转角曲线简化为分段折线模型,即单调荷载作用下的非线性转动弹簧的本构关系模型.
使用该方法分析锚固钢筋屈服前柱构件的滑移变形行为能得到比较准确的分析结果;但是由于在计算时假定转动中心位于截面中和轴位置,当受拉钢筋屈服后,截面受压区高度迅速减小而导致转动半径的增大,这样就低估了钢筋滑移引起的转动变形,高估了屈服后的构件刚度,造成一定的安全隐患.此外,在截面分析时通常对柱构件施加恒定轴力,所以转动弹簧预先设定的弯矩-转角关系无法反应往复荷载作用下柱构件轴力变化的影响,从而导致分析结果的误差.
3.2 滑移截面模型
Zhao和Sritharan[7]提出了在梁柱单元与节点相连接的截面处设置纤维截面的方法考虑由钢筋滑移引起的柱构件附加转动效应.滑移截面应与相邻梁柱单元截面保持相同的截面几何尺寸和纤维划分模式,但由于滑移截面无实际长度,故其纤维应反映材料的应力-位移关系.图3为钢筋滑移截面示意图,图中给出其与梁柱单元的纤维截面不同点.
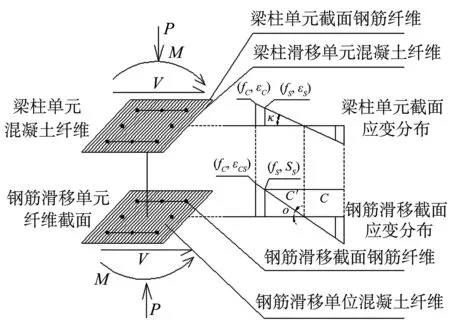
图3 滑移纤维截面示意图
滑移截面上钢筋纤维的材料本构关系应为钢筋滑移量-应力关系.Zhao和Sritharan[8]根据大量锚固钢筋拔出试验结果提出了钢筋滑移量-应力模型.
这里需要指出,钢筋滑移截面上混凝土可以与梁柱单元截面混凝土选取相同的本构模型,但由于滑移截面上的纤维需反应材料的应力-位移关系,因此必须对混凝土原来的应力-应变关系进行调整,调整原则为钢筋屈服前钢筋滑移截面与相邻梁柱单元截面中和轴位置保持基本一致,必须使得两截面上钢筋和混凝土的本构关系分别保持相应的比例.
4 算例分析
本文将采用文献[9]提供的试件1和2的荷载-滑移变形试验数据对比上述两种计算模型.两个试件几何尺寸、材料属性和配筋完全相同,但施加的竖向荷载有明显差异.试件的几何尺寸和材料参数如表1所示.
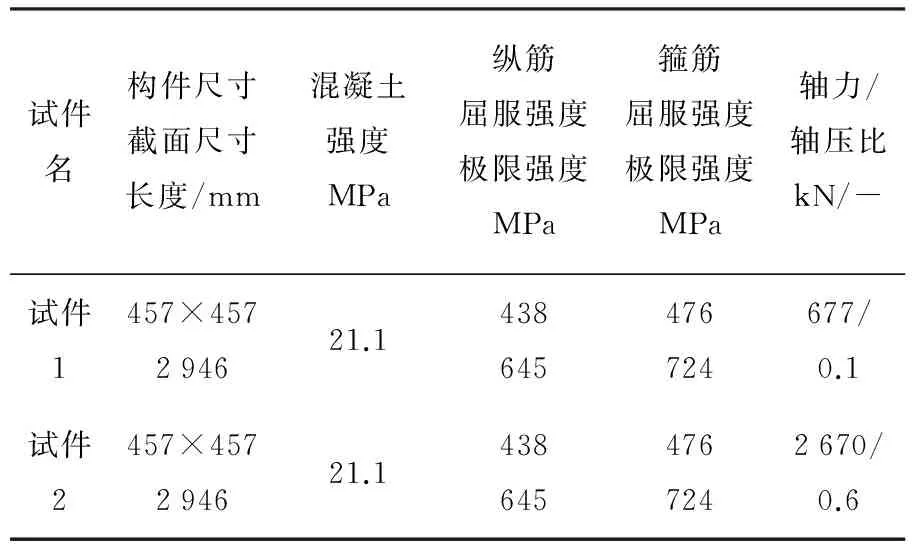
表1 试件尺寸与材料参数
本文分别采用上述两种计算模型方法得到截面弯矩-转角关系,再得出荷载-滑移变形曲线.转角和滑移变形的关系则按式(8)计算.利用上述关系,即可将截面弯矩-转角曲线转化为构件的荷载-滑移变形曲线.
采用转动弹簧模型时,柱端截面的混凝土被划分为保护层混凝土以及核心约束混凝土;钢筋则按不考虑屈曲的钢筋本构模型建模,钢筋滑移量按Alsiwat和Saatcioglu模型计算.而采用滑移截面模型时,钢筋纤维采用Zhao和Sritharan的钢筋滑移量-应力本构模型;混凝土本构模型同上,并采用本文介绍的方法对横坐标取值进行调整.具体材料类别和本构模型的选取如表2所示.
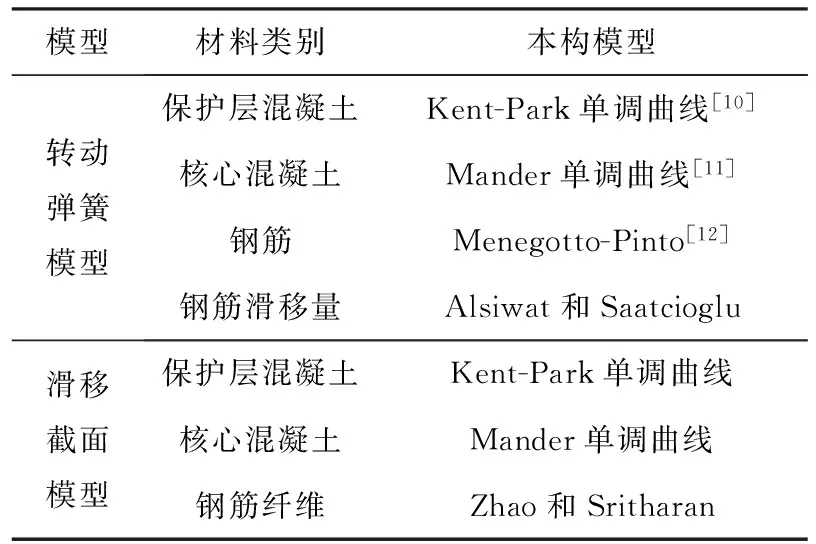
表2 分析中材料类别和本构模型的选取
5 荷载-滑移变形单调曲线
通常情况下,侧向变形试验通常只给出侧移总变形,而对分量变形的测试较少.本文选取的滑移变形试验结果,并不是通过直接测试得到的,而是通过平均曲率测试结果推算而来.平均曲率测试结果主要包含了弯曲变形和滑移变形,为了将两种变形分开,可以基于两个相邻柱段的平均曲率结果进行线性推到,以评估最外层截面的实际曲率,残余的转角可以定义为滑移转角,具体滑移分量确定可参见图4.
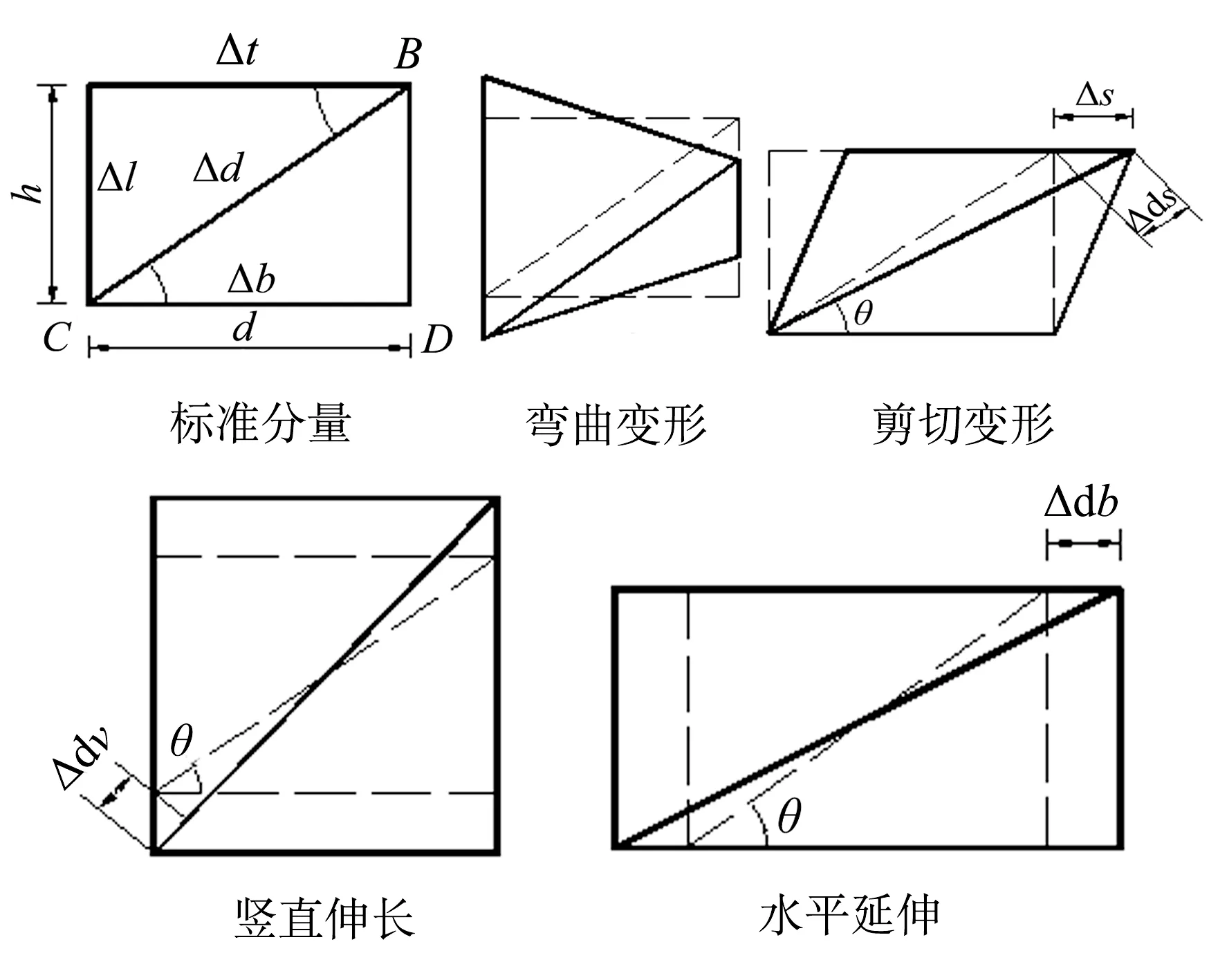
图4 标准分量的变形模式
图5和图6分别为采用转动弹簧模型和滑移截面模型得到的试件1和试件2试件的荷载-滑移变形单调曲线.
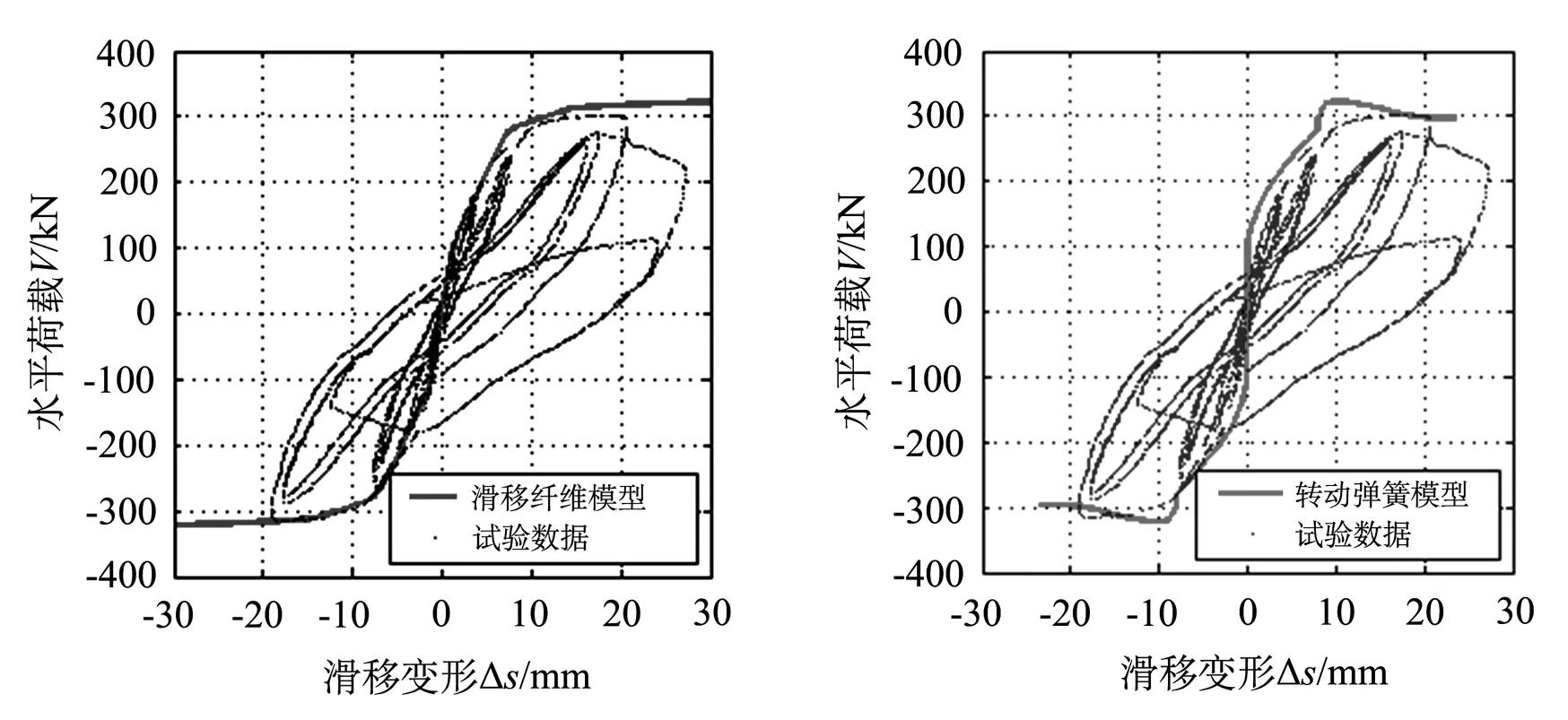
图5 试件1的荷载-滑移变形曲线
图6 试件2的荷载-滑移变形曲线
由图5(b)可见,转动弹簧模型在模拟低轴压比构件钢筋屈服前的受力变形特性较为准确.但当钢筋达到屈服强度后,会发生明显的刚度突变现象,与试验结果不符.由图6(b)可见,转动弹簧模型计算高轴压比构件的将低估构件的滑移变形.
而图5(a)和6(a)采用滑移截面模型计算构件的荷载-滑移变形反应,无论是在钢筋屈服前或钢筋屈服后,得到的结果都较转动弹簧模型更为准确.
经过系统分析,笔者认为转动弹簧模型模拟相对不准确的主要原因在于采用滑移转动中心为其邻近截面中和轴位置的假设,该假设导致低轴压柱构件屈服后的滑移变形计算结果和高轴压比柱构件滑移变形的计算结果远小于试验结果.
6 结论
本文从理论上阐述了锚固钢筋粘结-滑移的受力-变形原理,推导出钢筋滑移量-应力的显式计算表达式,基于转动弹簧模型与滑移截面模型开发了相应的计算程序,并将模拟结果与试验数据进行对比分析,结果表明采用滑移截面模型得到的构件荷载-滑移变形反应比转动弹簧模型更为准确,因此建议在钢筋混凝土构件或结构宏观分析中可优先考虑滑移截面模型.
[1]ALSIWATJM,SAATCIOGLUM.ReinforcementAnchorageSlipunderMonotonicLoading[J].ASCEJournalofStructuralEngineering,1992,118(9):2421- 2438.
[2]SEZENH,MOEHLEJP.SeismicTestsofConcreteColumnswithLightTransverseReinforcement[J].ACIStructuralJournal,2006,103(6):842- 849.
[3]SEZENH,SETZLEREJ.Reinforcementslipinreinforcedconcretecolumn[J].ACIStructuralJournal,2008,105(3):280- 289.
[4]马颖.钢筋混凝土柱破坏方式及性能研究[D].大连:大连理工大学,2012.
[5]张勤.RC柱考虑剪切作用的抗震性能和残余变形研究[D].大连:大连理工大学,2014.
[6]ELIGEHAUSENR,POPOVE,BERTEROVV.LocalBondStress-SlipRelationshipsofDeformedBarsunderGeneralizedExcitations[R].Berkeley,USA:UCB/EERC83- 23,1983.
[7]ELWOODKJ,MATAMOROSA,WALLACEJW,etal.UpdatetoASCE/SEI41ConcreteProvisions[J].EarthquakeSpectra,2007,23(3):493- 523.
[8]ZHAOJ,SRITHARANS.ModelingofStrainPenetrationEffectsinFiber-BasedAnalysisofReinforcedConcreteStructures[J].ACIStructuralJournal,2007,104(2):133- 141.
[9]SEZENH.SeismicBehaviorandModelingofReinforcedConcreteBuildingColumns[D].Berkeley:UniversityofCalifornia,Berkeley,2002.
[10]SCOTTBD,PARKR,PRIESTLEYMJN.Stress-strainbehaviorofconcreteconfinedbyoverlappinghoopsatlowandhighstrainrates[J].ASCEJournalofStructuralEngineering,1982,99(2):13- 27.
[11]MANDERJB,PRIESTLEYMJN,PARKR.Theoreticalstress-strainmodelforconfinedconcrete[J].ASCEJournalofStructuralEngineering,1988,114(8):1804- 1826.
[12]MENEGOTTOM,PINTOPE.MethodofanalysisofcyclicallyloadedRCplaneframesincludingchangesingeometryandnon-elasticbehaviorofelementsundernormalforceandbending[C].Lisbon,Portugal:IABSESymposium,1973:15- 22.
Study on Slip Deformation of Reinforced Concrete Column under Seismic Loading
ZHU Jichao1,2,WANG Xiang3,ZHAO Lihua1
(1.School of Civil and Safety Engineering,Dalian Jiaotong University,Dalian 116028,China; 2.Faculty of Infrastructure Engineering,Dalian University of Technology,Dalian 116024,China; 3.Department of Structural Engineering,University of California,San Diego,La Jolla,CA 92093- 0085,USA)
Expression of steel slip-stress is derived according to load-deformation principle of steel slip and calculation assumption of Alsiwat-Saatcioglu model. Based on rotational spring model and bar-slip fiber section model,a theoretical approach is given for the relationship of moment-rotation of end column and load-slip deformation of component.The calculating program is developed to evaluate the model adaptability.Comparison of the numerical results and experiment results validate that the load-slip deformation characteristics of reinforced concrete column component is more accurate by using adopted bar-slip fiber section model than rotational spring model.
reinforced concrete column;slip deformation;rotational spring model;bar-slip fiber section model
1673- 9590(2017)03- 0096- 05
2016- 07- 30
辽宁省自然科学基金资助项目(201602143);辽宁省教育厅高等学校科研计划资助项目(L2014193)
朱绩超(1981-),男,工程师,硕士,主要从事结构可靠度和抗震性能方面的研究E-mail:35867935@qq.com.
A
