基于最小二乘支持向量机阀控式铅酸蓄电池寿命预测

王莉,杨永辉，詹益,王晓煜，王芮琳

(1.国网辽宁省电力有限公司 电力科学研究院,辽宁 沈阳 110006; 2.大连交通大学 机械工程学院，辽宁 大连 116028; 3.大连光电通信发展有限公司,辽宁 大连 116021)*

基于最小二乘支持向量机阀控式铅酸蓄电池寿命预测

王莉1,杨永辉3，詹益2,王晓煜2，王芮琳1

(1.国网辽宁省电力有限公司 电力科学研究院,辽宁 沈阳 110006; 2.大连交通大学 机械工程学院，辽宁 大连 116028; 3.大连光电通信发展有限公司,辽宁 大连 116021)*

提出了一种新的电池寿命预测模型，即基于最小二乘支持向量机的电池寿命预测.首先阐述了最小二乘支持向量机的主要思想和基本算法，然后建立寿命预测模型，并利用此预测模型对实验数据进行了比较验证.验证结果表明，该模型在阀控式铅酸蓄电池寿命预测中具有很好的实用性，预测值与实测值能够保持很好的一致性.因此，基于最小二乘支持向量机的阀控式铅酸蓄电池寿命预测方法是切实可行的.

预测模型；支持向量机；蓄电池；寿命

0 引言

阀控式铅酸蓄电池寿命通常包括储存寿命(电池失效前在不工作的搁置状态下的储存时间)、使用寿命(电池在失效前经反复多次充放电所累积的总的可放电时间)、循环寿命(电池在失效前可反复充放电的次数总和).其中，使用最为广泛的是循环寿命.阀控式铅酸蓄电池以其性价比高，可靠性好等优点在电力通讯领域广泛应用，国内外针对铅酸蓄电池的性能研究已较为深入[1- 10]，但是对于电池的寿命预测所做的研究则并不多.所以，建立閥控式铅酸蓄电池的寿命预测模型不仅有利于电池性能的进一步深入研究，完善电池设计，更有助于电池的可靠性寿命设计.在对蓄电池的寿命预测研究中，很多文献提到了神经网络[11]、灰色理论、SVM等预测方法，其中，SVM方法表现优秀.故将此方法用于铅酸蓄电池的寿命预测应该是有效的.

最小二乘支持向量机[12- 14](Least Squares Support Vector Machines,LS-SVM)方法是采用最小二乘线性系统作为损失函数,代替传统支持向量机采用的二次规划方法,简化计算的复杂性.本

文将讨论使用最小二乘支持向量机来进行电池寿命的预测，介绍LS-SVM的数学原理及其在阀控式铅酸蓄电池寿命预测中的应用.

1 最小二乘支持向量机预测模型建立

1.1 数据预处理

若训练样本集为(xi,yi),i=1,2,…,l；x∈Rd，y∈R.支持向量机建模的主要思想[15]是：首先，用一非线性映射Ψ(·)将样本的输入空间Rd映射到特征空间Ψ(·)=(Ψ(x1),Ψ(x2),…,Ψ(xl))；然后，在这个高维特征空间中构造最优决策函数y(x)=ω·Ψ(x)+b；最后，以结构风险最小化为原则确定模型参数ω、b.

最优决策函数为

(1)

根据结构风险最小化原则,得到最小二乘支持向量机模型如下：

(2)

其中,ξi为误差变量；|ω|2为控制模型复杂度；C称为惩罚因子，为常数；b为偏差.上式对应的Lagrange函数为：

(3)

其中，αi(i=1,2,…,l)为拉格朗日乘子.

根据优化条件，即拉格朗日函数分别对四个变量求偏导：

(4)

可得

(5)

令Ψ(xi)×Ψ(xj)=Κ(xi,xj)，则优化问题转化为求解如下线性方程组：

(6)

其中,α=(α1,α2,…,αl)T，y=(y1,y2,…,yl)T.

由最小二乘法计算b和αi，得到LS-SVM决策函数为：

(7)

其中，Κ(x,xi)称为核函数，通过将输入向量从原始特征空间映射到高维特征空间,有效地解决了非线性问题.常用核函数[16]有多项式核函数、拉普拉斯核函数、柯西核函数、高斯径向核函数(RBF).

1.2 核函数的选择

多项式核函数表达式为：

(8)

RBF核函数表达式如下：

(9)

构造基于多项式和RBF的混合核函数，如下式

(10)

K(xi,yi)=(1-θ)Kp+θKr,0≤θ≤1即 则决策函数变为：

(11)

其中，θ为权重系数，xi为电压，yi为老化系数，a,b,c,d,g为待优化变量，αi为电流.

1.3 老化系数的计算

在实验中，记录了N个点的电压、容量、电流、温度，现对应每点，计算蓄电池老化系数和当前老化系数.

设第一次电压容量放电曲线中的第i点，其电压为V1i，容量为C1i，电流为I1i，温度为T1i，其老化系数β1i为1.

设第m次电压容量放电曲线中的第i点，其电压为Vmi，容量为Cmi，电流为Imi，温度为Tmi，其中V1i=Vmi.则第m次的容量为

(12)

第m次电压容量放电曲线中的第i点，其老化系数βmi为

(13)

第m次的老化系数为

(14)

1.4 数据计算

实验中可测数据分别为电压、电流、温度.所需取值均通过循环充放电完成.首先通过解线性方程组

将b，d用c，g，θ表示，随机给出一组c，g，θ做为初始值，然后使用粒子群优化算法分别进行迭代.在每一次的迭代中，粒子通过跟踪当前“极值”和全局“极值”，分别为pb和gb，来更新自己.

(16)

式中，i=1，2，…，M，M为粒子群微粒的总数，νi是粒子的速度；xi是粒子的当前位置；c1和c2是学习因子，取c1=c2=2；rand( )为0～1之间的随机数.

在粒子群优化算法中，适应度用来评价粒子的优劣，理想的适应度函数应当能够反映出不同超参数下LS-SVM的泛化能力.适应度函数为

(17)

式中，n为训练样本点的数目；yi是第i个样本的实际值；yi′为第i个样本的预测值.

1.5 误差评价指标

任何方法预测得到的结果都会与实际的值有一定差距，蓄电池的预测寿命与它的实际寿命之间的差距就是预测误差[17].预测误差应该反应出预测结果的准确性，误差值与准确性的高低成反比关系.当然对预测误差的计算有很多不同的指标，下面给出一个指标用以对本文预测的误差进行评价：

相对误差(RelativePercentageError,RPE)

(18)

其中，Qi是实际的测量值，fi是预测值.

2 实验结果及讨论

我们知道蓄电池的主要失效模式是容量衰减，预测电池寿命和预测电池的剩余容量是等价的，电池剩余容量达到失效值时所对应的充放电次数即为电池的循环寿命.蓄电池的剩余容量和电池的很多内部因素相关，其中电池的电动势是一主要因素，因此，测量蓄电池的端电压可以预测电池的剩余容量 .又电池端电压的变化与电池的健康状态(StateofHealth，SOH)有紧密联系，则这一因素有必要考虑到预测模型中.故选取电池的端电压和电池的SOH为输入特征参数，预测电池的剩余容量.电池的SOH是用于描述电池的物理性能状态的，它是电池目前所能释放的最大容量和电池全新时能释放的最大容量的比.

模型以铅酸蓄电池的SOH、端电压(U/V)为输入量，电池的剩余容量(q/Ah)为输出量，采用LS-SVM系统，核函数为由多项式核函数和RBF核函数组成的混合核函数.模型的性能评价指标采用相对误差，计算方式见式(18).

建立该模型的重要问题是权重系数θ、待优化变量a、b、c、d、g的选取.这一问题采用粒子群优化算法解决.

样本测试数据如表1所示：

实验步骤基本如下：

(1)初始化权重系数、待优化变量a、b、c、d、g；

(2)按粒子群优化算法求解权重系数θ、待优化变量a、b、c、d、g；

(3)利用LS-SVM模型中给出的算法，将参数α和b求出；

(4)把上一步得到的模型的参数代入到LS-SVM中，之后便可输入测试样本的数据，从而预测出蓄电池的剩余容量.

将模型预测值和实测值用图示直观表达如图1所示.

图1 预测值和实测值比较

从图中可以看出，使用最小二乘支持向量机原理得出的预测值和实验得出的实测值具有很高的一致性.

通过式(17)计算适应度函数为：

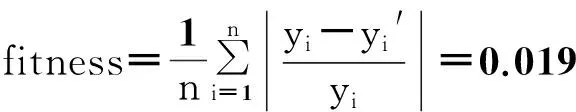
根据以上计算结果可知，模型的预测结果和实测结果的误差均不超过10%，而且适应度的计算结果为0.019 83，也表明最小二乘支持向量机在阀控式铅酸蓄电池寿命预测的应用中能得出非常准确的结果.

3 结论

系统介绍了最小二乘支持向量机原理及其在阀控式铅酸蓄电池寿命预测中的应用，通过求解线性微分方程得出最优解，提高了求解的速度.分析实验结果可知，该原理在阀控式铅酸蓄电池寿命预测中具有很好的实用性，预测值与实测值能够保持很好的一致性，在阀控式铅酸蓄电池寿命预测中具有很大的潜力.

[1]靖丽丽.阀控式铅酸蓄电池的研究进展与发展趋势[J].蓄电池,2013(1):43- 48.

[2]郑茂俊.通讯用铅酸蓄电池优化维护及修复方法研究[D].西安：西安电子科技大学,2014.

[3]任晴晴.正极添加剂对阀控密封铅酸蓄电池电化学性能的影响[D].马鞍山：安徽工业大学,2014.

[4]宋方慧.废铅酸蓄电池回收碳酸铅热分解制备氧化铅及其电化学性能研究[D].北京：北京化工大学,2015.

[5]许斌.铅酸电池结构工艺改进及性能研究[D].杭州：浙江工业大学,2015.

[6]李丽.铅酸蓄电池负极添加剂对电池性能影响的研究[D].哈尔滨：哈尔滨师范大学,2014.

[7]高林霞.柠檬酸湿法回收废铅膏过程中的杂质转化及其对电池性能影响[D].武汉：华中科技大学,2014.

[8]王少洁.蓄电池负极添加剂电化学行为研究[D].临汾：山西师范大学,2015.

[9]ALBERL,CHABROA,TORCHEUXL,etal.Improvedleadalloysforlead-acidpositivegridinelectric-vehicleapplications[J].JournalofPowerSources,1997,67(1- 2):257- 265.

[10]KIESSLINGR.Lead/acidbatteriesforload-levellingapplications[J].JournalofPowerSources,1987,19(2/3):227- 230.

[11]张金国,王小君,朱洁,等.基于MIV的BP神经网络磷酸铁锂电池寿命预测[J].电源技术,2016(1):50- 52.

[12]VAPNIKVN.StatisticalLearningTheory[M].NewYork:JWiley,1998.

[13]VAPNIKVN.TheNatureofStatisticalLearningTheory[M].NewYork:SpringerVerlag,1999.

[14]顾燕萍,赵文杰,吴占松.最小二乘支持向量机的算法研究[J].清华大学学报(自然科学版),2010(7):1063- 1071.

[15]丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011(1):2- 10.

[16]邬啸,魏延,吴瑕.基于混合核函数的支持向量机[J].重庆理工大学学报(自然科学),2011(10):66- 70.

[17]王真真.误差相关核回归[D].济南：山东大学,2012.

Life Prediction of Valve Regulated Lead-Acid Battery based on Least Square Support Vector Machine

WANG Li1,YANG Yonghui3,ZHAN Yi2,WANG Xiaoyu2,WANG Ruilin1

(1.Electric Power Science Research Institute,Liaoning Electric Power Co.,Ltd,Shenyang 110006,China; 2.School of Mechanical Engineering,Dalian Jiaotong University,Dalian 116028,China; 3.Dalian Photoelectric Communication Development Co., Ltd,Dalian 116028,China)

A new battery life prediction model is proposed based on least square support vector machine.The main idea and basic algorithm of least square support vector machine is expounded,and the life prediction model is established.The experimental data were compared and validated by using this prediction model.The verification results show that the model has good practicability in the valve regulated lead-acid battery life prediction,and the predictive value can be maintained in good agreement with the measured values.Therefore,based on the least square support vector machine,the life prediction method of valve regulated lead-acid battery is feasible.

prediction model;support vector machine;battery;life

1673- 9590(2017)03- 0116- 04

2016- 11- 23

国网电力科技计划资助项目

王莉(1963-),女，教授级高级工程师,学士，主要从事环境保护领域的研究E-mail:wl_dky@126.com.

A