含Kerr缺陷函数型光子晶体低阈值双稳态的对比研究

王 筠

(湖北第二师范学院 物理与机电工程学院 信息科学与技术研究院， 武汉 430205)

含Kerr缺陷函数型光子晶体低阈值双稳态的对比研究

王 筠*

(湖北第二师范学院 物理与机电工程学院 信息科学与技术研究院， 武汉 430205)

运用非线性传输矩阵法对比研究含Kerr缺陷余弦函数型和Sinc函数型光子晶体的光学双稳态.结果表明，选取中心层为Kerr缺陷层的对称结构可以大大降低双稳态阈值；在缺陷层光学厚度不变的前提下，减小中心缺陷层线性折射率而增大两侧介质层周期数均可以实现更低双稳态阈值；研究还表明，在介质层光学厚度相同的前提下，介质层折射率分布函数选取余弦函数形式较Sinc函数形式能够实现更低阈值.

非线性； 光学双稳态； 传输矩阵； Kerr介质； 函数光子晶体

自1987年Yablonovitch和John提出光子晶体的概念以来[1]，光子晶体已成为光电子材料的一个重要研究领域.一维光子晶体由于其结构简单，易于实现而受到广泛关注，如果将Kerr介质缺陷引入其中，将会产生诸如光限制、光开关、光二极管和光学双稳态等奇异的非线性现象[2-13].由于Kerr介质的折射率与其中的光强有关，当入射光强变化时，其折射率也随之改变，所以常规的传输矩阵法不适用，有文献提出非线性传输矩阵法[3].研究发现，在一维含缺陷光子晶体中，缺陷模频率依赖于缺陷层折射率和厚度，当缺陷层中引入Kerr介质时，缺陷模频率将随着入射光强而改变，于是，人们可以在这个缺陷模频率附近调节入射光频率使该结构相对于入射光产生正或负反馈，光学双稳态将会出现[2-13].由于光学双稳态在量子计算和量子通讯中的全光开关、全光存储、全光三极管和全光逻辑电路中的潜在应用而备受关注[3-12].

有文献[13-16]提出一种新型的函数光子晶体的概念，这种光子晶体的介质层折射率是随空间位置变化的周期函数，光波在其中沿曲线路径传播.已有文献[15-17]研究了一维折线型、阶梯型和正弦函数型光子晶体的光学传输特性.研究发现，加入缺陷后可获得宽阔的光子禁带[17-18]，隧穿缺陷模频带狭窄且附近场分布高度局域；如果将非线性缺陷引入函数型光子晶体中，可以预见在获得极宽阔的光子禁带的同时，通过调节相应参量可以实现光学双稳态，这是因为禁带中的缺陷模频带狭窄，缺陷模频率处的电磁波模式态密度非常大，这将十分有利于非线性效应的产生.本文将Kerr缺陷引入到余弦函数型光子晶体中，构成这类光子晶体的非线性微腔，并与Sinc函数型光子晶体作对比研究，探讨可否通过选择适当的介质层折射率分布函数的方式实现降低双稳态阈值，为低开关阈值光学双稳态器件设计新方法提供理论参考.

1理论模型

本文主要研究左右两侧由函数折射率介质层A、B交替组成的两个半有限光子晶体(BA)m和(AB)n，在二者之间是缺陷层D所构成的对称周期结构(BA)mD(AB)n，其中m、n是周期数.A、B介质层折射率随空间位置变化，为了考察这两个介质层采用不同折射率分布函数对非线性光学双稳态阈值的影响，本文分别对A、B介质层折射率采用余弦函数型和Sinc函数型.在A、B介质层折射率随空间位置按余弦函数变化的关系式是

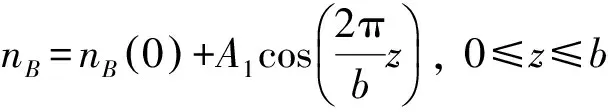
(1)

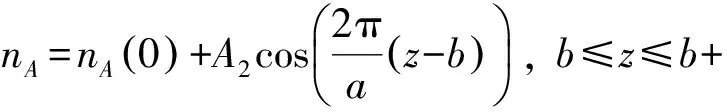
(2)

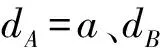
当A、B介质层折射率随空间位置按Sinc函数变化的关系式是

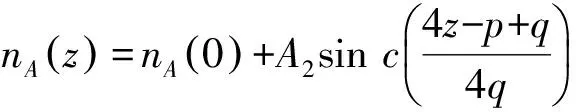
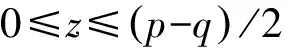
(3)

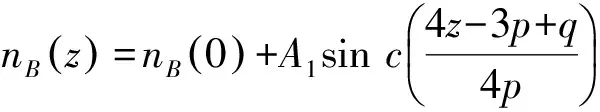
(p-q)/2≤z≤p.

(4)

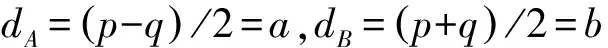
缺陷层D构成微腔，填充的是具有Kerr效应的非线性介质，Kerr介质的折射率分布为

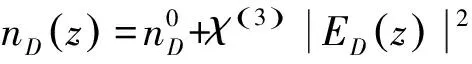
(5)

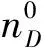
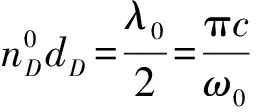
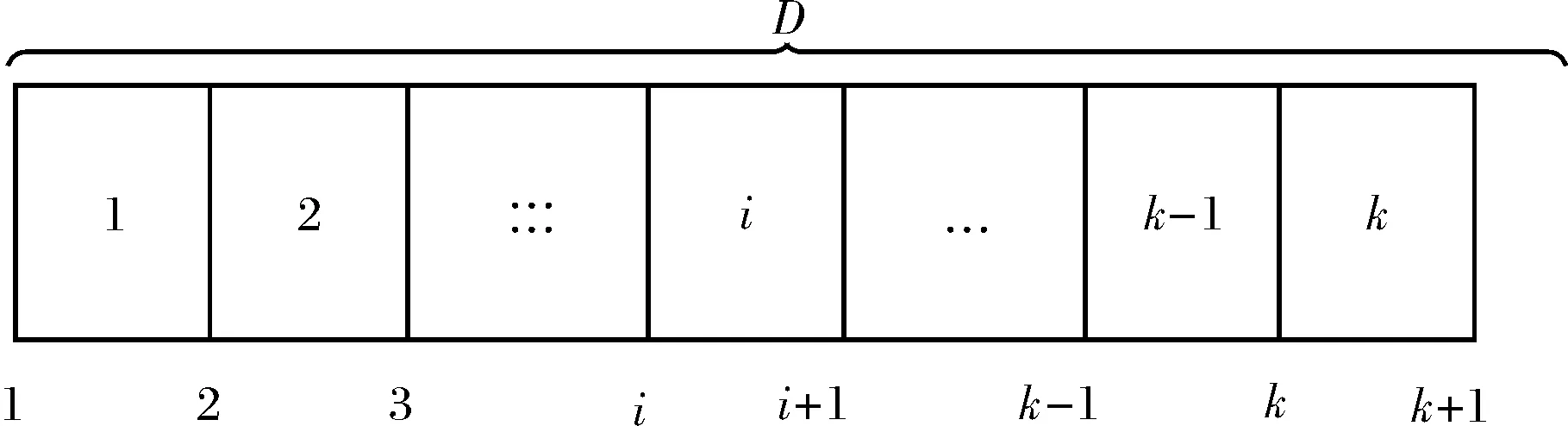
图1 D层分为k个子层示意图Fig.1 The layer D is divided as k sublayers

2计算方法

2.1非线性传输矩阵法

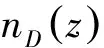
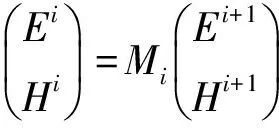
(6)

其中，Mi是第i个子层的特征矩阵；于是第1个子层左侧边界上的切向场量与第k个子层右侧边界上的切向场量间的关系式是：

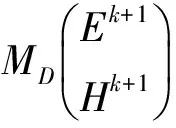
(7)

根据电磁场边界条件可推得入射波场量与透射波场量间的关系式：

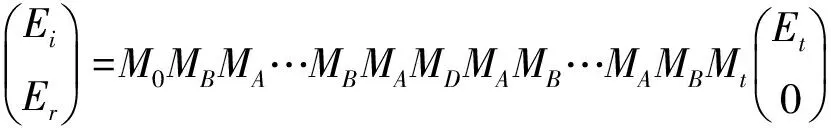
(8)

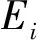
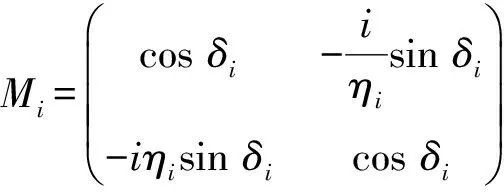
i=A，B，1，2，…，k-1，k.

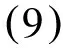
2.2非线性微腔内部场分布

由(4)～(7)式可得非线性微腔D内第i个子层距离入射面z处电场强度表示式

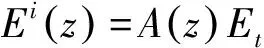
(10)

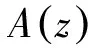
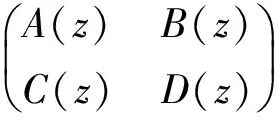
的矩阵元；给出透射波电场强度，根据(8)式就可以求得非线性微腔第i个子层内任一点处的场分布.

3数值计算与分析

3.1线性微腔传输特性

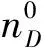
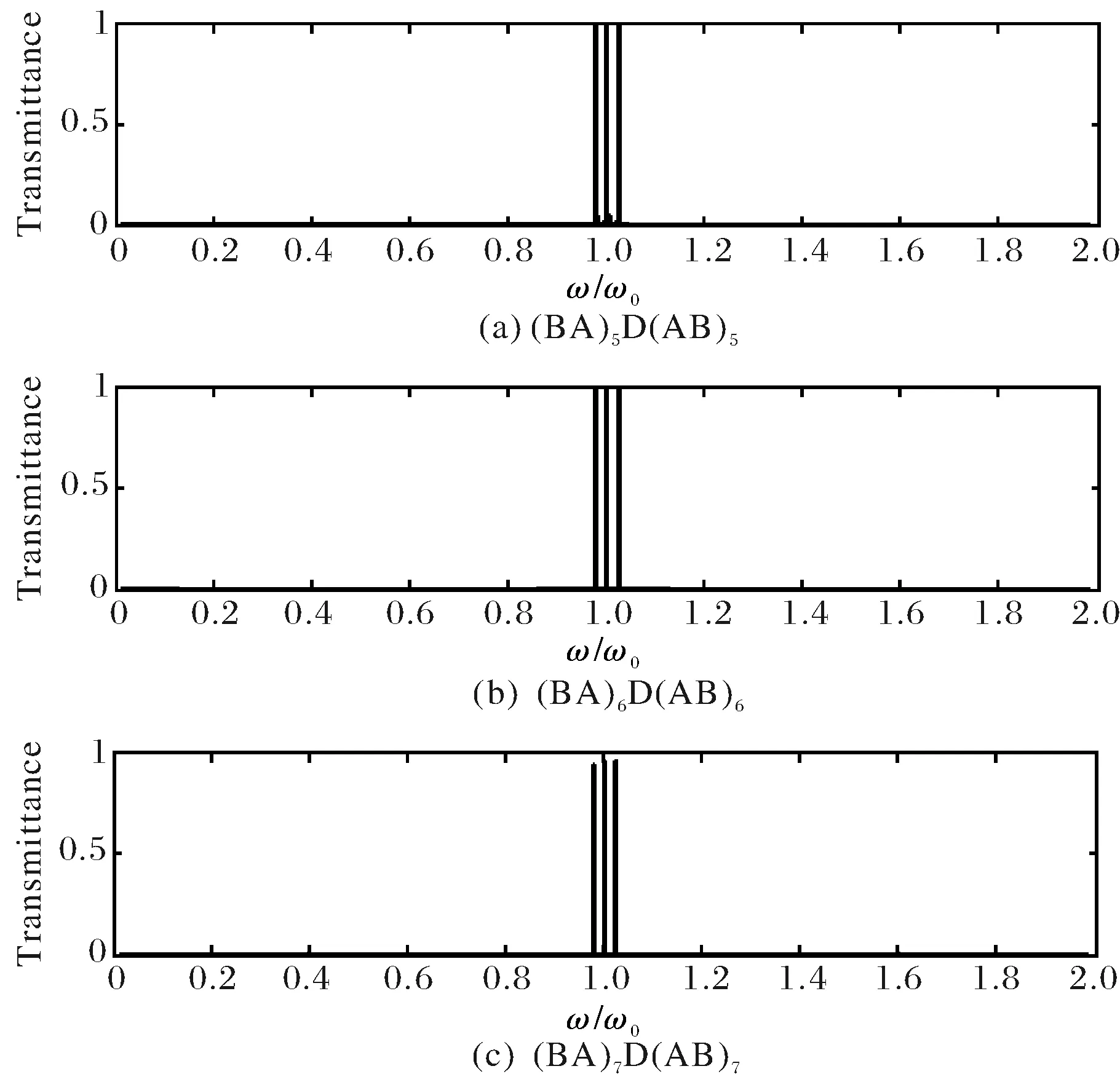
图2 余弦函数型光子晶体不同周期数的透射谱Fig.2 Transmission spectra of Cosin function photonic crystal of different period number

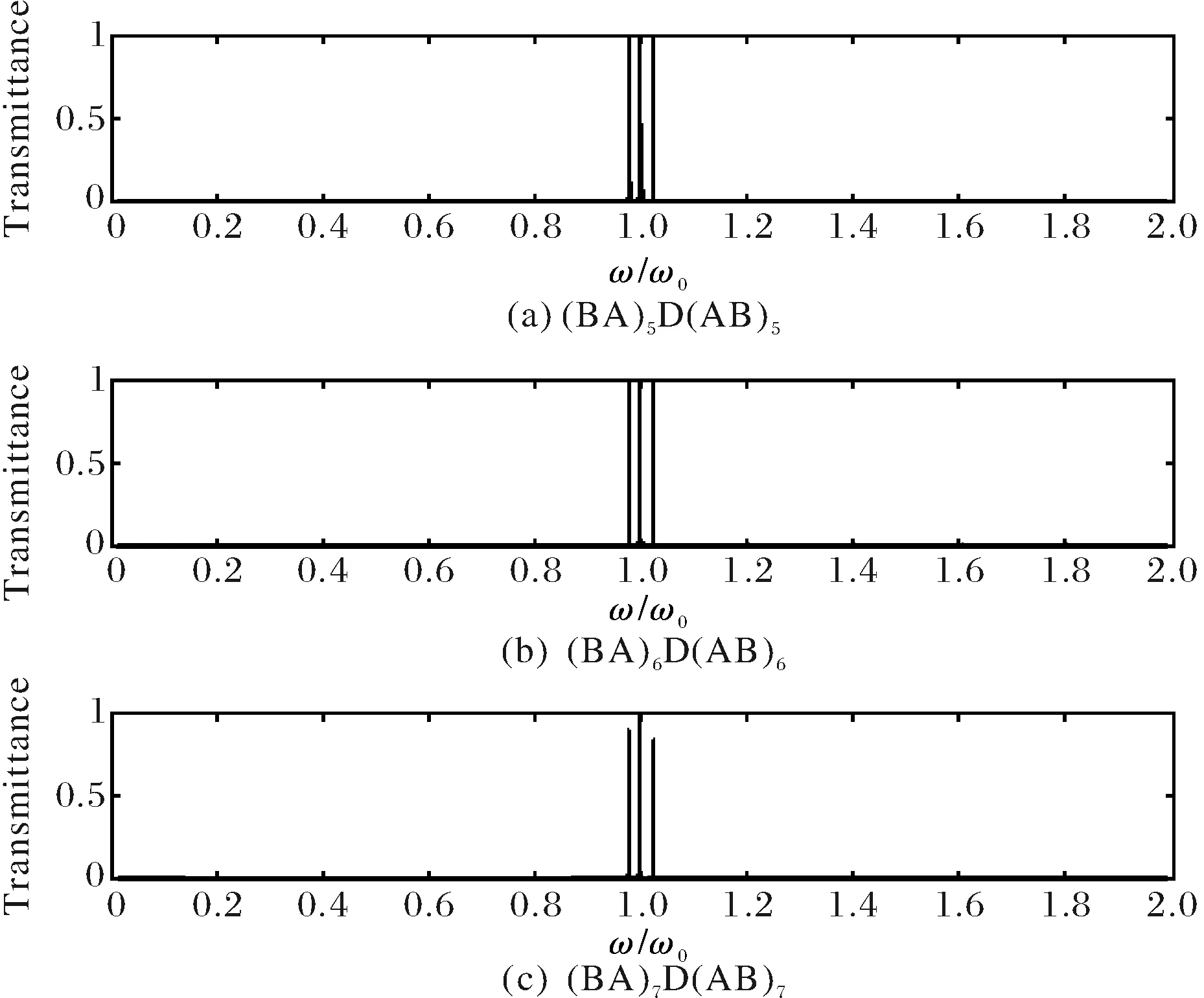
图3 Sinc函数型光子晶体不同周期数的透射谱Fig.3 Transmission spectra of Sinc function photonic crystal of different period number

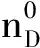
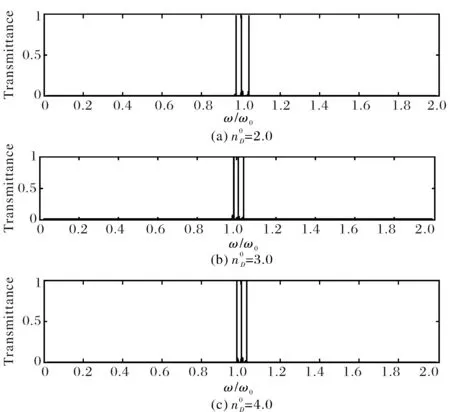
图4 周期结构(BA)5D(AB)5余弦型光子晶体不同缺陷层的透射谱Fig.4 Transmission spectra of Cosin function photonic crystal (BA)5D(AB)5in different linear cavity

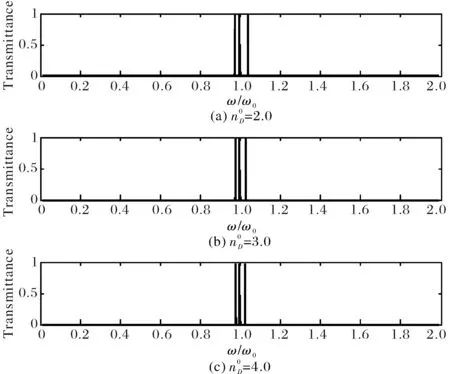
图5 周期结构(BA)5D(AB)5Sinc型光子晶体不同缺陷层的透射谱Fig.5 Transmission spectra of Sinc function photonic crystal(BA)5D(AB)5in different linear cavity

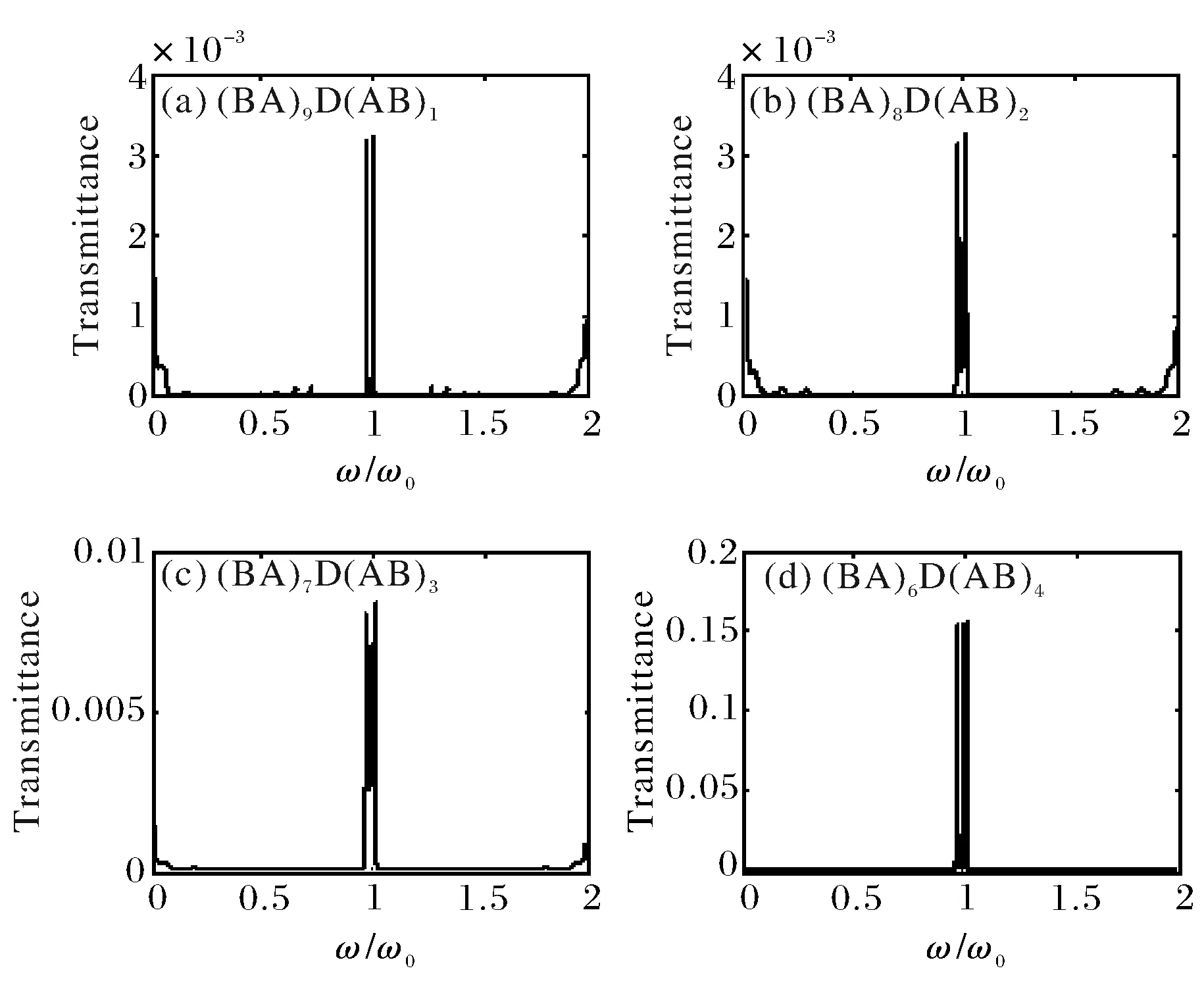
图6 不同位置缺陷层余弦函数型光子晶体的透射谱Fig.6 Transmission spectra of different position defect layers of Cosin function photonic crystal

3.2非线性微腔的光学双稳态特性

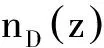
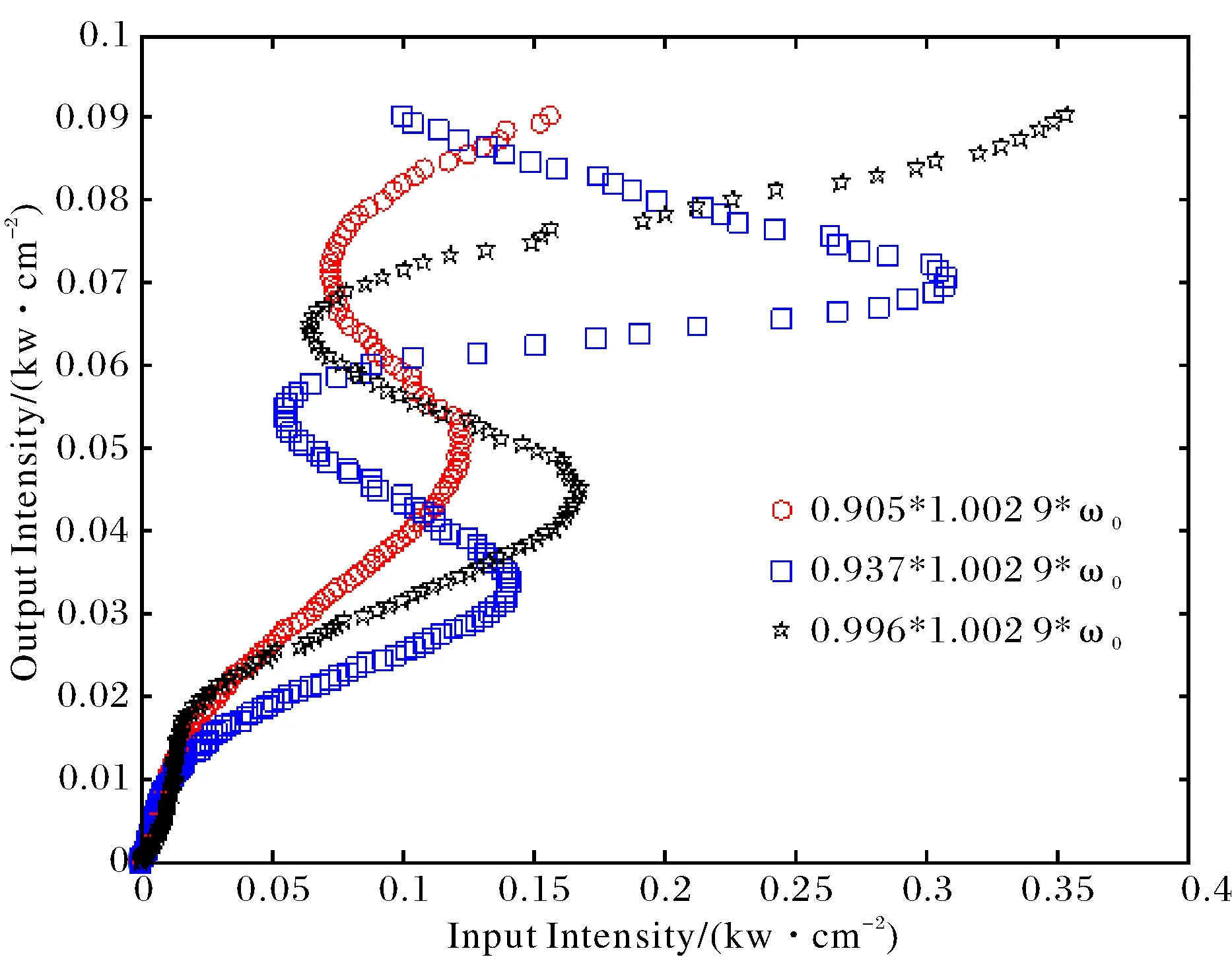
图7 不同入射圆频率时余弦函数型光子晶体 (BA)5D(AB)5的输入和输出的关系曲线Fig.7 Relationship between input and output of (BA)5D(AB)5of Cosin function photonic crystalin different incident circular frequency

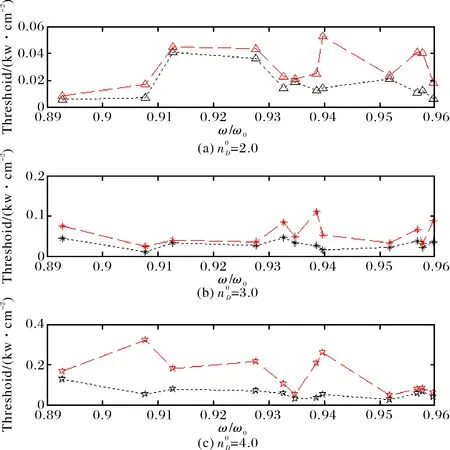
图8 不同非线性微腔余弦函数型 光子晶体双稳态阈值比较Fig.8 Comparison of bistable threshold of different nonlinear micro cavity of Cosin function photonic crystal

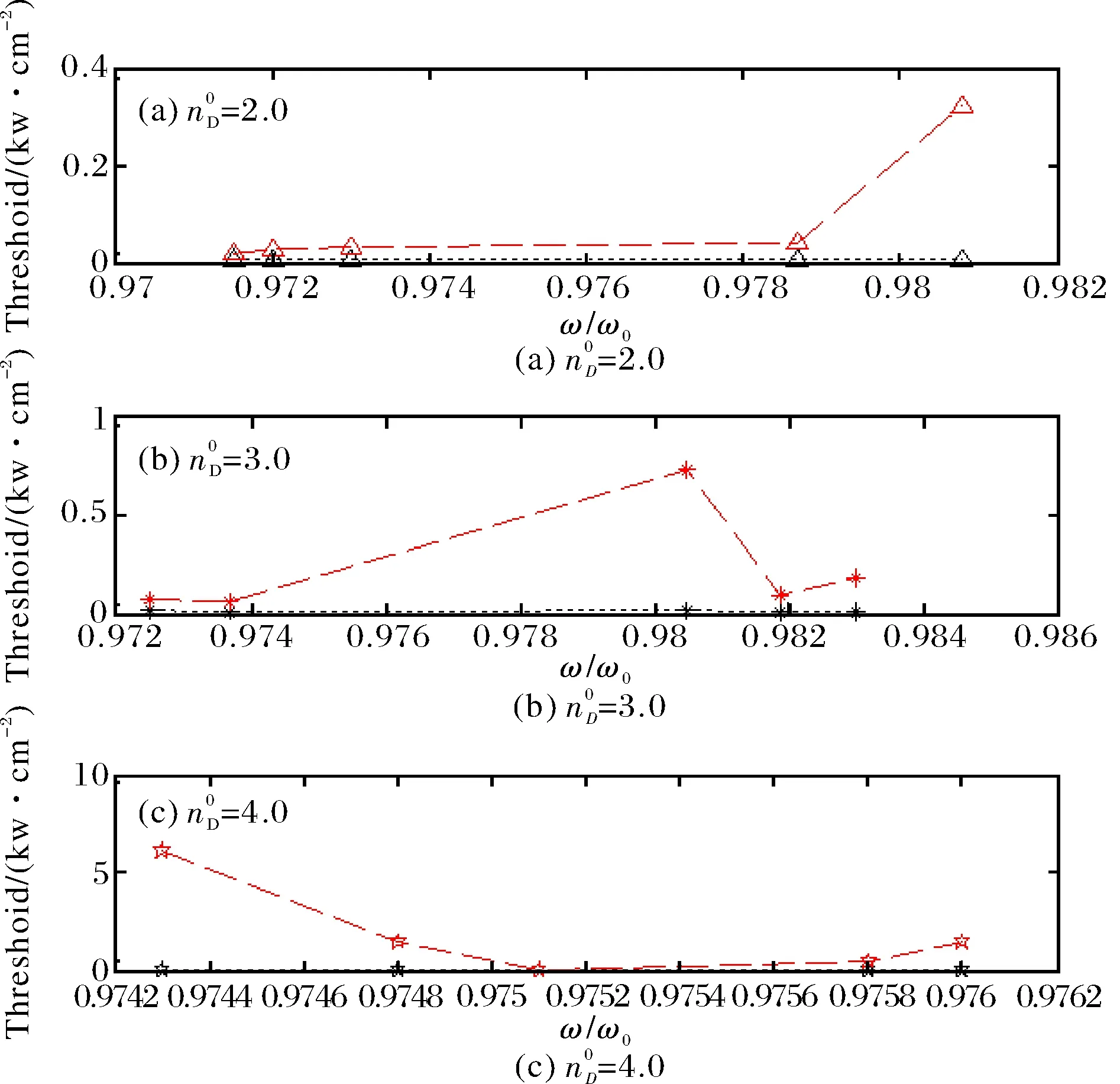
图9 不同非线性微腔Sinc 函数型光子晶体双稳态阈值比较Fig.9 Comparison of bistable threshold of different nonlinear micro cavity of Sinc function photonic crystal

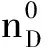
由前一节知，微腔D两侧周期结构(BA)m和(AB)m的周期数m增大会使得D内场强幅值增大，这将十分有利于非线性效应的产生[3]，为了验证这一猜想，在图10和图11中计算得到余弦型和Sinc型光子晶体在各自的中心隧穿模(ωm=1.0029ω0、ωm=0.9949ω0)附近的高低双稳态阈值，在图10 和图11中可知：随着周期数m的增大，双稳态阈值总体上的确是趋于减小.将图10与图11进行比较还可以发现：余弦型光子晶体光学双稳态阈值较Sinc函数型光子晶体要低，实现光学双稳态更容易，这与上面的结论一致.

由图6可知，当缺陷层D偏离该周期结构中心位置时，中心隧穿模透射率急剧减小，这将十分不利于非线性效应的产生，为了弄清楚这一情况，在图12中计算了余弦型光子晶体的缺陷层D偏离中心位置的三种不同周期结构的光学双稳态高、低阈值，其中红色数据点代表高阈值，蓝色数据点代表低阈值.比较后可以发现，随着D偏离中心位置越远，光学双稳态阈值的确趋于增大.

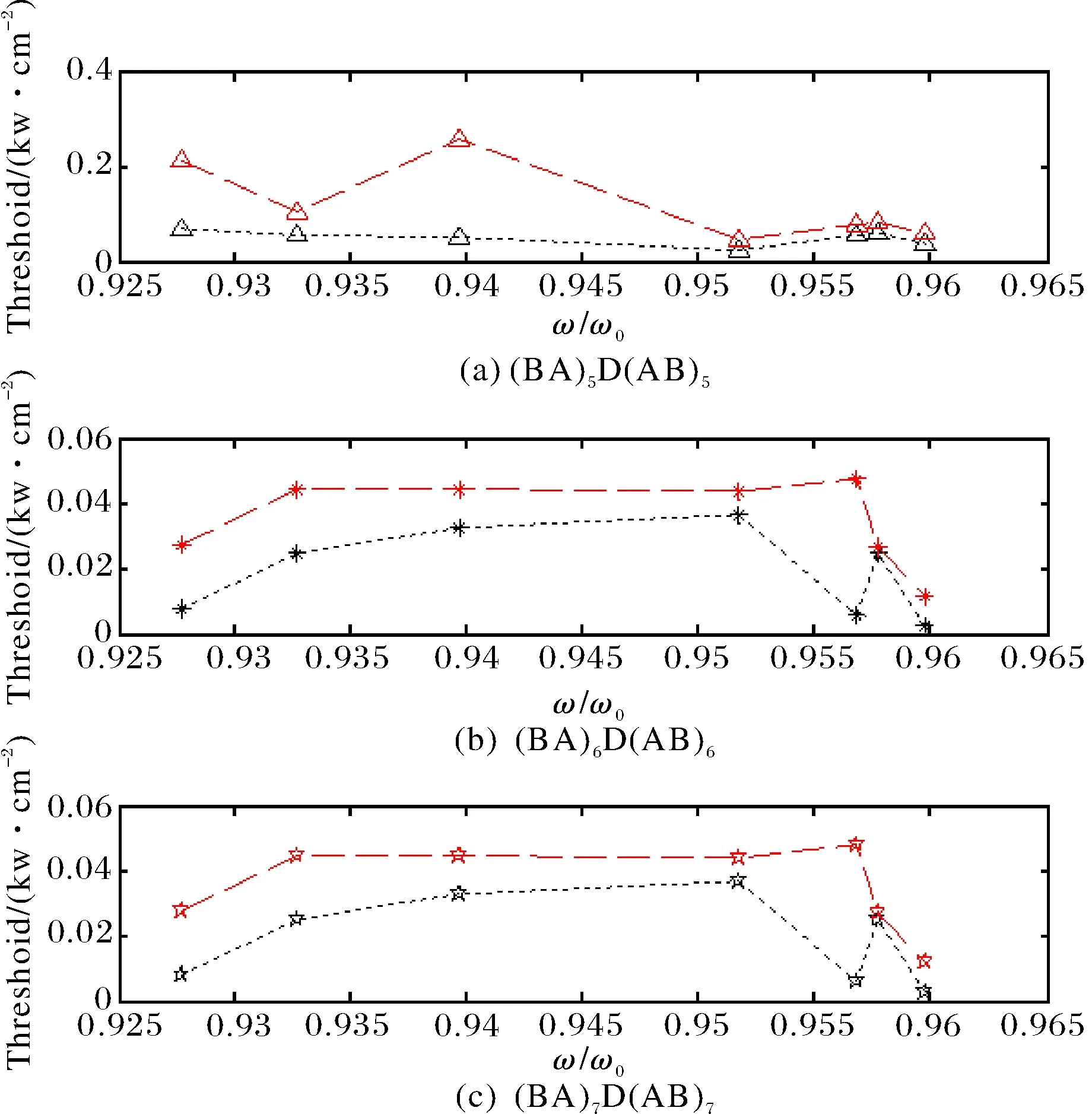
图10 不同周期数余弦函数型光子晶体双稳态阈值比较Fig.10 Comparison of bistable threshold of different periodic number of Cosin function photonic crystal

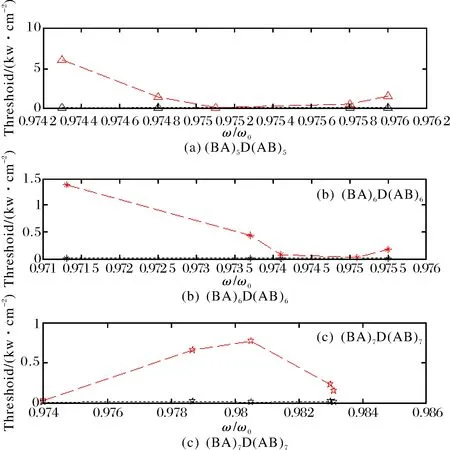
图11 不同周期数Sinc函数型光子晶体双稳态阈值比较Fig.11 Comparison of bistable threshold of different periodic number of Sinc function photonic crystal

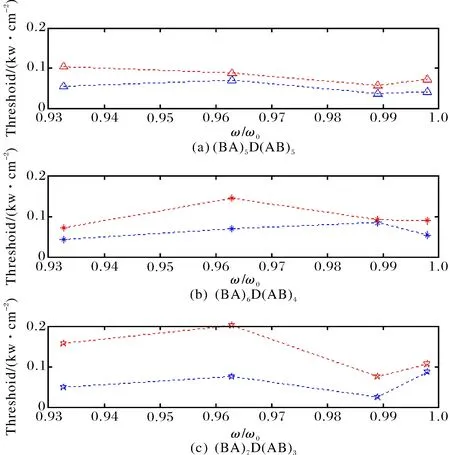
图12 3种不同周期结构余弦型 光子晶体的双稳态阈值比较Fig.12 Comparison of bistable threshold of three different periodic structures of cosin function photonic crystal

4结论

本文运用非线性传输矩阵法对比研究了含Kerr缺陷的余弦函数型和Sinc函数型光子晶体的光学双稳态.结果表明，以缺陷层为中心的对称结构可以实现更低阈值；并且在缺陷层光学厚度不变的条件下，减小中心缺陷层线性折射率而增大两侧介质层周期数均可以进一步降低双稳态阈值；研究还表明，在介质层光学厚度相同的前提下，介质层折射率选取余弦函数形式较Sinc函数形式能够实现更低阈值.

[1] YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Physical Review Letters， 1987， 58(20): 2059-2062．

[2] GIBBS H M， MCCALL S L， VENKATESANT T N C. Differential gain and bistablity using a sodium-filled Fabry-Perot Interferometer[J]. Phys Rev Lett， 1976， 36:1135-1138．

[3] HE J， CADA M. Combined distributed feedback and Fabry-Perot structures with a phase-matching layer for optical bistable devices[J]. Appl Phys Lett，1992，61(18): 2150-2152．

[4] DAWES A M C， ILLING L， CLARK S M，et al.All-optical switching in rubidium vapor[J]. Sci 2005， 29:672-674．

[5] OROZCO L A， KIMBLE H J， ROSENBERGER A T， et al.Single-mode instability in optical bistability[J]. Phys Rev A， 1989， 39:1235-1241．

[6] SZOKE A， DANEU V， GOLDHAR J，et al. Bistable optical element and its applications[J]. Appl Phys Lett， 1969， 15:376-388．

[7] JAFARZADEH H， SAHRAI M， JAMSHIDI-GHALEH K. Controlling the optical bistability in a Λ-type atomic system via incoherent pump field[J]. Appl Phys B， 2014， 117: 927-933．

[8] SCALORA M， DOWLING J P， BOWDEN C M， et al. Bloemer optical limiting and switching of ultrashort pulses in nonlinear photonic band gap materials[J]. Phys Rev Lett， 1994， 73:1368-1377．

[9] TAKEDA H，JOHN S. Self-consistent Maxwell-Bloch theory of quantum-dot-population switching in photonic crystals[J]. Phys Rev A， 2011， 83:053811(1-11)．

[10] LIU N H， ZHU S Y， CHEN H. Localized electromagnetic modes of one-dimensional modulated nonlinear photonic band-gap structures[J]. Phys Rev B， 2001， 64(16)：165105(1-10)．

[11] 陈宪锋， 沈小明， 蒋美萍， 等. 非线性Bragg微腔的双稳态研究[J].光子学报，2007， 36(4): 613-616．

[12] 姜迎新， 方云团. 利用光子隧穿效应实现高Q/V值微腔和光学双稳态[J].人工晶体学报， 2011， 40(3):796-800．

[13] WU X Y， ZHANG B J，YANG J H， et al. Function photonic crystals[J]. Physica E， 2011， 43(9):1694-1700．

[14] 王光怀， 王清才， 吴向尧， 等.一维函数光子晶体的研究[J].物理学报， 2012， 61(13):134208(1-10)．

[15] WU X Y， ZhANG B J， YANG J H， et al. The characteristic of light transmission of function photonic crystals[J]. Physica E， 2012， 44(7):1223-1229．

[16] 巴 诺， 吴向尧， 王 婧， 等.一维函数型光子晶体的光学传输特性[J].中国激光， 2012， 39(6):0606001(1-7)．

[17] 王 筠. 色散缺陷对Sinc函数型光子晶体带隙的影响[J].中国激光， 2015， 42(4):0406001(1-9)．

[18] 王 筠， 冯国强， 刘 丹， 等. Sinc 函数型光子晶体非线性微腔的光学双稳态[J].激光与光电子学进展， 2016， 53(1):011901(1-13)．

A comparative study on low threshold bistable stateof functional photonic crystal with Kerr defect

WANG Yun

(School of Physics and Electrical and Mechanical Engineering,Hubei University of Education Institute of Information Science and Technology, Wuhan 430205)

The nonlinear transfer matrix method is used to study the optical bistable characteristics of cosine function and sinc function photonic crystal with Kerr defect in this paper. The results show that the bistable thresholds are greatly reduced by choosing the symmetrical structure of the center layer as the Kerr defect layer. And under the condition that the optical thickness of the defect layer is constant, the lower bistable thresholds are able to be achieved when the linear refractive index of the center defect layer is decreased and the cycle number of both sides of the medium layer are increased. The result also shows that the lower threshold values is able to be realized by refractive index distribution function of dielectric layer selected as the form of cosine function than Sinc function under the same optical thickness of the dielectric layer.

nonlinear; optical bistability; transfer matrix; Kerr medium; function photonic crystal

2016-05-21.

湖北省自然科学基金项目(2015CFC885)．

1000-1190(2017)01-0028-07

O437

A

*E-mail: wangyun.2007.6.5@163.com．