面向特征选择问题的协同演化方法
2017-06-01滕旭阳董红斌孙静
滕旭阳,董红斌,孙静
(哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨 150001)
面向特征选择问题的协同演化方法
滕旭阳,董红斌,孙静
(哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨 150001)
特征选择技术是机器学习和数据挖掘任务的关键预处理技术。传统贪婪式特征选择方法仅考虑本轮最佳特征,从而导致获取的特征子集仅为局部最优,无法获得最优或者近似最优的特征集合。进化搜索方式则有效地对特征空间进行搜索,然而不同的进化算法在搜索过程中存在自身的局限。本文吸取遗传算法(GA)和粒子群优化算法(PSO)的进化优势,以信息熵度量为评价,通过协同演化的方式获取最终特征子集。并提出适用于特征选择问题特有的比特率交叉算子和信息交换策略。实验结果显示,遗传算法和粒子群协同进化(GA-PSO)在进化搜索特征子集的能力和具体分类学习任务上都优于单独的演化搜索方式。进化搜索提供的组合判断能力优于贪婪式特征选择方法。
特征选择;遗传算法;粒子群优化;协同演化:比特率交叉
特征选择在数据挖掘和机器学习中不仅可以减少数据的维度,降低所需处理的数据量,而且还可以提升某些学习算法的表现[1],比如:分类学习、聚类、回归问题和时间序列预测等。然而维数据特征选择面临着特别庞大的搜索空间等,当存在n维特征时解的搜索空间为2n,因此穷举搜索是不可行的[2]。特征选择方法大致可分为3类:过滤式(filter)、包裹式(wrapper)和嵌入式(embedding)[3]。过滤式方法与具体学习方法无关,主要依据数据的内在属性对特征进行过滤,再用选择出的特征训练模型。包裹式方法将最终要使用的学习器的学习性能作为评价子集评价标准。嵌入式方法将特征选择过程与学习器训练过程融为一体,两者在同一过程中优化。wrapper方法对于具体学习器效果好,但其计算代价高,泛化能力差。filter方法虽然在具体学习方法中精度低于wrapper方法,但其泛化能力强,计算效率高,在大规模数据集上更加适用。因此,本文选用基于信息熵度量的filter评价方式。
为了保证搜索的高效,许多学者选择了贪婪式搜索方法来选择子集,代表性方法有基于信息增益的方法(IG)[4]和基于信息比率的方法(GR)[5]。然而贪婪方法无可避免地导致其结果为局部最优,因为其在选择过程中仅考虑当前轮的单个最佳或最差特征[6]。为了解决上述问题,全局搜索的方式则成为特征选择问题中一种有效的寻优方式。演化计算作为一种具有良好全局搜索能力的代表技术近年来被越来越多地使用在特征选择技术中[7]。随着各个领域内数据维度不断地增加,自2007后遗传算法(genetic algorithm,GA)与粒子群优化(particle swarm optimization,PSO)成为特征选择进化搜索策略中两个主流的全局搜索方法,特别是PSO方法因其搜索速度得到了广泛的使用。Peng等[8]在2005年提出了最大相关最小冗余的特征选择方法(mRmR),该方法使用了贪婪式搜索方式。在2011年和2012年学者们验证了使用mRmR进行度量并采取群智能进化搜索的方式可以获得更优的特征子集[9,10]。
虽然在特征选择问题中演化算法的搜索能力优于贪婪式搜索,但不同的演化算法自身也存在局限性。因此更多的学者开始研究协同演化的方法,其中包括策略的协同[11]和种群的协同[12]。本文选用GA与PSO两种进化种群的协同。PSO 的优势在于对解的记忆能力强及高效的收敛速度,但该方法极容易陷入到局部最优解,表现出极强的趋同性和较低的种群多样性。GA方法中染色体之间共享信息,种群较为均匀地移动并保持多样性,但其收敛速度相对较慢。因此,本文提出了一种面向特征选择问题的协同演化方法(GA-PSO),演化过程中既保证了全局搜索能力以防止陷入局部最优,又提升了演化速度。
1 基础知识
1.1 特征选择
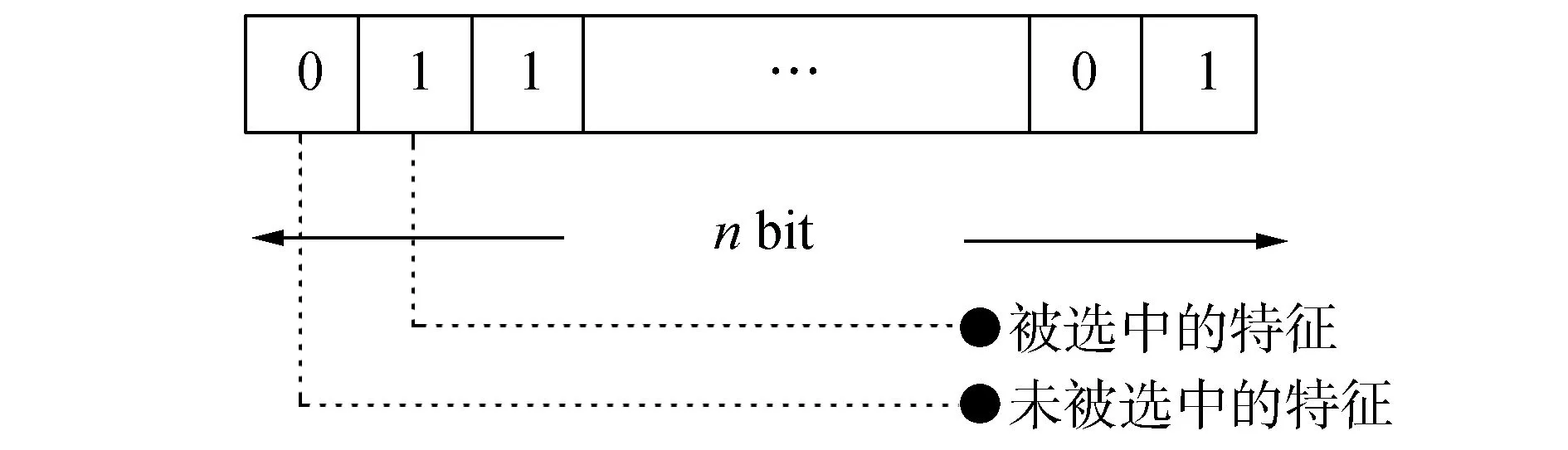
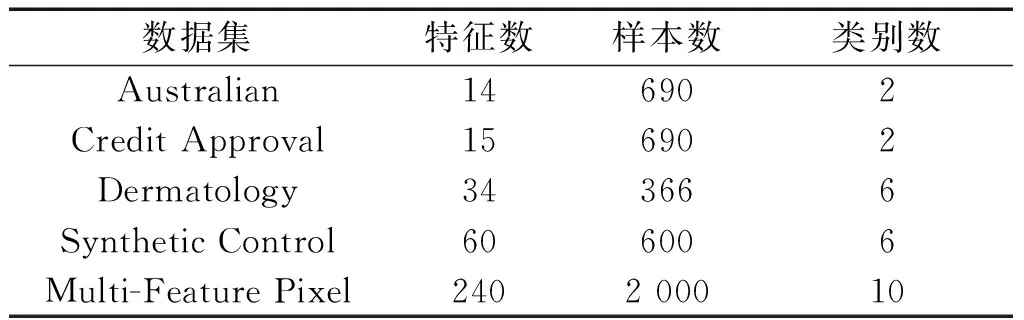
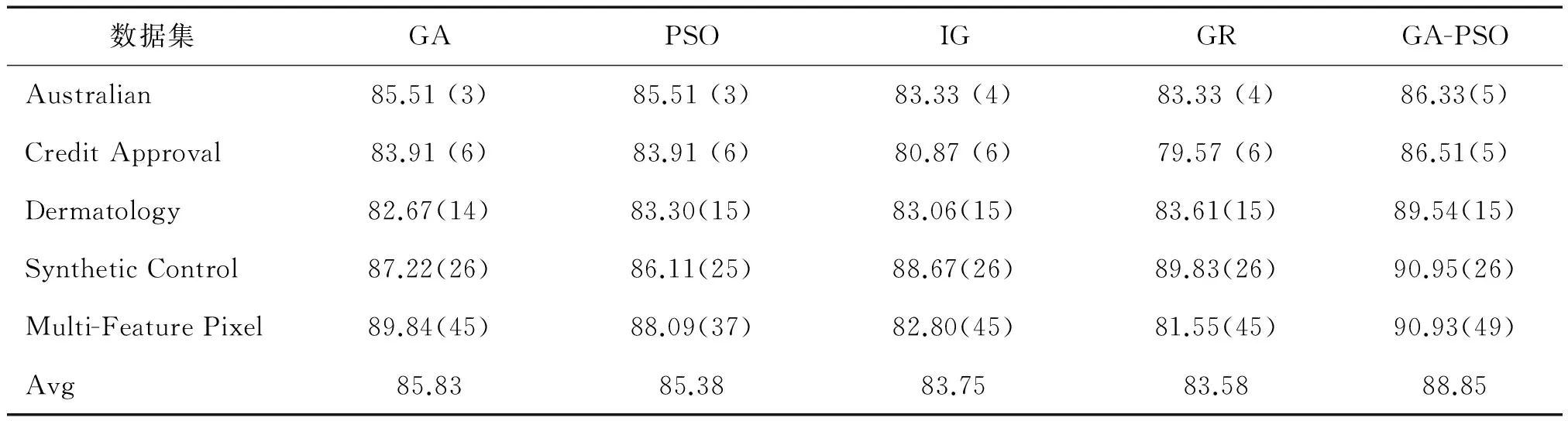
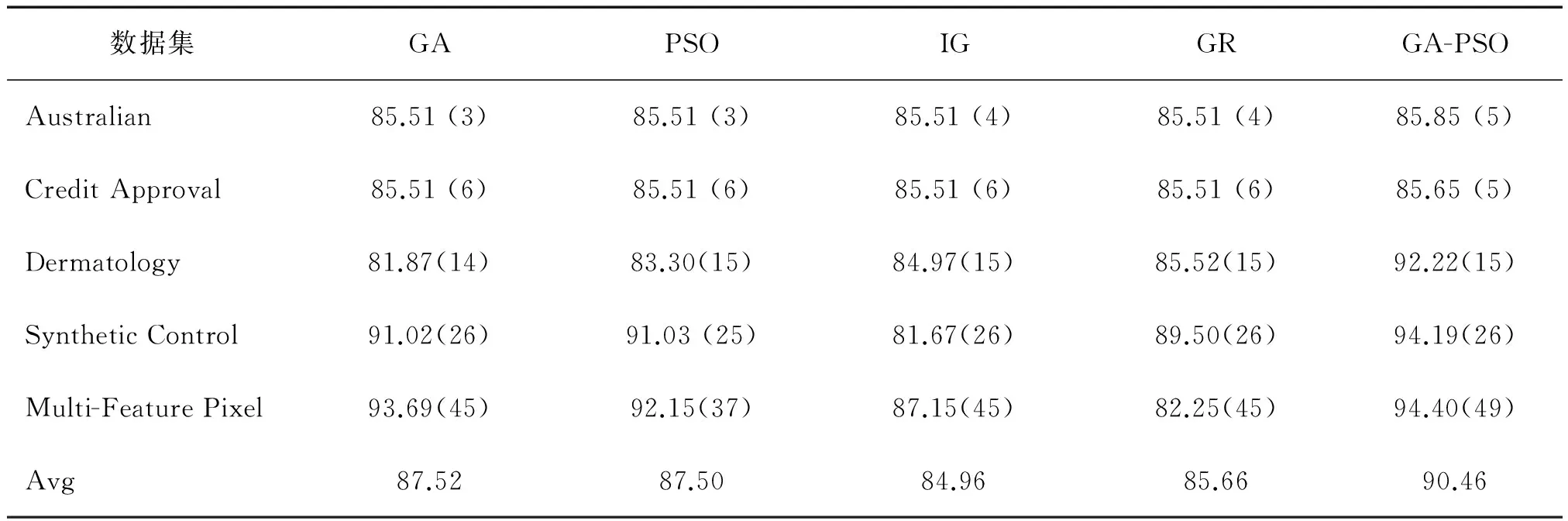
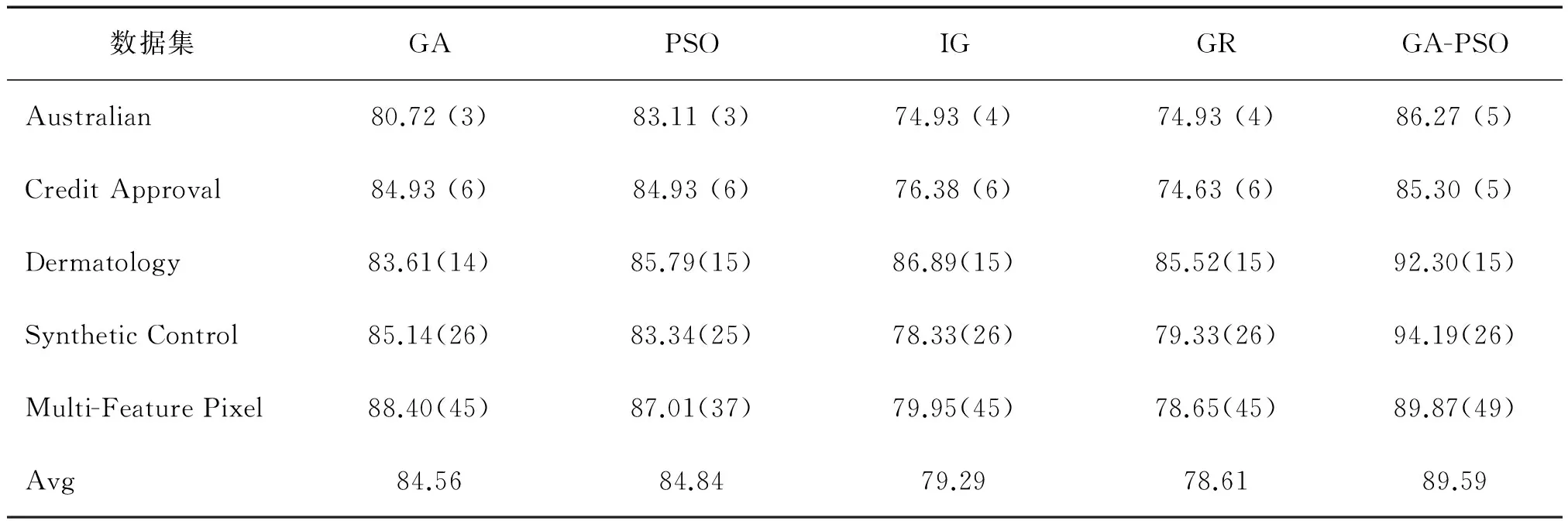
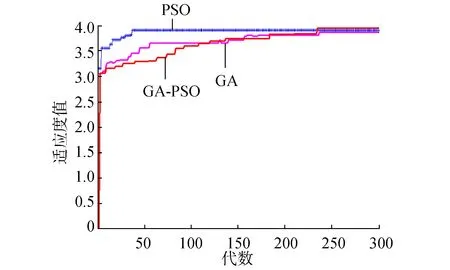
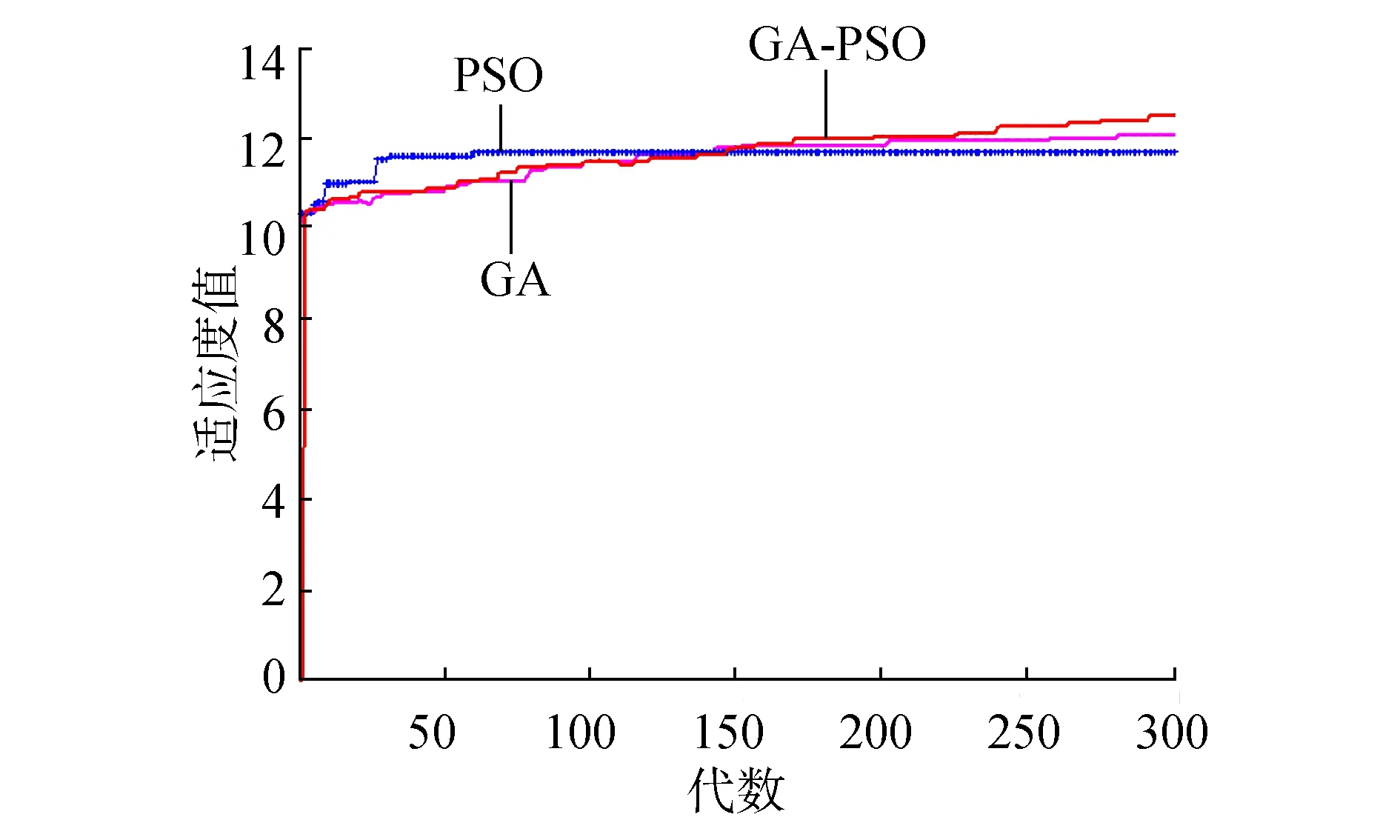
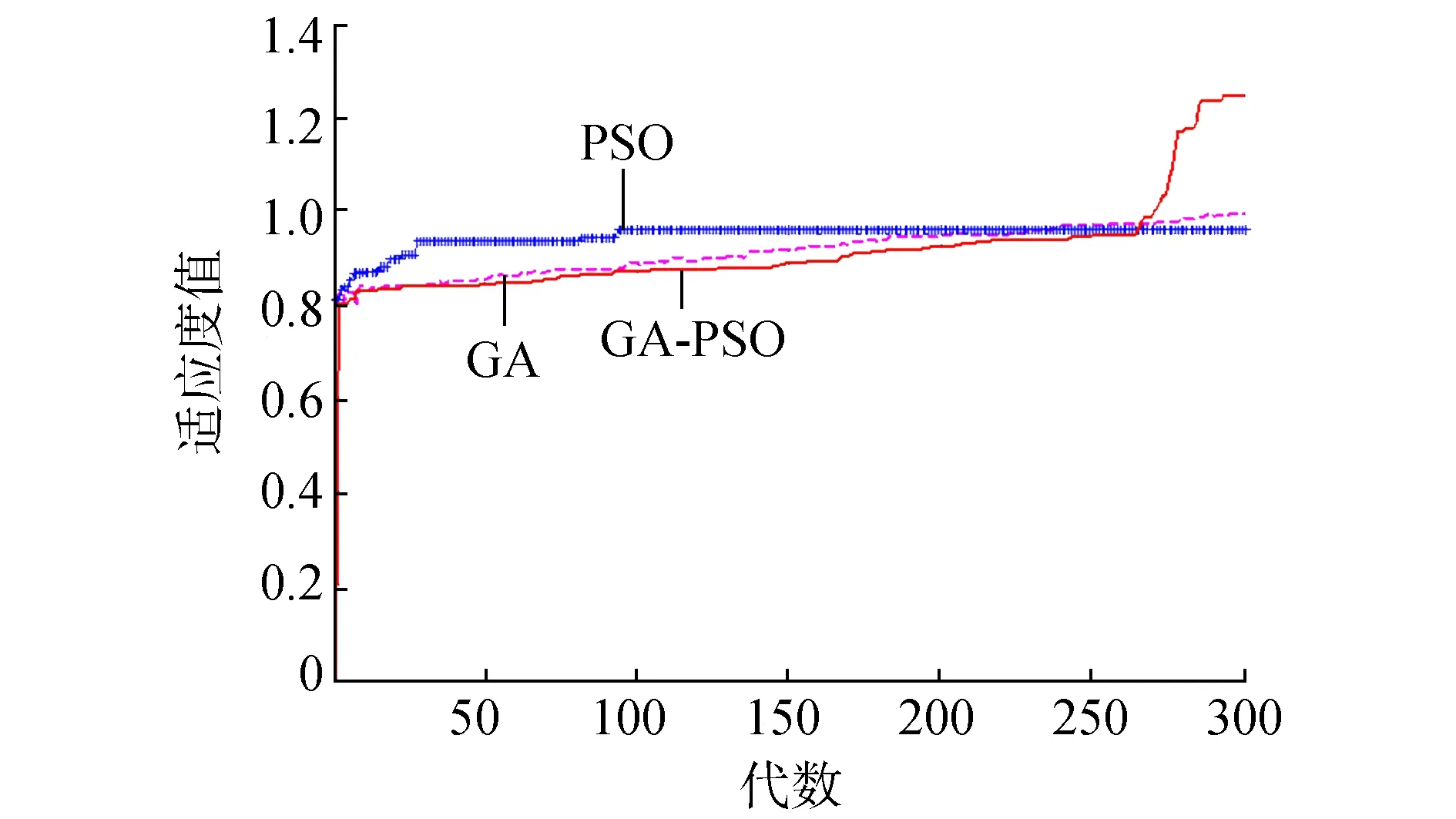
数据集D中含有k个样本D={x1,x2,…,xk},并且D中的每个样本都有特征集合F,F包含n维特征,xi∈Rn。对于分类问题,可将D中样本划分为目标向量C中的m个不同的类C={C1,C2,…,Cm}。特征选择的目的,是在原始特征集合N中寻找到一个最佳特征子集P,其中含有p维特征(p 特征选择处理包括4个组件:特征子集生成、子集评估、终止条件和结果验证。如图1所示,在阶段1中根据一个确定的搜索策略特征子集生成组件会预先产生候选特征子集。每一个候选特征子集都会被一个确定的评估方式所度量,并与之前最佳的候选特征子集做比较,如果新的特征子集表现得更加优越,那么替换原有的最佳特征子集。当满足设定的终止条件时,生成和评估这两个过程将不再循环。在阶段2中,最终所选的特征子集需要被一些给定的学习算法进行结果验证,其中ACC为学习正确率[3]。 图1 特征选择处理的统一视角Fig.1 A unified view of feature selection process 1.2 遗传算法基本原理 遗传算法作为一种自适应全局优化搜索算法,其选择、交叉与变异的3个算子成为种群寻优和保持解多样性的关键。其基本执行过程如下。 1) 初始化:确定种群规模N、交叉概率Pcross、变异概率Pmutation和终止进化准则。 2) 个体评价:计算每个个体的适应度。 3) 种群进化: ①选择算子:个体被选中的概率与其适应度函数值成正比。 ②交叉算子:根据交叉概率Pcross对2条染色体交换部分基因,构造下一代新的染色体。 ③变异算子:根据概率Pmutation对群体中的不同个体指定的基因位进行改造。 ④终止检验:如已满足终止准则,则输出最优解;否则转到2)。 1.3 二元粒子群优化基本原理 粒子群优化算法,源于对鸟群捕食的行为研究,是由Kennedy和Eberhart等[13]开发的一种新的进化算法。粒子在搜索空间内寻优,并定位当前路径中的最佳位置。每一个粒子都需要考虑自身当前的位置和速度,记录它们自己的最优解(最佳位置)pbset,并根据粒子群体内全局最优解gbest调整当前自身位置,粒子的具体更新如下: 基于上述研究,学者Kennedy调整了连续PSO方法中速度和位置的更新方式,提出了适用于解决离散问题的二元粒子群算法(binary particle swarm optimization,BPSO)[14]。该思想中的粒子仅可以在二元空间中进行搜索,粒子的位置向量仅可以用0或1表示。BPSO方法中影响其寻优能力的关键之一就是转换函数,利用该函数将连续的速度值转化为离散的位置。在最初的研究中使用式(3)中的sigmoid函数作为转换函数将实值的速度映射为[0,1]之间的值。 2.1 编码方式 本文使用了二进制比特串的编码方式,该编码方式通用于遗传算法和二元粒子群方法,如图2所示。将每个二进制串作为一个个体(粒子),个体(粒子)中的每一维(每一比特)都代表一个候选特征,当该位为1时表示该特征被选中,并添加到候选的特征子集中;当该位为0时表示该特征未被选中。依据此编码方式将特征选择问题转换为寻找最佳个体(粒子)的问题。 图2 二元粒子群的编码方式Fig.2 Coding scheme of BPSO 2.2 适应度函数 本文使用互信息熵理论对特征子集进行整体评估,两个变量的互信息值越大,则意味着两个变量相关程度越紧密;当互信息为零时,则意味着两个变量完全不相关。特征集合F={f1,f2,…,fn}中某一特征fi与类别的互信息度量如下: 式中:H为变量的熵值,用以度量随机变量信息的不确定性。以类别向量为例,H(C)通常用作描述离散随机变量C={c1,c2,…,cn}熵值,ci是变量C的可能取值,p(ci)为概率密度函数。 当已知特征变量和类别变量fi和C的联合概率密度时(对于离散数据意味着两个变量对应的属性值联合出现的频度),两者的联合熵为 基于特征与类别向量的信息熵度量构建适应度函数,适应度函数的度量体现了进化过程对优良个体的保留,对低劣个体的淘汰。本文在设计适应度函数时不仅考虑了特征与类别的相关性,而且将特征子集规模也作为影响个体(粒子)适应度的一部分,适应度函数的设计试图找出子集规模小,并且特征与类别高度相关的特征集合。具体适应度函数设计如下: 式中:MI部分为特征与类别关联性度量;S部分为特征子集规模控制。假设当前候选特征子集为在全部n维特征中选出的p维特征: 本文设计式(8)和式(9)两个适应度函数,在寻优过程中试图寻找最大值。其原理在于,小规模数据集特征维度较少,在进化过程中对特征空间搜索较为全面。采用式(8)重点考察特征与类别的相关性。而对于大规模数据集,特征维度较大,进化搜索特征空间的过程中很难控制特征子集规模,并且容易在候选特征较多时形成局部最优,所以在式(9)中增大了对特征子集规模的惩罚系数。假设式(8)和式(9)获得相同的适应度函数值,式(9)需要尽量减小k值,使得选择特征尽量少以取得关联性度量和子集规模的平衡。 2.3 比特率交叉算子 在遗传算法中,交叉算子通过模拟自然界生物的杂交过程对个体进行交叉操作,不断产生新个体、增加种群的多样性、扩大寻优范围,从而使得遗传算法具有较强的搜索能力。直观地讲,交叉算子影响了遗传算法对求解空间影响的搜索能力,并对能否找到全局最优解发挥了至关重要的作用[15]。 传统的GA算法交叉操作采用的是单点交叉,但是在该交叉操作中很可能出现“近亲繁殖”的现象,即进行交叉操作的一对个体基因型相似,减缓了遗传算法的搜索速度,或者会出现局部收敛或早熟收敛,从而影响种群的进化方向。因此本文针对特征选择问题提出了比特概率交叉算子,在基因交叉的过程中,首先判断两个个体的基因相似比特率,并将比特率与交叉概率作比较,若小于该概率则进行个体基因交叉操作。具体过程如算法1所示。 算法1 比特概率交叉算子 输入 两个个体的二进制比特基因信息位f(i,:)和f(j,:),染色体长度n,交叉概率Pcross。 输出 交叉后两个个体的基因型f(i,:)和f(j,:)。 1)m=0。 2)Fork=1:n。 3)若两个体的第k位比特位相同则m=m+1。 4)End For。 5)计算个体间基因型相似比s=m/n。 6)Ifs 7)随机选定基因型个体的某一位Poscross。 8)Forh=Poscross:n。 9)交换个体Poscross位到第n位的基因。 10)End For。 11)End If。 通过比特率交叉算子可以避免基因型相近的个体进行交叉操作,即可以避免产生“隐性致病基因”,防止相近个体的近亲繁殖,并增强种群个体的多样性。 2.4 GA-PSO协同演化方法的实现 本文提出的GA-PSO算法的主要思想是比特位信息交互。传统的PSO特征选择有一定的缺陷,比较容易陷入全局最优解并且过早收敛,进化过程中会将搜索引向本次迭代的全局和个体最佳位置,因此进化的多样性差。协同的思想对于PSO特征选择方法的帮助在于,通过本文提出的最佳个体比特信息位交换策略,每次进化产生最佳个体的比特信息位不仅仅由PSO决定,事实上它和GA中的最佳个体共享那些能够引起适应度值增加的优秀比特信息位。将这些优秀的比特基因随机地插入到粒子群中最佳个体对应的信息位上。这种方法不仅有可能使最佳个体变得更优秀,还为PSO算法增加了多样性,避免过早地陷入局部最优解。对于GA特征选择方法来说,寻优速度较慢,尤其在高维特征下往往不能获得令人满意的结果。从信息共享机制来说,遗传算法的信息共享方式主要是通过两个个体之间的交叉操作,而粒子群算法的信息共享方式是通过种群中的最优个体传递信息给其余个体。这两种信息共享机制就相应地决定了两种算法的表现,粒子群算法每代都选出当前最优个体,并进行全局范围的信息共享,使得整个粒子群能向着最优的方向快速趋近;而遗传算法的交叉操作具有一定的随机性,且由于是一对一进行交叉,每一次迭代中作用的范围相对较小,使得种群中的优秀基因交流较慢,整个种群的进化比较漫长,所以PSO特征选择寻优速度较快,效率更高。通过信息交互,在迭代过程中种群可以获得更为优秀的个体基因型,这有助于加速GA种群的进化过程,提高收敛速度。同时,通过上文的比特率交叉算子可以避免相近的基因型交叉产生不“健康”的后代个体。具体的GA-PSO协同演化算法如算法2和算法3所示。 算法2 协同演化算法 输入 粒子群和种群初始化参数。 输出 最佳个体。 1)初始化粒子群和种群。 2)协同演化。 ①计算各个粒子的适应度值。 ②选择粒子群算法最佳个体PSObest。 ③选出遗传算法最佳个体GAbest。 ④最佳个体比特信息位交换。 ⑤PSO:更新粒子速度及位置。 ⑥GA: 选择、比特率交叉(算法1)和变异。 3)判断终止条件,若不满足返回2),满足进入4)。 4)比较GAbest与PSObest,输出最佳个体。 算法3 最佳个体比特信息位交换 输入 上一代最佳个体和本轮最佳个体。 输出 交换比特信息位后的PSObest及HSbest。 1) 随机选取PSO中引起最佳个体适应度值增加的信息位PSObit。 2) 随机选取GA中引起最佳个体适应度值增加的信息位GAbit。 3) if PSObest优于 GAbest, 将GAbest中对应的信息位改为PSObit; else 将PSObest中对应的信息位改为GAbit; end 本文提出的GA-PSO协同演化算法,通过协同共享的思想让PSO和GA互相弥补各自的弱点,互相协助从而产生更强的个体。对于本文面向的特征选择问题,更好的个体可以从两个角度进行判断:特征与类别相关性越高,个体适应度值越高;特征子集规模越小,个体适应度值越高。面向特征选择问题的协同演化方法执行流程如图3所示。 图3 协同演化算法的流程图Fig.3 Flow chart of co-evolution algorithm 为了验证本文提出算法的有效性,实验结果从两个方面进行分析:1)分析算法在不同数据集下分类的准确率;2)提出的算法与GA和PSO进行适应度值和收敛性比较。本文实验特征选择部分的运行环境为MATLAB 2014a,分类准确率运行环境为weka3.8。对数据的离散化处理采用经典的MDL方法。种群规模为20,迭代次数为300。GA中交叉概率为0.6,变异概率为0.15;PSO中c1=c2=2,w=0.4。 3.1 算法分类准确率的结果分析 本文实验部分选用了UCI(UC Irvine machine learning repository)数据库中的5个高维多类别数据集,特征维度从14维升至240维,不同数据集中样本的类别数目最少为2类,最多为10类。其中,Australian与Credit Approval为两个信用卡申请类数据集,Dermatology为皮肤病数据集,Synthetic Control是名为合成控制图数据集,Multi-Feature Pixel是名为Multi-feature “0”到“9” 手写图数据集中的一个子集合。各数据集的详细信息如表1所示。 表1 UCI数据集描述 实验对比的特征选择算法有GA、PSO、IG以及GR。为了验证算法性能,选取SVM、1-NN和Naïve Bayes 三个分类器,并且使用十折交叉验证的方法测试在不同数据集下各个算法所选择特征子集的分类。对于GA,PSO和GA-PSO三种进化搜索的方法,实验得出每个算法连续运行20次时的平均分类准确率。而IG(information gain)信息增益和GR(gain ratio)增益比率都是以互信息为基础的经典的排序特征选择算法,因此在实验中分别对每个数据集的特征进行排序,并且手动地选择与进化算法规模相近的排名前p个特征,p为选择的特征数量。具体的分类结果如表2~4所示。表2~4中数值表示各特征选择算法选择的特征子集在相应的数据集下使用分类器得到的分类准确率。Avg表示平均分类准确率,括号内数字为平均选择的子集规模。 从表2中可以看出,本文提出的方法在5个数据集上均取得了最好的结果,比如在Synthetic Control数据集中,在选出相近的特征子集下,提出的方法的平均分类准确率比其他算法的平均分类准确率高出了平均2.98%。同样如表3和表4所示,在1-NN和Naïve Bayes分类器中,对于每个数据集本文提出的方法的平均分类准确率都比其他的算法具有优势,在保证特征子集近似的情况下,能够得到较好的分类效果。 表2 1-NN分类器的分类准确率 表3 SVM分类器的分类准确率 表4 Naïve Bayes分类器的分类准确率 综合GA-PSO在SVM、KNN和Naïve Bayes 三个分类器下的表现,本实验结果验证了GA-PSO算法在不同规模数据集下分类性能的有效性,从分类准确率的角度评定本文提出的GA-PSO算法优于传统的GA和PSO进化算法,也优于经典的特征选择排序算法,平均分类精度有明显提升。 3.2 算法适应度值的分析 在进化算法中,对于求最大化的目标函数而言,适应度值高的个体能够在最大的程度上得到保留。适应度值高的个体的基因型对种群的进化方向起着指导作用。因此对于不同的演化方法,另一个评定的角度是在同一个适应度函数作用下比较哪种算法能够得到更高的适应度值的个体。为了分析比较提出算法在进化过程中适应度值的变化情况,分别画出了GA-PSO、GA和PSO算法在Synthetic Control、Dermatology和Multi-Feature Pixel数据集下单次迭代过程中适应度函数值的折线图,如图4~6所示。 图4 Dermatology 数据集中的对比Fig.4 Comparison on Dermatology 图5 Synthetic Control数据集中的对比Fig.5 Comparison on Synthetic Control 图6 Multi-Feature Pixel数据集中的对比Fig.6 Comparison on Multi-Feature Pixel 对适应度值的分析:通过图4可以看出,在0~150代GA-PSO保持着GA近似水平的适应度值,PSO的适应度值稍高,在150代以后GA-PSO和GA适应度值逐步提升,超过PSO,最终GA-PSO得到最高的适应度值;在图5中,在240代后GA-PSO超过GA和PSO,最终GA-PSO取得最高的适应度值;在图6的超高维数据集中,GA-PSO的寻优优势更加明显。GA-PSO比传统的进化算法PSO和GA具有更强的搜索能力,在相同条件下总是能保持进化以找到更优的个体。 对收敛性的分析:随着特征规模的增大,PSO总是过早收敛,这说明PSO算法容易陷入局部最优解,尤其对于高维特征数目的数据集,PSO不能保证良好的全局搜索;GA的全局搜索能力要优于PSO;GA-PSO则一直保持着良好的搜索能力,尤其在大规模数据集中,GA-PSO的表现更为突出,在300代以内,适应度值一直保持着提升,能够有效地避免陷入全局最优解。 综上所述,本文所提出的算法在进化过程中能够产生比较优秀的个体,获得比较高的适应度值,从而可以取得更好的分类准确率。这证明了,GA-PSO算法在进化过程中逐步寻优的能力,能够找出相对优秀的特征子集。 本文提出了面向特征选择问题的协同演化算法GA-PSO。为了保证种群多样性,提出了一种基于比特率的交叉算子。针对GA和PSO寻优的不同特点进行共同演化,并将影响最佳个体形成的比特基因位作为公共信息实现共享。通过实验对比验证了协同演化的方法要优于单一进化的方法,并且验证了全局搜索的特征选择方法优于传统的贪婪式特征选择方法。本文的研究不仅可以有效地解决特征选择问题,在其他的组合优化离散问题中也可以使用该思路进行协同演化。未来将进一步研究子集规模的自适应控制以及其他适应度评价方法。 [1]DASH M, LIU H. Feature selection for classification[J]. Intelligent data analysis, 1997, 1(1/2/3/4): 131-156. [2]GUYON I, ELISSEEFF A. An introduction to variable and feature selection[J]. The journal of machine learning research, 2002, 3(6): 1157-1182. [3]ZHAO Zheng, MORSTATTER F, SHARMA S, et al. Advancing feature selection research. ASU feature selection repository[R]. Phoenix: School of Computing, Informatics, and Decision Systems Engineering, Arizona State University, Tempe, 2010. [4]BATTITI R. Using mutual information for selecting features in supervised neural net learning[J]. IEEE transactions on neural networks, 1994, 5(4): 537-550. [5]YANG Yiming, PEDEREN J O. A comparative study on feature selection in text categorization[C]//Proceedings of the 14th International Conference on Machine Learning. San Francisco, CA, USA 1997: 412-420. [6]周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 247-266. [7]XUE Bing, ZHANG Mengjie, BROWNE W N, et al. A survey on evolutionary computation approaches to feature selection[J]. IEEE transactions on evolutionary computation, 2016, 20(4): 606-626. [8]PENG Hanchuan, LONG Fuhui, DING C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(8): 1226-1238. [9]UNLER A, MURAT A, CHINNAM R B. Mr2PSO: a maximum relevance minimum redundancy feature selection method based on swarm intelligence for support vector machine classification[J]. Information sciences, 2011, 181(20): 4625-4641. [10]CERVANTE L, XUE Bing, ZHANG Mengjie, et al. Binary particle swarm optimisation for feature selection: a filter based approach[C]//Proceedings of 2012 IEEE Congress on Evolutionary Computation. Piscataway. Brisbane, Australia, 2012: 1-8. [11]DONG Hongbin, TENG Xuyang, ZHOU Yang, et al. Feature subset selection using dynamic mixed strategy[C]// Proceedings of 2015 IEEE Congress on Evolutionary Computation. Sendai, Japan, 2015: 672-679. [12]NEMATI S, BASIRI M E, GHASEM-AGHAEE N, et al. A novel ACO-GA hybrid algorithm for feature selection in protein function prediction[J]. Expert systems with applications, 2009, 36(10): 12086-12094. [13]KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of 1995 IEEE International Conference on Neural Networks. Perth, Australia, 1995: 1942-1948. [14]KENNEDY J, EBERHART R. A discrete binary version of the particle swarm algorithm[C]//Proceedings of 1997 IEEE International Systems, Man, and Cybernetics. Orlando, USA, 1997: 4104-4108. [15]李书全, 孙雪, 孙德辉, 等. 遗传算法中的交叉算子的述评[J]. 计算机工程与应用, 2012, 48(1): 36-39. LI Shuquan, SUN Xue, SUN Dehui, et al. Summary of crossover operator of genetic algorithm[J]. Computer engineering and applications, 2012, 48(1): 36-39. Co-evolutionary algorithm for feature selection TENG Xuyang, DONG Hongbin, SUN Jing (College of Computer Science and Technology, Harbin Engineering University, Harbin 150001, China) Feature selection is a key preprocessing technology of machine learning and data mining. The traditional greed type of feature selection methods only considers the best feature of the current round, thereby leading to the feature subset that is only locally optimal. Realizing an optimal or nearly optimal feature set is difficult. Evolutionary search means can effectively search for a feature space, but different evolutionary algorithms have their own limitations in search processes. The evolutionary advantages of genetic algorithms (GA) and particle swarm optimization (PSO) are absorbed in this study. The final feature subset is obtained by co-evolution, with the information entropy measure as an assessment function. A specific bit rate cross operator and an information exchange strategy applicable for a feature selection problem are proposed. The experimental results show that the co-evolutionary method (GA-PSO) is superior to the single evolutionary search method in the search ability of the feature subsets and classification learning. In conclusion, the ability of combined evaluation, which is provided by an evolutionary search, is better than that of the traditional greedy feature selection method. feature selection; genetic algorithm (GA); particle swarm optimization (PSO); co-evolution; bit rate cross 滕旭阳,男,1987年生,博士研究生,主要研究方向为机器学习、智能优化算法。 董红斌,男,1963年生,教授,博士生导师,主要研究方向为多智能体系统、机器学习。 孙静,女,1993年生,硕士研究生,主要研究方向为机器学习、数据挖掘。 10.1992/tis.201611029 http://kns.cnki.net/kcms/detail/23.1538.TP.20170302.1522.002.html 2016-11-19. 日期:2017-03-02. 国家自然科学基金项目(61472095,61502116);黑龙江省教育厅智能教育与信息工程重点实验室开放基金项目. 孙静. E-mail:sunjing@hrbeu.edu.cn. TP301 A 1673-4785(2017)01-0024-08 滕旭阳,董红斌,孙静.面向特征选择问题的协同演化方法[J]. 智能系统学报, 2017, 12(1): 24-31. 英文引用格式:TENG Xuyang,DONG Hongbin,SUN Jing.Co-evolutionary algorithm for feature selection[J]. CAAI transactions on intelligent systems, 2017, 12(1): 24-31.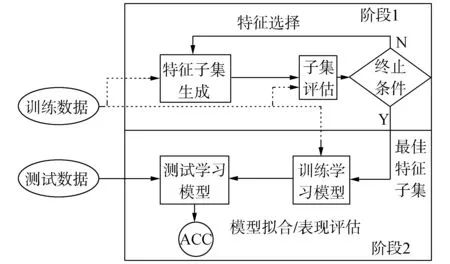
2 求解特征子集的协同演化方法

3 实验结果与分析
4 结束语



