基于纠错码的指静脉加密算法

王科俊，曹逸，姜博威，徐怡博,邢向磊

(哈尔滨工程大学 自动化学院 黑龙江 哈尔滨 150001)

基于纠错码的指静脉加密算法

王科俊，曹逸，姜博威，徐怡博,邢向磊

(哈尔滨工程大学 自动化学院 黑龙江 哈尔滨 150001)

对指静脉加密算法进行整体介绍，并加入纠错机制，设计了带纠错功能的指静脉加密算法。利用二进制序列发生器随机生成一个多项式系数形式的密钥，将指静脉特征点加密，在密钥恢复阶段用拉格朗日插值来恢复多项式，并利用循环冗余校验码进行校验，该方法可以找到最精确的密钥来保证多项式的准确度。实验结果表明：利用带有纠错码的模糊金库算法很好地实现了指静脉模板的加密和解密，从而达到了保护生物信息安全的要求；通过密钥长度增长可以提高系统的安全性能。

指静脉加密；纠错码；指静脉特征点；生物加密；随机密钥；模糊金库算法

生物识别技术已经取代传统的密码或ID卡，成为一项方便可靠的验证人身份的技术[1]。作为人的身体特征，生物特征(指纹、虹膜、静脉等)不会被遗忘或丢失，而且很难被伪造[2-3]。一般的生物特征识别方法是从原始样本中提取出生物特征模板并存储于模板库中用于匹配和比对。

因为生物特征不能像密码或ID卡一样被更换或复位，因此可能会带来严重的安全和隐私问题[4]。一个人的生物特征有限，如果被他人别有用心地窃取到，那么生物特征模板也就会被窃取到，这将会带来严重的后果。生物特征加密系统的提出解决了上述问题[5]。生物特征加密系统使用加密技术或其他特定的技术在加密域生成生物特征加密模板，然后将加密模板存储到数据库中[6]。这样的加密过程是不可逆的，即原本的生物特征不能直接从加密模板中得到[7]。

相比于指纹[8]、手形[9]、掌纹[10]等手部特征，采用手指静脉特征进行加密具有独特的优越性。在加密时，采用了Fuzzy Vault(模糊保险箱)方案[11]。首先，用指静脉的特征模板编码密钥；然后，再处理指静脉的特征模板，将模板以点对的形式混杂在大量的干扰数据中。攻击者很难从混杂的大量数据中提取出真实的指静脉特征，这样便起到了加密的作用。只有拥有真实样本的解密者才能成功解密，得到密钥。

为了更加精确地完成加密和解密生物模板的功能，我们采用带有循环冗余检验码的指静脉密钥绑定算法。这种算法能够降低错误匹配指静脉的概率，同时能提高加密的准确性，降低加密信息被攻击者破解的概率。

1 循环冗余校验码(CRC)算法及分析

1.1 CRC算法的定义

CRC利用n维实多项式线性空间进行编码[12-13]。任意要处理的二进制数据都可以写成一个n阶的实多项式：

例如，11001110这个二进制数，在实多项式线性空间的表示为

1x7+1x6+0x5+0x4+1x3+1x2+1x1+0

采用CRC算法时，发送方和接收方利用同一个二进制在多项式线性空间进行表示。需要使多项式的最高阶元素和最低阶元素的系数同时为1。在校验时，若数据帧无错误地传输，则校验结果应为零。

CRC校验可以检测出所有奇数个随机的错误和长度小于多项式阶数的错误。因此，为了降低误判的概率，可以采用更高阶次的生成多项式。例如，使用CRC-16算法，即采用16 bit的CRC校验可以保证1 014 bit的码元中仅有一个未被检测出错误。它的生成多项式为

1.2 CRC校验码的算法分析

CRC校验码的编码过程为：首先将要发送的二进制数在多项式线性空间线性表示为g(x)，然后除以xyt(x)生成多项式，最后取余数y(x)作为CRC校验码。具体步骤如下：

将待发送的m位二进制数在多项式线性空间表示为t(x)，设生成多项式g(x)为r阶多项式，在待发送数据的末尾添加r个0，使多项式长度变为m+r位，则待发送数据构成的新多项式为xyt(x)。

生成多项式g(x)除以多项式xyt(x)，取余数得到一个r-1阶次的多项式y(x)，即为t(x)的校验码。

待发送数据构造的新多项式xyt(x)除以2取模再减去y(x)，得到xrt′(x)。xrt′(x)系数就是经过CRC编码的待发送二进制数据。可以看出，经过CRC编码后待发送的数据构成的任意多项式t(x)被构造成了可以被g(x)除尽的多项式xrt′(x)。解码时只需要用接收到的数据生成多项式，并且除以生成多项式g(x)，若能整除则证明传输的数据正确，反之则有误。同时，由构造xrt′(x)的方法可知，在解码得到多项式xrt′(x)之后，只需要去掉数据尾部的r位二进制数，即可还原加密的数据。

2 基于纠错码的指纹加密算法模糊金库的实现

2.1 指静脉图像预处理

在各种外界因素(例如光线变化等)的影响下，采集到的指静脉图像是含有大量噪声的灰度图像。噪声的存在严重干扰了指静脉识别的准确性。所以在识别指静脉图像之前，要对图像做滤波等处理，使图像变得清晰易识别，便于提取指静脉特征。

指静脉图像的预处理过程一般包括归一化、方向滤波、图像增强、细化等部分。所以在指静脉特征点提取之前做了必要的图像预处理。文中参考其他文献对指静脉预处理的方法[14-15]，在提取指静脉图像时采用了区域合并和分水岭的算法。在经过预处理后，提取指静脉图像上的交叉点作为特征点，如图1所示。

图1 指静脉图像预处理与特征点提取Fig.1 Finger vain image preprocessing and feature point extraction

2.2 基于纠错码的指静脉加密算法流程图(如图2)

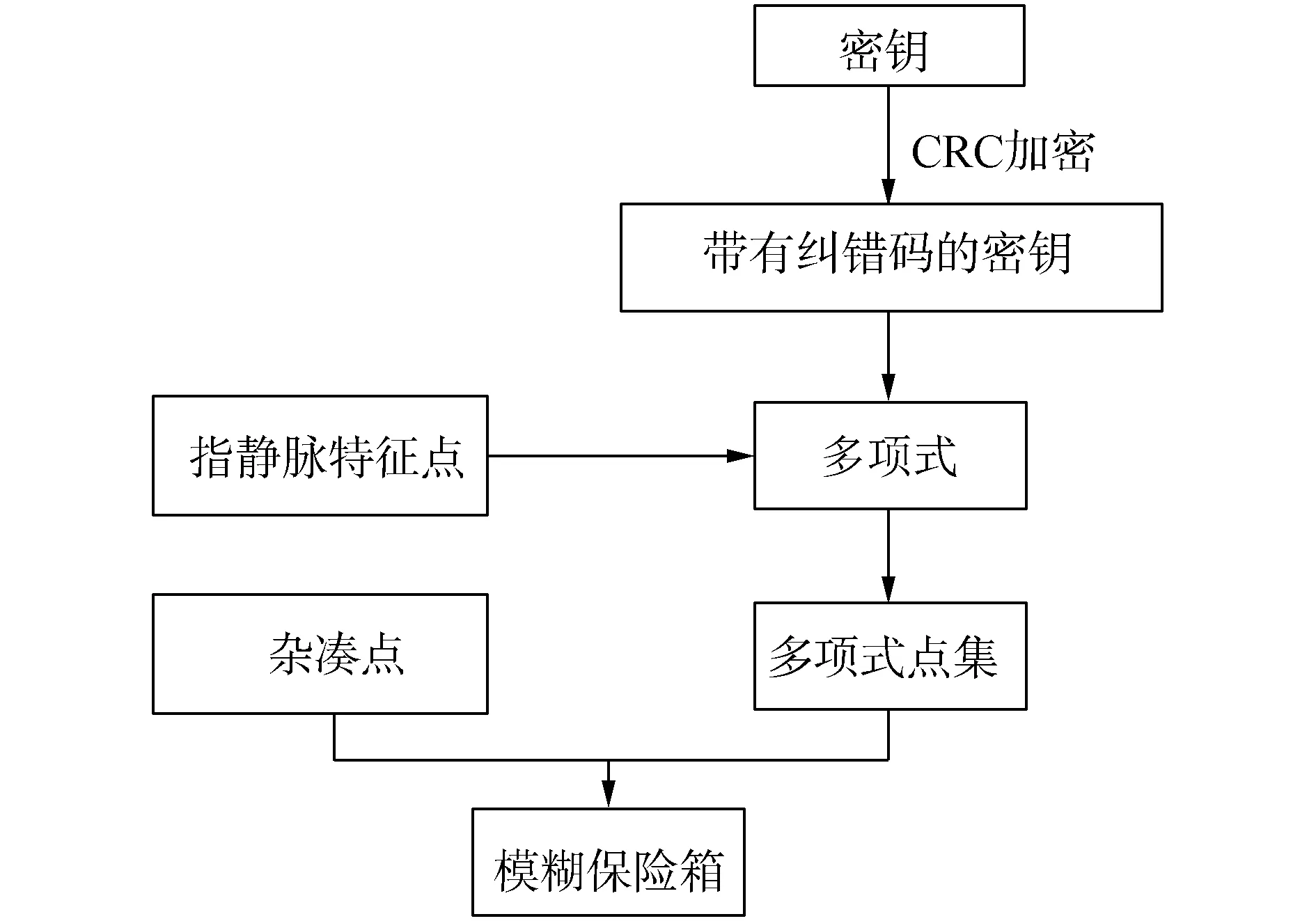
图2 加密流程图Fig.2 The flow chart of encryption

2.3 基于纠错码的指静脉加密实现方法

在实际应用中受各种条件影响，一幅指静脉图像可提取出的指静脉特征点数量是随机的。但是，特征点个数n需要考虑密钥长度的问题。若n的取值过小，则密钥的准确性和安全性均会下降。因此，为保证运算域足够大，以及考虑到解密的准确性和保险箱的安全性，运算选择在有限域GF(216)中进行。

节点用平面坐标系中的坐标来表示，用M表示指静脉特征点坐标集合，即

式中：li1、li2是第i个指静脉特征点分别到相邻两特征点距离的最大值；θi是两个距离之间的夹角；Ng是指静脉特征点的总数。因为

将ui转换成16 bit的二进制串作为加密单元，从而形成特征点集合，即

用m序列发生器产生192 bit的随机二进制数作为密钥，并在多项式线性空间中表示为[16]

式中：a12到a1是将192 bit的二进制数串平分为12个长度为16 bit的二进制串；a0是由CRC-16算法产生的，用来进行解码校验。将所有的ui代入p(u)中，所有的结果构成的集合为

为了保证特征点安全加入杂凑点集合，集合定义为

式中：Nc是杂凑点集合中杂凑点的数量。杂凑点(xi,yi)不满足多项式p(u)，即yi≠p(xi)，∀i=1,2,…,Nc。如图3所示，将杂凑点集合与特征点集合无序地混合在一起就形成了保险箱，即

式中Nc≫Ng，这样可以增加攻击者破译的难度和提高密钥的安全性。

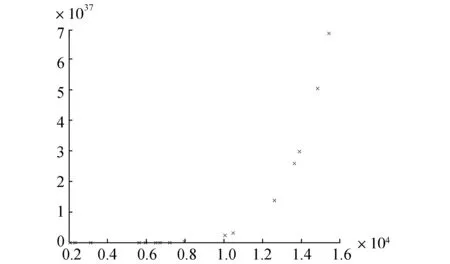
(a) 真实点集合

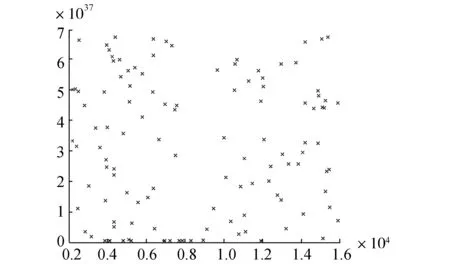
(b)特征点和杂凑点的集合图3 特征点和杂凑点的集合Fig.3 The formation of Fuzzy vault

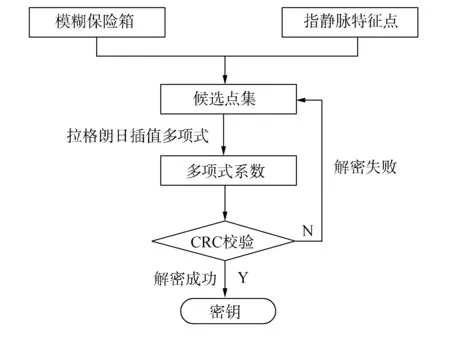
图4 解密流程图Fig.4 The flow chart of decryption

2.4 密钥恢复

密钥恢复阶段，解密流程如图4所示，首先提供指静脉模板和保险箱，由系统预处理，从指静脉模板中提取出用于查询指静脉特征点的集合：

Q={(l1q0,l2q0,θ0),(l1q1,l2q1,θ1),…,(l1qN*,l2qN*,θN*)}

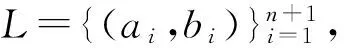
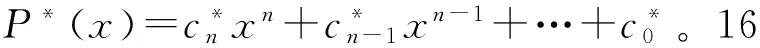
假设在加入杂凑点之后，指静脉有r个点，t个特征点，生成多项式的阶数为k-1。则暴力破解密钥和合法拿到密钥的复杂性比值为

非合法用户想要获得密钥的难度将会非常大。在理论上对密钥的保护是可以达到非常好的效果的，只有合法用户使用正确的模板才能获得正确的密钥。

3 实验结果分析与讨论

若想增加加密的安全性，则需要增加杂凑点M的数目，M越大，攻击者需要尝试的次数就越多。但同时，由于平面坐标区域有限，并且杂凑点和真实点之间要保持一定距离，限制了杂凑点M的个数。一般来说，杂凑点的数目取200～500。

在哈尔滨工程大学自动化学院的手指静脉库中，选取300幅图像大小为320×240像素的食指静脉图像作为指静脉图像训练库，用于加密。将这300人每人另采集4幅共1 200幅食指图像，组成验证库，用于解密。在点的选择方面，选取真实点16个，多项式阶数为7～12，杂凑点个数为200个。实验结果如表1和表2所示。

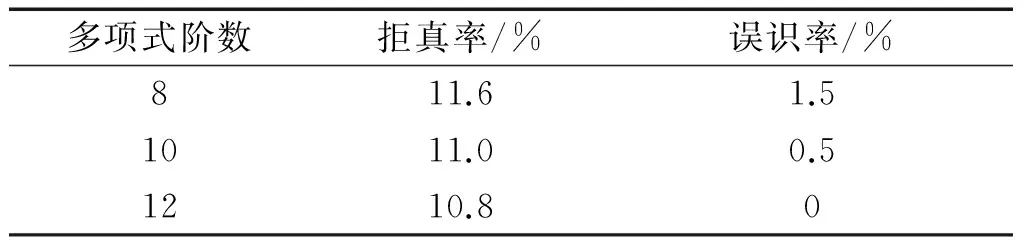
表1 不同多项式阶数下的拒真率(FRR)和误识率(FAR)

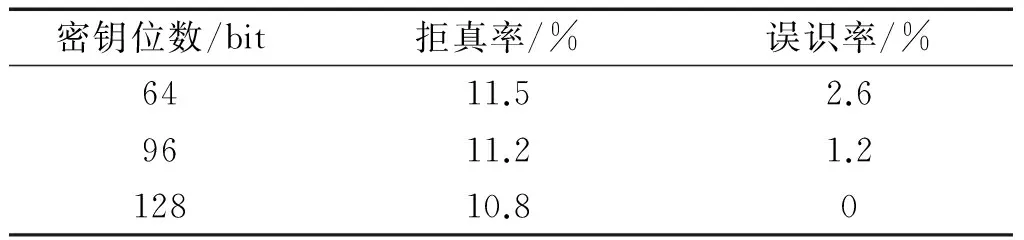
表2 不同密钥位数下的拒真率(FRR)和误识率(FAR)

从表1中可以得到，FRR和FAR随着多项式阶数的增加而下降，当多项式阶数为12时，误识率为0。

从表2中可以得到，FRR和FAR随着密钥长度的增加而下降，当密钥长度为128 bit时，误识率为0。

从实验结果来看，本文加密算法的拒真率略高，但在可接受范围内，而误识率很低，说明此算法安全性很高，能够很好地防止非法者获取密钥。

通过实验证明，模糊保险箱算法能够确保模板的安全，并且随着多项式阶数的增加，识别指静脉的错误率也在降低。为防止多项式次数的增加导致对指静脉图像质量要求高而产生错误，在算法中引入了CRC码用来纠错，从而保证了系统的鲁棒性，实现了容错模糊保险箱算法。

5 结束语

本文介绍了模糊保险箱(fuzzy vault)算法，研究了基于纠错码的指静脉加密算法。首先，对采集到的指静脉图像进行预处理，使含有大量噪声的图像尽量清晰，易于提取特征；然后，用循环冗余检验码对指静脉模板进行加密和解密，在MATLAB中通过仿真验证了算法的可靠性；最后，利用实际实验，给出了多项式阶数和密钥长度对误识率和拒真率的影响，方便针对不同的性能选取多项式和密钥的长度。

虽然通过模糊保险箱算法得到的结果符合要求，但该算法仍然有很多需要改进的地方：图像预处理技术需要进一步提高，以改善得到指静脉图像的清晰度；特征点提取和杂凑点的生成有待改善，使提取到的特征点尽量准确，使杂凑点远离真实点的同时防止真实点被提取；该算法对提取到的指静脉图像质量要求较高，并且该算法时间复杂度也很高；实验还存在少量的指静脉图像由于质量问题导致特征点提取不合格从而造成最后的解密失败的问题；另外，实验中的拒真率虽然在可接受的范围内，但是仍然略高，导致解密的复杂度偏高。以上提出的问题也是下一步需要研究并改进的地方。

[1]戚文静，张素，于承新，等.几种身份认证技术的比较及其发展方向[J]. 山东建筑工程学院学报, 2004, 19(2): 84-87. QI Wenjing, ZHANG Su, YU Chengxin, et al. Developing trend comparison of several authentication techniques[J]. Journal of Shandong university of architecture and engineering, 2004, 19(2): 84-87.

[2]JAIN A, FLYNN P, ROSS A A. Handbook of biometrics[M]. US: Springer, 2008.

[3]符艳军, 程咏梅, 董淑福, 等. 结合人脸特征和密码技术的网络身份认证系统[J]. 计算机应用研究, 2010, 27(2): 737-739. FU Yanjun, CHENG Yongmei, DONG Shufu, et al. Authentication system based on combination[J]. Application research of computers, 2010, 27(2): 737-739.

[4]RATHA N K, CONNELL J H, BOLLE R M. An analysis of minutiae matching strength[M]//BIGUN J, SMERALDI F. Audio-and Video-Based Biometric Person Authentication. Berlin Heidelberg: Springer, 2001: 223-228.

[5]JAIN A K, NANDAKUMAR K, NAGAR A. Biometric template security[J]. EURASIP journal on advances in signal processing, 2008, 2008: 579416.

[6]CHUNG Y, MOON D, LEE S, et al. Automatic alignment of fingerprint features for fuzzy fingerprint vault[M]//FENG Dengguo, LIN Dongdai, YUNG M. Information Security and Cryptology. Berlin Heidelberg: Springer, 2005: 358-369.

[7]ULUDAG U, PANKANTI S, PRABHAKAR S, et al. Biometric cryptosystems: issues and challenges[J]. Proceedings of the IEEE, 2004, 92(6): 948-960.

[8]PERALTA D, TRIGUERO I, SANCHEZ-REILLO R, et al. Fast fingerprint identification for large databases[J]. Pattern recognition, 2014, 47(2): 588-602.

[9]CHAUDHARY D R, SHARMA A. Hand geometry based recognition system[C]//Proceedings of 2012 Nirma University International Conference on Engineering. Ahmedabad, India, 2012: 1-5.

[10]ZHANG D, ZUO Wangmeng, YUE Feng. A comparative study of palmprint recognition algorithms[J]. ACM computing surveys (CSUR), 2012, 44(1): 2.

[11]JUELS A, SUDAN M. A fuzzy vault scheme[C]//Proceedings of 2002 International Symposium on Information Theory. Lausanne, Switzerland, 2002: 408.

[12]张平安. 16位循环冗余校验码(CRC)的原理和性能分析[J]. 山西科技, 2005(5): 123-125. ZHANG Ping’an. An analysis of the principle and performance of 16-bit circulation redundancy check (CRC)[J]. Shanxi science and technology, 2005(5): 123-125.

[13]YANG Bian, CHU Huiguang, LI Guoqiang, et al. Cloud password manager using privacy-preserved biometrics[C]//Proceedings of 2014 IEEE International Conference on Cloud Engineering. Boston, USA, 2014: 505-509.

[14]熊新炎, 王科俊, 贲岘烨, 等. 一种新的近红外手背静脉模式骨架提取方法[J]. 哈尔滨工业大学学报, 2008, 40(1): 147-150. XIONG Xinyan, WANG Kejun, BEN Xianye, et al. A new method of near-infrared hand vein pattern skeleton extraction[J]. Journal of Harbin institute of technology, 2008, 40(1): 147-150.

[15]王科俊, 丁宇航, 王大振. 基于静脉识别的身份认证方法研究[J]. 科技导报, 2005, 23(1): 35-37. WANG Kejun, DING Yuhang, WANG Dazhen. A study of hand vein-based identity authentication method[J]. Science & technology review, 2005, 23(1): 35-37.

[16]ULUDAG U, PANKANTI S, JAIN A K. Fuzzy vault for fingerprints[C]//KANADE T, JAIN A, RATHA N K. Audio-and Video-Based Biometric Person Authentication. Berlin Heidelberg: Springer, 2005: 310-319.

[17]冯全, 苏菲, 蔡安妮. 一种利用多元线性函数绑定指纹细节点与密钥的新方法[J]. 兰州大学学报: 自然科学版, 2008, 44(2): 137-141. FENG Quan, SU Fei, CAI Anni. A new method for binding minutiae and cryptographic key using a multivariable linear function[J]. Journal of Lanzhou university: natural sciences, 2008, 44(2): 137-141.

[18]冯全, 苏菲, 蔡安妮. GRS解码在Fuzzy Vault中应用[J]. 计算机工程与应用, 2008, 44(13): 114-116. FENG Quan, SU Fei, CAI Anni. Application of GRS decoding in fuzzy vault[J]. Computer engineering and applications, 2008, 44(13): 114-116.

[19]NANDAKUMA K, JAIN A K, PANKANT S. Fingerprint-based fuzzy vault: implementation and performance[J]. IEEE transactions on information forensics and security, 2007, 2(4): 744-757.

Finger vain encryption algorithm based on an error-correcting code

WANG Kejun, CAO Yi ,JIANG Bowei, XU Yibo,XING Xianglei

(College of Automation,Harbin Engineering University, Harbin 150001,China)

This study presents an overall introduction of a finger vain encryption algorithm. A finger vain encryption algorithm with error correction is then designed by adding an error correction mechanism. This new finger vain encryption algorithm can produce a stochastic key in the form of a multinomial coefficient using a binary system sequencer, an encrypt finger vain, and the Lagrange interpolation value to restore the multinomial during authentication. The accuracy of this algorithm can be ensured using the cyclic redundancy check the code to determine the most accurate key. The experimental results indicate that the fuzzy vault algorithm with error correction can realize well the encryption and decryption of a vein template and meet the requirements of biological information security protection. In addition, the algorithm also indicates that the syste’s safety performance can be enhanced by changing the keys’ length.

finger vain encryption; error correcting code; finger vain minutiae; biometric encryption; random key; fuzzy vault algorithm

王科俊，男，1962年生，教授，博士生导师，学科带头人，主要研究方向为模糊混沌神经网络、自适应逆控制理论、可拓控制、网络智能控制、模式识别、多模态生物特征识别、联脱机指纹考试身份鉴别系统、微小型机器人系统。发表学术论文200余篇，出版学术专著3部，主审教材2部。

曹逸，女，1993年生，硕士研究生，主要研究方向为模式识别和生物特征识别。

邢向磊，男，1983年生，讲师，博士，主要研究方向为多集合度量学习和远离身份识别工作。

10.11992/tis.201609028

http://kns.cnki.net/kcms/detail/23.1538.TP.20170228.0832.002.html

2016-09-29.

日期：2017-02-28.

国家自然科学基金面上项目(61573114);黑龙江省自然科学基金面上项目(F2015033);中央高校基本科研基金项目 (HEUCF160415)

邢向磊. E-mail:xingxl@hrbeu.edu.cn.

TP391.41

A

1673-4785(2017)01-0055-05

王科俊，曹逸，姜博威,等.基于纠错码的指静脉加密算法[J]. 智能系统学报， 2017, 12(1): 55-59.

英文引用格式：WANG Kejun, CAO Yi, JIANG Bowei，et al. Finger vain encryption algorithm based on an error-correcting code[J]. CAAI transactions on intelligent systems, 2017, 12(1): 55-59.