面向旅游突发事件的客流量混合预测方法研究

陈 荣，梁昌勇，陆文星，董骏峰，葛立新

(1.蚌埠学院经济与管理学院，安徽 蚌埠 233000；2.合肥工业大学管理学院，安徽 合肥 230009；3.蚌埠学院理学院，安徽 蚌埠 233000)



面向旅游突发事件的客流量混合预测方法研究

陈 荣1，梁昌勇2，陆文星2，董骏峰2，葛立新3

(1.蚌埠学院经济与管理学院，安徽 蚌埠 233000；2.合肥工业大学管理学院，安徽 合肥 230009；3.蚌埠学院理学院，安徽 蚌埠 233000)

由于旅游突发事件的突然爆发性、危害性及信息不对称性，导致旅游客流量在短时间内发生急剧变化，原有模式被打破，非线性趋势和线性特征交织的随机性趋势明显，为旅游客流量正常预测带来极大的难度。本文提出一种面向旅游突发事件客流量混合预测方法，即支持向量回归(Support Vector Regression,SVR)和自回归求和移动平均模型(Autoregressive Integrated Moving Average, ARIMA)结合的混合预测方法：首先通过SVR预测旅游突发事件时期客流量，然后再用ARIMA预测SVR预测值的残差部分，最后将两者预测结果相加；同时针对客流量复杂特征，采用一种混沌粒子群算法(Chaos Particle swarm optimization, CPSO)实现对SVR参数选择。来自黄山风景区汶川地震时期客流量相关数据验证表明，混合预测模型优于单一预测方法，为旅游突发事件时期客流量预测提供了一种有效选择。

SVR；ARIMA；CPSO；旅游突发事件；客流量预测

1 引言

旅游业是一项对外界环境较敏感的行业，一些突发的旅游事件如自然灾害(地震、海啸、流行病等)和人为灾害(恐怖主义、政治动荡、战争等)等会对旅游行业造成极大的影响[1]。由于这些旅游突发事件通常发生突然、无法预料，社会影响大，信息不对称，会给景区造成极大的危害。它会使人们远离旅游目的地，破坏旅游系统发展天然而稳定的趋势和时间规律，从而使得景区管理者无法预知突发事件后客流量情况，给管理决策带来很大的不确定性。

旅游突发事件时期客流量作为旅游系统完整的一部分，通常被描述为“一种固有的非线性与线性相结合的复杂混沌动态系统”[2]。这种不同特征的混合，使得旅游突发事件时客流量较平常日和节假日更无规律性，现有单一预测方法难以实现这种非常规客流量预测[3]。故建立准确的能及时反映旅游突发事件时期客流量预测方法对旅游行业意义重大。

目前旅游突发事件客流量预测研究主要集中一些较大旅游突发事件的影响，如亚洲金融危机[4-5]、台湾大地震[6]、SARS[7-8]、911事件[9]等，所用方法主要以ARIMA、SARIMA、ARMAX和ADLM等单一方法为主，它们为旅游突发事件预测提供了一种相对有效的工具，但是它们只关注突发事件后旅游客流量长期趋势如月、季及年等预测，具体的短期的日客流量预测几乎没有涉及。组合预测方法[10-11]为处理线性与非线性等复杂预测提供了一种选择，但是该类方法是不同预测方法的线性组合，预测准确性受权重选取影响，目前对于权重的获取缺乏较为成熟的方法与理论指导，往往导致预测结果与实际值存在一定偏差。混合预测方法在处理非线性与线性相结合的预测问题上表现出良好的预测性能：将不同预测方法结合，充分利用各自方法的优点，它既克服单一方法技术上的弱点，又避免了组合预测方法权重选取的局限性，从而取得较单一方法和组合方法更好的预测性能和效果，增加了模型的适应性[12-13]。在混合预测方法中，以人工神经网络(Artificial neural network, ANN)为主的人工智能方法和以ARMA、ARIMA为基础的经典时间序列预测方法较为常用[14-16]，但是由于ANN方法自身存在局部最优及收敛速度慢等缺陷，且需要大量的数据进行训练，在现实中也往往难以实现准确预测。作为一种统计理论方法，SVR克服ANN方法上述缺点，具有很好的学习能力且善于捕捉到数据的非线性特征，因而在解决非线性、小样本问题上显示出很多独特的优点，而ARIMA模型是线性模型，非常适合线性趋势项的预测[17]。因此SVR与ARMA、ARIMA等结合混合预测是近年来发展起来的方法，在行业产值、股票价格、空调负荷、电力负荷等非线性与线性交织的复杂时间序列预测时，均表现出良好的预测能力[18-19]。

因此针对旅游突发事件时期客流量明显非线性与线性的特点，本文将SVR和ARIMA混合，实现客流量预测，同时根据突发事件客流量非线性和线性的混沌动态等特征，用CPSO选择SVR的自由参数，将SVR、CPSO和ARIMA结合，充分利用各自的优势实现旅游突发事件时期客流量预测。以来自黄山风景区汶川地震时期相关客流量数据进行应用分析，验证混合预测方法的有效性和准确性。

2 旅游突发事件客流量混合预测方法原理

2.1 SVR原理

对于非线性回归问题，SVR的基本思想是引进核函数k(x,x′)，把问题转化为高维空间(Hilbert空间) 中的线性回归问题，从而构造决策函数[20]。在高维空间里存在线性函数f，可以较好反映出输入变量与输出变量关系，即为所述SVR函数：

f(x)=wTφ(x)+b

φ:Rn→F,w∈F

(1)

引入结构风险函数:

(2)

这里f(·)表示复杂度的项，‖w‖2表示描述函数，C为是折中模型复杂度和经验风险的常数。|yi-f(xi)|是ε不敏感损失函数，它用以偏差控制，让估计更具有鲁棒性。|yi-f(xi)|具体表述为：

(3)

上述函数回归问题等价于下列最小化代价泛函：

(4)

上式中ξi*,ξi为松弛变量，目的是使(4)式的解存在。引入Lagrange函数求该优化问题结合KKT条件，求出所需回归函数：

(5)

ai为Lagrange乘子，ai∈[0,C]，k(xi,x)=φ(xi)φ(x)是满足Mercer条件的核函数，这里选用宽度为σ的Gaussian径向基核函数，得到最终的回归函数：

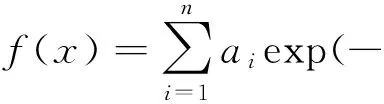
(6)

xi为训练年份输入向量，x为预测年份输入向量，b为阈值。

2.2 CPSO参数寻优

SVR预测性能受到自由参数C、ε和σ的影响，基于突发事件时期旅游客流量特点，本文选取CPSO实现对三个自由参数的寻优。通过将混沌优化算法中的局部搜索(Chaotic Local Search, CLS)和自适应惯性权重因子(Adaptive Inertia Weight Factor, AIWF)引入，利用CLS局部搜索能力和AIWF的全局搜索能力，找出最优参数，克服了PSO局部搜索能力弱、局部最优的限制，实现了全局搜索能力和局部搜索能力的统一[21]。

2.2.1 自适应惯性权重因子(AIWF)

在PSO算法中，每个优化问题的潜在解称之为“粒子”。每个粒子对对应一个由适应度函数决定的适应值(fitness value)。粒子i在n维空间里的位置表示为一个矢量。由于在SVR模型有3个自由参数，因此，在n维状态空间里，第i个粒子在n维空间的位置，第i个粒子的飞行速度，其搜寻到的最优位置分别描述为[22]：

x(k)i=(x(k)i,1,x(k)i,2,…,x(k)i,n)

v(k)i=(v(k)i,1,v(k)i,2,…,v(k)i,n)

p(k)i=(p(k)i,1,p(k)i,2,…,p(k)i,n)

k=C,ε,σ,i=1,2,…,N

(7)

所有粒子x(k)=(x(k)1,x(k)2,…,x(k)N)的全局最优解为：

p(k)g=(p(k)g,1,p(k)g,2,…,p(k)g,n)

k=C,ε,σ,i=1,2,…,N

(8)

然后每个粒子根据如下进化公式来更新自己的速度和新位置：

v(k)i(t+1)=wv(k)i(t)+c1r1(p(k)i-

x(k)i(t))+c2r2(p(k)g-x(k)i(t))

x(k)i(t+1)=x(k)i(t)+v(k)i(t+1)

k=C,ε,σ,i=1,2,…,N

(9)

在粒子群算法中，能否有效的发现最优解的关键在于惯性权重w。w越大，它越会促进粒子趋向于全局搜索；当w越小时，它越会促进粒子趋向于局部搜索。AIWF可以通过以下公式有效地调整上述PSO的权重[23]：

(10)

这里wmin-w最小值、wmax-w最大值，favg-平均适应值、fmin-最小适应值，f-当前适应值。上式可以看出，w随着粒子适应值改变而变化，适应值低的粒子被保留下来，适应值高于favg的粒子被淘汰。AIWF为保持种群多样性、收敛能力提供了一种良好方法，保证了PSO的全局最优性。

2.2.2 混沌局部搜索(CLS)

CLS的优势在于：当粒子陷入早熟时，利用CLS能使粒子跳出局部最优，从而可以快速搜索到PSO中全局最优解fglobal best i，有效的弥补了PSO小范围内搜索能力弱的缺陷。通常情况下，CLS以Logistic方程为基础，具体定义如下：

(11)

(12)

(13)

(14)

具体的CPSO-SVR方法流程如图1所示。

图1 CPSO-SVR流程图

2.3 ARIMA模型原理

ARIMA是在经典时间序列预测中使用最广泛和最灵活的一种预测模型。它的原理为：对于非平稳的时间序列，用若干次差分(差分的次数记为d)使其成为平稳序列，再用 ARMA(p,q)模型对该平稳序列建模，之后经反变换得到原序列[25]。通常情况下ARIMA模型的一般形式为ARIMA(p,d,q)，模型的一般公式表示为：

yt=θ0+φ1yt-1+φ2yt-2+…+φpyt-p

εt-θ1εt-1-θ2εt-2-…-θqεt-q

(14)

步骤1 时间序列平稳性检验。平稳性是使用ARIMA模型预测的必要条件，因此需要对时间序列的平稳性进行检验。根据Box和Jenkins观点，用自相关函数(AutocorrelationFunction,ACF)、偏自相关函数(PartialAutocorrelationFunction,PACF)可以实现对时间序列平稳性的识别。当ACF快速接近于0时，则该时间序列为平稳序列；如果时间序列表现出一定的趋势性和异方差，需对数据进行差分处理和数据转换处理，如对数转换。

步骤2 模型识别。通过对时间序列自相关图和偏自相关图分析，估计p、q的值，以此为基础，利用AIC和SIC准则确定ARIMA模型的最佳阶数。

步骤3 参数估计和模型检验。参数估计的目的是为了找到最合适的参数使得模型预测误差达到最小。方法一般采用极大似然估计(MaximumLikelihoodEstimation，MLE)。同时将估计参数在模型中进行系数显著性、残差序列、拟合度、AIC值和SIC值等检验，如果检验不恰当则重新对参数进行估计。

步骤4模型预测。将获得最合适参数的ARIMA进行预测。

在上述四个步骤中，步骤1-3往往要重复几次才能获得满意的模型。

2.4 基于SVR和ARIMA的混合预测方法原理

上述文献中提到的混合预测模型，均先用ARIMA预测，再用ANN或者SVR预测残差。在本文里，由于突发事件客流量受多种因素影响，输入变量为多变量，而ARIMA作为单变量模型，无法实现多变量的输入。因此本文先利用SVR对突发事件客流量进行预测，然后ARIMA模型对SVR预测的残差进行预测；最后将SVR预测值与ARIMA预测值相加即为最终预测值。具体的步骤如下：

3 实验过程和结果讨论

3.1 数据来源

由于黄山是著名的山岳风景区，因此在各类旅游突发事件中，以自然灾害为主的突发事件对其影响最突出。2008年5月12号，四川汶川发生地震，对当地的旅游资源及旅游接待设施产生巨大的危害，黄山风景区的客流量也受到很大的冲击。因此本文选用黄山风景区汶川地震前后的相关客流量数据，具有一定的典型性。选用数据从2008.2.12-2008.6.30日之间数据集，包括每日客流量、每日八点前客流量，各140条数据。具体如图2所示。

图2 汶川地震前后每日客流量

从图中可以看出，5月本是黄山风景区旅游旺季，但是从5.12以后客流量明显下降，持续走低，5、6月份的分月比重指数[27](即每月客流量除以全年的客流量)分别为7.62%和5.77%，远远低于2009(11.63%、7.19%)、2010(11.18%、9.38%)及2011(11.49%、6.85%)年同等月份，说明地震这种突发的自然灾难性事件对客流量造成极大的影响，原有模式被打破，非线性与线性交织的随机性明显。

3.2 混合预测方法实验过程

将2008.2.12-2008.5.12期间共计91个数据作为训练集，2008.5.13-2008.6.30期间共计49个数据作为测试集，它们为SVR输入，客流量预测值为SVR输出，在Matlab(R2010b)试验平台上按照CPSO-SVR流程反复测试。CPSO各参数设置如表1所示，其中C的范围为[0,100]，ε的范围为[0,1]，σ的范围为[0,10]。由于在CPSO算法中，每个优化问题的潜在解称之为“粒子”，每个粒子对应着SVR自由参数对(C,ε,σ)，对应参数的粒子分别称之为C粒子、ε粒子 和σ粒子，它们最大速度vmax被分别限制在每个参数范围15%的搜索空间内。经过CPSO参数寻优，最终获得SVR模型的最优参数值分别为：C=17.9597，σ=2.5567，ε=0.0191，CVmse=0.0050，支持向量个数为23，b=-0.5857。模型预测的最后结果及残差如图3所示。

表1 CPSO参数设置

图3 汶川地震后每日客流量预测情况(5.13-6.30)

从图可以看出，49个预测值中，残差以负值为主：负值43个，正值仅6个。说明在预测过程中预测值普遍高于实际值，可能原因在于：由于受汶川地震突发事件影响，客流量突然受到影响，而CPSO-SVR方法无法很快适应这种突如其来数据量的变化，仍然按照其原有的轨迹进行预测，因此出现预测值大部分高于实际值现象。此时预测误差为22.92%。显然，这种预测误差较大，指导意义不大。再通过Eviews6.0软件，对残差的平稳性进行检验，发现一阶差分后数据呈现平稳性，故d=1，对一阶差分后残差序列的自相关和偏相关分析(如图4所示)，进一步确定了该模型结构为ARIMA(1,1,1)。

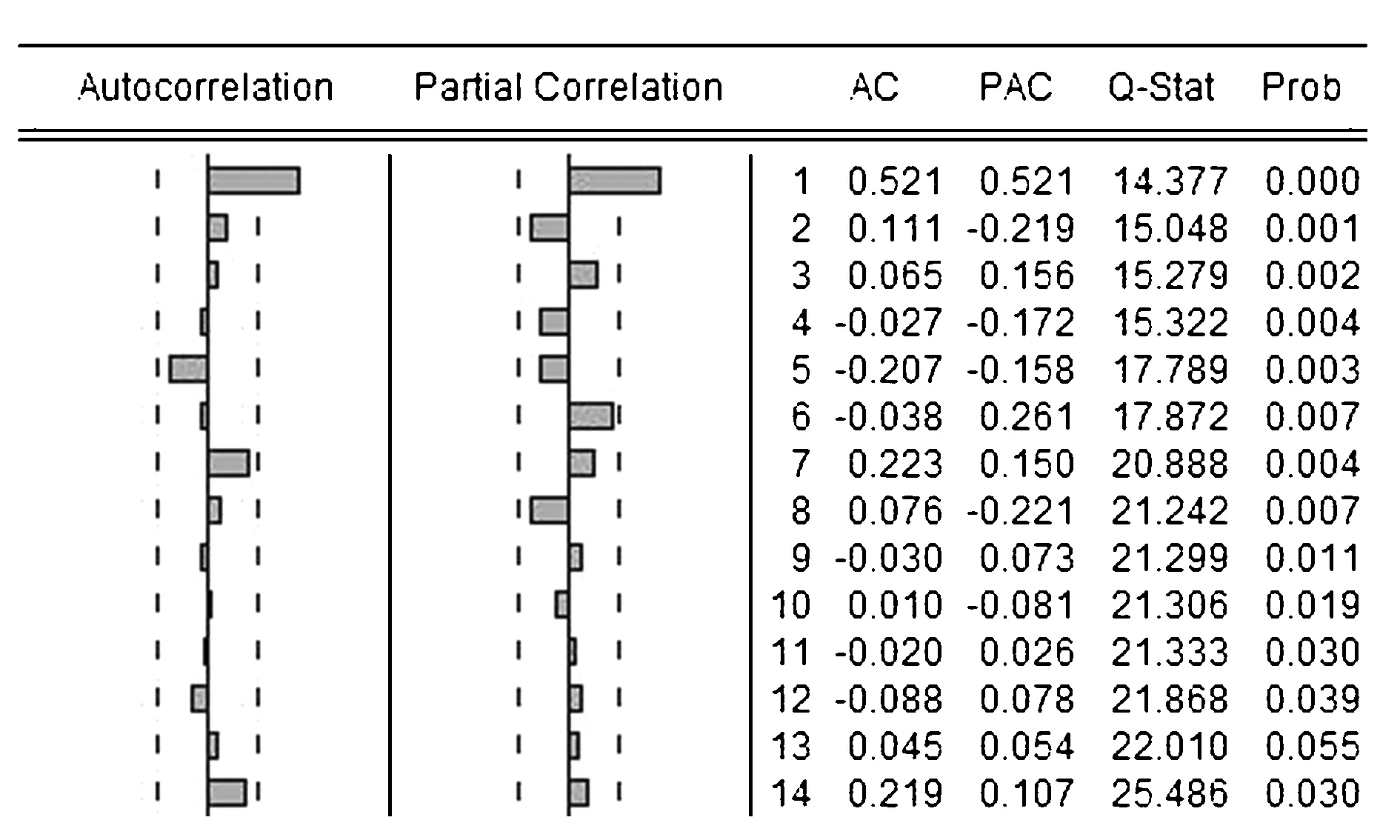
图4 残差ACF和PACF分析

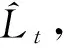
图5 汶川地震后客流量预测值不同方法比较

图6 不同预测方法误差比较

3.3 实验结果讨论

通过图5、图6和表2可以看出，在49天的预测值里，用SVR和ARIMA混合预测结果与实际值最接近的有33天，CPSO-SVR为13天，PSO-SVR仅3天，误差情况SVR和ARIMA混合法最小，其次CPSO-SVR，最后为PSO-SVR。为进一步比较预测值和实际值偏离程度，本文选用平均绝对误差(Mean Absolute Error, MAE)、平均绝对百分误差(Mean Absolute Percentage Error, MAPE)、均方误差(Root Mean Square Error, RMSE)及相关系数R等作为评价指标[28-29]。具体评价指标如表3所示。

注：*号表明该预测值最接近实际值。

表3 不同预测方法评价指标值

从上表可以看出， SVR和ARIMA混合预测方法MAE、MAPE及RSME均低于CPSO-SVR和PSO-SVR；相关系数R高于CPSO-SVR和PSO-SVR，进一步说明混合预测方法效果优于CPSO-SVR和PSO-SVR。可能的原因在于：

(1)汶川地震发生后客流量偏离以往模式，非线性和线性相结合的随机性特点占主导地位，在SVR和ARIMA的混合预测方法中，SVR具有处理非线性的能力，ARIMA对线性趋势有很好的预测能力，两者结合抓住突发事件发生时客流量特点，因此混合预测方法能力较单个的SVR预测方法得到提高。

(2)CPSO能够根据客流量特点更好实现对SVR自由参数快速寻优，加入CPSO的混合预测方法，预测准确性更好。

(3)在预测的过程中也发现，在CPSO-SVR和PSO-SVR的比较中，前者预测能力高于后者，这充分说明了加入混沌局部搜索CLS和自适应惯性权重因子AIWF的CPSO算法寻优能力高于单纯的PSO算法。

(4)三种方法在预测过程中，预测值普遍高于实际值(如图6误差表所示)，可能的原因在于SVR此时的预测值为没有发生地震时正常状态下预测值，按照以往惯例，黄山此时是旅游旺季，但突然发生的地震破坏了客流量以往模式，因此造成预测值普遍高于实际值的现象。这同时也说明SVR在面临一些转折点、突发事件时，不能很快适应客流量突然的变化，预测能力受到一定挑战，但是可以通过和其他合适方法的混合来弥补SVR在预测方面存在的局限性，本节的混合预测方法正是说明了这个道理。

3.4 混合预测方法的局限性

由于国内景区实行信息化的时间较短，旅游突发事件发生后短期客流量数据获取有限，本文仅用汶川地震发生前后不到5个月的客流量数据对混合方法进行训练、测试，给出的数据个数较少，规律表现的不是很明显，如有大量历史同等数据如2008年及以前该期间的数据输入时，模型的有效性将会得到更好的体现；另外其他的一些较大的对旅游景区产生直接影响的突发事件如SRAS由于无记录的客流量数据，因此无法用该模型进行验证。从某种意义上说该混合方法存在一定的局限性。但是随着智慧景区的实施推广，数据的收集将变得越来越容易，因此该方法将会得到更广泛的推广应用。

4 结语

旅游突发事件经常会给旅游景区造成巨大的影响，其中最直接的就是客流量的剧烈波动。这种剧烈的波动，偏离原有的客流量运行模式，呈现出复杂非线性和线性相结合的随机性特点。旅游突发事件时期客流量的准确预测能够使景区管理者合理配置资源，及时快速地进行相应的应急管理。本文提出了一种SVR和ARIMA的混合预测方法。基于CLS和AIWF的PSO算法找出SVR最优自由参数，研究结果表明：本文提出的混合预测方法效果显著优于其他方法。该混合方法中涉及到的SVR和ARIMA预测方法，均在各自的应用领域里应用广泛，因此混合使用时，操作方法简单，可行性较高。该方法不仅在旅游突发事件时期对客流量具有良好的预测效果，在类似的行业领域内面临同样状况时也能进行预测，具有一定的推广性和应用价值。

[1] Wang Y S. The impact of crisis events and macroeconomic activity on Taiwan's international inbound tourism demand [J]. Tourism Management, 2009, 30(1): 75-82．

[2] Faulkner B, Russell R. Chaos and complexity in tourism: In search of a new perspective [J]. Pacific Tourism Review, 1997, 1(2): 93-102.

[3] Prideaux B, Laws E, Faulkner B. Events in Indonesia: Exploring the limits to formal tourism trends forecasting methods in complex crisis situations [J]. Tourism Management, 2003, 24(4): 475-487.

[4] Goh C, Law R. Modeling and forecasting tourism demand for arrivals with stochastic nonstationary seasonality and intervention [J]. Tourism Management, 2002, 23(5): 499-510.

[5] Law R. The impact of the Asian financial crisis on Japanese demand for travel toHong Kong: A study of various forecasting techniques[J]. Journal of Travel & Tourism Marketing, 2001, 10(2-3): 47-65.

[6] Huang J H, Min J C H. Earthquake devastation and recovery in tourism: The Taiwan case [J]. Tourism Management, 2002, 23 (2): 145-154.

[7] Min J C H. The effect of the SARS illness on tourism in Taiwan: An empirical study [J]. International Journal of Management, 2005, 22(3): 497-508.

[8] Kuo H I, Chen C C, Tseng W C, et al. Assessing impacts of SARS and Avian Flu on international tourism demand to Asia [J]. Tourism Management, 2008, 29(5): 917-928.

[9] Wang Y S. The impact of crisis events and macroeconomic activity on Taiwan's international inbound tourism demand [J]. Tourism Management, 2009, 30(1): 75-82.

[10] Fang Yue. Forecasting combination and encompassing tests [J]. International Journal of Forecasting, 2003, 19(1):87-94.

[11] Wong K K F, Song H Y, Witt S F, et al. Tourism forecasting: To combine or not to combine [J]. Tourism Management,2007,28(4):1068-1078.

[12] Shahrabi J, Hadavandi E, Asadi S. Developing a hybrid intelligent model for forecasting problems: Case study of tourism demand time series [J]. Knowledge-Based Systems, 2013, 43(2): 112-122.

[13] 张金良.电力市场环境下的短期电价混合预测模型研究[D].北京：华北电力大学，2011．

[14] Khashei M, Bijari M. A novel hybridization of artificial neural networks and ARIMA models for time series forecasting [J]. Applied Soft Computing, 2011, 11(2): 2664-2675.

[15] Fard A K, Akbari-Zadeh M R. A hybrid method based on wavelet, ANN and ARIMA model for short-term load forecasting [J]. Journal of Experimental & Theoretical Artificial Intelligence, 2014, 26(2): 167-182.

[16] Li Xuemei, Ding Lixing, Deng Yuyan, et al. Hybrid support vector machine and ARIMA model in building cooling prediction[C].Proceedings of 2010 International Symposium on Computer Communication Control and Automation (3CA), Tainan,Taiwan,May 5-7, 2010.

[17] 王书平, 胡爱梅, 吴振信. 基于多尺度组合模型的铜价预测研究[J]. 中国管理科学, 2014,22(8):21-28.

[18] Chen K Y, Wang C H. A hybrid SARIMA and support vector machines in forecasting the production values of the machinery industry in Taiwan [J]. Expert Systems with Applications, 2007, 32 (1): 254-264.

[19] Pai P F, Lin C S. A hybrid ARIMA and support vector machines model in stock price forecasting [J]. Omega, 2005, 33(6): 497-505.

[20] 姚智胜, 邵春福, 熊志华. 基于小波包和最小二乘支持向量机的短时交通流组合预测方法研究[J]. 中国管理科学, 2007, 15(1): 64-68.

[21] 李炳宇,萧蕴诗,汪 镭.一种求解高维复杂函数优化问题的混合粒子群优化算法[J].信息与控制, 2004, 33(1): 27-30．

[22] Hong W C. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model [J]. Energy Conversion and Management, 2009, 50(1): 105-117.

[23] Liu Bo, Wang Ling, Jin Yihui, et al. Improved particle swarm optimization combined with chaos [J]. Chaos, Solitons & Fractals, 2005, 25(5): 1261-1271.

[24] 刘军民,高岳林.混沌粒子群优化算法[J].计算机应用, 2008, 28(2): 322-325.

[25] 韩超,宋苏,王成红.基于ARIMA 模型的短时交通流实时自适应预测[J].系统仿真学报, 2004, 16(7): 1530-1532.

[26] 谭满春,冯荦斌,徐建闽.基于ARIMA 与人工神经网络组合模型的交通流预测[J].中国公路学报, 2007, 20(4): 118-121.

[27] 曹伟宏,何元,李宗省,等.丽江旅游气候舒适度与年内客流量变化相关性分析[J].地理科学, 2012, 32(12): 1459-1564.

[28] 赛英,张凤廷,张涛.基于支持向量机的中国股指期货回归预测研究[J].中国管理科学, 2013, 21(3): 35-39.

[29] 徐达宇,杨善林,罗贺,基于广义模糊软集理论的云计算资源需求组合预测研究[J].中国管理科学,2015,23(5): 56-64.

The Research of Tourist Flow Hybrid Forecasting Model for Tourism Emergency Events

CHEN Rong1, LIANG Chang-yong2, LU Wen-xing2, DONG Jun-feng2，GE Li-xin3

(1.Department of Economic and Management, BengBu University, Bengbu 233000，China; 2.School of Management, HeFei University of Technology, Hefei 230009,China; 3.Department of Science, BengBu University, Bengbu 233000，China)

Because of sudden explosiveness and destructiveness as well as information asymmetry caused by tourism emergency events, the tourist flow deviates from original patterns and presents nonlinear and linear features, which causes a great difficulty to tourist flow forecasting. Traditional forecasting methods cannot solve this complicated problem. The article proposes a kind of tourist flow hybrid forecasting model for tourism emergency events which include two methods. One method is Support Vector Regression (SVR). It has good ability to deal with nonlinear and small sample problems and has been successfully used in many forecasting fields by researchers. The other method is Autoregressive Integrated Moving Average (ARIMA) which can deal with linear problem easily. At same time, the three parametersC,ε,σofSVRaffecttheaccuracyofforecast.AkindofChaosParticleSwarmOptimization(CPSO)isusedinthearticle.BythelocalsearchabilityofChaoticLocalSearch(CLS)aswellasglobalsearchabilityofAdaptiveInertiaWeightFactor(AIWF)inCPSO,theoptimalparametersC,ε,σofSVRcanbefoundeffectively.Thedetailprocessoftouristflowhybridforecastingmodelisasfollow.FirstlySVRisusedtoforecasttouristflowduringemergencies.Meanwhile,CPSOisimplementedtoselecttheSVRparameters;SecondlyARIMAmodelisprovidedtoforecastresidualsequenceofforecastingvalues.Finallytwopredictedvalueswillbeadded,whichleadstothefinalpredictedvalues.DatasetfromMountHuangshanduringWenchuanEarthquakesperiodareusedtovalidatetheeffectivenessofthehybridmodels.ThenumberofthedataisfromFebruary12, 2008toJune12, 2008,includingthedailytouristflowanddailytouristflowbeforeeighto'clock.TheresultsshowthatthehybridapproachesaresignificantlyhigherinaccuracythanCPSO-SVRandPSO-SVR.,whichprovideaneffectivechoicetotourismemergencyeventsflowforecastingaswellassimilarindustriesfacingthesamesituation.Nextresearcheswillfocusontouristflowforecastingunderthebackgroundofbigdata.

SVR;ARIMA;CPSO;tourism emergeney everts;tourist floco forecasting

1003-207(2017)05-0167-08

10.16381/j.cnki.issn1003-207x.2017.05.020

2016-01-07；

2016-04-27

国家自然科学基金资助项目(71331002, 71271072, 71301037, 71301040)；安徽高校自然科学研究重点项目(KJ2015A143)；安徽省教育厅2016年高校优秀拔尖人才培育资助重点项目(gxfxZD2016283);蚌埠学院国家级项目培育基金项目

梁昌勇(1965-)，男(汉族)，安徽肥西人，合肥工业大学管理学院教授，博士生导师，研究方向：管理信息系统、行为决策、信息管理与公共政策、云计算技术等，E-mail: cyliang@hfut.edu.cn.

TP181

A