一种强兼容性的灰色通用预测模型及其性质研究

曾 波，刘思峰，曲学鑫

(1.重庆工商大学商务策划学院，重庆 400067; 2.南京航空航天大学经济与管理学院，江苏 南京 210016; 3.重庆工商大学国家智能制造服务国际科技合作基地，重庆 400067)



一种强兼容性的灰色通用预测模型及其性质研究

曾 波1，刘思峰2，曲学鑫3

(1.重庆工商大学商务策划学院，重庆 400067; 2.南京航空航天大学经济与管理学院，江苏 南京 210016; 3.重庆工商大学国家智能制造服务国际科技合作基地，重庆 400067)

预测建模对象的复杂性导致了灰色模型形式的多样性与结构的互不兼容性，通过在灰色模型中引入因变量滞后项、线性修正项及常数修正项，构建了一种强兼容性的灰色通用预测模型(CGPM)，证明了CGPM模型与多变量GM(1, N)模型与GM(0, N)模型及单变量GM(1, 1)模型、DGM(1, 1)模型及NDGM(1, 1)模型的转换条件与等价性质，最后通过实例对CGPM模型的有效性进行了验证；研究成果对优化灰色模型结构、提高灰色模型通用性与普适性具有积极意义。

灰色理论；预测模型；强兼容性；模型转换

1 引言

长期以来，定量预测研究方法一直为以大样本数据为基础的数理统计方法所主导，为了解决“小数据、不确定性”系统的分析、预测、决策与控制问题，上世纪80年代初，华中工学院邓聚龙教授提出了面向“小样本、贫信息”系统的灰色理论[1]，该理论依据信息覆盖，通过序列生成和灰色模型探索事物运动的现实规律，其特点是“少数据建模”。其中，灰色预测模型是灰色理论的重要组成部分，经过三十多年的发展，它已在农业、工业、社会、经济、交通、能源、医疗等众多领域得到了广泛地应用，成功地解决了生产、科研、管理中的大量重要问题，在该过程中，灰色模型也由原始的GM(1,1)模型扩展出GM(1,N)、GM(0,N)、GM(2,1)、DGM(1,1)、NDGM(1,1)、GM(1,1)幂模型等多种新的预测模型类别；预测对象也拓展到数列预测、区间预测、灰色灾变预测、波形预测、系统预测[2-3]等。

为了提高灰色预测模型的模拟与预测性能，研究人员从初始值[4-5]、背景值[6-7]、光滑度[8-9]、建模对象[10-13]、建模机理[14-18]、模型性质[19-21]、模型组合[22]等角度对灰色预测模型进行了大量深入系统研究，推动了灰色预测模型理论体系的发展和完善。然而，由于不同灰色预测模型通常具有不同的模型结构、建模条件与适用范围，导致现有灰色模型之间的兼容性较差，然而现实世界的复杂性导致很多情况下建模对象并不完全满足某一类模型的建模条件，而是同时兼具多个模型的对象特征，需要通过模型整合才能实现对复杂系统的客观模拟，在这样的情况下如何实现模型结构的集成与兼容是值得深入研究的一个重要内容。

本文通过在灰色模型中引入因变量滞后值、线性修正项及常数修正项，构建了一种强兼容性的灰色通用预测模型(CGPM)，该模型可以通过参数变化实现与GM(1,N)模型、GM(0,N)模型、GM(1,1)模型、DGM(1,1)模型及NDGM(1,1)模型的等价转换，从理论上证明了CGPM模型能实现对单变量序列与多变量序列的完全兼容；同时由于CGPM模型还可以转化为DGM(1,1)模型及NDGM(1,1)模型，因此CGPM模型同样可以实现对齐次及非齐次指数序列的无偏模拟。CGPM模型结构基于不同建模对象的动态调整能力，解决了传统主流灰色预测模型之间的兼容性问题，对提高灰色模型通用性与普适性具有积极意义。换言之，在运用CGPM模型解决实际管理预测问题的过程中，不需要首先分析建模数据序列的齐次或非齐次指数特征，也不必考虑因变量序列(系统特征序列)受到何种因素的影响，CGPM模型凭借其强大的兼容能力，能够根据建模序列的数据特征进而实现其模型结构的动态优化，从而实现对预测对象的有效模拟及科学预测。

2 预备知识

定义1[2]. 设X(0)为1-等时距非负原始数据序列：

X(0)=(x(0)(1),x(0)(2),…,x(0)(m))

其中x(0)(k)≥0，D为序列算子，

X(0)D=(x(0)(1)d,x(0)(2)d,…,x(0)(m)d)

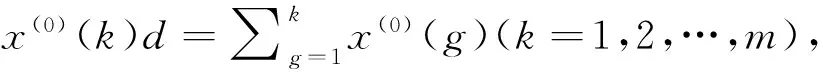
X(0)D=X(1)=(x(1)(1),x(1)(2),…,x(1)(m))

X(0)Dr=X(r)=(x(r)(1),x(r)(2),…,x(r)(m))

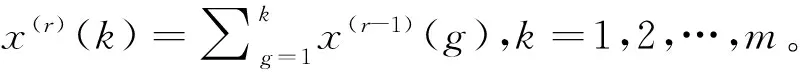
可见定义1中的变量r代表序列的累加次数，当r=0表示该序列为原始序列，当r=1则表示该序列为1次累加生成序列，以此类推。

定义2[2]. 设序列X(0)、X(1)如定义1所示，则称序列Z(1)为X(1)的紧邻均值生成序列：

Z(1)=(z(1)(2),z(1)(3),…,z(1)(m))

其中z(1)(k)=0.5×(x(1)(k)+x(1)(k-1))，k=2,3,…,m。

定义3[2]. 设序列X(0)、X(1)及Z(1)分别如定义1及定义2所示，则称：

x(0)(k)+az(1)(k)=b

为含一个变量的一阶方程灰色系统预测模型，简称GM(1,1)模型。

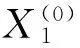
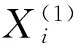
则称：

(1)

为含N个变量的零阶方程灰色系统预测模型，简称GM(0,N)模型。称：

(2)

为含N个变量的一阶方程灰色系统预测模型，简称GM(1,N)模型。

注：在以往关于多变量灰色系统预测模型的定义中，通常用N表示变量个数，而用n表示序列中元素个数。本文为避免混淆，用字母m代替n表示序列中元素个数，从而确保对GM(0,N)及GM(1,N)模型的定义更清晰准确。

定义5[12]. 设序列X(0)及X(1)如定义1所示，则称：

x(1)(k+1)=β1x(1)(k)+β2

为GM(1,1)模型的离散形式，或离散GM(1,1)模型，简称DGM(1,1)模型。

定义6[2]. 设序列X(0)及X(1)如定义1所示，则称：

x(1)(k+1)=β1x(1)(k)+β2k+β3

为近似非齐次指数离散灰色模型，简称NDGM(1,1)模型。

3 模型构建与模型性质

(3)

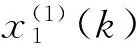
P=(BTB)-1BTY

(4)

其中B,Y分别为：B=

根据定义1，可知CGPM模型的还原式为

(5)

性质1：GM(1,N)模型及CGPM模型分别如定义4及定义7所述，则当h1≠0，h2=0，h3=0且N>1时，CGPM模型即为GM(1,N)模型。

证明：根据公式(3)可知， 当h2=0且h3=0时

(6)

公式(6)可变形为：

(7)

令h1=(1-0.5a)/(1+0.5a)，则公式(7)可进一步变形为：

(8)

整理公式(8)可得，

(9)

根据定义1可知，

(10)

(11)

将公式(10)及公式(11)代入公式(9)，可得：

(12)

公式(12)中，a及bt(t=2,3,…N)均为常数，令ct=bt/(1+0.5a)，则公式(12)可简化为：

(13)

公式(13)即为含N个变量的一阶方程灰色预测模型，即GM(1,N)模型。 证明结束。

性质2：GM(0,N)模型及CGPM模型分别如定义4及定义7所述，则当N>1，h1=0且h2=0时，CGPM模型即为GM(0,N)模型。

证明: 当N>1，h1=0且h2=0时，根据公式(3)可知：

(14)

公式(14)即为含N个变量的零阶方程灰色预测模型，即GM(0,N)模型。 证明结束。

性质3：GM(1,1)模型及CGPM模型分别如定义3及定义7所述，则当h2=0，h1·h3≠0且N=1时，CGPM模型即为传统的GM(1,1)模型。

证明: 根据公式(3)可知，当h2=0，h1≠0，h3≠0且N=1时：

(15)

令h1=(1-0.5a)/(1+0.5a)，则公式(15)可进一步变形为：

(16)

整理公式(16)，可得：

(17)

根据定义1及定义2，公式(17)可变形为：

(18)

其中b=(1+0.5a)h3，公式(18)即为单变量1阶方程灰色模型，即GM(1,1)模型。

证明结束。

性质4：DGM(1,1)模型及CGPM模型分别如定义5及定义7所述，则当h1·h3≠0，h2=0且N=1时，CGPM模型即为DGM(1,1)模型。

证明：当h1·h3≠0，h2=0且N=1时，根据定义7可知，

(19)

在上式中，h1及h3均为常数，令β1=h1，β2=h3则公式(19)变形为：

x(1)(k)=β1x(1)(k-1)+β2

(20)

公式(20)即为DGM(1,1)模型。证明结束。

性质5：NDGM(1,1)模型及CGPM模型分别如定义6及定义7所述，则当h1·h2·h3≠0且N=1时，CGPM模型即为NDGM(1,1)模型。

证明：当h1·h2·h3≠0且N=1时，根据定义7可知，

(21)

公式(21)可变形为：

(22)

在上式中，h1、h2及h3均为常数，令β1=h1，β2=h2，β3=h3-h2，则公式(22)变形为：

x(1)(k+1)=β1x(1)(k)+β2k+β3

(23)

公式(23)即为NDGM(1,1)模型。 证明结束。

根据性质5，可以进一步得到如下推论。

推论1：CGPM模型定义7所述，则当h1·h2·h3≠0且N=1时，CGPM模型能实现对齐次指数序列及非齐次指数序列的无偏模拟。

推论2：CGPM模型定义7所述，则当h1·h2·h3≠0且N=1时，CGPM模型能实现对线性函数序列的无偏模拟。

推论1及推论2可通过矩阵运算或克莱姆法则来加以证明，此处略。

根据CGPM模型的上述性质，可得CGPM模型与其他模型之间拓展关系，如图1所示。

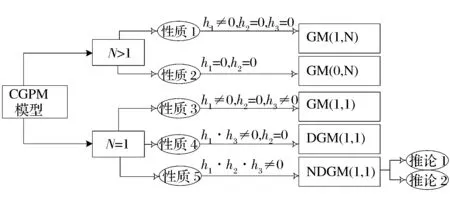
图1 CGPM模型与其他模型的拓展关系示意图

从图1中可以看出，CGPM模型可以通过模型参数的变化实现与多变量GM(1,N)模型、GM(0,N)模型及单变量GM(1, 1)模型、DGM(1, 1)模型及NDGM(1, 1)模型的转换，表明CGPM模型更具兼容性、通用性与泛化能力。

4 模型比较分析

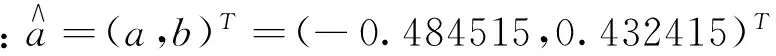
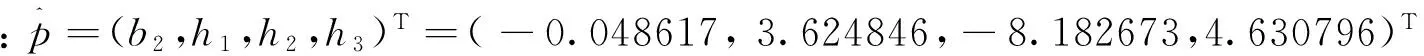
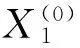
从表2可以看出，CGPM模型可以实现对单变量序列的模拟，且其模拟性能优于经典的GM(1,1)模型，再次说明CGPM具有较强的模拟能力。

表1 GM(0,2)模型与CGPM模型对多变量序列的模拟值与模拟误差

表2 GM(1,1)模型与CGPM模型对单变量序列的模拟值与模拟误差

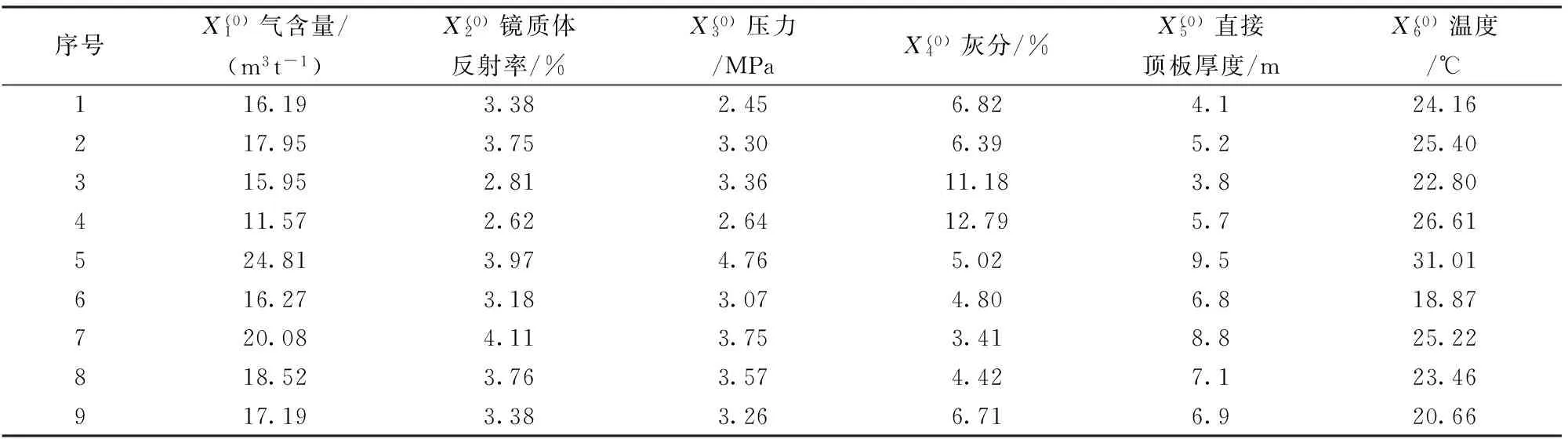
表3 沁水煤田晋城矿区3号煤层参数统计表

(a)CGPM模型

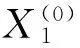
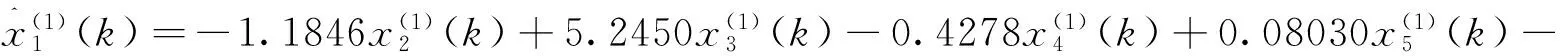
(24)

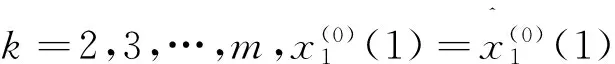
(b)GM(0,6)模型

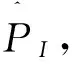
系统特征序列的GM(0,6)模型为：

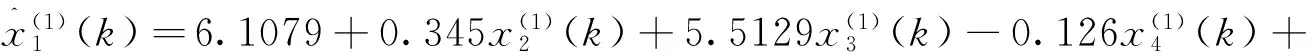
(25)

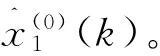
CGPM模型及GM(0,6)模型的模拟结果如表4所示。

5 结语

由于不同灰色预测模型通常具有不同的模型结构、建模条件与适用范围，导致了灰色模型之间的兼容性差，本文通过在灰色模型中引入因变量滞后值、线性修正项及常数修正项，构建了一种强兼容性的灰色通用预测模型(CGPM)，该模型可以通过参数变化实现与现有主流灰色预测模型的等价转换，能实现对单变量序列与多变量序列及齐次与非齐次指数序列的有效模拟。研究成果解决了传统主流灰色预测模型之间兼容性差的问题，对提高灰色模型通用性与普适性，促进灰色预测模型与实际管理问题的有效对接，具有积极意义。如何实现对CGPM模型的初始值、背景值、分数阶及病态性等问题的的系统研究，是本研究团队下一步的主要工作内容。

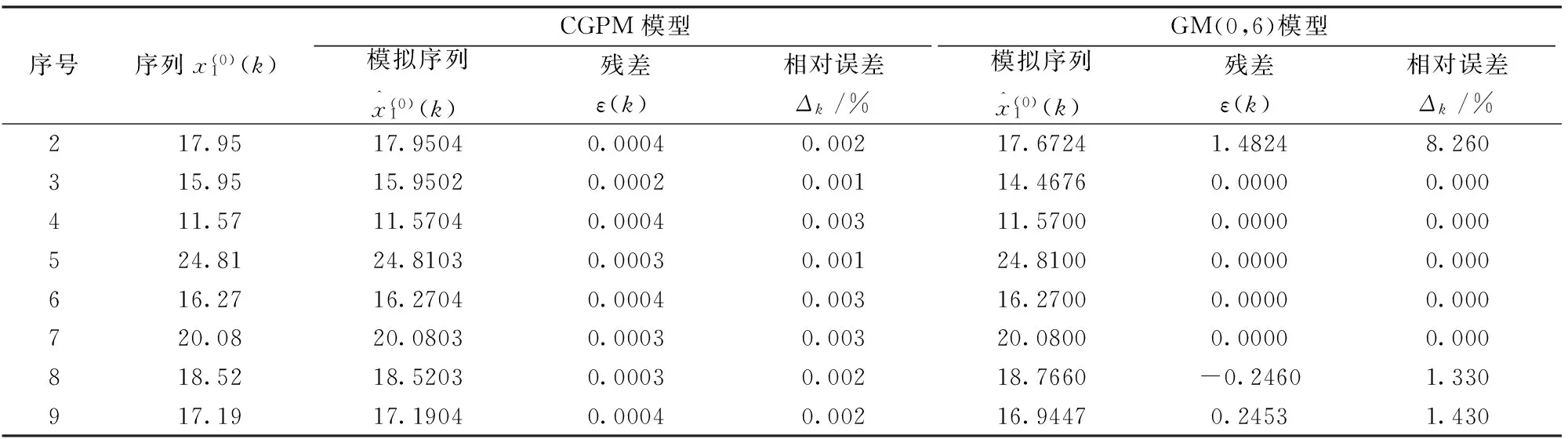
表4 CGPM模型与GM(0,6)模型的模拟值与模拟误差

[1] Deng Julong. Control problem of grey systems [J]. System Control Letter, 1982, 1(5): 288-294.

[2] Liu Sifeng, Lin Y. Grey system theory and applications [M]. Berlin Heidelberg: Springer-Verlag, 2010.

[3] Xia Min, Wong W K. A seasonal discrete grey forecasting model for fashion retailing [J].Knowledge-based Systems, 2014, 57: 119-126.

[4] 姚天祥, 刘思峰, 党耀国. 初始值优化的离散灰色预测模型[J]. 系统工程与电子技术, 2009, 31(10): 2394-2398.

[5] 戴文战. 基于函数cot(xα)变换及背景值优化的灰色建模[J]. 浙江大学学报(工学版), 2010, 44(7): 1368-1372.

[6]WeiYong,ZhangYi.Acriterionofcomparingthefunctiontransformationstoraisethesmoothdegreeofgreymodelingdata[J].TheJournalofGreySystem.2007, 19 (1):91-98.

[7] 熊萍萍, 党耀国, 姚天祥,等. 灰色Verhulst模型背景值优化的建模方法研究[J]. 中国管理科学, 2012, 20(6):155-159.

[8]WeiYong,ZhangYi.Anessentialcharacteristicofthediscretefunctiontransformationtoincreasethesmoothdegreeofdata[J].TheJournalofGreySystem, 2007, 19(3): 293-300.

[9]ZengBo,ChenGuo,LiuSifeng.Anovelintervalgreypredictionmodelconsideringuncertaininformation[J].JournaloftheFranklinInstitute, 2013,350(10): 3400-3416.

[10]XieNainming,LiuSifeng.Intervalgreynumbersequencepredictionbyusingnon-homogenousexponentialdiscretegreyforecastingmodel[J].JournalofSystemsEngineeringandElectronics, 2015, 26(1): 96-102.

[11] 曾波,刘思峰,孟伟. 具有主观取值倾向的离散灰数预测模型及其应用[J]. 控制与决策, 2012, 27(9): 1359-1364.

[12]XieNaiming,LiuSifeng.Discretegreyforecastingmodelanditsoptimization[J].AppliedMathematicalModeling, 2009,33(2):1173-1186.

[13] 曾波, 孟伟, 刘思峰,等. 面向灾害应急物资需求的灰色异构数据预测建模方法[J]. 中国管理科学, 2015, 23(8): 85-91.

[14] 孟庆良, 何林, 朱慧明,等. 基于GM(1,1)模型的Kano质量要素分类动态预测方法[J]. 中国管理科学, 2015, 23(9):140-145.

[15]LiuJun,XiaoXinping.TherelationshipofdiscretegreyforecastingmodelDGMandGM(1,1)model[J].JournalofGreySystem, 2014, 26(4): 14-31.

[16]XieNaiming,ZhuChaoyu,ZhengJing.Expansionmodelingofdiscretegreymodelbasedonmulti-factorinformationaggregation[J].JournalofSystemsEngineeringandElectronics, 2014, 25(5): 833-839.

[17]XiaoXinping,GuoHuan,MaoShuhua.Themodelingmechanism,extensionandoptimizationofgreyGM(1,1)model[J].AppliedMathematicalModeling, 2014, 38(5-6): 1896-1910.

[18]ChenCI,HuangSJ.ThenecessaryandsufficientconditionforGM(1,1)greypredictionmodel[J].AppliedMathematicsandComputation, 2013, 219(11): 6152-6162.

[19]ZengBo,LiChuan,ChenGuo,etal.Equivalencyandunbiasednessofgreypredictionmodels[J].JournalofSystemsEngineeringandElectronics, 2015, 26(1): 110-118.

[20] 肖新平, 毛树华. 灰预测与决策方法[M]. 北京：科学出版社, 2013.

[21] 郭晓君, 刘思峰, 杨英杰. 基于自忆性原理的多变量MGM(1,m)耦合系统模型构建及应用[J]. 中国管理科学, 2015, 23(11):113-118.

[22] 于志军, 杨善林,章政,等. 基于误差矫正的灰色神经网络股票收益率预测[J].中国管理科学,2015, 23(12):21-26.

ResearchingonAGreyCommonPredictionModelingwithStrongCompatibilityandItsProperties

ZENGBo1,LIUSi-feng2,QUXue-xin3

(1.College of business planning, Chongqing Technology and Business University, Chongqing 400067, China;2.College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;3.National Research Base of Intelligent Manufacturing Service,Chongqing Technology and Business University, Chongqing 400067, China)

The complicacy of predictive modeling object gives rise to the diversity of form and mutual non-compatibility of structure of grey models. A grey common prediction modeling with powerful compatibility (CGPM) is established through putting the lagged item of dependent variable, corrective terms of linear and constant into grey model. The transformation conditions and equivalence properties between CGPM model and multivariable grey models which include GM(1, N) and GM(0, N) and single variable grey models including GM(1, 1), DGM(1, 1) and NDGM(1, 1) are proved in this paper. The effectiveness of CGPM model is verified by some calculation examples. The study findings have some positive significance for optimizing the structure of grey model and improving the commonality and universality of grey model.

grey theory; prediction model; powerful compatibility; model transformation

1003-207(2017)05-0150-07

10.16381/j.cnki.issn1003-207x.2017.05.018

2016-01-25；

2016-05-24

国家自然科学基金资助项目(71271226)；重庆市社科规划委托项目(2016WT37)；重庆市教育科学规划课题(2012-GX-142)；中国科协重大招标项目(2016ZCYJ06)

曾波(1975-)，男(汉族)，四川威远人，重庆工商大学商务策划学院教授，工学博士，研究方向：预测建模方法的研究，E-mail:zbljh2@163.com.

N941.5

A