博弈参与水平对无标度网络上合作行为演化的影响
2017-06-01谢逢洁武小平崔文田陈子凤
谢逢洁,武小平,崔文田,陈子凤
(1.西安邮电大学经济与管理学院,陕西 西安 710061;2.西安交通大学管理学院,陕西 西安 710049)
博弈参与水平对无标度网络上合作行为演化的影响
谢逢洁1,武小平1,崔文田2,陈子凤1
(1.西安邮电大学经济与管理学院,陕西 西安 710061;2.西安交通大学管理学院,陕西 西安 710049)
通过仿真实验分析囚徒困境博弈和雪崩博弈在无标度网络上的动态演化,进而考察个体的博弈参与水平对无标度网络上合作行为演化的影响。在理论模型中,个体的博弈参与水平通过个体每次博弈的交互作用邻居数量来衡量。实验结果表明,个体的博弈参与水平表现出对无标度网络合作行为的正向影响作用,无标度网络上的群体合作水平随着个体博弈的交互作用邻居数量增多而提高。通过结果分析发现,不同连接度的个体在博弈参与水平提高的条件下,均表现出更强的抵御背叛的能力;其主要原因在于,高连接度个体在积极参与博弈的条件下更趋向于合作,进而影响到低连接度个体对合作行为的选择。
无标度网络;囚徒困境博弈;雪崩博弈;合作行为;博弈参与水平
1 引言
理解自利个体如何形成广泛合作是演化博弈理论研究的核心问题。到目前,最为突出的5个解释合作行为的机制包括亲缘选择、团队选择,直接互惠,间接互惠,以及空间结构[1]。
空间结构对群体合作行为的影响研究始于Nowak和May[2]用仿真方法研究空间规则格子上囚徒困境博弈的演化。其研究结果表明,群体可以形成较为广泛的合作,博弈个体在空间规则格子上形成的合作者聚集结构对于广泛合作的产生和维持至关重要。此后,大量研究进一步证明了空间格子对合作行为的促进作用[3-7]。然而,Hauert 和Doebeli[8]的研究工作修正了这个认识。通过在空间格子上研究雪崩博弈的演化,他们发现空间格子对合作行为的抑制作用。空间格子在不同博弈情境下对合作行为的不同作用进一步激发了研究者们对合作行为产生机理的探索。随着复杂网络理论研究的兴起,无标度网络对合作行为的影响作为热点问题受到广泛关注[9-18]。
在复杂网络理论中,一个节点连接的边数定义为该节点的“度(Degree)” ,也称为“连接度”。无标度网络中有少数节点有着非常高的连接度,常被称为高连接度节点或hub 节点,这与度同质的规则格子完全不同。当考虑hub节点所具有的资源优势并以累积收益法度量个体的博弈收益时,无标度网络在囚徒困境博弈和雪崩博弈情境下都对合作行为有着非凡的促进作用[9-10],其上的合作水平远远高于规则格子上的合作水平。但是,文献[11]提出,hub节点的连接数量非常高,在有限的时间和精力条件下,可能使得他与每个邻居的交互作用频率低于那些低连接度节点,进而建议用平均收益度量个体的博弈收益。研究发现,当用平均收益度量个体的博弈收益时,无标度网络不再对合作行为产生非凡的促进作用,其上的合作水平与规则格子上的合作水平接近[11-12]。近来,网络合作行为的涌现问题已经从理论仿真研究扩展到社会实验研究[19-24]. Carlos 等采用1229个真实社会个体构建了无标度网络和方格网。在平均收益的度量方法下,发现两个网络上的合作水平几乎相同,进而得出无标度网络并不具有对合作行为突出的促进作用[19]。那么,以上这些相互冲突的结果产生了新的研究问题:无标度网络中博弈个体的收益应该如何科学合理地度量?无标度网络对合作行为是否具有非凡的促进作用?这些问题是理论研究亟待解决的,也是本文的研究重点。
在现有研究中,无论是用累积收益还是平均收益度量个体的博弈收益,网络中每个个体均能与自己的所有邻居进行交互作用。当用累积收益进行度量时,一个个体的博弈收益为该个体与每个邻居交互作用产生的收益的加和;当用平均收益进行度量时,一个个体的博弈收益为将该个体与每个邻居交互作用产生的收益进行加和后,再除以该个体的邻居数量。因此,平均收益度量方法反映了一个隐含假设,即网络中每个个体有相同的交互作用能力,其博弈收益可用其与一个邻居交互作用所获收益的平均水平进行度量。事实上,在一个社会网络中,如果一个个体比大多数个体有着更多的连接关系,则意味着他更加擅长建立和维持社会关系。即使由于时间和精力的限制,他无法在每次博弈中和所有邻居进行交互作用,但是,与那些低连接度个体相比,他必然能够与更多的邻居进行交互作用。这是更好的社会技能,更多的资源和机会的必然结果,并在现实社会网络中普遍存在[25]。此外,现有研究发现,在平均收益度量方法下,无标度网络中高连接度个体的博弈收益反而远远小于低连接度个体的博弈收益[12]。这明显与现实世界的真实情况相违背,进而说明平均收益过度消除了高连接度个体具有的连接数量优势。鉴于此,本文提出,只要对个体的交互作用给予一定的约束,将个体的时间和精力限制清晰地体现出来,个体与邻居交互作用产生的收益的加和,即累积收益度量所采用的方法,则非常适合于度量无标度网络中个体的博弈收益,因为它反映了个体之间连接关系的差异,体现出无标度网络的典型特点。
基于以上思考,本文用仿真实验研究囚徒困境博弈和雪崩博弈在无标度网络上的动态演化。研究中提出一个新的博弈个体的交互作用模式,即博弈个体的交互作用数量有一定的限制,表达了博弈个体参与交互作用的水平,反映了现实社会中个体有限的时间和精力。在此基础上,用累积收益的方法度量个体的博弈收益,进而探讨个体博弈参与水平对无标度网络合作行为的影响,并考察无标度网络是否对合作行为有着非凡的促进作用。在以往的研究中,也有大量文献关注于对个体交互作用模式的研究。Xu Bo等[26]提出交互作用具有强度,并研究了囚徒困境博弈在在线社会网络上的动态演化,Fu Feng等[27]提出交互作用具有动态性,并研究了合作行为在动态网络上演化,Kim等[28]提出个体在与不同的邻居进行交互作用时具有差异性,并在4种不同的网络上研究了囚徒困境博弈的演化,Bausch[29]提出与邻居进行随机的交互作用,并发现了比与确定邻居进行交互作用更高的合作水平。本文则是对博弈个体的交互作用数量提出了限制,是关于个体交互作用模型的新思考和研究。
2 模型构建
2.1 个体的博弈关系
个体之间的博弈关系采用Barabási和Albert[30]的BA无标度网络模型来描述。无标度网络的生成方法为:初始网络中有m0个孤立的个体;然后,在每个时刻,一个带有m条边的新个体加入到网络中,并连接到网络中m(m≤m0)个现有个体上。新节点与网络中现有节点i进行连接的概率为:
(1)
其中N0为当前网络系统中总的节点数。经过t时间间隔后,该算法产生一个具有m0+mt个节点、mt条边的无标度网络。
个体位于无标度网络的节点上,如果博弈个体i和j之间有一条边,他们互为邻居。与以往研究假定每个个体可以和所有邻居进行博弈有所不同,本文假定每个个体在一轮博弈中最多能和W个邻居进行交互作用。W的取值表达了博弈个体参与交互作用的水平,反映了现实社会个体有限的时间和精力。那么,与博弈个体i有实际交互作用的个体称作其交互作用邻居。在这样约束条件下,连接度大于W的博弈个体在每轮博弈中只能和一部分邻居进行博弈。相应地,一个高连接度个体的邻居很可能与他没有频繁的交互作用。这反映了现实世界中个体交互作用的真实情况。下面,将W称作‘博弈参与水平’,其不同的取值代表了个体的交互作用差异。
2.2 个体的博弈行为及其演化机制
(1)个体的博弈行为
个体之间的博弈行为采用囚徒困境模型(Prisoner’s Dilemma Game,简称PDG)和雪崩模型(Snowdrift Game,简称SG)进行描述[31]。
在囚徒困境博弈中,两个博弈者同时决定合作还是背叛。合作产生收益b,但同时承担成本c(b>c>0)。二者共同合作则得到各自得到净收益R=b-c,二者共同背叛则都没有任何收益,即收益为P=0。 如果一个合作,另一个背叛,则背叛者得到最高的净收益T=b,而合作者承担了成本但没有任何收益,即净收益为S=-c。显然,无论博弈对手的决策是什么,背叛都是自身最好的选择。相应地,群体的演化稳定状态是全体背叛,不产生任何收益,尽管所有的个体都合作会产生最高的群体收益。这是收益关系T>R>P>S导致的必然结果。

根据以上描述,囚徒困境博弈和雪崩博弈的收益矩阵可用图1表示。其中,C表示合作策略,D表示背叛策略。
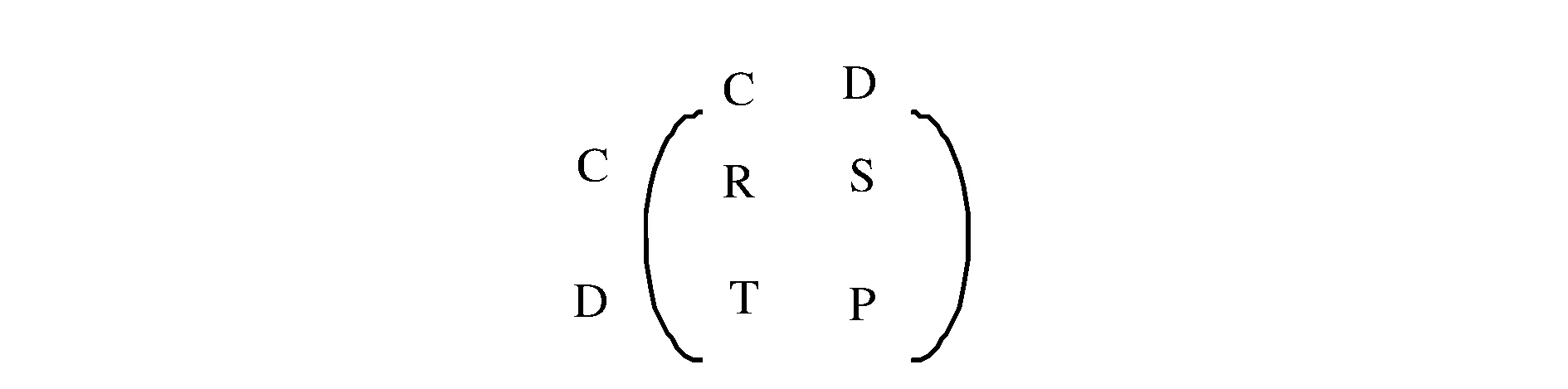
图1 博弈矩阵

(2)个体博弈行为的演化机制

(2)

pi←j=(Uj-Ui)/Dk>
(3)

3 仿真实验设计及结果
3.1 实验设计
基于以上的模型描述,本文采用Matlab编程,用Monte Carlo方法研究无标度网络上囚徒困境博弈和雪崩博弈的演化,仿真实验的总人数设定为N=1000。

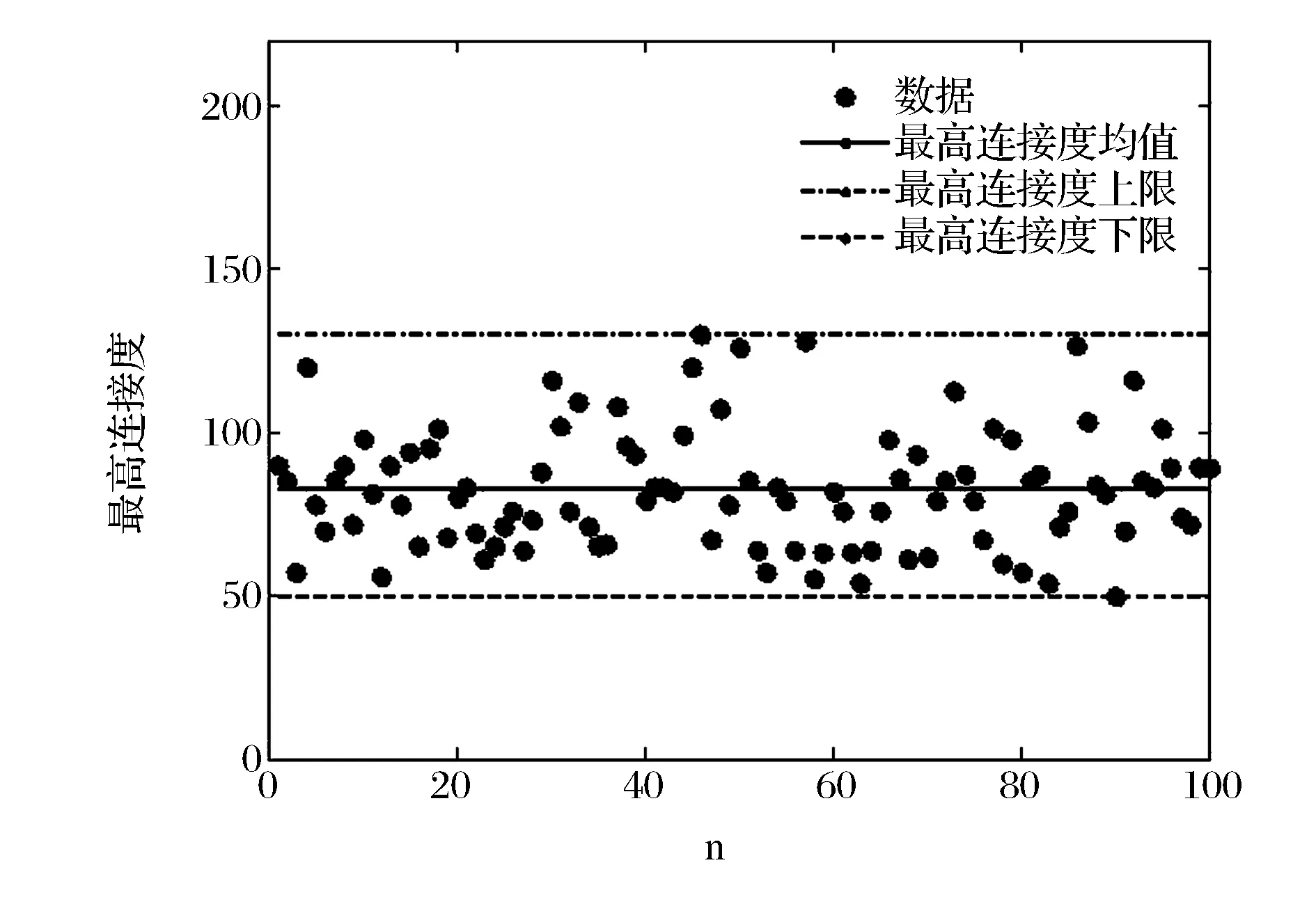
图1 1000个节点的无标度网络中,最高连接度的水平
然后,按照1.2节的模型描述,个体在每个博弈时刻t进行交互作用邻居选择,并与交互作用邻居进行博弈以获得收益。在初始时刻t=0,个体随机选择C策略或D策略作为自己初次博弈的策略。将选择C策略的个体称为合作者,将某个博弈时刻合作者在整个群体中所占的比例称为合作者密度fC(t),则有fC(t)=nC(t)/N(其中,nC(t)表示t博弈时刻群体中合作者的数量)。那么,初始时刻的合作者密度fC(0)大约为0.5。个体在获得博弈策略后,选择交互作用邻居并进行博弈,按公式(2)获得博弈收益,然后根据策略更新规则(3)进行策略调整,调整完后的策略作为自己下一次博弈时使用的策略。个体在每次博弈后对自身策略的调整使得合作者密度在下一次博弈前发生变化,形成动态演化的过程。
3.2 仿真结果

图3中的子图(a)和(b)分别给出在囚徒困境博弈(PDG)和雪崩博弈(SG)情境下,无标度网络上的合作者均衡密度PC与背叛诱惑参数b和r的关系。博弈参与水平W对合作水平的影响可以通过比较每个子图中不同颜色的曲线发现。其中,黑色十字线为将模型中的博弈参与水平W参数设置为W=1000时的结果。由于当前仿真实验的总人数N=1000,参数W=1000的设置等同于个体在交互作用时没有任何限制,可以与所有邻居进行交互作用。
由图3可以看出,对于每个固定的博弈参与水平W, 合作者均衡密度PC都随着背叛诱惑参数b和r的增大而减小。也就是说,在两种博弈情境下,背叛诱惑的程度越高,群体合作的状态越差。同时,随着博弈参与水平W的提高,合作者均衡密度PC明显增大,这意味着博弈个体积极参与交互作用对于涌现出高水平的合作状态至关重要。特别值得注意的是,当博弈参与水平增大到W=16时, 只有非常高的背叛诱惑 (b>1.7 andr>0.7) 能够使得合作者均衡密度小于个体在没有任何交互作用限制时的合作者均衡密度。这样的研究结果意味着,只要高连接度的博弈个体能与小部分邻居进行交互作用,无标度网络就能表现出非凡的促进合作的能力,进而说明无标度网络是一种非常好的适合涌现出高水平合作状态的网络形式。

(a) 囚徒困境博弈情境, b=1.5; (b) 雪崩博弈情境, r=0.5图2 合作者密度fC(t)的动态演化过程

图3 合作者均衡密度PC与背叛诱惑b和r之间的关系. (a) 囚徒困境博弈情境; (b) 雪崩博弈情境

图4 不同博弈参与水平W条件下,无标度网络上连接度为k的个体在最终演化时刻的合作者密度PC(k)。背叛诱惑取值为b=1.35和r=0.65。 (a) 囚徒困境博弈情境; (b) 雪崩博弈情境。
4 结果分析及讨论
仿真中的无标度网络有着相同的度分布,因此可以检查群体中连接度为k的个体在最终演化时刻的合作者密度PC(k),进而帮助我们理解实验结果。PC(k)采用文献[14,15]给出的计算方法:对于给定仿真参数(即给定的博弈参与水平W,背叛诱惑b或r),在群体一次演化的最后时刻,统计连接度为k的个体数量n(k)和合作者数量c(k),那么PC(k)=∑lcl(k)/∑lnl(k)(其中,l表示对于给定参数所进行的重复实验次数,l=20)。图4给出背叛诱惑b=1.35和r=0.65时,在不同博弈参与水平条件下,无标度网络上连接度为k的个体在最终演化时刻(t=5000)的合作者密度PC(k)。选择b=1.35和r=0.65进行分析的原因在于,在该背叛诱惑程度下,合作者均衡密度PC在不同博弈参与水平W下有着明显的差异(见图3),能够更好地呈现不同连接度个体在最终演化时刻的合作者密度PC(k)。
由图4可见,在囚徒困境博弈和雪崩博弈情境下,连接度为k的个体在最终演化时刻的合作者密度PC(k) 表现出相似的行为。首先,对于连接度水平较低的博弈个体(k<20),更高的博弈参与水平W必然对应着更高的PC(k);对于连接度水平较高的博弈个体(k>50),更高的博弈参与水平W对应着更多的PC(k)=1,即完全合作状态;对于连接度处于20至50的博弈个体,更高的博弈参与水平W对应着更高平均水平的PC(k)。这说明,随着博弈参与水平W的增大,个体能够进行博弈交互作用的邻居数量增多,不同连接度的个体均表现出更强的抵御背叛的能力。
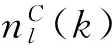
由图5可以看出,博弈参与水平W=4时,所有高连接度的博弈个体都选择背叛行为;当博弈参与水平增加到W=6 和W=8时,越来愈多高连接度的博弈个体选择合作行为;当博弈参与水平增加到W=16时,所有高连接度的博弈个体选择合作行为。这意味着,博弈参与水平W影响到了高连接度博弈个体的行为选择,在积极参与博弈的条件下,高连接度个体趋向于合作而非背叛。特别是当W=16时,连接度k高于16的博弈个体全部选择了合作行为,且几乎都获得了累积收益UC(k)=12.3。在雪崩博弈情境下,r=0.65对应着收益参数取值为β=T=1.269,R=0.769,S=0.269,P=0。那么,一个合作者可以从一个C-C博弈关系中获得收益0.769,从一个C-D博弈关系中获得收益为0.269。如果一个合作者C与W=16个邻居进行交互作用并且获得收益为12.3,即12.3/16=0.769,则说明他所有的交互作用邻居必然都是合作者C。也就是说,当博弈参与水平W足够高时,选择合作行为的较高连接度的博弈个体有非常强的能力保护自己的交互作用邻居不被背叛行为所入侵,从而使得整个群体的合作密度水平较高。
5 结语
基于对现实社会个体有限时间和精力的考虑,本文通过仿真实验分析囚徒困境博弈和雪崩博弈在无标度网络上的动态演化,进而考察博弈个体的博弈参与水平对无标度网络合作行为的影响。研究中提出一个新的博弈个体的交互作用模式,即其交互作用数量有一定的限制,表达了个体参与博弈的水平,反映了现实社会中个体有限的时间和精力。研究结果表明,在两个不同的博弈情境下,无标度网络上的群体合作水平都随着博弈个体交互作用数量的增多而提高。也就是说,博弈个体积极参与博弈表现出对无标度网络合作行为的正向影响作用。当无标度网络中高连接度的个体与大约百分之二十的邻居个体进行博弈时,群体即可达到高水平的合作状态。这说明,无标度网络非常有利于促进合作行为的演化。进一步的结果分析显示,随着博弈个体交互作用数量的增多,不同连接度的个体以不同的形式表现出更强的抵御背叛的能力;其主要原因在于,高连接度个体在积极参与博弈的条件下更趋向于合作而非背叛,进而影响到其周围的低连接度个体也选择合作行为,从而形成合作者的聚集。研究结果的启示是,社会组织中的高连接度个体如领导或核心成员,由于时间和精力的约束,往往会忽略与其他组织成员(特别是那些有着一定工作关系但却不经常接触的组织成员)的交互作用,这对于组织形成高水平的合作状态没有好处。领导或核心成员应有意识地积极与其他组织成员进行交互作用,以期获得高水平的组织合作状态。
本文基于复杂网络演化博弈理论研究了群体的合作行为。近年来,一些学者运用复杂网络演化博弈理论研究产业集群的演化问题。如张宏娟等基于集群微观异质性主体的视角,构建了传统产业集群低碳演化的模型,进行了低碳策略涌现、竞争的演化情景仿真研究[32]。吴结兵等通过对绍兴县纺织业集群30年演化历程的纵向案例研究,考察了企业适应性行为、网络化与集群发展之间的相互影响[33]。接下来,如何将复杂网络演化博弈理论更加广泛地应用于现实问题的研究,是学术界需要积极思考的问题。
[1] Nowak M A. Five rules for the evolution of cooperation[J]. Science 2006, 314(5805), 1560-1563.
[2] Nowak M A, May R M. Evolutionary games and spatial chaos[J]. Nature ,1992,359(6398):826-829.
[3] Szabó G, Toke C. Evolutionary prisoner's dilemma game on a square lattice[J]. Physical Review E, 1998, 58(1): 69-73.
[4] Szabó G, Vukov J, Szolnoki A. Phase diagrams for an evolutionary prisoner’s dilemma game on two-dimensional lattices[J]. Physical Review E, 2005, 72(4): 047107.
[5] Vukov J, Szabo G, Szalnoki A. Cooperation in the noisy case: Prisoner’s dilemma game on two types of regular random graphs[J]. Physical Review E, 2006, 73(6): 067103.
[6] Szolnoki A, Szabo G. Cooperation enhanced by inhomogeneous activity of teaching forevolutionary Prisoner’s Dilemma games[J]. Europhysics Letters, 2007,77(3):30004.
[7] PercM, Szolnoki A, SzabóG. Restricted connections among distinguished players support cooperation[J]. Physical Review E, 2008, 78(6): 066101.
[8] Hauert C, Doebeli M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game[J]. Nature, 2004, 428(6983): 643-646.
[9] Santos F C, Pacheco J M. Scale-free networks provide a unifying framework for the emergence of cooperation[J]. Physical Review Letters, 2005, 95(9): 098104.
[10] Santos F C, Pacheco J M, Lenaerts T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations[J]. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(9): 3490-3494.
[11] TomassiniM, Luthi L, Pestelacci E.Social dilemmas and cooperation in complex networks [J]. International Journal of Modern Physics C, 2007, 18 (7) : 1173-1185.
[12] Wu Zhixi, Guan Jianyue, Xu X Jinjian, et al.Evolutionary prisoner's dilemma game on Barabási-Albert scale-free networks[J]. Physica A: Statistical Mechanics and its Applications, 2007, 379(2): 672-680.
[13] Wu Yonghui, Li Xing, Zhang Zhongzhi, et al. The different cooperative behaviors on a kind of scale-free networks with identical degree sequence[J]. Chaos, Solitons & Fractals, 2013, 56: 91-95.
[14] Gómez-Gardees J, Poncela J, Floría L M, et al. Natural selection of cooperation and degree hierarchy in heterogeneous populations[J]. Journal of Theoretical Biology, 2008, 253(2): 296-301.
[15] Assenza S, Gómez-Gardees J, Latora V. Enhancement of cooperation in highly clustered scale-free networks[J]. Physical Review E, 2008, 78(1): 017101.
[16] 谢逢洁, 崔文田, 孙笑明. 无标度网络的群聚性对合作行为的影响[J]. 系统工程学报, 2010, 25(2): 152-158.
[17] 林海, 吴晨旭. 基于遗传算法的重复囚徒困境博弈策略在复杂网络中的演化[J]. 物理学报, 2007, 56(8): 4313-4318.
[18] 陈亮. 无标度网络中的公共物品博弈[J]. 苏州大学学报(自然科学版), 2009, 25(4): 43-47.
[19] Gracia-Lázaro C, Ferrer A, Ruiz G, et al. Heterogeneous networks do not promote cooperation when humans play a Prisoner’s Dilemma[J]. Proceedings of the National Academy of Sciences, 2012, 109(32): 12922-12926.
[21] Traulsen A, Semmann D, Sommerfeld R D, et al. Human strategy updating in evolutionary games[J]. Proceedings of the National Academy of Sciences, 2010, 107(7): 2962-2966.
[23] Rand D G, Nowak M A, Fowler J H, et al. Static network structure can stabilize human cooperation[J]. Proceedings of the National Academy of Sciences, 2014, 111(48): 17093-17098.
[24] Gracia-Lázaro C, Cuesta J A, Sánchez A, et al. Human behavior in prisoner's dilemma experiments suppresses network reciprocity[J]. Scientific Reports, 2012(2).
[25] Luthi L, Tomassini M, Pestelacci E. Evolutionary games on networks and payoff invariance under replicator dynamics[J]. Biosystems, 2009, 96(3): 213-222.
[26] Xu Bo, Liu Lu, You Weijia. Importance of tie strengths in the prisoner's dilemma game on social networks[J]. Physics Letters A, 2011, 375(24): 2269-2273.
[27] Fu Feng,Wu Te,Wang Long.Partner switching stabilizes cooperation in coevolutionary prisoner’s dilemma[J]. Physical Review E, 2009,79(2):036101-1-036101-7.
[28] Kim J W. A tag-based evolutionary prisoner's dilemma game on networks with different topologies[J]. Journal of Artificial Societies and Social Simulation, 2010, 13(3):1-17.
[29] Bausch A W.Stochastic interactions increase cooperation in a spatial Prisoner's Dilemma[J]. Complexity, 2014,21(2):82-92.
[30] Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.
[31] Doebeli M, Hauert C. Models of cooperation based on the Prisoner's Dilemma and the Snowdrift game[J]. Ecology Letters, 2005, 8(7): 748-766.
[32] 张宏娟, 范如国. 基于复杂网络演化博弈的传统产业集群低碳演化模型研究[J]. 中国管理科学, 2014, 22(12): 41-47.
[33] 吴结兵, 郭斌. 企业适应性行为, 网络化与产业集群的共同演化——绍兴县纺织业集群发展的纵向案例研究[J]. 管理世界, 2010,(2): 141-155.
The Effect of Player Participation on the Evolution of Cooperative Behaviors in Scale-free Networks
XIE Feng-jie1, WU Xiao-ping1,CUI Wen-tian2,CHEN Zi-feng1
(1.College of Economics and Management, Xi’an University of Posts and Telecommunications, Xi’an 710061, China; 2.School of Management, Xi’an Jiaotong University, Xi’an 710049, China)
The evolution of cooperation in prisoner’s dilemma game (PDG) and snow game (SG) on scale-free networks has been explored in this study. One-shot two-person game is played between neighbors on scale-free networks. Players have two possible strategies, cooperate or defect, and the strategies evolve according to the update rule of limited population analogue of replicator dynamics. Different from previous studies in which a player can interact with all his neighbors in every round of the game, this work proposes a new interaction pattern of players. A player can interact with at mostWneighborsineveryroundofthegame,whoarenamedasinteracting-neighbors.ThevalueofWreflectsthelimitedtimeandenergyofplayers,andthusdescribesthelimitedinteractionlevelofplayersinanetworkedPDGandSG.Resultsindicatethatahigh-levelofcooperationinPDGandSGcanbeachievedonscale-freenetworksaslongashigh-connectivityplayersinteractwithasmallfractionoftheirneighbors,andtheinteractionlevelsofplayershavesignificantpositiveeffectsoncooperation.Theseresultssuggestthatevenifindividualsinrealworldhavelimitedtimeandenergytointeractwitheachother,theycouldstillpreservecooperationbecausetheirinteractionsarerootedinactualscale-freenetworks.Moreover,high-connectivityindividualssuchasleadersordirectorsinanorganization,whogenerallypreferinteractingwitheachotherinrealworld,playanimportantroleintheevolutionofcooperation.Currentworkprovidesanewinteractionmechanisminnetworkedgameandcontributestounderstandingtheemergenceofcooperationinrealsociety.
scale-free networks; prisoner’s dilemma game; snowdrift game; cooperative behavior; game participation level
1003-207(2017)05-0116-09
10.16381/j.cnki.issn1003-207x.2017.05.014
2015-08-14;
2016-03-21
国家自然科学基金资助项目(71072128);国家社会科学基金资助项目(15BGL014); 教育部人文社科基金资助项目(12YJCZH226);西安邮电大学西邮新星团队基金(XYXX201406)
谢逢洁(1974-), 女(汉族), 重庆人,西安邮电大学经济与管理学院副教授,博士, 研究方向:复杂网络理论及其应用,E-mail: fengjie_xie@163.com.
O157.5;N941.4
A
