基于病毒协同遗传算法的自动化立体仓库货位优化模型
2017-06-01李鹏飞
李鹏飞,马 航
(西安邮电大学经济与管理学院,陕西 西安 710121)
基于病毒协同遗传算法的自动化立体仓库货位优化模型
李鹏飞,马 航
(西安邮电大学经济与管理学院,陕西 西安 710121)
自动化立体仓库是一个错综复杂的存储系统,货位优化问题直接影响自动化立体仓库的工作效率。针对自动化立体仓库的货位选择问题,本文提出以出入库效率和货架稳定性为优化因素的货位优化模型,并采取病毒协同遗传算法对优化模型进行仿真。最后对仿真结果及货位优化前,病毒协同遗传算法优化后,传统遗传算法优化后三者的对比结果进行分析,结果说明病毒协同遗传算法(VEGA)能有效实现自动化立体仓库货位优化,是提高货物出入库效率和货架的稳定性的一种有效方法。
自动化立体仓库;货位优化;病毒协同遗传算法
1 引言
近些年随着现代物流企业对仓储的货位调度水平要求越来越高,自动化立体仓库的货位优化问题成为关注的焦点。自动化立体仓库是现代物流、仓储技术和计算机技术的高集成产物,它不仅可以实现货物的自动化并行存取,而且可以提高货物存取的效率和准确性。
国外研究有:Lam等[1]提出货位优化问题是仓储货位管理的核心问题之一。Kubota等[2]提出了基于病毒进化理论的遗传算法VEGA(Virus co-evolution genetic algorithm),并成功将VEGA应用于旅行商问题、背包问题、自组织系统的调度问题等。Koster等[3]梳理了手工货位分配作业流程设计与控制的决策方案,包括货位布局设计、货位分配方法、分区等;Ma Yongjie等[4]提出了利用遗传算法解决仓储调度问题,并指出传感遗传算法的局限性。Kim等[5]将储位再分配问题定义为一个多物料流问题,以最小化运输和库存的成本。Zu Qiaohong等[6]提出一种运用混合遗传算法的解决货位优化问题,遗传算法是一种模拟自然界生物进化的自搜索方法,该方法在解决最优化问题具有较大优势,但是该种混合遗传算法在解决货位优化问题时会存在局部收敛的问题。
国内研究有:在货物进行出入库操作时,选择合适的货位可以提高货物出入库的效率,并减少出入库的成本。当货物存放不合适的货位时,就需要对货物进行货位调整,实现货位的优化。目前针对货位优化问题的研究有很多,薛桂香[7]提出了一种网格任务调度模型,用以解决自动化仓储调度问题,该种方法虽然解决了货物调度的问题,但是并未使货位优化达到最优。邓爱民等[8]以医药为例提出一种基于时间的货位优化多目标模型,结果表明优化前后数据记录能有效进入仓储自动管理环节,可以降低仓库管理成本。鄂晓征等[9]根据汽车零配件仓储的特点,提出了基于遗传算法的智能仓储货位调度方法,结果表明零部件的出库效率有所改善,但是遗传算法自身具有局限性,有时不能较好的收敛。王进业和宋宇博[10]分析了旁通式自动化立体仓库的工作特点,将遗传算法用于模型的路径优化,仿真结果显示这种方法是可行的、有效的。
从上面文献综述可以看出,目前很多仓库货位优化的研究只考虑货物重量和货物分类摆放问题,但对于货物出入库效率和货架稳定性考虑的较少。针对这些问题,考虑传统遗传算法不能实现全方位优化,存在局部优化缺陷,本文提出以出入库效率和货架稳定性为优化因素的病毒协同遗传算法对货位优化问题进行研究。
2 构建货位优化多目标优化数学模型
2.1 模型假设
根据自动化立体仓库在货物调度时遇到的问题和应该遵循的效率原则和重力原则[11-12],本文对模型的部分参数进行假设。
假设自动化立体仓库共有货架a排,每排货架有货位b层c列,其中距离地面最近的为第1层,距离出入口最近的为第1列,距离货物进出口最近的为第1排,每个货位的长宽高均为L(假设L=1即模型中取货位长宽高为1单位大小),模型中不用考虑巷道之间的距离,故可以将这个模型简单理解为一个三维立体空间的点集,也就是处于第x排第y层第z列的货位可以定义坐标为(x,y,z),其中xyz均为正整数[13]。
同时假设仓库中可以存放N种不同的货物,并且每种货物只允许存放在一个货位中,不允许同一货位中存放不同类型的货物。每个货物有其基本信息,货物的重量用M表示,货物的周转率用P表示,其中M的单位是kg,P的单位是频次即某货物在一定时间内的周转次数,本文用P次/月表示。
根据以上描述,假设总结如下:
(1)立体仓库模型的整体布局被定义为一个标准的空间长方体的点集合(x,y,z),暂以理想模型考虑。
(2)货物的种类已知,相同种类的物品可以合并托盘放在同一货架中(大小不得超过货位容量),而且货物重量要均匀分布。
(3)考虑到曲线运动计算的复杂性,本文货物在进出库时是按照直线运动。
(4)本模型是一个三围立体的空间模型,为简单起见,假设货位的长宽高均为单位1,货位的体积为1m3。
(5)堆垛机存取货物的时间暂时不记,仅考虑传送带和堆垛机的运行速度。
(6)所有货架的托盘尺寸都是相同的,但是托盘上货物重量不一定相同。
(7)每个巷道只有一台堆垛机。
(8)传送带只沿着X轴方向水平运动,运行速度是Vx;堆垛机只在Z轴方向上做水平移动速度和垂直移动,运行速度分别为Vz和Vy,单位均为米/每秒。
2.2 模型分析建立过程
根据模型的假设条件描述,本文模型主要优化目标是提高出入库的效率,降低货位重心并提高货架稳定性[14]。模型分析如下。
2.2.1 出入库效率分析
为了提高出入库的效率,就必须考虑出入库距离和时间两个因素,若假设条件中Vx=Vy=Vz,即传送带的搬运速度和堆垛机的水平和垂直速度相同,距离和时间就是正比关系,无论是距离最短还是时间最短都是一样的;若假设中的Vx≠Vy≠Vz,即传送带的搬运速度和堆垛机的水平垂直速度不同,则在判断出入库效率的时候就必须主要考虑时间因素,因为时间是衡量效率的标准之一。假设立体货架某货位的坐标是(x,y,z),货物进出口坐标记为原点(0,0,0),由于传送带和堆垛机的移动不能按照距离最短的直线移动。根据提高仓库进出货效率的就近原则和周转率大小原则,即使所有货物的出入库时间和周转率频率的乘积之和最小。其中,Pxyz为货位在货位(x,y,z)处的周转率,建立数学模型的目标函数f1(x,y,z)如公式(1)所示:
(1)
2.2.2 货架稳定性分析
任何一个仓库的立体货架,它的承重能力都是有限的,所以在存放货物的时候,要想保持货架有良好的稳定性就要使货架的整体重心最低。也就是说要将较重的货物放在货架的底层,将较轻的货物放在立体货架的上层。在实际问题中,立体货架的稳定性主要和重心有关,其重心越低,货架的稳定性就越好。因此,按照上轻下重的摆放原则可以减轻货架的重心,从而达到提高货架稳定性的效果。
在本文模型当中,假设货位(x,y,z)处货物的质量为Mxyz,根据货架承重遵循“上轻下重”重心最低的存储原则,即每个托盘上的货物质量与其所在层的乘积之和最小,此时货架的稳定性最好,由此可以建立数学模型的目标函数如公式(2)所示:
(2)
因此,根据货位优化的目标可以得到多目标数学模型,如公式(3)所示:
(2-3)
模型中变量说明:
Pxyz为货位在货位(x,y,z)处的周转率,即根据数据可以得的已知变量;
Mxyz为货架第x排第y层第z列货物的质量,为已知变量;
L为货位的单位长度,模型中视为1,为已知变量。
2.3 问题转化
在多目标优化问题求解时需要综合考虑各个目标,使得各个目标函数的函数值都在给所定的区域上尽可能地向着求解的方向靠拢或接近,而达到多个目标的最优化。本文采用病毒协同遗传算法,结合权重法,将算法进化分解成若干群体,各子群体在不同的权重系数进行不同方向上的搜索获得妥协解[15]。
给每个目标函数fi(x)(i=1,2,…,q)各自赋予权重wi(i=1,2…,q),此处权重wi表是各子目标对fi(x)的重要程度。那么,多目标优化问题可以表示为,如公式(4)所示:
(4)

根据上文分析,立体仓库货位优化问题是由出入库效率和货架稳定性两个目标组成的多目标优化问题,通过公式(4)可将多目标优化问题转化为单目标优化问题进行求解,可描述为公式(5):
F(x,y,z)=ω1f1(x,y,z)+ω2f2(x,y,z)
(5)
2.4 权重的确定
确定权重的方法包括德尔菲法、AHP层次分析法和熵值确定权重法等,其中最常用的是AHP层次分析法,而本文将德尔菲法和AHP层次分析法相结合,步骤如下:
(1)货位优化的目的是为了降低库存成本并提高出入库效率。根据实际经验可以得出,对于出入库效率和货架稳定性两个因素,前者要比后者重要,根据系统工程的标度定义aij(如表1所示),本文选取1、3、5、7、9标度。

表1 判断矩阵标度定义
(2)根据德尔菲法的基本原理,本文邀请12位专家组成专家小组,并对标度的选择进行三次投票,投票结果如表2所示。

表2 德尔菲法投票结果


表3 一致性检验

综上所述,变型可得货位优化模型为,如公式(2-6)所示:

(6)
3 病毒协同遗传算法
3.1 病毒协同遗传算法的原理
病毒协同遗传算法基本思想是优秀基因的识别和优秀基因的增长,其基本操作步骤主要是首先初始化种群,将种群中的每一个个体作为一个基因,经过选择、交叉和感染操作过程,获得适应度函数最优解[16-17]。病毒协同遗传算法的基本流程如图1所示。

图1 病毒协同遗传算法基本流程图
3.2 病毒个体的感染操作
病毒个体的感染包括如下三个操作:
(1)感染(Infection)操作
主个体中的染色体相应的基因被病毒染色体感染,进化产生新的病毒染色体因,从而产生进化解。如果在主个体在受到病毒个体以Pinfect概率感染后适应度值变小了,则丢弃感染前的主个体,选择感染后的主个体,如图2所示。
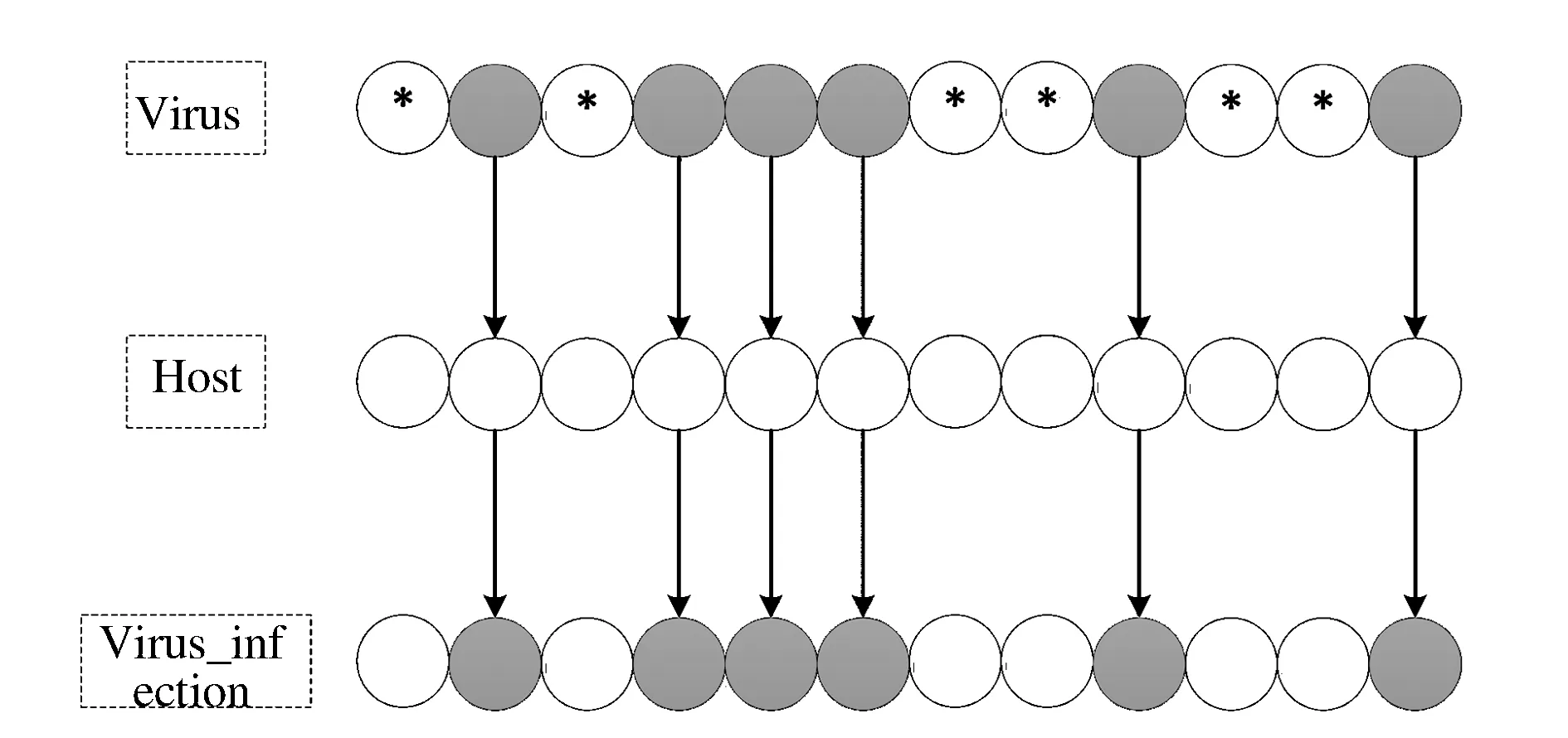
图2 感染操作
(2)复制(Copy)操作
复制操作一般存在两种情况,一种是初始病毒复制,另一种是非初始病毒复制。初始病毒复制是通过“无感染能力”的病毒个体的复制操作产生新的病毒个体,如图3a所示;而非初始病毒复制则是病毒个体从主个体获取基因改变自己的基因,从而产生新的病毒个体,如图3b所示。

图3a 初始病毒复制操作

图3b 非初始病毒复制操作
(3)删减(Cut)操作
病毒染色体每个基因以概率Pcut用通配符进行替换,用以删减个体部分基因,减少病毒个体的长度,降低进化的计算能力,如图4所示。

图4 删减操作
3.3 病毒协同遗传算法实现
病毒协同遗传算法实现步骤如下:
(1)编码
模型采用实数编码方式,因为实数编码方式的染色体的空间拓扑结构和它的表现型的空间拓扑结构是一致的。编码方式如下:
①条染色体代表一种货位分配方式。
②一条染色体可以分为N段,每段代表一个基因,每个基因代表一个货位的位置(x,y,z),每个基因都对应一个货物的编号,其中N为这个染色体中货物的个数。
③每段基因都是由三位整数表示,其中百位代表x的值,十位代表y的值,个位代表z的值。
假设分拣缓存区有4个货物要进行入库,其中1号货物要放在(1,2,3)的位置上;2号货物要放在(2,2,3)的位置上;3号货物要放在(3,2,4)的位置上;4号货物要放在(4,4,4)的位置上。那么“123”、“223”、“324”、“444”分别表示一个染色体的基因,这时候染色体就形成了一个解“123223324444”,表示一种货位分配的方式。如图5所示。

图5 编码方式
(2)初始化种群
在初始化种群的时候,可先设置种群规模M,然后根据个体长度为N,采用随机配的方法产生M个这样的个体,这就完成了种群规模为M的初始化工作。
(3)选择操作
在模型中选用轮盘赌选择(Roulette wheel selection)方法,它是比例选择中较为常用的方法,其基本思想是:个体被选中的概率取决于该个体的相对适应度。而相对适应度如公式(7)所示:
(7)

(4)交叉操作
交叉选择的是实属交叉,实数交叉又分为离散交叉和算术交叉,本文使用的是离散交叉,离散交叉是在两个父代个体的编码向量都选取0.5的概率进行交换,从而生产新的向量。这种两两配对的方式是病毒协同算法进行感染操作的第一步。假如两个父代个体的n维向量如公式(8)所示:
(8)
则交叉随机选择第k个以后的分量,生成两个新的个体向量如公式(9)所示:
(3)
(5)病毒个体感染操作
利用病毒染色体基因替换主染色体中相应的模式基因,从而产生新的主个体。每个病毒个体以一定概率Pinfect感染每个主个体,如果主个体感染后的适应度值减小了,则用感染后的主个体替换感染前的主个体。一个个体的适应度值越小,它被遗传到下一代种群中的概率也就越大,遗传算法种群进化的过程中,基本上都是根据适应度函数作为优胜劣汰的标准。
4 仿真与结果分析
本文采用MATLAB7.0对模型进行仿真,数据收集如下:
(1)仓库基本参数(见表4)

表4 仓储基本参数信息
(2)货物基本信息收集
货物的基本信息如表5所示,本文选择17件货物作为仿真数据,其中货物的重量是货物分拣后托盘的重量。而货物的周转率是根据以往数据算出的,即平均每个月该货物进出仓库的次数。

表5 货物基本信息
(3)遗传算法参数选取
遗传算法参数的选取会影响最终输出结果的优劣,因此在进行仿真的时候要对参数进行测验。但是考虑仿真结果客观性,程序中初步选取的遗传算法参数如表6所示。

表6 遗传算法参数选取
利用收集的仿真数据,通过MATLAB仿真实验得出结果如图6所示。从图中可以看出VEGA适应度值随着迭代次数逐渐降低,相比GA较早出现收敛,而且VEGA曲线几乎一直低于GA曲线。可见,VEGA算法相比传统的GA算法在解决货位优化问题上具有较好的收敛性,同时也具有较快的收敛速度,避免了传统遗传算法陷入局部最优解的缺陷,从而提高了自动化立体仓库的货位优化水平。

图6 VEGA与GA算法MATLAB仿真结果
病毒协同遗传算法与传统遗传算法的货位优化的数据结果如表7所示,结果分析如图7与图8所示,包括货位优化前、GA优化后和VEGA优化后的数据结果。
(1)从图7可以看出,优化前较GA和VEGA优化后的货物出入库距离更长,说明通过两种算法优化后的货位距离出口更近;比较GA与VEGA的算法结果,VEGA优化后的货物出入库距离较短。
(2)从图8可以看出,优化前较GA和VEGA优化后的货物出入库时间更长,说明通过两种算法优化后的货位出入库时间更短;比较GA与VEGA的算法结果, VEGA优化后的货物出入库时间较短。

表7 VEGA与GA仿真数据结果

图7 优化结果数据对比分析(一)

图8 优化结果数据对比分析(二)
(3)稳定性数值越小说明货架稳定性越好,从图9可以看出通过GA和VEGA优化后的货架稳定性较优化前更稳定,而VEGA相比GA优化后的稳定性系数更低一些,说明通过VEGA优化后的货架稳定性更好。
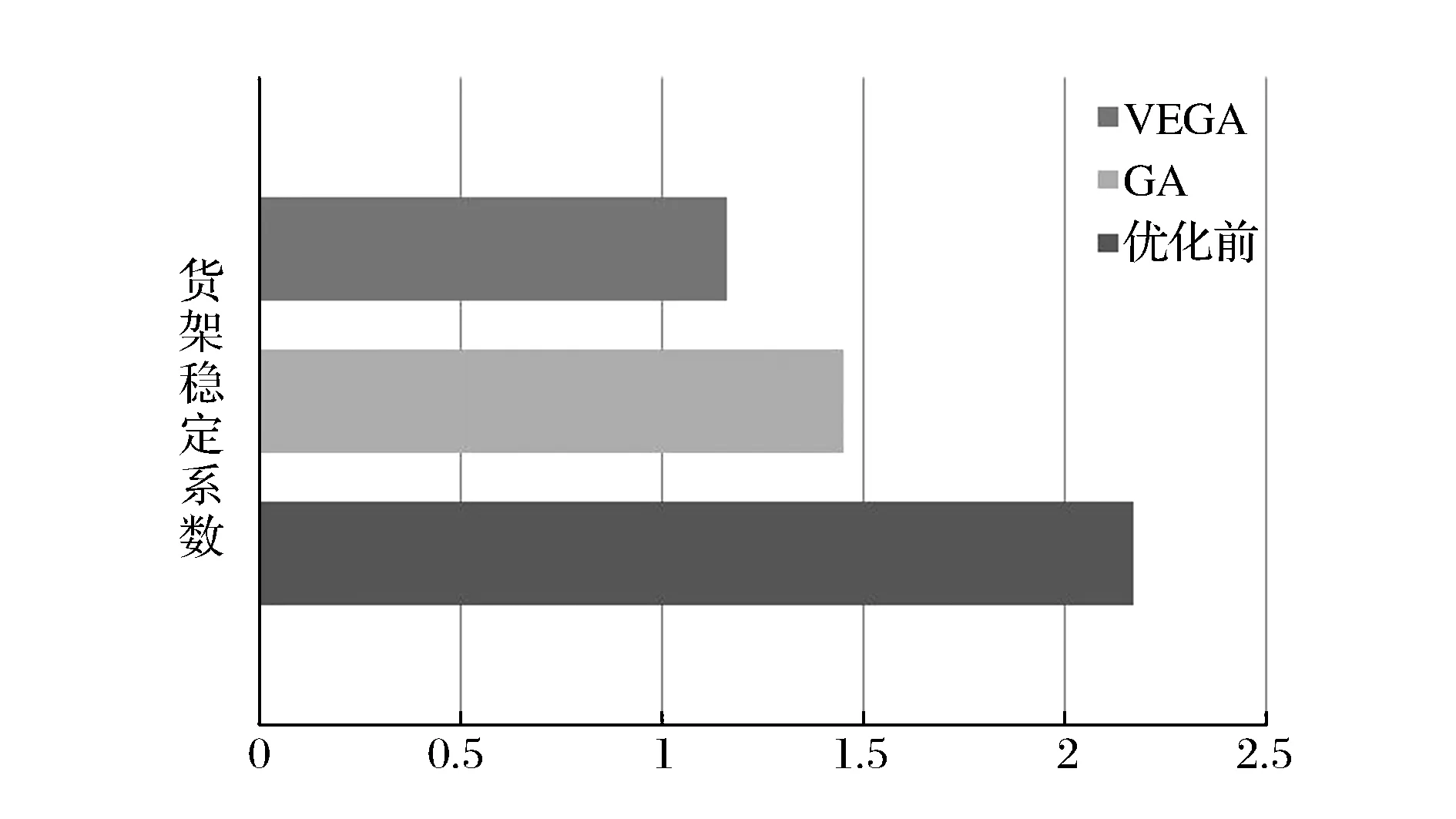
图9 优化结果数据对比分析(三)
通过病毒协同遗传算法与传统的遗传算法在货物出入库距离、货物出入库时间、货架稳定性等方面的对比,可以发现经过优化后,货物的摆放更加规范,表明病毒协同遗传算法能有效解决货位优化问题,并验证了提出方法的有效性。
5 结语
货位优化问题是仓储货位管理的核心问题之一,本文得出以下三个结论:
(1)病毒协同遗传算法相比传统的遗传算法具有较好的收敛性,拥有较快的收敛速度,避免了传统遗传算法陷入局部最优解的缺陷,从而提高了自动化立体仓库的货位优化水平。
(2)病毒协同遗传算法优化后,提高自动化立体仓库的货物出入库效率。能够缩短货物出入库距离并且减少货位入库时间。
(3)病毒协同遗传算法稳定性系数较低,能够更好的提高货架稳定性。
综上所得,通过病毒协同遗传算法能够优化自动化立体仓库货位,提高出入库效率和货架稳定性。
[1] Lam C H Y, Choy K L, Chung S H.Framework to measure the performance of warehouse operations efficiency [C]. Proceedings of the 8th International Conference on Industrial Informatics,Oskar,Japan,July 13-16,2010.
[2] Kubota N, Arakawa T, Fukuda T,et al. Fuzzy manufacturing scheduling by virus-evolutionary genet- ic algorithm in selforganizing manufacturing system[C]//Proceedings of the 6th international conference on Fuzzy systems. Barcelona:IEEE,July 5,1997:1283-1288.
[3] de Koster R,Le-Duc T,Roodbergen K J.Design and control of warehouse order picking:A literature review [J].European Journal of Operational Research,2007,18 (12):48-50.
[4] Ma Yongjie, Yun Wenxia, Hou Wenjing. The research progress of genetic algorthm in the large warehouse system [C]// Proceedings of the 2010 Conferences on Optoelectronics and Image Processing,Barcelona:IEEE,November 11-12,2010:616-620.
[5] Kim K H,Park K T.Dynamic space allocation for temporary storage [J].International Journal of Systems Science,2003,34(1):11-20.
[6] Zu Qiaohong, Cao Mengmeng. Slotting optimization of warehouse based on hybrid genetic algorithm[C]// Proceedings of the 6th International Conference on Pervasive Computing and Applications,Bacelona:IEEE,October 26-28,2011:19-21.
[7] 薛桂香.基于智能优化算法的网格任务调度策略研究[D].天津:天津大学,2008.
[8] 邓爱民,蔡佳,毛浪. 基于时间的自动化立体仓库货位优化模型研究[J]. 中国管理科学,2013,21(6):107-112.
[9] 鄂晓征,祖巧红,曹萌萌.基于遗传算法的汽车零件自动化仓储货位优化[J].系统仿真学报,2013,25(3):430-435+444.
[10] 王进业,宋宇博.旁通式自动化立体仓库拣选作业和出口选择的组合优化[J].河北科技大学学报,2015, 36(1):36-40.
[11] 张雄飞,柳少军.一种改进遗传算法及在多目标优化中的应用[J]. 系统管理学报,2007,16(3):315-319.
[12] 张群,颜瑞.基于改进模糊遗传算法的混合车辆路径问题[J]. 中国管理科学,2012,20(2):121-128.
[13] 常发亮,刘增晓,辛征,等.自动化立体仓库拣选作业路径优化问题研究[J]. 系统工程理论与实践, 2007,27(2):139-143.
[14] 曹浪财,罗键. 可视化自动仓储系统设计与货位优化[J]. 厦门大学学报(自然科学版),2012,51(1):46-50.
[15] 孙艳丰. 基于GATS混合策略的多目标优化算法[J]. 管理工程学报,2000,14(4): 4-7.
[16] 胡仕成,徐晓飞,李向阳. 项目优化调度的病毒协同进化遗传算法[J]. 软件学报,2004,15(1):49-57.
[17] 戢守峰,李峰,董云龙,等. 基于遗传算法的三级逆向物流网络设计模型研究[J].中国管理科学,2007, 15(6):86-91.
Virus Based on Cooperative Genetic Algorithm Automated Warehouse Space Optimization Model
LI Peng-fei, MA Hang
(Xi'an University of Posts & Telecommunications,School of Econonnics and Management, Xi'an 710061,China)
Automated warehouse is an intricate system of storage, and slotting optimization problems directly affect the efficiency of the Automated Warehouse. To solve the dilemma of location selection of automatic stereo warehouse, a Slotting Optimization model which take the out of storage efficiency and shelf stability of storage as its optimization factors is proposed, the Multi-objective mathematical model of Slotting Optimization is established. According to the actual conditions of Automated Warehouse, with the help of Strategy Set Transformation, Delphi method and the Analytic Hierarchy Process(AHP) are used to determine the weight. And virus combined with genetic algorithm is taken to simulate the optimization model. In the MATLAB software environment, the Multi-objective genetic algorithm for virus is utilized to calculate the model solution. Finally, the results comparison among the simulation of the data before Slotting Optimization, the data after virus combined with genetic algorithm and the data after traditional genetic algorithm indicates that Virus Cooperative Genetic Algorithm(VEGA) can effectively optimize the automation stereoscopic warehouse slotting. It is also a kind of effective way to improve the efficiency of goods out of storage and stability of shelf.
automated warehouse; mization of the goods location; virus cooperative genetic algorithm
1003-207(2017)05-0070-08
10.16381/j.cnki.issn1003-207x.2017.05.009
2016-01-11;
2016-05-26
陕西省科技厅科研项目(2014K05-62);陕西省教育厅科研项目(14JK1647);陕西省社科基金重大项目(2016ZDA10);西安邮电大学西邮新星团队资助
李鹏飞(1975-),男(汉族),陕西户县人,西安邮电大学经济与管理学院,博士,教授,研究方向:邮政及物流信息化,E-mail:lpf@xupt.edu.cn.
F273;C935
A
