公益基金投资决策综合分析模型

刘臣 王育清 韩林

摘 要：投资对象的选取以及投资金额的确定是公益基金投资决策的重要环节，针对公益基金投资决策依据标准不足问题，文中提出基于层次分析和动态规划相结合的决策分析模型。基于美国国家教育统计中心数据，文中首先采用层次分析法，经矩阵分析运算，将需要投资的对象进行排名。然后利用效益函数，保证投资总金额一定的条件下，采用动态规划的方法，确定对各投资对象的投资金额，从而使得潜在收益最大化。研究表明，该方法具有一定的实用性，能够有效解决公益基金的投资决策问题。

关键词：投资决策；层次分析；矩阵分析；动态规划；投资效益

中图分类号：N 202 文献标识码：A 文章编号：1672-7312（2017）02-0145-05

Abstract：Choosing investor and determining investment amount are the important elements of the investment decision about public welfare fund.According to the deficiency of the standard to determining the method of public welfare fund investment，this paper proposes a decision making analysis model based on the combination of analytical hierarchy process and dynamic programming.Based on the data of American national education statistics center，this paper first adopts AHP through the operation of matrix analysis to rank the objects that need fund investment.Then it uses efficiency function and the method of dynamic programming to determine the amount of investment to each investee under the condition that the total amount of investment does not change in order to make the potential benefits maximum.This method is practical and can solve the problem of the investment decision about public welfare fund.

Key words：investment decisions；hierarchical analysis；Matrix analysis；dynamic programming；investment efficiency

公益基金投资与一般投资具有一定的相似性，同时又有着很大的不同。虽然都需在考虑一定效益的情况下确定投资目标，但相比一般投资而言，公益基金的投资不用考虑投资风险等因素，研究其模型必然不像风险投资那样复杂，但公益基金的投资收益更加难以测评，因此需要运用不同的模型来研究公益基金的投资决策。以往公益基金投资对象的选取、甚至投资金额的多少更多地依赖过去经验或者人们的主观评价。社会救助政策方案规划必须着眼于按需分配和公平，努力使社会福利最大化[1]，因此从定量的角度给出一个客观的分析模型很有价值，能够使得公益基金的投资方向更加明确化，也能够使得投资更合理，带来更大的潜在社会价值。对此，文中结合层次分析

[2-3]和动态规划[4-5]2种方法，给出考虑潜在投资收益的公益基金投资决策综合分析模型，并用实例加以验证。

1 问题的提出

现以美国Goodgrant Foundation投资为例，其捐赠总金额为1亿美元，以美国国家教育统计中心已有的2 000多所专科及以上学校的机构性能统计数据为依据，从中选出一定数量的学校进行投资，使得投资回报最大。据此我们提出以下模型，从而求出投资的最大收益以及每所学校的投资额。在投资过程中假设投资总金额为定值S，需要投资的对象为N，从中要选出M个对象m1，m2，…mm进行投资，依据往年投资回报函数确定给每个对象的投资金额s1，s2，…，sm，当给每个对象投资不同的金额时，投资回报不同为gij，i代表投资的对象，j代表投资的金额，以期潜在投资回报G最大。

依据经验需要按照不同的指标，对每个对象进行评价，依据分值的多少给出投资对象的排名。层次分析方法可以有效解决该问题[6-7]，层次分析法能够将定性与定量结合，将人的主观判断用數量形式处理，将复杂问题分解成各个组成因素，又将这些因素按支配关系分组，形成递阶层次；各层次中诸因素两两进行比较，从而确定决策对象相对重要性总的排序。得到排序之后确定每个投资对象的投资金额，使得总投资金额一定而且总效益最大，此时可以利用动态规划方法[8]，该方法考虑多级决策过程的最优策略的性质：不论初始状态和初始决策如何，其余的决策对于由初始决策所形成的状态来说，必定也是一个最优策略。这个原理可以归结为一个基本的递推公式，属于多阶段决策。我们将综合运用2种模型对公益基金投资决策问题进行解决。

2 决策对象重要性排名

2.1 层次分析模型

通过层次分析法可以得到决策对象的重要性排名。采用该方法时，首先构建层次结构模型，通过模型的构建将复杂系统的评价决策思维过程量化。A，B，C等3层依次为目标层、准则层、方案层[9]。

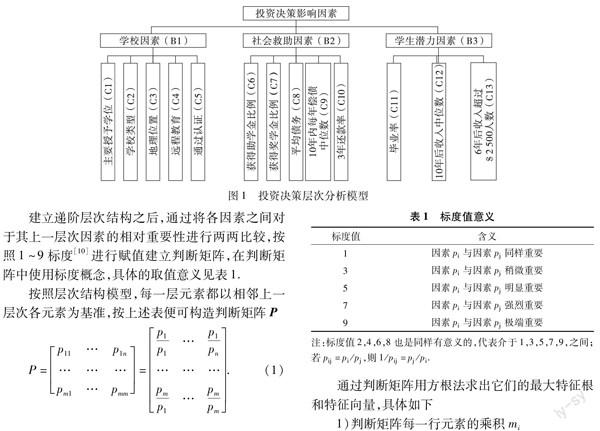
针对研究问题本身，依据已有数据，将投资决策分为3类基本因素，分别是学校因素、社会救助因素、学生潜力因素。基本因素又可进一步细分为多向评价指标，包括主要授予学位、学校类型、地理位置、远程教育、通过认证、获得助学金比例、获得奖学金比例、平均债务、10年内每年偿债中位数、3年还款率、毕业率、10年后收入中位数、6年后收入超过$2 500人数，具体划分如图1所示。

建立递阶层次结构之后，通过将各因素之间对于其上一层次因素的相对重要性进行两两比较，按照1～9标度[10]进行赋值建立判断矩阵，在判断矩阵中使用标度概念，具体的取值意义见表1.

2.2 各因素权重的确定

根据所建的递阶层次模型建立B层各元素相对于总目标A层的两两判断矩阵（见表2）。

2.3 综合排名

权重确定之后（见表6）便可得到各学校投资决策顺序的先后排名，部分学校排名（见表7）。

3 投资方案确定

3.1 动态规划理论分析

运用动态规划原理，依据投资收益最大化原则，可以得到投资金额一定时，应该采取怎样的投资方案使得总收益最大。

4 结 语

文中提出将层次分析与动态规划方法相结合解决公益基金投资决策问题，使得投资人员结合已经收集到的数据，能够运用科学的方法，选择决策对象以及投资额，并预测投资的最大收益，从而给出合理的投资方案。运用层次分析这一多目标多标准的决策方法，通过两两比较，确定出对象的优先顺序，接着运用动态规划方法，将每一个学校的投资作为一个阶段，使得全局投资收益最优。这种方法能够影响的目标众多，不同的方案对每个对象的影响不同，产生的效果不同。将复杂的问题分解变为较为简单的问题，使得主观考量的问题有了客观的依据。

该方法虽然可以解决投资优化问题，但也存在一些不足：首先在层次分析中各因素之间权重的比较存在一定的人为因素；另外关于投资收益函数是依据经验进行拟合的，而并不是公益基金投资统计研究出来的结果，在投资学校的数量，以及金额的分配上也是实验过程中设定的，因此该方案不是全局最优，只是一个局部最优。而关于这一问题的解决都将成为我们今后研究的目标。

参考文献：

[1]GUO T.Research on policy formulation in social aid from visual angle of welfare economics[C]//Proceedings of the Remote Sensing，Environment and Transportation Engineering（RSETE），2011 International Conference on，F，2011.

[2]Podvezko V.Application of AHP technique[J].Journal of Business Economics & Management，2009，10（2）：181-189.

[3]ZHU Y.Determination of weight value by AHP[J].Journal of Northern Jiaotong University，1999（2）.

[4]李 端，钱富才，李 力，等.动态规划问题研究 [J].系统工程理论与实践，2007，27（8）：56-64.

[5]Bertsekas D P，

Bertsekas D P，Bertsekas D P，et al.Dynamic programming and optimal control[M].MA：Athena Scientific Belmont，1995.

[6]王为人，屠梅曾.基于层次分析法的流域水资源配置权重测算[J].同济大学学报：自然科学版，2005，33（8）：1 133-1 138.

[7]王新民，赵 彬，张钦礼.基于层次分析和模糊数学的采矿方法选择[J].中南大学学报：自然科学版，2008，39（5）：875-880.

[8]趙慧娟，汤兵勇，张 云.基于动态规划法的物流配送路径的随机选择[J].计算机应用与软件，2013，30（4）：110-111.

[9]施寒潇.基于AHP算法教师教学质量评估模型的研究 [J].浙江工商大学学报，2006（3）：

51-55.

[10]Saaty T L.What is the analytic hierarchy process[M].Springer，1988.

[11]徐 芹.资源分配问题的动态规划及其 Lingo求解[J].伊犁师范学院学报：自然科学版，2014，8（1）：26-35.

（责任编辑：严 焱）