优化的三电平逆变器无权重因子模型预测控制

赖 华

(宜宾职业技术学院，宜宾 644003)

0 引 言

近年来，二极管钳位型三电平逆变器在中压驱动、可再生能源并网及电动汽车等领域得到广泛关注和应用[1]，其控制方法主要可分为矢量控制和直接功率控制等，控制目标主要包括输出电流或输出功率控制、共模电压抑制、直流侧中点电压平衡控制及开关频率控制等。常规的三电平逆变器控制方法较难实现多目标优化控制，而近年来得到广泛关注的模型预测控制策略在三电平逆变器的控制之中得到深入研究[2-7]。

模型预测控制主要分为连续集模型预测控制和有限集模型预测控制。与连续集模型预测控制不同，有限集模型预测控制采用逆变器的有限个电压矢量和其离散模型进行优化计算，并通过建立目标函数来选择最优电压矢量，并作用于逆变器。该方法由于具有不需要PWM调制单元，实现简单并可同时处理多个控制目标等优点而在电力电子领域得到广泛关注[8-14]。

与两电平逆变器不同，三电平逆变器具有27个电压矢量，且具有多个控制目标，如电流控制、直流侧中点电压平衡控制等，因此其模型预测控制策略较复杂。常规的三电平逆变器模型预测控制策略需要遍历27个电压矢量，因此其计算量较大[8-10]。同时，为了同时实现输出电流控制、中点电压平衡控制和低开关频率控制等多个控制目标，常规的模型预测控制还需要合理的设计权重因子，而目前尚没有成熟的权重因子设计理论[15-18]。

为了克服现有三电平逆变器模型预测控制存在计算复杂、需要设计权重因子的缺点，本文基于分层控制[19]的思想，设计了一种优化的三电平逆变器无权重因子模型预测控制方法。该方法以交流电流和直流侧中点电压平衡为控制目标，优先选择满足交流电流控制的电压矢量，然后再对直流侧中点电压平衡进行优化，从而避免使用权重因子，并实现多目标优化。同时，为了避免每个周期都使用27个电压矢量进行优化，提高逆变器运行的安全可靠性，本文还从3个方面详细研究了三电平逆变器的电压矢量优化选择方法。仿真和实验结果验证了本文所设计的控制策略的有效性。

1 三电平逆变器的数学模型

1.1 连续数学模型

图1给出了二极管钳位型三电平逆变器的电路拓扑。该逆变器每个桥臂包含4个IGBT，其中性点通过二极管连接到直流侧中性点。

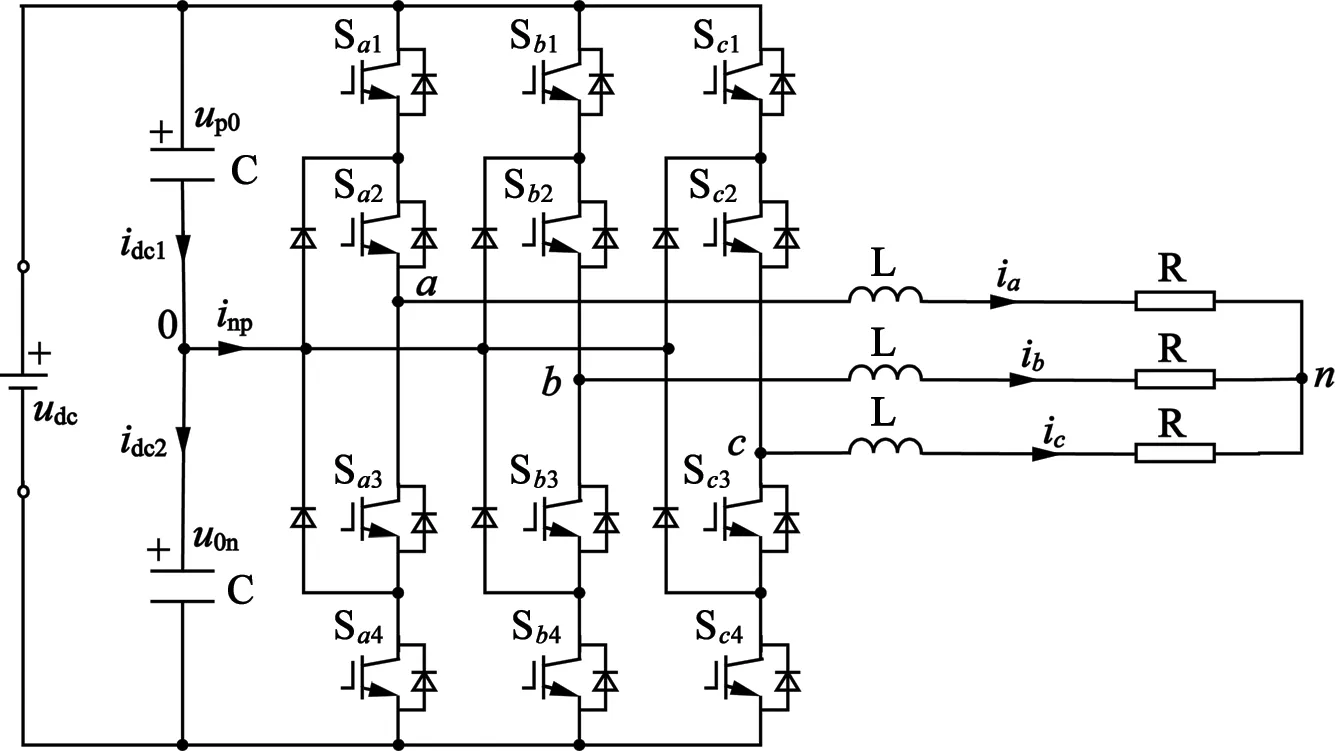
图1 二极管钳位型三电平逆变器的电路拓扑

设Si(i=a,b,c)为三电平逆变器的开关函数，以a相为例，其定义满足：

(1)

根据式(1)的定义，可得三电平逆变器的所有27个电压矢量，其矢量分布如图2所示。

图2 三电平逆变器的电压矢量

与两电平逆变器的8个电压矢量相比，三电平逆变器具有更多的电压矢量，因此其输出电压电流的谐波更小，但同时其控制目标也较多。

由图1和基尔霍夫电压定律可得：

(2)

式中：i=[ia,ib,ic]T为三相相电流；v=[van,vbn,vcn]T为三相相电压。

三电平逆变器输出的电压矢量和开关函数之间的关系可表示：

(3)

设u0=up0-u0n为三电平逆变器的直流侧中点电压[6]，则其满足：

(1-|Sc|)ifc]

(4)

1.2 离散数学模型

为了进行预测控制，需要对上述三电平逆变器的连续数学模型进行离散化，在一个控制周期Ts内，变量x的微分可近似表示：

(5)

根据式(5)可得电流的离散数学模型：

(6)

根据式(5)可得直流侧中点电压的离散数学模型：

(7)

在实际的预测过程中，控制器根据当前时刻的电压矢量和式(3)得出电压矢量值，然后根据式(6)和式(7)分别进行电流和直流侧中点电压的预测，并最终选择出最优矢量。

2 优化的无权重因子模型预测控制方法

2.1 权重因子消除方法

为了同时实现三电平逆变器电流和直流侧中点电压平衡控制，常规的模型预测控制方法需要在目标函数中设计权重因子，其典型的目标函数可表示：

g=|i*-i|+λdc|up0-u0n|

(8)

式中：λdc为权重因子。

本文采用分层控制的思想分别对电流和直流侧中点电压平衡进行控制[19]。

首先，本文定义电流控制目标函数：

g1=|i*-i|≤δi

(9)

式中：δi为电流控制环宽。

式(9)表明，可以将电流控制在环宽δi之内的电压矢量可以用于对直流侧中点电压进行优化控制。而直流侧中点电压平衡的控制目标：

g2=|up0-u0n|

(10)

根据式(10)，对满足电流控制要求的电压矢量进行直流侧中点电压平衡优化，使g2最小的电压矢量为最终的最优矢量。

2.2 电压矢量优化选择方法

常规的三电平模型预测控制方法常常采用27个电压矢量进行优化运算，其计算量较大，且存在逆变器安全运行风险较大的缺点。本文对此进行了详细分析。

首先，从只允许相邻矢量切换的角度考虑，大矢量、中矢量、小矢量和零矢量所对应的备选矢量集如下所述。

以k时刻作用的矢量为大矢量u16为例，则k+1时刻的备选矢量为u4,u5,u16,u17,u27；

以k时刻作用的矢量为中矢量u17为例，则k+1时刻的备选矢量为u4,u5,u6,u7,u16,u17,u18；

以k时刻作用的矢量为小矢量u4为例，则k+1时刻的备选矢量为u1,u2,u3,u4,u5,u6,u7,u14,u15,u16,u17,u27。

若k时刻为零矢量，以u1为例，则k+1时刻的备选矢量为u1,u2,u3,u4,u5,u6,u7,u8,u9,u10,u11,u12,u13,u14,u15。

其次，从减小共模电压的角度考虑，结合式(4)可知，3个零矢量产生的共模电压也不相同。其中，零矢量(111)和(-1-1-1)产生的共模电压较大，而u1(000)则不产生共模电压。因此，在选择零矢量时，仅考虑u1(000)。

第三，从减小电压变化率的角度考虑，对三电平逆变器而言，其相电压和线电压可表示如下：

(11)

(12)

由式(11)可知，为了保证相电压变化量不超过Udc/2，则不允许1和-1之间进行切换。

为了保证每个周期内线电压的变化为在Udc/2之内，根据式(12)作如下分析。

首先，通过分析可知，三电平逆变器任意两种开关状态的组合有如下6种，即：(0,-1)，(0,1)，(0,0)，(-1,-1)，(1,1)，(1,-1)。这6种开关状态组合的差的绝对值分别为：1，1,0,0,0,2。由此可见，为了限制每个周期内线电压的变化，需要禁止开关状态组合{(1,0)—(1,-1)},{(-1,-1)—(1,-1)},{0,0—1,-1},{-1,-1—1,-1}之间切换。

上述电压矢量选择方案减小了du/dt，降低了EMI噪声，提高了逆变器运行的安全性。

综上，本文所设计的电压备选矢量选择方案可总结如下：

(1)只选择上一周期作用的电压矢量及其相邻电压矢量作为备选矢量；

(2)选择零矢量时，只选择(0,0,0)；

(3)禁止开关状态1和开关状态-1之间直接进行切换；

(4)不允许Sa，Sb，Sc中的任意两相由{0,0—1,-1}—1-1切换。

为了清晰起见，图3给出了本文设计的模型预测控制算法框图。

图3 模型预测控制算法框图

3 仿真研究

为了验证算法的有效性，进行了仿真验证，仿真中所使用的参数如表1所示。

表1 仿真参数

首先，图4给出了电流设为15A，电流环宽设定为4A时的稳态仿真结果。由图4(a)可见，电流被控制在设定的环宽之内，这验证了本文所设计的预测电流控制策略的有效性。同时，由图4(b)可见，直接侧中点电压也实现了平衡控制。中点电压偏差在±1V之内，如图4(c)所示。这表明，本文设计的无权重因子控制策略可以很好地实现电流和中点电压平衡等多个目标的控制，验证了所设计的控制策略的有效性。

(a) 指令电流、实际电流、电流误差

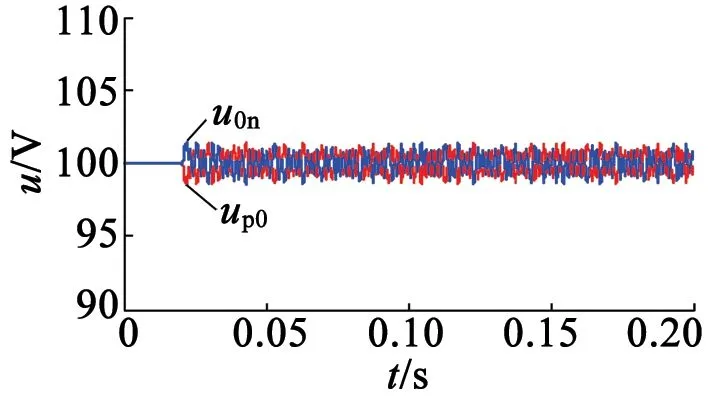
(b) 中点电压

(c) 中点电压偏移量

其次，图5给出了直流侧中点电压存在偏差时的动态仿真结果，以进一步验证本文的控制策略的有效性。此时，电流依然设为15A，电流环宽依然设定为4A。仿真时，设定直流侧初始电压偏差为±50V。

图 5(a)给出了a相电流的仿真结果。由于在0.02～0.03s之间，直流侧中点电压偏差较大，导致电流也出现了一定的畸变。但是，在本文的控制策略的作用下，直流侧中点电压偏差迅速减小，如图5(b)和图5(c)所示。0.05s之后，系统的电流和中点电压均实现了稳定控制，如图5所示。这进一步验证了本文所设计的控制策略的有效性。

(a) 指令电流、实际电流、电流误差

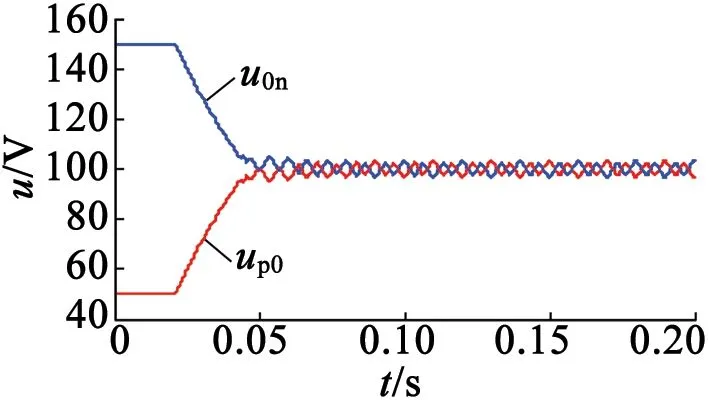
(b) 中点电压

(c) 中点电压偏移量

4 实验研究

为了对所设计的控制策略进行验证，搭建了三电平逆变器的实验平台，如图6所示。主控芯片选择为DSP28335。实验平台主要包括控制板、逆变器主电路、信号采集板和负载等几部分。实验中的参数与仿真一致，如表1所示。

图6 实验平台

图7给出了电流幅值为15A、电流环宽为4A时采用本文的控制策略所得到的稳态实验结果。其中，Sa1为驱动信号，Uab为线电压。由图7可见，本文的方法可以同时实现电流控制和直流侧中点电压平衡控制，且无需权重因子。

图8给出了直流侧电压存在偏差时的采用本文的控制策略所得到的动态实验结果。实验时，电流环宽依然设定为4A。

图7 稳态实验结果

图8 动态实验结果

由图8可见，当电流指令设定为15A时，由于调制度较大，小矢量的使用较少，因此其直流侧上下电容电压可以自动平衡。当电流指令突减为10A时，调制度减小，此时小矢量的使用增多，无中点电压平衡控制时，其直流侧电压偏差迅速增大，电流也出现了明显的畸变，如图8(a)中的区域A所示。当加入中点电压平衡控制后，直流侧电压迅速恢复平衡，如图8(a)中的区域B所示。图8(b)对图8(a)中的区域B进行了放大。由图8(b)可以清楚地看到，加入本文的中点电压平衡控制策略时，直流侧电压迅速恢复平衡，电流的畸变率也明显减小。由此可见，本文所设计的优化无权重因子模型预测控制方法可以同时实现电流和直流侧电压平衡控制，且具有较好的动稳态特性。

5 结 语

本文提出了一种优化的三电平逆变器无权重因子模型预测控制方法。该方法分别对电流和直流侧中点电压平衡进行控制，从而消除了权重因子。同时，该方法给出了最优的电压矢量选择方法，从而简化了算法，提高了逆变器的安全运行性能。仿真和实验结果验证了该方法的有效性。

[1]ALEPUZS,BUSQUETS-MONGES,BORDONAUJ,etal.Interfacingrenewableenergysourcestotheutilitygridusingathree-levelinverter[J].IEEETransactionsonIndustrialElectronics,2006,53(5):1504-1511.

[2]MARTINEZJCR,KENNELRM,GEYERT.Modelpredictivedirectcurrentcontrol[C]//IEEEInternationalConferenceonIndustrialTechnology.IEEE,2010:1808-1813.

[3] GEYER T,OIKONOMOU N,PAPAFOTIOU G,et al.Model predictive pulse pattern control[C]//Energy Conversion Congress and Exposition.IEEE,2011:3306-3313.

[4] 刘涛涛,黄落成,张晓.三电平有源电力滤波器模型预测电流控制方法研究[J].工矿自动化,2013,39(9):100-103.

[5] 杨勇,樊明迪,谢门喜,等.三电平三相逆变器快速有限控制集模型预测控制方法[J].电机与控制学报,2016,20(8):83-91.

[6] 王付胜, 文鹏, 张兴.三电平环宽自适应准定频滞环模型预测控制研究[J].电气工程学报,2016,11(4):9-14.

[7] 夏长亮,张天一,周湛清,等.结合开关表的三电平逆变器永磁同步电机模型预测转矩控制[J].电工技术学报,2016,31(20):83-92.

[8] VARGAS R,CORTÉS P,AMMANN U,et al.Predictive control of a three-phase neutral-point-clamped inverter[J].IEEE Transactions on Industrial Electronics,2007,54(5):2697-2705.

[9] RODRIGUEZ J,PONTT J,CORTES P,et al.Predictive control of a three-phase neutral point clamped inverter[C]//Power Electronics Specialists Conference,2005.IEEE,2005:1364-1369.

[10] RODRIGUEZ J,CORTES P.Predictive control of a three-phase neutral-point clamped inverter[M]//Predictive Control of Power Converters and Electrical Drives.John Wiley & Sons,Ltd,2012:65-79.

[11] 张永昌,杨海涛.异步电机无速度传感器模型预测控制[J].中国电机工程学报,2014,34(15):2422-2429.

[12] 刘普,王跃,丛武龙,等.模块化多电平换流器优化模型预测控制策略研究[J].中国电机工程学报,2014,34(36):6380-6388.

[13] 杜少通,伍小杰,周娟,等.一种采用虚拟磁链模型预测的新型PWM算法[J].中国电机工程学报,2015,35(3):688-694.

[14] 罗德荣,姬小豪,黄晟,等.电压型PWM整流器模型预测直接功率控制[J].电网技术,2014,38(11):3109-3114.

[15] 张永昌,杨海涛.感应电机模型预测磁链控制[J].中国电机工程学报,2015,35(3):719-726.

[16] ROJAS C A,RODRIGUEZ J,VILLARROEL F,et al.Predictive torque and flux control without weighting factors[J].IEEE Transactions on Industrial Electronics,2013,60(2):681-690.

[18] LIM C S,LEVI E,JONES M,et al.FCS-MPC-Based current control of a five-phase induction motor and its comparison with pi-pwm control[J].IEEE Transactions on Industrial Electronics,2013,61(1):149-163.

[19] CARRARO M,ZIGLIOTTO M.Hierarchical direct predictive control of PMSM drives[C]//Predictive Control of Electrical Drives and Power Electronics.IEEE,2011:3-9.