数学教学中《圆》探究性问题的设计及反思
2017-05-28王柱华
王柱华
摘要:《义务教育数学课程标准(2011版)》中明确指出:在参与观察、实验、猜想、证明、综合实践等数学活动中,发展合情推理和演绎推理能力,清晰地表达自己的想法。建立数感、符号意识和空间观念,初步形成几何直观和运算能力,发展形象思维与抽象思维。
關键词:《圆》 探究性问题 设计及反思
圆中的四角关系 :通过运动变化、从而引出定义,培养学生的观察运动变化的能力和数学建模思想。
圆周角与圆心角都是由各自顶点在圆中所处的位置决定得。由于事物之间都存在因果关系,它们的本质特征最容易从运动中显示出来。如何把静止的问题变成动态的问题?本节课让学生感受到图形运动的真谛。
一、相关的知识链
1.圆周角定理:
圆周角等于它所对弧上的圆心角的一半。
2.圆周角定理的推论4:
圆内接四边形对角互补。
3.切线的性质定理:
圆的切线垂直于经过切点的半径。
4.切线长定理:
过圆外一点所画的两条切线长相等。
5.同弧(等弧)所对的圆周角相等。
二、圆中的四角关系在中考中的地位
在近几年各地的中考中,圆的有关性质, 仍是中考命题的热点.考查了学生综合运用知识以及转化思想来解决问题的能力,圆的对称性和切线是圆中的重点,求角度和线段长是考试常考的题型。
三、四角关系详解
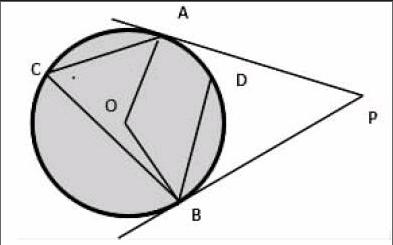
1. ∵AP、BP是⊙o的切线
∴OA⊥AP、OB⊥BP
∴∠PAO=∠PBO=90度
∴∠AOB+∠P=180度
2.∠AOB和∠ACB是劣弧所对的圆心角和圆周角
故,∠AOB=2∠ACB
3. ∵四边形ACBD内接于⊙o
∴∠C+∠D=180度
当一个角的顶点运动到圆内时,这个角我们叫它圆内角;当这个角的顶点运动到圆外时,这角叫做圆外角;当这个角的顶点运动到圆心时,已知它是圆心角,当这个角的顶点运动到圆上时,这是一种什么角?我们给这样的角起个什么名字呢?
我们通过这个角运动变化的演示,得到了圆周角的由来,从而归纳概括出圆周角的有关定义,引出圆周角的课题。前面是引入圆周角定义的过程,它不仅使学生了解到概念产生的过程及概念本质的特征,还加深了对隐含概念本身的动静辩证思想的理解和认知过程。
试题在线
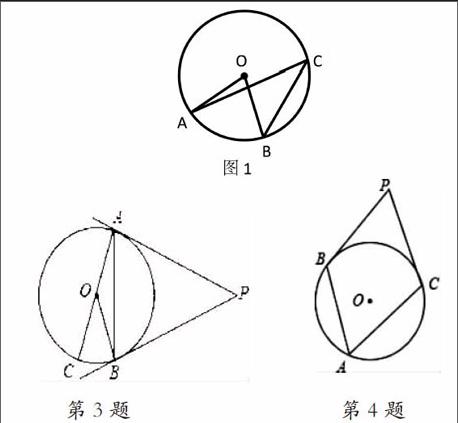
1.如图1在⊙O 中,∠ACB=20度,则∠AOB= ___度.
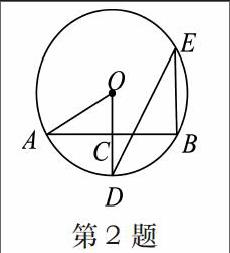
2.如图AB是⊙O的弦OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.若∠BED=30°,⊙O的半径为4,则弦AB的长是( )
3.(菏泽)如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,则∠BAC= 度.
4.(2014·连云港)如图,圆周角∠BAC=55°,分别过B,C两点作⊙O的切线,两切线相交与点P,则∠BPC= _______°
1.分析:此考查了圆周角定理:在同圆或着等圆中,同弧或等弧所对的圆周角相等,他们都等于这条弧所对的圆心角的一半。
2分析:此题涉及圆中求半径的常见问题,此类题在圆中涉及到弦长、半径、圆心角的有关计算问题,我们常把半弦长与半径与圆心到弦距离这三者变形到同一直角三角形中,之后再通过勾股定理进行计算。
3.分析:该题考点是常考点,关于圆的性质比较多,学生要熟记并避免混淆。
4.分析:故答案为:70。
总之,在教学中,始终以学生作为课堂主体,鼓励学生多动手、多动口、多动脑,尽量在教学中预设一些图形转化的问题来激发学生的求知欲,满足学生像多元化的发展新时代的需求。
圆中的四角恋,学生解决这一问题是有相当难度的,尽管如此,教学过程中让学生从多种角度直观体验数学建模思想,而这也正是本章学习的主要目标。另外,没有充分考虑到不同层次学生的需求。
(作者单位:山东省聊城市莘县妹冢镇初级中学)
