均匀试验设计及DPS数据处理与分析

曹艳文+潘世强

摘 要：均匀设计法是继华罗庚教授普及、倡导的优选法和国内普及推广的正交法之后应用较为广泛的统计试验分析方法。本文即是采用均匀设计法进行的试验设计。同时利用DPS 数据处理软件进行数据处理和分析，该软件可以为试验提供多类多元分析，如多元方差分析、回归分析、有偏回归分析、多因素分析等，还可以对数据进行统计，建立数学模型。

关键词：均匀设计；DPS数据处理系统；回归分析

中图分类号：S-3 文献标识码：A DOI：10.11974/nyyjs.20170532009

目前，国内的均匀设计方法已日趋成熟，并且有一套结构完整的试验表 Un（qs），按照试验表安排所需试验，其中U 代表均匀设计代号，n 代表要做的试验次数，q 代表每个因素的水平，s 代表数据表中列的数目。虽然均匀设计没有正交设计的整齐性，但其灵活性较好，更重要的是，均匀试验可以大大降低试验次数，从实践的角度看可以大大降低成本。由此可以看出其优越性。本文通过实例简述DPS数据处理系统。

1 试验设计

本次试验选取的4个因素分别是螺旋升角、螺距、螺旋外径（螺纹高度）和马达转速，每个因素分别选择6个水平，因素水平表如下表1所示。

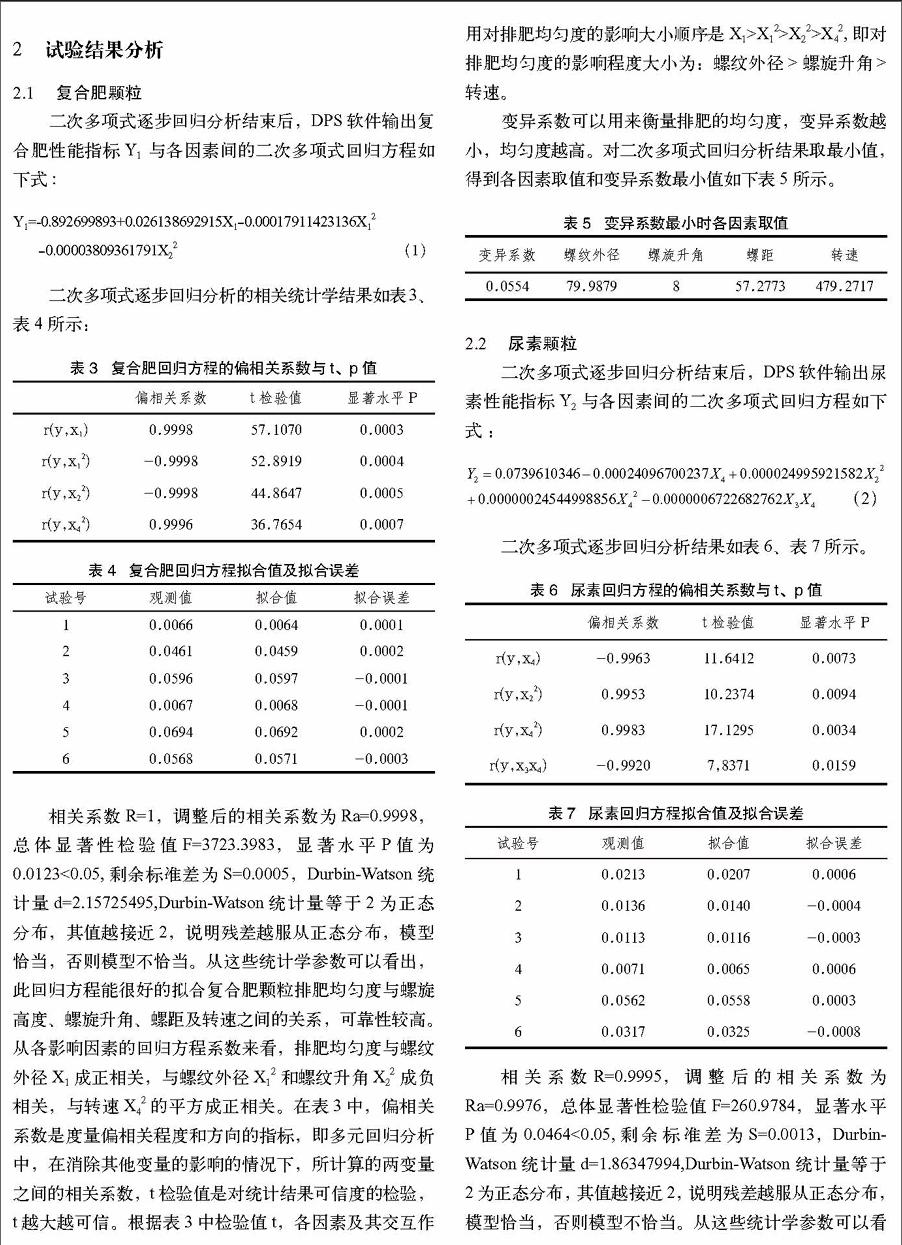
本次试验选用U6（64） 的均匀设计表，进行一次重复组合排列，本次试验的试验方案如下表2，将所需的数据带入试验方案中即每一组的试验条件，X1～X4分别代表螺纹外径、螺旋升角、螺距和螺旋轴转速。

2 试验结果分析

2.1 复合肥颗粒

二次多项式逐步回歸分析结束后，DPS软件输出复合肥性能指标Y1 与各因素间的二次多项式回归方程如下式：

Y1=-0.892699893+0.026138692915X1-0.00017911423136X12

-0.00003809361791X22 （1）

二次多项式逐步回归分析的相关统计学结果如表3、表4所示：

相关系数R=1，调整后的相关系数为Ra=0.9998，总体显著性检验值F=3723.3983，显著水平P值为0.0123<0.05，剩余标准差为S=0.0005，Durbin-Watson统计量d=2.15725495，Durbin-Watson统计量等于2为正态分布，其值越接近2，说明残差越服从正态分布，模型恰当，否则模型不恰当。从这些统计学参数可以看出，此回归方程能很好的拟合复合肥颗粒排肥均匀度与螺旋高度、螺旋升角、螺距及转速之间的关系，可靠性较高。从各影响因素的回归方程系数来看，排肥均匀度与螺纹外径X1成正相关，与螺纹外径X12和螺纹升角X22成负相关，与转速X42的平方成正相关。在表3中，偏相关系数是度量偏相关程度和方向的指标，即多元回归分析中，在消除其他变量的影响的情况下，所计算的两变量之间的相关系数，t检验值是对统计结果可信度的检验，t越大越可信。根据表3中检验值t，各因素及其交互作用对排肥均匀度的影响大小顺序是X1>X12>X22>X42，即对排肥均匀度的影响程度大小为：螺纹外径>螺旋升角>转速。

变异系数可以用来衡量排肥的均匀度，变异系数越小，均匀度越高。对二次多项式回归分析结果取最小值，得到各因素取值和变异系数最小值如下表5所示。

2.2 尿素颗粒

二次多项式逐步回归分析结束后，DPS软件输出尿素性能指标Y2与各因素间的二次多项式回归方程如下式 ：

（2）

二次多项式逐步回归分析结果如表6、表7所示。

相关系数R=0.9995，调整后的相关系数为Ra=0.9976，总体显著性检验值F=260.9784，显著水平P值为0.0464<0.05，剩余标准差为S=0.0013，Durbin-Watson统计量d=1.86347994，Durbin-Watson统计量等于2为正态分布，其值越接近2，说明残差越服从正态分布，模型恰当，否则模型不恰当。从这些统计学参数可以看出，此回归方程能很好的拟合复合肥颗粒排肥均匀度与螺旋高度、螺旋升角、螺距及转速之间的关系，可靠性较高。从各影响因素的回归方程系数来看，排肥均匀度与螺距X3和转速X4成负相关，与螺纹升角X22成正相关，与转速X42的平方成正相关。在表6中，偏相关系数是度量偏相关程度和方向的指标，即多元回归分析中，在消除其他变量的影响的情况下，所计算的两变量之间的相关系数，t检验值是对统计结果可信度的检验，t越大越可信。根据表6中检验值t，各因素及其交互作用对排肥均匀度的影响大小顺序是X42>X4>X22>X3×X4，即对排肥均匀度的影响程度大小为：转速>螺旋升角>螺距。

变异系数可以用来衡量排肥的均匀度，变异系数越小，均匀度越高。对二次多项式回归分析结果取最小值，得到各因素取值和变异系数最小值如下表8所示。

3 小结

本例中，由于本试验的因素水平数较多，因此采用了均匀设计的方法，以减少试验次数，并利用DPS软件进行了试验方案的设计。依据实验方案在实验室进行试验并记录试验结果，然后整理数据并应用DPS数据处理软件对试验数据进行二次多项式逐步回归分析，获得回归方程以及当试验指标最小时各因素的数值大小。

参考文献

[1] 林锦贤. 用均匀设计优化分散聚合法制备P（St/nBA）微球体.计算机与应用化学，2011，28（6）：721-724.

[2]徐伟.季索菲.DPS数据处理系统在生物统计分析中的应用[J].榆林学院学报，2014（24）：24-27.

[3]孙其诚，王光谦.颗粒物质力学导论[M].北京：科学出版社，2009.

[4]杨虎，刘琼荪，钟波，等.数理统计高等教育出版社，2004.

[5]李秀昌.利用DPS数据处理系统进行均匀试验设计与分析[D].长春中医药大学，2010.