部分联网环境下交叉口排队长度估算与信号自适应控制*

林培群 雷永巍 姚凯斌 顾玉牧

(1. 华南理工大学 土木与交通学院， 广东 广州 510640； 2.苏州设计研究院股份有限公司， 江苏 苏州 215021)

浮动车技术是国际智能交通系统中采用的获取道路交通信息的先进技术手段之一.国内各大城市的浮动车建设主要依靠出租车、公交车等营运车辆.近年来，随着移动互联网技术的进步，无论是高德、凯立德等交通信息运营商，还是滴滴、Uber等专车平台，都极大地推动了城市浮动车数量的增长，促进了城市车辆联网环境的建设.随着联网车辆的增加，目前我国城市交通出行环境中联网(如通过移动互联网)的车辆不断增多，一段时间内，联网车辆与非联网车辆并存于城市道路，即“部分联网”.然而现阶段对于城市所处的非完全联网环境下如何更加有效、准确地获取实时的交通状态数据，并据此进行科学合理的交通引导和控制的研究较为鲜见.现阶段国内外学者主要通过研究道路车辆排队长度来设计或评估控制方案.传统的排队长度研究主要是采用概率论、排队论、波动论、累计曲线图解等方法进行，这些方法能够在一定范围内描述交通排队现象，并构建相应的排队长度计算模型[1- 4].随着信息技术的发展，Comert等[5]在已知浮动车市场渗透率(MPR)的条件下，利用浮动车数据研究了平均排队长度的分布情况.Hao[6]以及Cheng等[7]利用车辆行驶时间来估测排队长度.Ban等[8]通过计算浮动车在交叉口范围的行程时间，提出排队延误模式的概念，并重构车辆在交叉口前的实时排队曲线.Goodall等[9]利用车联网技术，提出了低市场渗透率下的排队长度估算方法.

总体而言，目前针对车联网环境下排队长度估算的研究较少.排队长度估算是智能信号控制的基础，而且当前车联网技术不断发展，因此有必要研究不同市场渗透率下基于联网车辆的路段实时排队长度估算方法，以优化交叉口控制，同时获取道路交通状况数据，用来分析交通状态以及进行交通管理.自适应控制技术可快速响应动态交通需求，与固定配时控制相比可在一定程度上提高交叉口的利用率，因此得到了国内外学者的广泛关注.郭谨一等[10]研究了基于Synchro系统的交叉口信号控制，提出了控制参数的确定方法，得出了感应信号控制在低饱和交通状况下可有效降低延误、在接近饱和及过饱和状况下则失去作用的结论.邵锦锦等[11]提出了变相序的多相位感应控制算法，该算法平均延误明显低于传统感应控制.王正武等[12]结合基于规则与基于优化的自适应控制设计了一种自适应公交优先控制方法.然而，现阶段研究主要集中于对交叉口当前相位绿灯进行微调，缺乏整体统筹，局限了优化空间.

文中提出了一个全新的车联网环境下的交叉口控制方案：在进行车辆排队长度估算的基础上，综合考虑交叉口通行安全、相位通行优先级差异性等因素，实现基于交通流向动态组合的交叉口自适应控制设计，以期改善城市道路交叉口的交通拥堵状况，克服传统交叉口感应控制的弊端.

1 方法概述

车联网技术在不断发展，但是联网车辆无法在短期内覆盖到所有车辆，因此，如何在一定车联网市场渗透率下评估路网的交通状况，具有极为重要的实际意义.其中，路段排队长度是判别交通状况的一个重要指标.然而，当联网车辆只占所有车辆的一定比例时，仅将一辆或两辆联网车辆的交通信息作为分析数据效果往往不佳，为此，文中通过研究路段车队的运行轨迹，以此获得突破.

模型运行框架如图1所示.

排队形成后路段所有车辆在不同时刻的“位置-速度”曲线如图2所示.其中，Tn(n=1，2，…,6)为红灯时间内相等间隔的时间序列.

基于以上路段车队在不同时刻的“位置-速度”轨迹曲线，同时考虑到城市中路网密度与道路流量较大且大量道路被交差口分割，造成了每段道路长度较短，车辆在每段道路上的离散程度不高，具有较为明显的车辆跟驰效应的情况，文中将同一车道上的车辆近似视为一个整体，通过分析函数关系来获得较为准确的排队长度，路段上车辆的“位置-速度”轨迹近似呈函数关系.

在红灯阶段，同一车道的车辆分别处于3个阶段：(近似)匀速阶段、减速阶段、排队阶段(速度小于vmin).坐标原点为路段的起始位置，如图3所示.

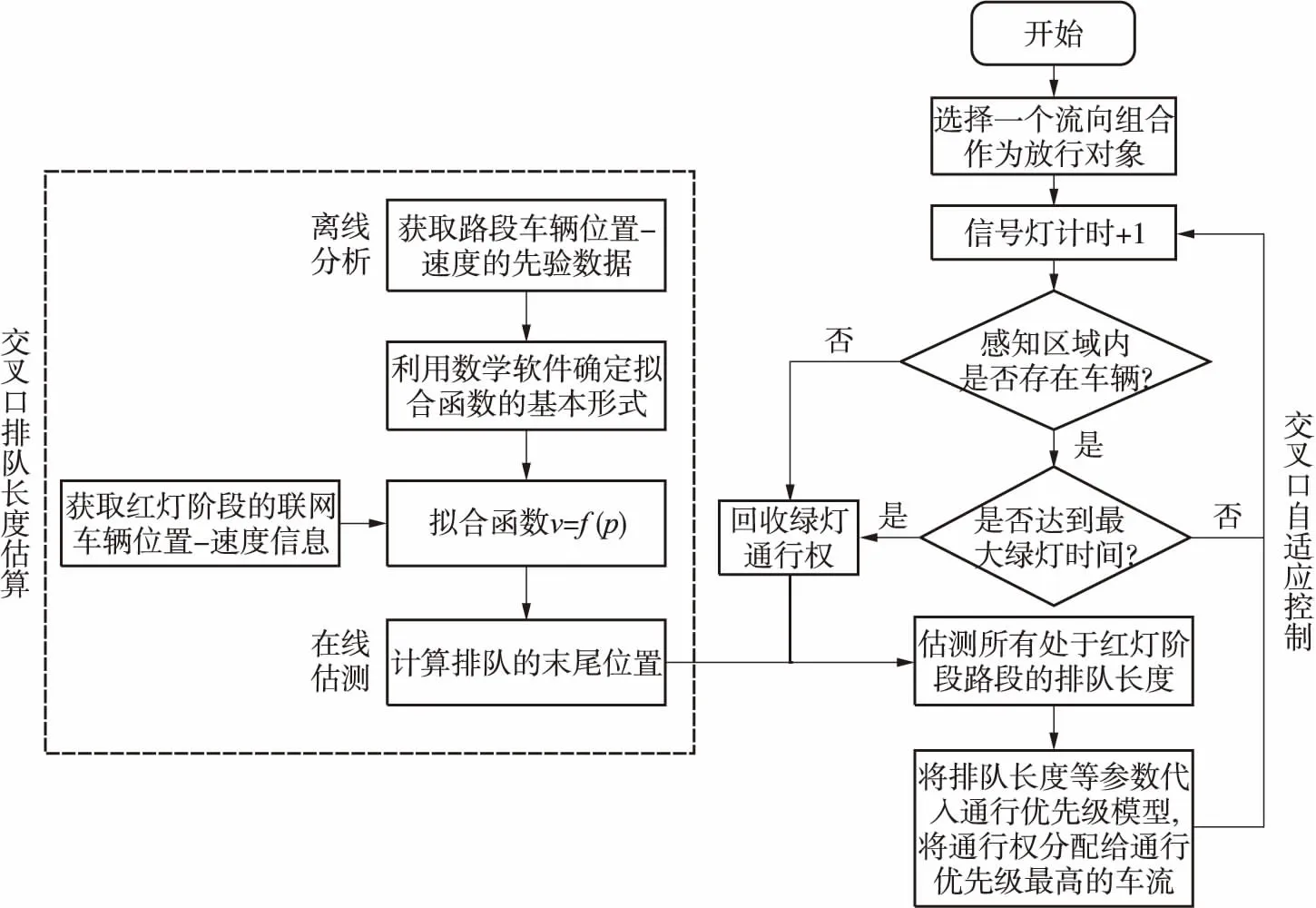
图1 模型运行框架

设车辆位置-速度关系的拟合函数形式为

v=f(p)

(1)

式中，v表示速度，p表示位置.

根据获取的联网车辆位置-速度信息，以选取的拟合函数形式(式(1))为参考，求解函数的各个参数，近似获得整个路段车队的轨迹.求得坐标P(p′，vmin)，即获得了排队车辆的末尾位置.路段的长度为L，则排队长度为L-p′.

由于多项式函数可能会求解出p′的多个解，最终的值可以按照以下原则选取：①p′必须是实数； ②p′必须在0～L之间；③p′最接近于上一次求解所得的数值.

2 排队长度估算

根据前述算法思路，提出以下估计排队位置的方法，具体估测过程如下：

(1)初始化(离线) 观察较长时间内的路段情况，获得路段所有车辆的自由行驶速度(v0)以及车队位置-速度信息，以此确定拟合函数的基本形式(如二次函数、三次函数等).

(2)数据获取(在线) 在红灯阶段，可以实时获得当前所有联网车辆的位置-速度数据.

(3)函数拟合 选取当前路段内联网车辆中处于减速阶段的车辆(速度介于vmin和v0-b之间，其中b根据实际路段情况确定，文中取为3)；使用其位置-速度信息，以离线阶段拟合函数基本形式为依据，拟合当前数据下的“位置-速度”曲线函数.

(4)计算 由拟合函数求出P点位置，进而求出排队长度.红灯阶段的每个时刻都可用以上的方法估测排队长度.倘若处于减速阶段的联网车辆少于3辆(难以准确拟合函数)，或按照p′求解原则依旧无解，则近似取上次的排队位置加上路段一个平均排队车头间距(即假设在检测时间内又有一辆车停下).

3 基于流向动态组合的交叉口自适应控制模型

传统的交通检测方法在检测排队长度方面存在一定的难度和缺陷.例如，若使用线圈，则需要连续铺设多个线圈，不经济实用；若使用视频检测，会遇到外物遮蔽以及夜间可视度低等问题.引进新型的车联网技术可以有效地弥补这些缺陷，在误差允许的范围内，实时估测排队长度，同时将车联网技术应用到浮动车上，即将浮动车获取的数据实时上传至后台数据中心，通过数据分析获得交通量等数据，再结合排队长度估测算法，提出车联网环境下的新型交叉口自适应控制.

3.1 控制思想

在传统控制中，一个相位通常绑定多股车流，这些车流拥有相同的控制节奏和通行时间，因此会浪费部分通行效率.车联网环境下，文中赋予交叉口车辆各基本流向完全独立的控制逻辑，改变了传统上由若干股车流绑定在一起、拥有相同控制节奏和通行时间的做法，由此进行无冲突流向的动态交叉口信号控制组合，以便更高效地利用交叉口的通行时隙.

同时，文中以头车等待时间、排队长度、交通流量作为优化模型的基本输入参数.得益于无线传感、图像识别等车联网技术的快速发展和日趋成熟，以上基础参数的获得不再是技术难点.另外，在获取实时交通数据的基础上，文中还建立了量化各流向通行优先级的数学模型，在保障安全的前提下，及时回收低通行效率车流的通行权，将其分配给高通行优先级的车流，从而达到提高道路时空资源利用率的目的.

3.2 流向组合

对于每一个交叉口而言，在确定了各进口道的车道功能之后，即可准确判断任意两股车流是否存在冲突.文中用A={1，2，3，…，n}表示进口道的编号集合，用H={Le，Ri，St}表示车道的转向集合，其中n表示进口道的数量，Le表示左转，Ri表示右转，St表示直行.

进口道和转向的组合(a，h)(a∈A，h∈H)表示一个流向(一个进口的某个方向，可能包括多个车道)，记为f.以交叉口所有可能出现的流向为元素的集合称为流向总体，记为T.由T的定义可得T⊆A×H，A×H表示集合A和H的笛卡尔积.由于A和H是有限集，可推导出T也是有限集，且|T|≤|A|·|H|.

若F={f1，f2，…，fm}(f1，f2，…，fm∈T，m≤|T|)满足∀i≠j(i，j≤m)，fi与fj不发生冲突，则称F为一个流向组合.以所有流向组合为元素的集合称为流向组合集，符号记为C(T).由F的定义可得C(T)⊂Q(T)，Q(T)表示T的幂集.由此可推导出C(T)是有限集，且|C(T)|<2|T|.

3.3 交通流感知区域设置

文中提出的交通流感知有别于传统的采用定点线圈检测新增车辆到达情况的做法，而是取各进口道停车线前x米的路段范围作为感知区域.x的取值要满足尚未进入感知区域的车辆能够无不适感地减速至停车线前的要求，即

(2)

式中，v表示安全通过交叉口的速度，μ表示无不适感的减速度，一般取-1.5～-2.5 m/s2.

传统感应控制方案中，驾驶员驶近停车线时可能突遇红灯后紧急刹车，此种情况容易造车追尾隐患，同时降低舒适度.文中提出的路段感知方式可以较好地解决这个问题.只要感知区域内存在车辆，绿灯时间将适当延长，直至清空区域内的车辆或者达到最大绿灯时间.实际操作中，可在感知区域的首、末设置感应线圈，通过进、出的车辆数来判断是否有车辆在感知区域中.

3.4 通行优先级

3.4.1 相关概念

有冲突的不同流向交通流本质上是竞争关系，交叉口控制系统的任务就是进行通行资源的统筹分配，为不同流向的交通流安排合理的绿灯时隙.由于交通系统具有较高的复杂性和随机性，如何科学地进行通行资源的统筹分配是学术界尚未解决的问题.李鹏凯等[13]根据车联网环境下的车-车、车-路实时通信特征，以车辆停车等待时间最小为优化目标建立信号控制交叉口面向个体车辆的车速引导模型，并通过试验验证发现所提出的方法能有效降低车辆延误；Fortelle[14]基于完美的车联网技术环境假设，提出车辆自主驾驶通过交叉口的控制思想，即路口收集每辆车的速度、位置等信息，并给每辆车提供一个可在穿越交叉口时避开潜在冲突的解决方案，但并未给出具体的模型和求解方法.

为了对问题进行更精确的数学建模，文中从交通控制的角度选择车辆到达率、排队长度、所在道路的等级作为通行优先级计算模型的输入参数，以此科学、合理地量化优先指标.

3.4.2 基于延误时间最小化的通行优先级计算模型

一段时间内，总延误时间D等于所有车辆的延误时间之和：

(3)

式中，di表示第i辆车的延误时间，n表示研究时间段内的总车辆数.

当控制相位切换时，控制系统通过联网车辆数据估测排队长度.设其中某个等候车队的车辆数为n1，头车的等待时间为tw，平均到达率为q，饱和流量为S，分以下3种情况进行研究：

(1)n1=0 此时不存在排队，D=0.

(2)n1>0，S>q如果该车队分配到绿灯且绿灯时间足够长，则排队车辆将得以清空.演化过程如图4所示.

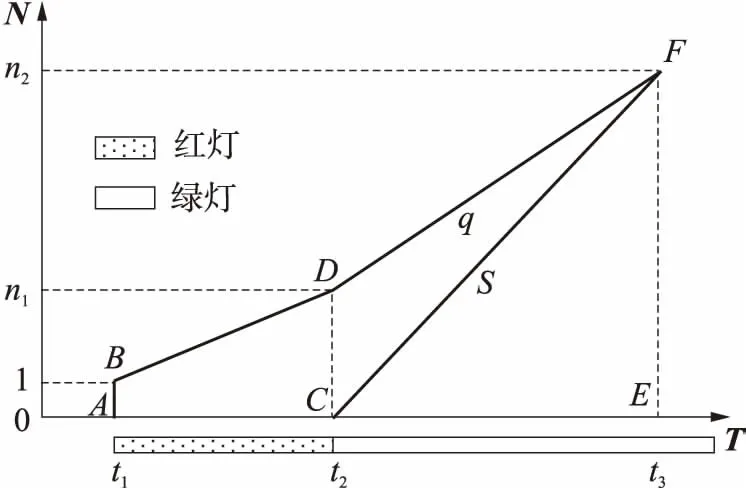
图4 S>q条件下的延误时间分析图

此时总延误时间等于图4中梯形ABDC和三角形DCF的面积之和，即

(4)

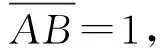
(5)

(3)n1>0，S≤q如果该车队分配到绿灯且假定输入交通量在短时间内保持不变，此时排队车辆数将随时间不断增加，绿灯时间不断延长，直至达到最大绿灯时间tmax.演化过程如图5所示.

此时总延误时间等于图5中梯形ABDC和梯形DCGF的面积之和，即

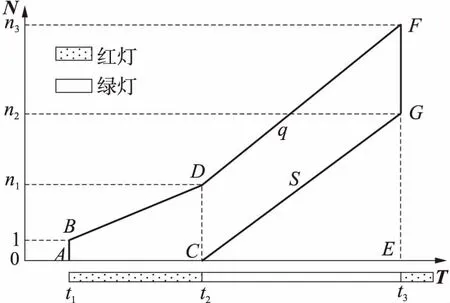
图5 S≤q条件下的延误时间分析图

(6)

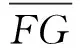
(7)

将已知量代入式(7)，可得

(8)

综上所述，车流f的总延误时间D(f)的计算公式如下：

(9)

在上述排队车辆延误时间计算模型的基础上，可进一步确定交通流向的通行优先级，即

M(f)=kD(f)，k>0

(10)

式中，M(f)为车流f的通行优先级，D(f)为总延误时间，k为加权系数(一般情况下主干道的加权系数较高).

3.5 通行权切换判决算法

通行权切换判决算法的作用在于判断是否终止某股车流的通行.若当前流向组合里某股车流至少满足以下规则中的一条，则终止该车流的通行：

①车道预设的感知区域内不存在车辆；

②车流的绿灯时间超过了预设的最大绿灯时间.

判决算法的作用对象是每一股车流，因而一股车流停止通行并不会影响到其他车流.具体的流程如下所述：

步骤1 通行权切换到某个流向组合，控制系统监控当前流向组合里所有车流所在的感知区域，并为其中的每股车流独立分配一个绿灯时间．

步骤2 判断当前放行的每股车流是否满足通行权切换规则.如果有若干股车流满足终止通行规则，则回收这部分车流的通行权，执行步骤3；否则每股车流的绿灯时间增加1个基本单位(如1 s)，重新执行步骤2.

步骤3 根据3.4.2节中的通行权分配模型进行计算，将步骤2中回收的通行权分配给通行优先级最高的车流；返回执行步骤1.

3.6 通行权分配优化模型

在控制过程中，当有一股或多股车流满足切换规则时，这部分车流的通行权将被回收.记当前处于放行状态的流向组合为Fc，满足切换规则的车流集合为Fr，则保留通行权的车流集合为

Fl=Fc-Fr={(f|f∈Fc，f∉Fr}

(11)

接下来要确定一个不与Fl发生冲突的车流集合Fa并授予其通行权，与Fl动态组合成为下一个放行的流向组合.Fa必须符合以下条件：

(12)

通过遍历流向组合集C(T)，其中真包含Fl的元素与Fl的差集即是式(11)的可行解，所有可行解构成解空间M，表示为

M={(F-Fl|F∈C，F⊃Fl，F≠Fc}

(13)

考虑到存在|M|>1的情况，因此文中通过建立数学规划模型来求解最优的Fa.定义车流集合F的通行优先级为F中所有元素的通行优先级之和，记为P(F).通行优先级越大，表示通行紧迫程度越高，交叉口的利用率越大.因此，拥有最高通行优先级的F即是最优解.用数学描述如下：

(14)

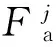
4 算例分析

采用C#语言对VISSIM仿真平台进行二次开发(基于COM接口)，以实现上述排队长度估算和新型自适应控制方案.程序进行了严格的逻辑检查与测试，确保其在应对大型交叉口时仍能稳定运行.算例中选择典型平面交叉口，首先对排队长度估测方案的有效性进行验证，在此基础上对3种不同的交通控制方式(固定配时、传统感应控制以及文中提出的交通流向动态组合式感应控制)分别进行仿真.仿真实验采用控制变量法，分别获取不同交通量输入环境下的平均排队长度、平均延误时间和平均停车次数作为评价指标，以此分析车联网环境下的新型交叉口自适应控制的可行性和适用范围.

选择一个典型的十字型交叉口作为研究对象.交叉口每个进口均包含3条车道，分别是专用左转、直行和右转车道.右转车道采用渠化分流的交通控制策略，不受信号灯控制，因此交叉口共有8股车流相互竞争通行权.仿真界面如图6所示，参数设置见表1.

图6 仿真界面

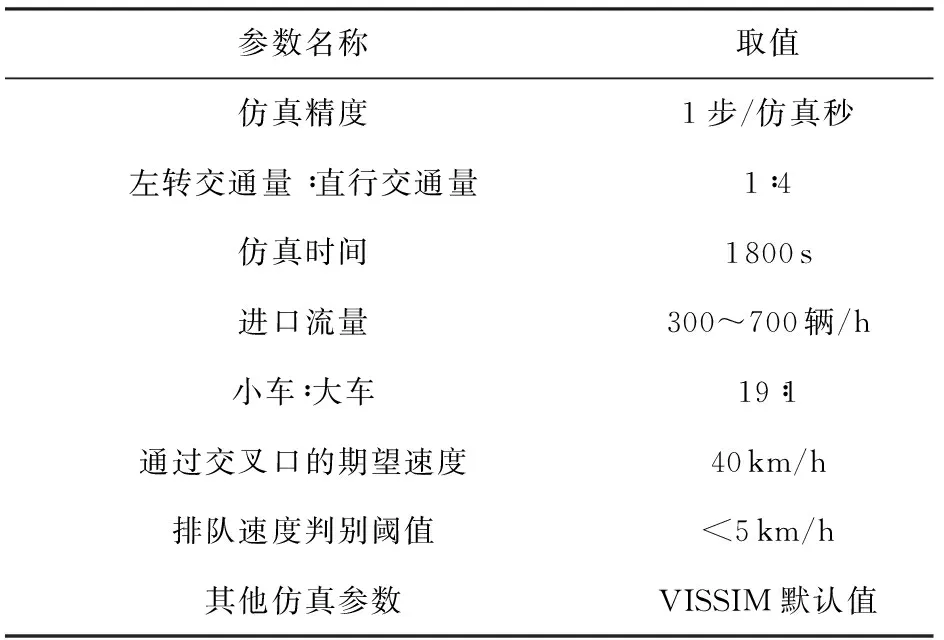
表1 标定参数

4.1 排队长度估算

通过分析交叉口一段时间内的车辆“位置-速度”曲线，确认其拟合函数符合三次函数基本形式.实验结果表明，在MPR大于50%的情况下波动性较小，能够稳定拟合，此时与文献[15]中高市场渗透率的情况相同，效果较为理想，结论也相似.当MPR小于50%时，减速区间的联网车辆数过小，无法稳定拟合，波动性较大，此时可以选用文献[4]中低市场占有率的方案.实验过程中3个不同MPR下的随机红灯时间阶段的实验结果如图7所示.

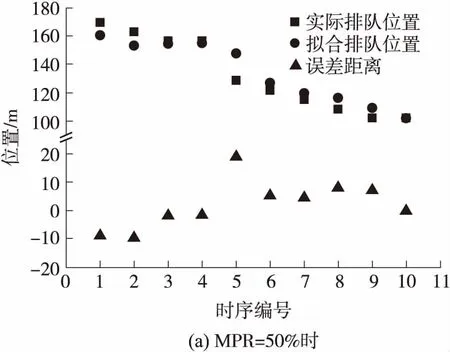
图7 排队长度估算结果

根据Wiedemann模型，排队车队中平均车头间距为7.25 m.实验结果表明，采用文中提出的方法，获取的排队位置误差集中在1到2辆车，极少情况下会有3到4辆车，证明在城市道路中文中方案有一定的实用性和可行性.

4.2 交叉口3种控制方案对比

(1)固定配时

考虑到对向直行和对向左转交通量相当，固定配时方案采用四信号相位循环对称放行.配时方案根据韦伯斯特公式计算得到，其中默认饱和流量为1800辆/(h·车道)，损失时间为3 s，黄灯时间为3 s，不设全红时间.当单进口流量达到900辆/h时，交叉口进入饱和状态.此时，固定配时方案失效，后半段没有仿真数据，不列入比较.

(2)传统感应控制

相位设计与固定配时相同，均为循环对称放行.检测线圈距离停车线36 m，初始绿灯时间为10 s，单位绿灯延长时间为3 s，最大绿灯时间为60 s.

(3)文中方法

经式(1)计算得感知区域的长度为25 m(取v=40 km/h、a=-2.5 m/s2)，基本时钟单位为1 s，最大绿灯时间取经验值60 s.各进口的道路等级相同，k均取值1，联网车比例大于70%.

通过多次仿真实验，获取3种控制方案下的交通运行参数，并对各个参数取平均值，实验结果如图8所示.

从实验结果可以看出，随着单进口交通流量的增加，3种信号控制方案的3项评价指标都在上升，但文中方案的上升趋势相对平缓.与另外两种控制方案相比，文中方案对平均排队长度的优化幅度最明显，达到了70%左右，这主要是因为控制系统及时为高通行优先级的流向安排了通行时隙，快速疏散了排队车辆.此外，与其他两种控制方案相比，平均延误时间分别降低了约65%和55%.在平均停车次数方面，当单进口流量小于800辆/h时，文中方法与传统感应控制方案的效果非常接近.值得注意的是，从近饱和状态(单进口流量大于800辆/h)开始，文中方案较之传统感应控制方案停车次数增多，但最为关键的通行延误和排队长度下降明显.停车次数增多的原因是文中方案总是让交叉口工作在高效率的状态下，因此会损失一小部分车辆的效率，如某些进口的“队尾车辆”往往需要二次停车.

综上，文中所提出的控制方案在高交通负荷的条件下保持了良好的控制效果，科学、合理地弥补了传统感应控制的短板.

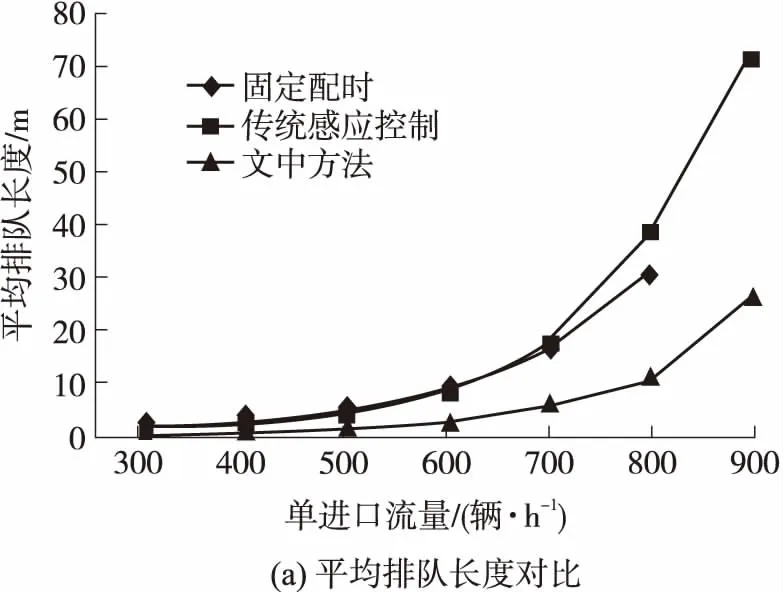
图8 交通系统运行指标对比

5 结语

文中设计了交叉口排队长度估测算法，建立了进口道交通流的通行优先级计算模型，并以此度量各股车流通行的优先级，在此基础上实现了车联网环境下交通流向动态组合的自适应控制.通过对VISSIM平台二次开发后进行了仿真实验，结果表明所获取的排队位置误差集中在1到2辆车.相比于传统感应控制和固定配时设计，文中提出的基于交通流向动态组合的交叉口自适应控制方法在交叉口平均排队长度的优化幅度方面达到了70%左右，平均延误时间分别降低了约65%和55%，弥补了传统感应控制在接近饱和及过饱和交通状态下疏导能力不足的缺陷，切实有效地提高了部分联网环境下交叉口的运行效率.下一阶段将选取更多的交通环境对模型进行测试和验证.

：

[1] VIGOSA G，PAPAGEORGIOUA M，WANG Y.Real-time estimation of vehicle-count within signalized links [J].Transportation Research Part C:Emerging Technologies，2008，16(1):18- 35．

[2] 祁宏生，王殿海.信号控制交叉路口车辆排队长度 [J].吉林大学学报(工学版)，2009，39(6):1457- 1462．

QI Hong-sheng，WANG Dian-hai.Vehicle queue length at signal controlled intersection [J].Journal of Jilin University(Engineering and Technology Edition)，2009，39(6):1457- 1462．

[3] DAGANZO C F.Queue spillovers in transportation networks with a route choice [J].Transportation Science，1998，32(1):3- 11．

[4] 王殿海，景春光，曲昭伟.交通波理论在交叉口交通流分析中的应用 [J].中国公路学报，2002，15(1):93- 96．

WANG Dian-hai，JING Chun-guang，QU Zhao-wei.Application of traffic-wave theory in intersections traffic flow analysis [J].China Journal of Highway and Transport，2002，15(1):93- 96．

[5] COMERT G，CETIN M.Queue length estimation from probe vehicle location and the impacts of sample size [J].European Journal of Operational Research，2009，197(1):196- 202．

[6] HAO P，BAN X.Vehicle queue location estimation for signalized intersections using sample travel times from mobile sensors [C]∥Transportation Research Board of the 90th Annual Meeting.[S.l.]:TRB，2011．

[7] CHENG Y，QIN X，JIN J，et al.Cycle-by-cycle queue length estimation for signalized intersections using sampled trajectory data [J].Transportation Research Record:Journal of the Transportation Research Board，2011，2257(1):87- 94．

[8] BAN X，HAO P，SUN Z.Real time queue length estimation for signalized intersections using travel times from mobile sensors [J].Transportation Research Part C:Emerging Technologies，2011，19(6):1133- 1156．

[9] GOODALL N J，PARK B，SMITH B L.Microscopic estimation of arterial vehicle positions in a low-penetration-rate connected vehicle environment [J].Journal of Transportation Engineering，2014，140(10):04014047/1- 9．

[10] 郭谨一，刘爽，陈绍宽，等.基于Synchro的感应信号控制交叉口仿真研究 [J].交通运输系统工程与信息，2004，4(4):68- 71．

GUO Jin-yi，LIU Shuang，CHEN Shao-kuan，et al.Study on actuated signal controlled intersection a synchro-based [J].Journal of Transportation Systems Engineering and Information Technology，2004，4(4):68- 71．

[11] 邵锦锦，陈锋，孙欣欣，等.多相位感应控制配时方案的优化设计 [J].计算机系统应用，2011，20(1):48- 51．

SHAO Jin-jin，CHEN Feng，SUN Xin-xin，et al.Optimization design of multi-phase inductive control plan [J].Computer Systems & Applications，2011，20(1):48- 51．

[12] 王正武，夏利民，罗大庸.单交叉口自适应公交优先控制 [J].中国公路学报，2010，23(4):84- 90．

WANG Zheng-wu，XIA Li-min，LUO Da-yong.Adaptive transit priority control at isolated intersection [J].China Journal of Highway and Transport，2010，23(4):84- 90．

[13] 李鹏凯，杨晓光，吴伟，等.车路协同环境下信号交叉口车速引导建模与仿真 [J].交通信息与安全，2012，30(3):136- 140，156．

LI Pengkai，YANG Xiaoguang，WU Wei，et al.Modeling vehicle speed guidance at signalized intersections under IntelliDriverSM [J].Journal of Transport information and Safety，2012，30(3):136- 140，156.

[14] FORTELLE A D L.Analysis of Reservation Algorithms for Cooperative Planning at intersections [C]∥Proceedings of the 13th International IEEE Annual Conference on intelligent Transportation Systems.New York:IEEE，2010:445- 449．

[15] FENG Y，HEAD K L，KHOSHMAGHAM S，et al.A real-time adaptive signal control in a connected vehicle environment [J].Transportation Research Part C，2015，55:460- 473．