数学思想方法在有理数中的体现与应用
2017-05-27罗正刚
罗正刚
中图分类号:G632 文献标识码:C 文章编号:1672-1578(2017)05-0107-01
数学思想方法是人们对数学科学研究的本质及规律的深刻认识,它是指导学习数学,解决数学问题的思维方式、观点、策略和指导原则。它具有导向性、统摄性、迁移性的特点,它直接支配着数学的实践活动。有理数是整个代数的基础,有理数的运算是中学数学的基本运算,它所蕴涵的丰富内容深刻地反映了中学阶段许多重要基本数学思想方法。
下面,本文就结合《全日制数学课程标准》中“有理数”的有关内容谈谈数学思想方法在教学的运用。
1 数形结合思想
“数形结合”是把比较抽象的代数问题与适当的图形结合起来借助形象思维去认识、处理问题的一种思想方法。
“数无形、少直观,形无数,难入微”,利用数形结合,可以将问题化难为易,化繁为简,便于学生直观理解,并提高形象思维能力。
数轴上的点表示有理数就是最简的数形结合思想的运用,它对于学生理解有理数的相反数概念、经验值概念,有理数大小的比较,以及有理数的加法,有理数的乘法等都有重要的帮助。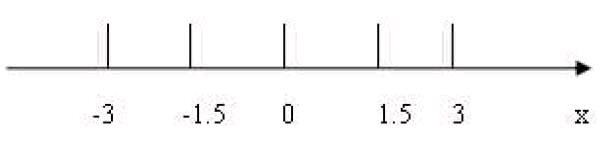
例如:“只有符号不同的两个数叫做互为相反数”。若学生从形式上强行记忆概念,很难真正理解何为相反数。现在运用数轴(如图),在数轴上画出-3与3、-1.5与1.5所有对应的点,然后引导学生观察这些点所在的位置特征,可以看到,表示为相反数的两个点,分别位于原点的两旁,且它们离原点的距离相等,这样学生就有了形象的认识,且它们离原点的距离相等,这样学生就有了形象的认识,不难理解了。这种由数想形、以形助数的方法不仅能提高学生的数形转换能力,还能提高学生的迁移思维能力。
2 化归思想
所谓“化归”就是将所要解决的复杂问题转化归结为另一个较易解决的简单问题或已经解决的问题。具体地说,就是把“新知识”转化为“旧知识”,把“复杂”转化为“简单”,这样学生学习时就容易理解和掌握了。
有理楼的知识上有许多地方都蕴藏着“化归”的思想。而在有理数运算中体现的最为突出。有理数的运算都是先确定符号,再计算绝对值,在符号确定以后,绝对值的计算实际上就是小学所学过的数的运算问题。
例如:计算:① -10+(-3), ② -10-(-7), ③ (-3)÷1/2
解:① -10+(-3)
=-(10+3)(有理数加法转化小学所学的加法)
② -10-(-7)
=-10+7(有理数减法转化为有理数加法)
=-(10-7)(有理数加法转化为小学所学的运算)
③ (-3)÷1/2
=(-3)×2(有理数除法转化为有理数乘法)
=-(3×2)(有理数乘法转化小学所学乘法)
可见,数学中利用化归思想方法,可以另辟蹊径,解决新问题,获得新知识。教师若能在此章教学中,不失时机地对学生加以启迪强化其化归思维意识,那么在今后学习代数式的运算、解方程、函数变形等知识时,运用化归思想会更加意识化。
3 分类思想
分类思想是一种逻辑划分,它把数学对象划分为不同的情形,分别进行研究,它是数学发现的重要手段。由于很多数学问题存在一些“不确定因素”,很難用“统一的标准”去解决,因此,必须把数学问题划分成“块”,然后针对不同的“块”采取相应的解决办法。可以说,分类讨论的策略是“化整为零”,各个击破。
在文章中对相反数、绝对值的概念都是运用了。分类讨论的思想方法研究的。
例如,有理数的绝对值概念是从正数、负数、零三个方面讨论。
(1)一个正数的绝对值是它本身。
(2)一个负数的绝对值是它的相反数。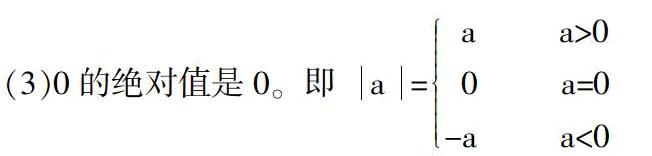
(3)0的绝对值是0。即 a= a a>0 0 a=0-a a<0
分类讨论思想不仅运用在本章的概念中,而且还多次运用在有理数的运算中。
例如,有理数的加法法则就是通过四种情形的讨论而概括出来的。
①同号两数相加,结果取相同的符号,并把绝对值相加(这里的同号又分为两加数同为正数或同为负数的情形)。
②绝对值不等的异号两数相加,结果取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
③绝对值相等的异号两数相加(即互为相反数的两数相加)结果为0。
④任何一个有理数与0相加结果仍得这个数。
另外,有理数的乘法、除法及乘方法则都是运用分类讨论思想概括的。
由以上可以看到,数学思想方法在有理数中有了一些体现,这就要求我们以此为效载体加强数学思想方法教学。在教学中笔者体会到:在数学教学中有目的渗透教学思想方法并让学生逐步领悟、掌握和学会运用数学思想方法,学生便可本质地学数学、做数学、用数学。
