现金流量折现模型应用中的常见错误及改进
2017-05-27唐秀球
唐秀球

摘 要:現金流量折现模型在本科教材《财务管理学》的证券估值和投资决策部分得到广泛的应用,但出现了一些问题与错误。对这些错误进行整理,并对其改进提出建议,以期能够给广大学生的学习带来帮助。
关键词:现金流;折现率;风险
中图分类号:F820 文献标志码:A 文章编号:1673-291X(2016)31-0077-02
现金流量折现模型是常用的价值评估模型之一,在本科教材《财务管理学》中得到广泛的应用,特别是在证券估值和投资决策中。但笔者在教授《财务管理学》的过程中发现以下问题或错误,现提出来与大家讨论,希望能给学生的学习带来一定的帮助。
一、混淆按期付息与按期计息
在人大版《财务管理学》第六版和第七版教材中,在第二章的债券估值部分,有一关于债券现值问题的例题,其资料及解题过程如下:
A公司拟购买另一家公司发行的公司债券,该债券面值为100元,期限五年,票面利率为10%,按年计息,当前市场利率为8%,该债券发行价格为多少时,A公司才能购买?
教材中的计算过程是:
PV=100×10%×PVIFA 8%,5+100×PVIF 8%,5=107.9
很显然,该题的求解过程是错误的,它混淆了按期付息与按期计息的区别。所谓按期计息,是经过一个计息期只是计算了利息,但并没有支付利息;而按期付息是每经过一个计息期就需要支付一个计息期的利息。
教材中的这种计算方法显然只是适合于按期付息的情形,五年中每年年末收到100×10%的利息构成一个期限为五年和每年年末金额为10的年金,五年末再收到本金100,所以PV=100×10%×PVIFA 8%,5+100×PVIF 8%,5=107.9 。
该例题是按期计息,其实质是:每年计息,利率为10%,计算其五年后的终值,再按市场利率为8%计算其现值,债券的现值计算应为:
PV=100×FVIF 10%,5×PVIF 8%,5=100×1.611×0.681=109.7
二、对股票估值实际报酬率的误解
在人大版《财务管理学》第六版和第七版教材中,在第二章优先股估值部分,该书是这样陈述优先股的估值:如果优先股每年支付股利分别为D,N年后被公司以每股P元的价格回购,股东要求的年必要报酬率为R,则优先股的价值为:V=D×PVIFAR,N+P×PVIFR,N,如果优先股按季度支付股利,其价值计算为:V=D×PVIFA (R/4),4N+P×PVIF (R/4),4N。
该书有一相关的例题,其资料及解题过程如下:
B公司的优先股每季度分红每股2元,二十年后,B公司必须以每股100元的价格回购这些优先股,股东要求的必要报酬率为8%,则该优先股当前的市场价值应为:V=D×PVIFA (8%/4),80+P×PVIF (8%/4),80。按照其前面对优先股估值的陈述,如果是每年支付股利,其价值应为V=D×PVIFA 8%,20+P×PVIF 8%,20。
很显然,这种分析及解决问题的过程是错误的,根据财务管理中风险与报酬的关系,一个理性投资者的要求必然是:高风险对应于高报酬,低风险对应于低报酬,风险与报酬要匹配;然而在例题中,却是股利支付方式的变化引起了股东要求的必要报酬率发生了改变,第一种情况下的年必要报酬率为8.24%,而第二种情形下的年必要报酬率为8%,这显然是错误的。
那么我们该如何来处理这一问题呢?笔者认为应做好三点:第一,我们应根据公司购买的优先股风险的大小、当前的通货膨胀率和纯利率来确定它的预估必要报酬率,根据预估必要报酬率和公司的资金成本率来确定公司的年实际必要报酬率,然后将年实际必要报酬率换算为每期的实际报酬率;第二,确定现金流;第三,使用折现模型计算优先股的价值。
为了计算方便,我们假定:根据例题里公司购买的优先股风险的大小、当前的通货膨胀率、纯利率和资金成本率确定的实际报酬率为每季2%;如果股利为每季支付2元,那么优先股的价值为:
V=D×PVIFA2%,80+P×PVIF 2%,80
如果股利是每年年末支付8元,则年实际报酬率为:
i=(1+2%)×(1+2%)×(1+2%)×(1+2%)-1=8.24%
优先股的价值变为:V=D×PVIFA8 。24%,20+P×PVIF8 。24%,20 。
三、风险投资概率法应用的错误
在一般的本科《财务管理学》教材中,是这样陈述在风险投资中的概率法,概率法是通过发生的概率来调整各期的现金流量,并计算投资项目的各期期望现金流量和期望净现值,进而对风险投资做出评价的一种方法,适用于各期现金流量相互独立的投资项目。
运用概率法时,各年的期望现金流量计算公式为:
NCFt=■NCFtiPti
NCFt——第t年的期望净现金流量;NCFti——第t年的第i种结果的净现金流量;Pti——第t年的第i种结果的发生概率;n——第t年可能结果的数量。
教材中有一相关的例题,其具体资料及解题过程如下:
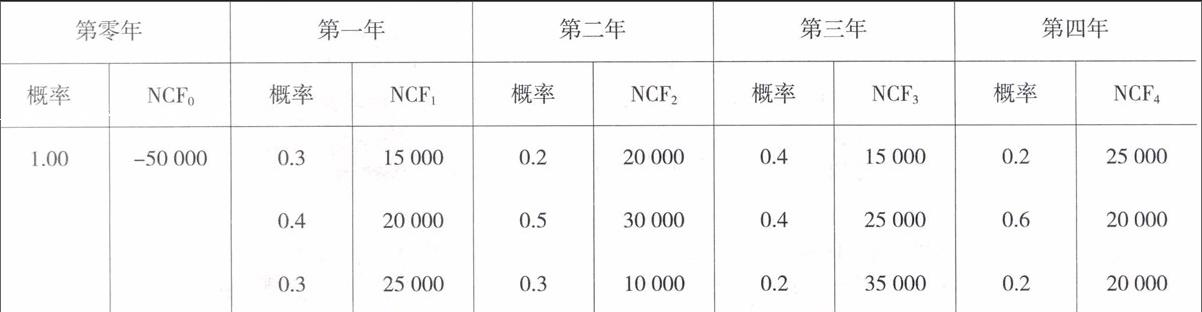
某公司的一个投资项目各年的现金流量及发生的概率情况(如下表所示),公司的资本成本率为16%。试判定此项目是否可行。
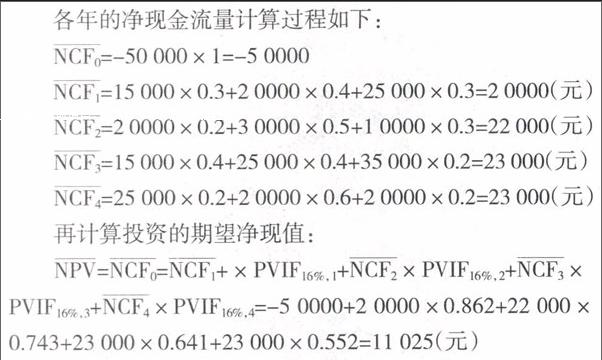
各年的净现金流量计算过程如下:
NCF0=-50 000×1=-5 0000
NCF1=15 000×0.3+2 0000×0.4+25 000×0.3=2 0000(元)
NCF2=2 0000×0.2+3 0000×0.5+1 0000×0.3=22 000(元)
NCF3=15 000×0.4+25 000×0.4+35 000×0.2=23 000(元)
NCF4=25 000×0.2+2 0000×0.6+2 0000×0.2=23 000(元)
再计算投资的期望净现值:
NPV=NCF0=NCF1+×PVIF16%,1+NCF2×PVIF16%,2+NCF3×
PVIF16%,3+NCF4×PVIF16%,4=-5 0000+2 0000×0.862+22 000×0.743+23 000×0.641+23 000×0.552=11 025(元)
因为计算出来的期望净现值大于0,所以可以进行投资。
很显然,教材对这个问题的陈述及对例题的解答过程会误导学生的学习。在对概率法的陈述及整体例题的求解过程中,先是计算每年的期望现金流,再根据公司的资金成本率计算其净现值,我们根本看不到风险对投资项目的影响。
在风险投资决策中,公司在确定项目的可行性时,有两种途径把风险对投资项目的影响考虑进去,一是把风险对投资项目的影响计入到折现率中,在无风险折现率的基础上,加上一个风险报酬率,来确定折现率;二是把风险对投资项目的影响计入到现金流,在预估每期现金流的基础上,乘以一个约当系数(风险越大,系数越小),调整每期的现金流。而上述例题的解答过程中,既没有因为风险而调整现金流,也没有因为风险而调整折现率,所以是有问题的。
那么该如何来完善这个问题呢?当然也是两种途径:一是根据风险调整折现率;二是根据风险调整每期的现金流。现在我们假定:考虑社会平均报酬率、公司的资金成本率及公司自身对该项投资风险的分散能力等因素,确定折现率为20%,则投资项目的价值为:
NPV=NCF0+NCF1×PVIF20%,1+NCF2×PVIF20%,2+NCF3×
PVIF20%,3+NCF4×PVIF20%,4=-5 0000+2 0000×0.833+22 000×0.694+23 000×0.579+23 000×0.482=6 331(元)
净现值大于零,可以投资。
四、小结
从以上几个常见的错误可以看出,在现金流量折现模型的应用中,要准确把握二个问题,即现金流和折现率,现概括如下:第一,对于确定性投资决策而言,其现金流是确定的,但我们必须弄清楚现金流流入和流出的准确时点,其折现率的确定需要考虑的因素有纯利率、通货膨胀补偿和公司的资金成本率。第二,对于风险性投资决策而言,首先是预估现金流和折现率,其次是如何处理风险。对于风险的处理,一種途径是根据风险的大小调整现金流,另一种是根据风险的大小调整折现率,公司在评估投资项目的可行性时,必须两者选择其一。第三,对于风险性投资决策,在评估投资项目的风险时,还要考虑该公司对投资项目风险的分散能力,只考虑无法分散的那部分风险的影响,以此调整现金流或者折现率。第四,无论是确定性投资决策,还是风险性投资决策,对于给出的实际报酬率的期限与现金实际流入流出的期限不一致的情形,一定要按实际利率必须相等来换算,确定每期的折现率,如本文中优先股给出的实际报酬率是每季2%,换算为年实际报酬率为每年8.24%(也就是年折现率),而不是每年8%。
参考文献:
[1] 荆新,王化成,刘俊彦.财务管理学[M].北京:中国人民大学出版社,2015.
