自旋轨道耦合驱动下二维质量不相等费米气体的拓扑相
2017-05-25张鹏梁军军
张鹏,梁军军
(山西大学 理论物理研究所,山西 太原 030006)
自旋轨道耦合驱动下二维质量不相等费米气体的拓扑相
张鹏,梁军军*
(山西大学 理论物理研究所,山西 太原 030006)
用平均场理论研究了二维质量不相等费米气系统的零温特性,该系统具有equal-Rashba-Dresselhaus (ERD)型自旋轨道耦合作用和Zeeman场。在该系统中存在三种不同的超流相(US-0相、US-1相、US-2相),我们通过数值分析能隙方程和粒子数方程组成的自洽方程组,发现二维费米气系统的质量相差越大,Zeeman场对超流序参量Δ的抑制作用就会越强。在弱吸引相互作用区域,随着自旋轨道耦合强度的增加,US-2拓扑超流相会逐渐收缩。自旋轨道耦合强度一定情况下,质量比0<λ≤1时,只有在弱吸引相互作用区域存在US-2拓扑超流相;当质量比λ>1时,在弱相互作用区域和强相互作用区域都存在US-2拓扑超流相。
费米气体;自旋轨道耦合(SOC);质量不相等;拓扑相
0 引言
近年来,实验上利用拉曼光来耦合费米气体超精细态从而可以模拟人工规范场,由此引起人们对冷原子中拓扑相变理论的广泛关注。人们在理论上提出了利用冷原子气体来实现自旋轨道耦合的多种方案,但在实验上目前只实现了等量的Rashba-Dresselhaus自旋轨道耦合。受到该实验的启发,越来越多的人开始研究在自旋轨道耦合、Zeeman场以及原子间相互作用等可调参数驱动下冷原子的低温量子特性[1-8,11-14]。
平均场理论揭示了该Zeeman场存在时自旋轨道耦合会引起非拓扑超流相到拓扑超流相的量子相变[4]。自旋轨道耦合可以增加超流序参量的配对,而Zeeman场可以抑制超流序参量的配对。本文主要考虑两组分的费米气体约化质量不同的情况。通过把等质量两组分费米气载入与自旋相关的光学晶格,就使得不同组分具有不同的约化质量[9]。下面我们用平均场理论来讨论各种拓扑超流相的量子相变。
1 平均场理论
考虑一个二维质量不相等的费米冷原子气系统,其同时具有equal-Rashba-Dresselhaus (ERD)型自旋轨道耦合作用和沿着z方向的Zeeman场。这种系统的Hamilton量有如下表示形式:
(1)
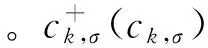
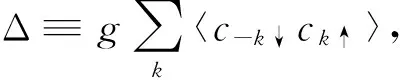
(2)
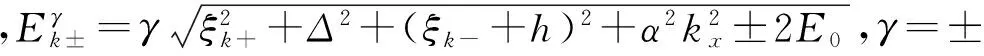
(3)
由∂Ω/∂Δ=0和N=-∂Ω/∂μ,可以得到能隙方程和粒子数方程:
(4)
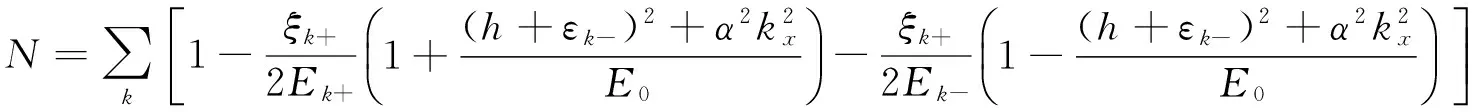
(5)
得到由能隙方程和粒子数方程组成的自洽方程组后,便可以通过数值求解来分析Zeeman场对超流序参量Δ的影响,接下来我们讨论拓扑超流相的分类条件。
2 拓扑超流相的分类

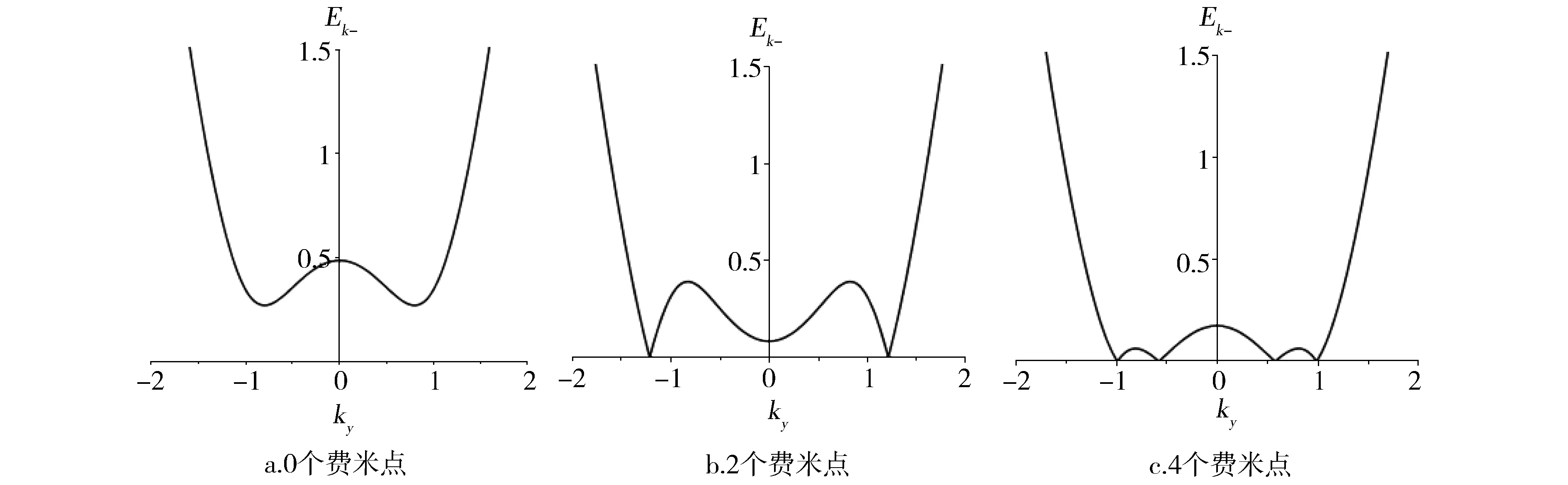
Fig.1 Three kinds of topologically distinct superfluid (US) phases图1 三种不同的拓扑超流相
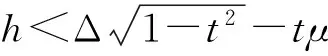
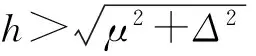
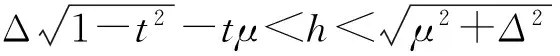
利用上面拓扑超流相的分类条件,就可以通过数值求解自洽方程组来研究不同质量比随Zeeman场变化的零温相图,以及某一质量比下两体束缚能随Zeeman场变化的零温相图。
3 数值计算
为了计算的方便,我们将对前面的能隙方程(4)和粒子数方程(5)组成的自洽方程组进行无量纲化。需做以下变换
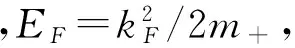
(6)
(7)
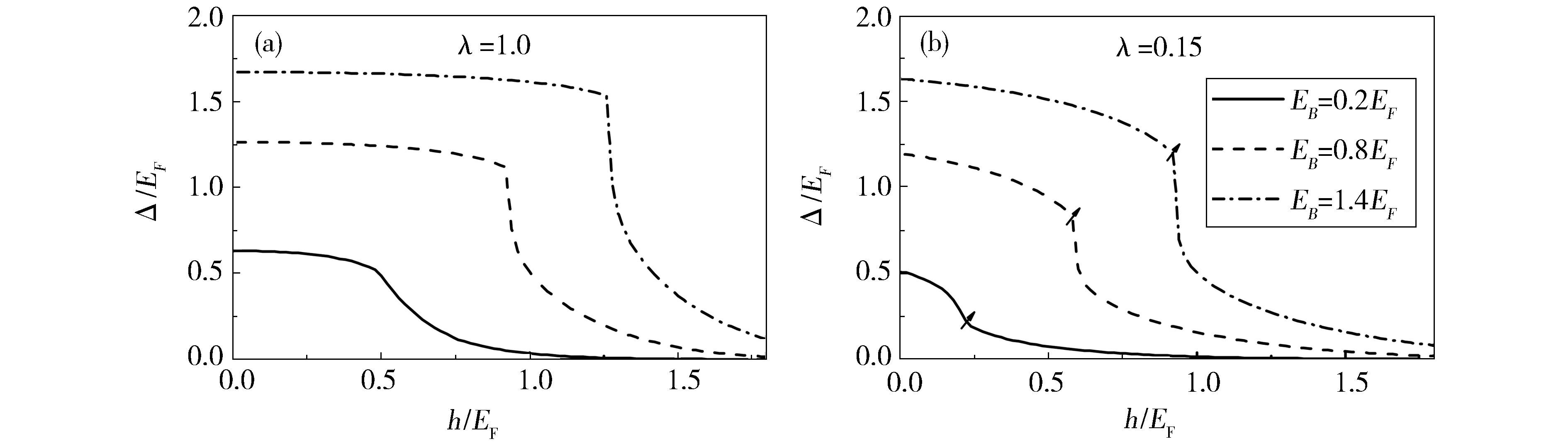
Fig.2 Order parameter Δ as a function of the Zeeman field h at the ERD SOC αkF/EF=1.0 for different values of the two-body binding energy. (a) mass radio λ=1.0, (b) mass radio λ=0.15(a)质量比λ=1.0,(b)质量比λ=0.15图2 ERD自旋轨道耦合强度为αkF/EF=1.0,两体束缚能取不同的值时,序参量Δ随Zeeman场h的变化关系
首先通过数值求解自洽方程组来研究质量不相等时,Zeeman场对超流序参量Δ的影响。从图2(a)、(b)两图的比较中我们发现二维费米气系统的质量相差越大(质量比越小),Zeeman场对超流序参量Δ的抑制作用就会越强。只要给定一个两体束缚能的值,就会有一个Zeeman场的临界值存在,在此处发生一级相变。图4(b)中箭头表示一级相变的位置。

Fig.3 Phase diagrams of a 2-D Fermi gas with two-body binding energy EB/EF=0.2 at zero temperature.SOC αkF/EF=1.0, Zeeman field h versus reduced mass radio m+/m-自旋轨道耦合αkF/EF=1. 0时,Zeeman场h随约化质量比m+/m-变化的相图图3 两体束缚能为EB/EF=0.2的二维费米气零温相图
接着数值求解自洽方程组并结合拓扑超流相变的条件,得到不同约化质量比随Zeeman场变化的零温相图。这里需要强调的是质量比λ=m↑/m↓,其取值范围为λ>0。为了研究的方便我们将无穷区间转化为有限区间,用约化质量比t来替代质量比λ。由m±=m↑m↓/(m↑±m↓),t=m+/m-,可以得到约化质量比的范围-1 图3中可以看出两体束缚能为EB/EF=0.2,即在弱吸引相互作用下,系统在绝大部分范围内都经历了两次超流相变:US-0→US-2→US-1,很小范围内会发生US-0→US-1相变。通过增加自旋轨道耦合强度,还发现随着自旋轨道耦合强度的增加,US-2拓扑超流相会逐渐收缩。 前面讨论了不同约化质量比随Zeeman场变化的相图。接下来要研究约化质量比为t=0.739与t=-0.739费米气的两体束缚能随Zeeman场变化的相图。 图4(a)中当约化质量比t=0.739时,只有在弱吸引相互作用区域存在US-2拓扑超流相。t→0时,US-2相在弱吸引相互作用区域范围会变大,t→1时,US-2相在弱吸引相互作用区域范围会变小。图(b)中当约化质量比t=-0.739时,在弱相互作用区域和强相互作用区域都会存在US-2拓扑超流相。t<0时,US-2相开始在强吸引相互作用区域出现,t→-1时,US-2相在强吸引相互作用区域范围会变大。因此,我们发现当约化质量比0≤t<1时,只有在弱吸引相互作用区域存在US-2拓扑超流相;当-1 (a) Reduced mass radio t=0.739, Zeeman field h versus binding energy EB(b) Reduced mass radio t=-0.739, Zeeman field h versus binding energy EBFig.4 Phase diagrams of a 2-D Fermi gas with ERD SOC αkF/EF=1.0 at zero temperature(a)约化质量比t=0.739,Zeeman场h随束缚能EB的变化关系(b)约化质量比t=-0.739,Zeeman场h随束缚能EB的变化关系图4 ERD自旋轨道耦合强度为αkF/EF=1.0的二维费米气零温相图 本文应用平均场理论研究二维质量不相等的ERD型SOC费米气的零温特性,我们发现二维费米气系统的质量相差越大,Zeeman场对超流序参量Δ的抑制作用就会越强,只要给定一个两体束缚能的值,就会有一个Zeeman场的临界值存在,此处为一级相变点。在弱吸引相互作用区域,随着自旋轨道耦合强度的增加,US-2拓扑超流相会逐渐收缩。自旋轨道耦合强度一定的情况下,当质量比0<λ≤1时,只有在弱吸引相互作用区域存在US-2拓扑超流相;当质量比λ>1时,在弱相互作用区域和强相互作用区域都会存在US-2拓扑超流相。 [1] Devreese J P A,Tempere J,Melo C A R S D.Quantum Phase Transitions and Berezinskii-Kosterlitz-Thouless Temperature in a Two-dimensional Spin-orbit-coupled Fermi Gas[J].PhysicalReviewA,2015,92(4).DOI:10.1103/PhysRevA.92.043618. [2] Shi H,Rosenberg P,Chiesa S,etal.Rashba Spin-Orbit Coupling,Strong Interactions,and the BCS-BEC Crossover in the Ground State of the Two-Dimensional Fermi Gas[J].PhysicalReviewLetters,2016,117(4).DOI:10. 1103/PhysRevLett.117.040401. [3] Chen G,Gong M,Zhang C.BCS-BEC Crossover in Spin-orbit Coupled Two-dimensional Fermi Gases[J].PhysicalReviewA,2011,85(1):145-149.DOI:10.1103/PhysRevA.85.013601. [4] Wu F,Guo G C,Zhang W,etal.Unconventional Superfluid in a Two-dimensional Fermi Gas with Anisotropic Spin-orbit Coupling and Zeeman Fields[J].PhysicalReviewLetters,2013,110(11):1504-1509.DOI:10.1103/PhysRevLett.110.110401. [5] Yang X,Wan S.Phase Diagram of a Uniform Two-dimensional Fermi Gas with Spin-orbit Coupling[J].PhysicalReviewA,2011,85(85):5809-5816.DOI:10.1103/PhysRevA.85.023633. [6] Gong M,Tewari S,Zhang C.BCS-BEC Crossover and Topological Phase Transition in 3D Spin-orbit Coupled Degenerate Fermi Gases[J].PhysicalReviewLetters,2011,107(19):3096-3100.DOI:10.1103/PhysRevLett.107.195303. [7] Jiang L,Liu X J,Hu H,etal.Rashba Spin-orbit Coupled Atomic Fermi Gases[J].PhysicalReviewA,2011,84(6):1872-1874.DOI:10.1103/PhysRevA.84.063618. [8] Seo K,Han L,Ca S D M.Emergence of Majorana and Dirac Particles in Ultracold Fermions Via Tunable Interactions,Spin-orbit Effects,and Zeeman Fields[J].PhysicalReviewLetters,2012,109(10):2523-2527.DOI:10.1103/PhysRevLett.109.105303. [9] Iskin M,Subasi A L.Mass-imbalanced Fermi Gases with Spin-orbit Coupling[J].PhysicalReviewA,2011,84(4):1504-1512.DOI:10.1103/PhysRevA.84.041610. [10] Iskin M,Subasi A L.Stability of Spin-orbit Coupled Fermi Gases with Population Imbalance[J].PhysicalReviewLetters,2011,107(5):6629-6636.DOI:10.1103/PhysRevLett.107.050402. [11] Tewari S,Stanescu T D,Sau J D,etal.Topologically Non-trivial Superconductivity in Spin-orbit Coupled Systems:Bulk Phases and Quantum Phase Transitions[J].NewJournalofPhysics,2010,13(6):543-586.DOI:10.1088/1367-2630/13/6/065004. [12] He L,Lv H,Cao G,etal.Quantum Fluctuations in the BCS-BEC Crossover of Two-dimensional Fermi Gases[J].2015,92(2):023620.DOI:10.1103/PhysRevA.92.023620. [13] Iskin M,Subasi A L.Topological Superfluid Phases of an Atomic Fermi Gas with in- and Out-of-Plane Zeeman Fields and Equal Rashba-Dresselhaus Spin-orbit Coupling[J].PhysicalReviewA,2012,87(6):944-948.DOI:10.1103/PhysRevA.87.063627. [14] Hu H,Liu X J.Mean Field Phase Diagrams of Imbalanced Fermi Gases Near a Feshbach Resonance[J].PhysicalReviewA,2006,73(5):180-180.DOI:10.1103/PhysRevA.73.051603. Topological Phase in a Two-dimensional Mass-imbalanced Fermi Gases Driven by Spin-orbit Coupling ZHANG Peng,LIANG Junjun* (Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China) We use the mean-field theory to investigate zero temperature characteristic in a two-dimensional (2-D) mass-imbalanced Fermi gases with equal-Rashba-Dresselhaus (ERD) spin-orbit coupling (SOC) and Zeeman field. The system exists three topologically distinct superfluid phases (US-0 phase, US-1 phase, US-2 phase). Through analying the gap and atom number equations numerically, we find that superfluid order parameter can be suppressed more stronger by a Zeeman field as the mass difference increases. With increasing SOC, the weak atractive interaction region of the US-2 phase shrinks. When there is a finite SOC of the ERD type, 0<λ<1,only in the weak atractive interaction region US-2 topologically superfluid phases exists;λ>1,in weak and strong atractive interaction region US-2 topologically superfluid phases exists. Fermi gases;spin-orbit coupling(SOC);mass-imbalanced;topological phase 10.13451/j.cnki.shanxi.univ(nat.sci.).2017.02.015 2016-11-17; 2017-01-10 国家自然科学基金(11005071) 张鹏(1988-),男,太原人,在读硕士,研究方向:超冷费米气体,E-mail:zhpeng2016phy@163.com *通信作者:梁军军(LIANG Junjun),E-mail:liangjj@sxu.edu.cn O413 A 0253-2395(2017)02-0300-05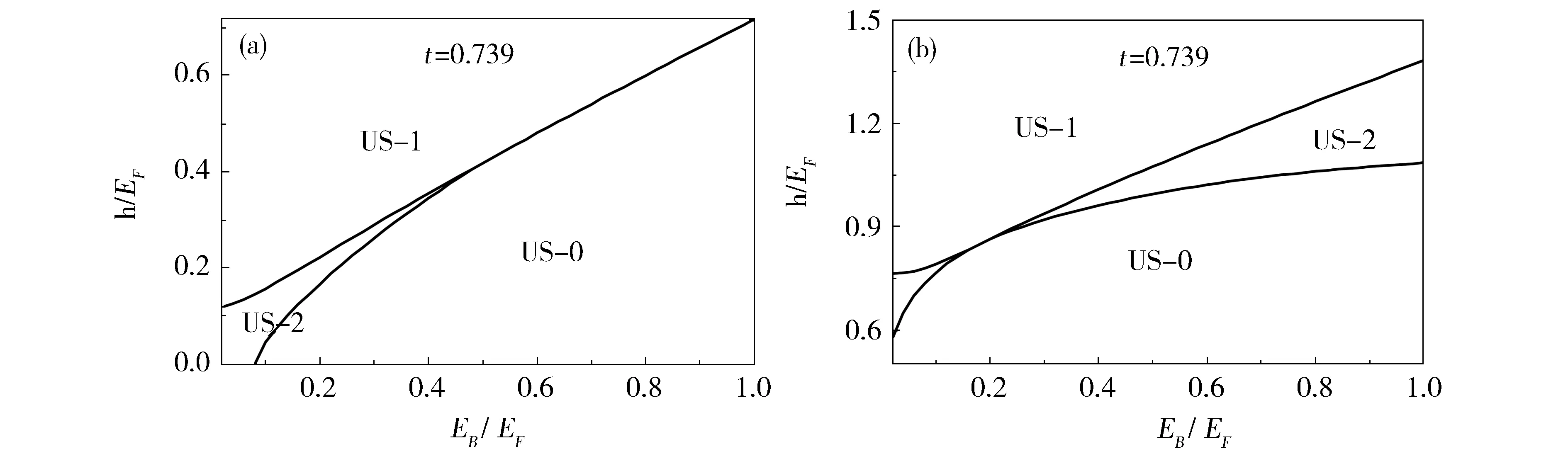
4 结论
