用于连续变量码率自适应的数据协调方案
2017-05-25白增亮杨申申李永民
白增亮,杨申申,李永民
(山西大学 光电研究所 量子光学与光量子器件国家重点实验室,山西 太原 030006;山西大学 极端光学协同创新中心,山西 太原 030006)
用于连续变量码率自适应的数据协调方案
白增亮,杨申申,李永民*
(山西大学 光电研究所 量子光学与光量子器件国家重点实验室,山西 太原 030006;山西大学 极端光学协同创新中心,山西 太原 030006)
量子密钥分发能够使得合法通信双方共享一组无条件安全的密钥。数据协调是量子密钥分发过程中非常重要的一个环节,能够对密钥分发过程中产生的错误进行纠错。低密度奇偶校验(LDPC)码是一种性能接近于Shannon极限的信道纠错码,适用于高效的数据协调。为了达到高的协调效率,需要根据信道的信噪比适当地选择最佳的LDPC码的码率。我们提出了一种适用于高斯调制连续变量量子密钥分发的码率可调的数据协调方案:当信道信噪比发生变化时,使用码率调整技术对数据协调过程中每一级LDPC码的码率进行适当地调整,从而确保数据协调的效率在一定信噪比变化范围内能够保持。
量子密钥分发;连续变量;数据协调;LDPC码;码率自适应
0 引言
量子密钥分发[1-5]是量子信息领域最接近实用化的一个发展方向,已经成为各国学者的研究热点之一。基于量子物理的基本原理(量子不确定性原理和量子不可克隆定理),任何潜在的窃听者都会对量子态造成扰动,量子密钥分发能够对任意的窃听行为进行检测。共享的密钥用于一次一密(one-time pad)加密方案,通信双方可以实现无条件的安全通信。由于其具有安全通信的优势,能够广泛用于国防、军事、商业等领域。近几年量子密钥分发在实验室已经取得快速的发展,逐步走向了工程化、产品化阶段。
量子密钥分发一般包括量子密钥传输和经典的数据后处理两个阶段。在第一个阶段,通信双方(Alice和Bob)将密钥信息通过量子信道传输获得裸码。离散变量量子密钥分发将密钥信息调制在单光子或者弱相干态上,使用单光子探测器对量子态进行测量。连续变量量子密钥分发将高斯随机数调制到相干态或者压缩态光场上,然后使用平衡零拍探测器对其进行测量。由于在量子传输过程中存在各种各样的噪声以及第三方的窃听,在数据后处理阶段需要对量子传输以后得到的裸码信息进行经典的数据处理,最终提取出无条件安全的密钥。数据后处理主要包括数据协调与私密放大两个过程。数据协调是一个纠错过程,使用信道纠错的方法对裸码中不一致的信息进行纠错。然后经过私密放大,去除窃听者窃取的信息,从部分安全的信息中提取出安全密钥。
与离散变量相比,连续变量量子密钥分发在较短距离上能够实现较高的安全密钥速率,具有易于实现的商业化光学组件以及能够较好地兼容于现有的光通信网络。针对连续变量的数据协调,主要包括样条数据协调(slice reconciliation)[6-10]和多维协调(multidimensional reconciliation)[11-13]两种方案。样条数据协调主要适用于信噪比大于1的较短距离连续变量量子密钥分发。在信道纠错过程中,采用多级编码和多级译码(Multilevel coding and Multistage decoding)方案[7]。同时采用逆向协调方案(正向协调要求量子信道传输率必须大于0.5)[14]并结合边信息(side information)译码原理[15],通信双方只进行单次通信,从而最大限度地减小了信息的泄露,实现高效的数据协调。
低密度奇偶校验码,简称LDPC码,属于信道纠错码,具有接近香农极限的纠错性能,低的误码平台以及低的译码复杂度。将LDPC码用于数据协调中,能够实现高效的数据协调。在实际密钥分发过程中信道的信噪比并不是固定不变的,而是随着时间的变化,信噪比也发生着变化。LDPC码的码率自适应方案能够随着信噪比的变化而对码率进行适当的调整,从而能够在较大的信噪比变化范围内得到高的纠错效率。对于在离散变量量子密钥分发过程中,目前已经提出了几种码率可调整的自适应纠错方案[16-18],用于连续变量量子密钥分发的码率自适应方案还未有公开的报道。本文我们提出了连续变量的码率兼容的样条数据纠错方案,能够实现多级编码中每一级的码率根据信噪比的变化进行适当的调整,从而能够更有效地进行纠错编码,实现更高效的数据协调。
1 LDPC码率调整
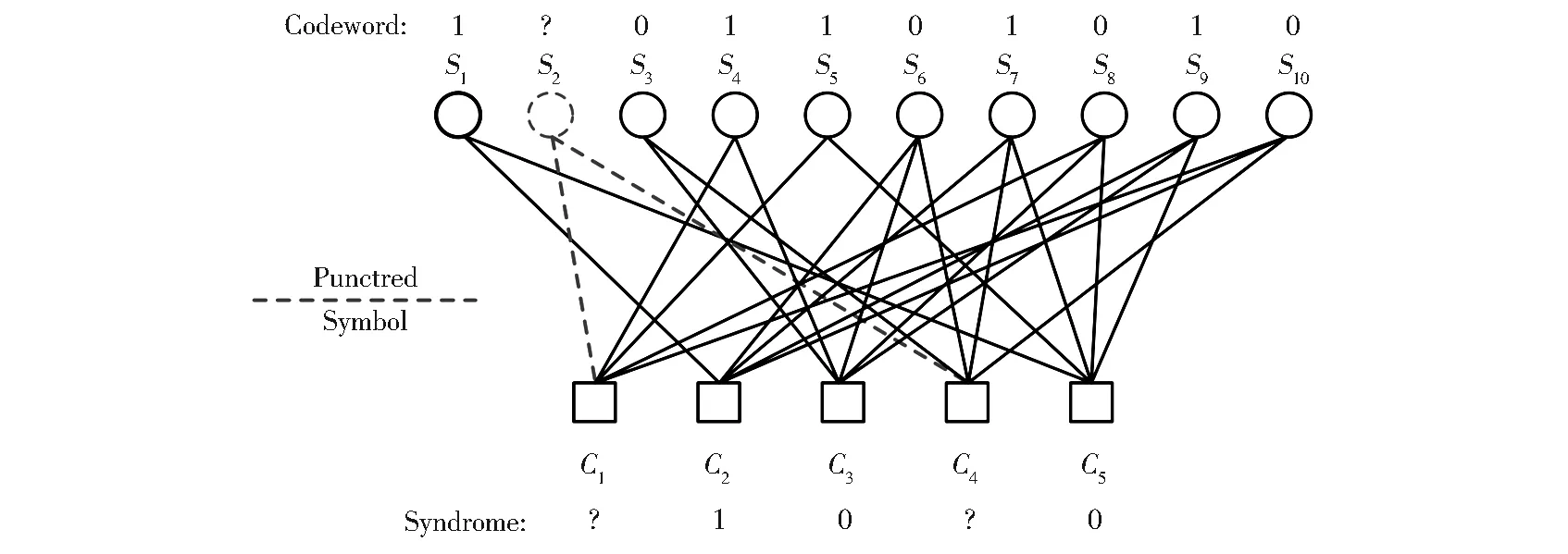
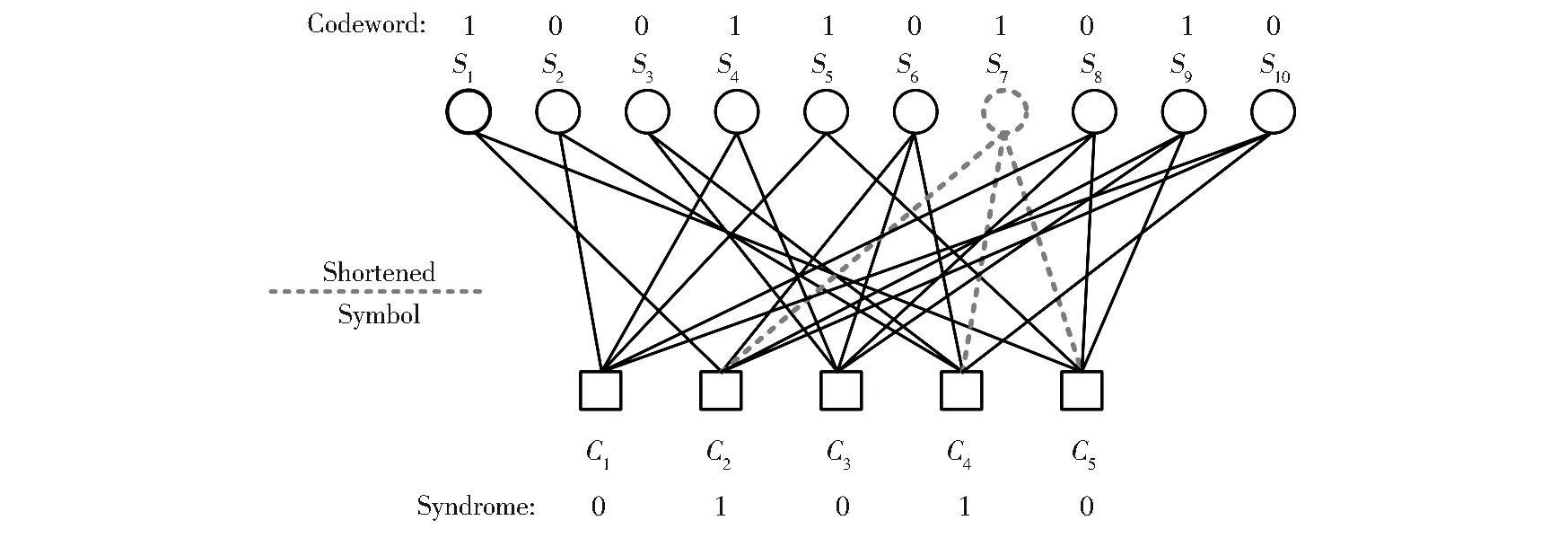
LDPC码通常利用一个稀疏的校验矩阵或者Tanner图来表示。Tanner图中采用边将校验节点和变量节点相连。基于Tanner图中不同变量节点之间的信息传递,LDPC码采用后验概率信息的软判决译码,并通过迭代运算,从而实现高的纠错性能。删余(Puncturing)[19-20]和缩短(Shortening)[21]是两种码率调整技术,能够使LDPC码的码率分别增大和减小。使用这两种技术,我们可以对信噪比变化的信道实现LDPC码码率的自适应纠错编码。给定一个预先构造好的LDPC码C(n,k), 在n个码字中删除p个符号(p (1) (2) (3) Fig.1 Scheme of puncturing applied to a LDPC code represented by its Tanner graph. si:variable node,ci:check node图1 Tanner图中LDPC码的删余方案,si:变量节点,ci:校验节点 Fig.2 Scheme of shortening applied to a LDPC code represented by its Tanner graph.si:variable node,ci:check node图2 Tanner图中LDPC码的缩短方案,si:变量节点,ci:校验节点 对于高斯调制相干态的连续变量量子密钥分发中,双方得到的裸码是一组相互关联的连续的高斯分布随机数。样条数据协调的过程中Bob首先需要对高斯分布的连续变量进行2m区间量化,转化为m级二进制的随机序列,然后对每一级二进制序列分别编码(生成校验子)并发送给Alice。Alice结合自己原有的信息对每一级接收到的信息进行联合迭代译码,最终双方能够共享相同的二进制序列。在信道纠错过程中,LDPC码只是针对某个信噪比而预先设计,无法满足信噪比连续变化的信道。我们在传统样条数据协调[10]的基础上引入了LDPC码率调整方案,可以使得预先设计的LDPC码适用于一定范围的信噪比区间。连续变量量子密钥分发码率自适应的样条数据协调过程如图3所示。 高斯随机数X和Y是Alice和Bob经过量子传输以后得到的一组相互关联的高斯随机数。双方通过信道参数估计可以计算得到量子信道的信噪比。根据信噪比选定初始的LDPC码,当信道信噪比发生较小的变化时,我们就可以使用LDPC码的删余和缩短技术对码率做适当的调整,具体步骤如下: 第二步:设定参数。信噪比发生改变后,根据当前信噪比,设定参数d(删余符号和缩短符号的数量总和)以及每一级合适的目标码率Ri。由于在多级译码过程中,每一级的译码与其他级并不是相互独立的,需要对多级之间进行联合译码,所以每一级中的参数d必须是相同的。缩短符号的数量ti和删余符号的数量pi分别可以根据以下式子计算得到: (4) pi=d-ti. (5) 第五步:多级译码。Alice对从经典信道接收到的信息采用belief propagation译码算法进行迭代译码以及多级之间联合译码。在译码过程中,Alice首先将自己原有的高斯随机数作为边信息,结合接收到的信息,对Bob端的信息进行一个初始化估算。由于Bob仅仅将删余符号的位置发送给对方,所以Alice无法估算码字中删余符号的信息。 通过以上编码和译码过程,我们就可以对初始LDPC码实现删余和缩短操作,方便灵活地改变数据协调过程中每一级码率,从而在信道信噪比变化的情况下实现高效的数据协调。 量子密钥分发由于在安全通信领域具有重要的应用价值,引起了各国研究人员的广泛研究与关注。数据协调是量子密钥分发中一个非常重要的环节,直接影响着通信双方的安全密钥速率和密钥分发距离。本文中我们在样条数据协调的基础上提出了一种基于LDPC码码率自适应的连续变量数据纠错方案,提高样条数据协调的码率兼容性,能够实现码率自适应的数据协调。该方案可以用于连续变量量子密钥分发系统中。对于该方案进一步的理论仿真,需要解决LDPC码删余过程中度分布的最优选择,长码长LDPC码的校验矩阵构造以及方案中参数d的选择确定等一系列问题,将是我们下一步的研究重点。 [1] Bennett C H,Brassard G.Proceedings of IEEE International Conference on Computers,Systems and Signal Processing,1984[C]∥Bangalore,IEEE,1984. [2] Ralph T C.Continuous Variable Quantum Cryptography[J].PhysRevA,1999,61:010303.DOI:10.1103/PhysRevA.61.010303. [3] Gisin N,Ribordy G,Tittel W,etal.Quantum Cryptography[J].RevModPhys,2002,74:145-195.DOI:10.1103/RevModPhys.74.145. [4] Braunstein S L,Van Loock P.Quantum Information with Continuous Variables[J].RevModPhys,2005,77:513-577.DOI:10.1103/RevModPhys.77.513. [5] Scarani V,Bechmann-Pasquinucci H,Cerf N J,etal.The Security of Practical Quantum Key Distribution[J].RevModPhys,2009,81:1301-1350.DOI:10.1103/RevModPhys.81.1301. [6] Van Assche G,Cardinal J,Cerf N J.Reconciliation of a Quantum-distributed Gaussian Key[J].IEEETInformTheory,2004,50:394-400.DOI:10.1109/TIT.2003.822618. [7] Bloch M,Thangaraj A,McLaughlin S W,etal.Proceedings of Information Theory Workshop,Mar.13-17,2006[C].Uruguay,IEEE,2006.DOI:10.1109/ITW.2006.1633793. [8] Lodewyck J,Bloch M,García-Patrón R,etal.Quantum Key Distribution Over 25 km with an All-fiber Continuous-variable System[J].PhysRevA,2007,76:042305.DOI:10.1103/PhysRevA.76.042305. [9] Jouguet P,Elkouss D,Kunz-Jacques S.High-bit-rate Continuous-variable Quantum Key Distribution[J].PhysRevA,2014,90:042329.DOI:10.1103/PhysRevA.90.042329. [10] Bai Z L,Wang X Y,Yang S S,etal.High-efficiency Gaussian Key Reconciliation in Continuous Variable Quantum Key Distribution[J].SciChinaPhysMechAstron,2016,59:614201-614201.DOI:10.1007/s11433-015-5702-7. [11] Leverrier A,Alléaume R,Boutros J,etal.Multidimensional Reconciliation for a Continuous-variable Quantum Key Distribution[J].PhysRevA,2008,77:042325.DOI:10.1103/PhysRevA.77.042325. [12] Jouguet P,Kunz-Jacques S,Leverrier A.Long-distance Continuous-variable Quantum Key Distribution with a Gaussian Modulation[J].PhysRevA,2011,84:062317.DOI:10.1103/PhysRevA.84.062317. [13] Jouguet P,Kunz-Jacques S,Leverrier A,etal.Experimental Demonstration of Long-distance Continuous-variable Quantum Key Distribution[J].NatPhotonics,2013,7:378-381.DOI:10.1038/NPHOTON.2013.63. [14] Grosshans F,Grangier P.Reverse Reconciliation Protocols for Quantum Cryptography with Continuous Variables[J/OL].arXiv:quant-ph/0204127v1,Apr.22,2002. [15] Liveris A D,Xiong Z X,Georghiades C N.Compression of Binary Sources with Side Information at the Decoder using LDPC Codes[J].IEEECommunLett,2002,6:440-442.DOI:10.1109/LCOMM.2002.804244. [16] Elkouss D,Martinez J,Lancho D,etal.Proceedings of IEEE Information Theory Workshop on Information Theory,Jan.6-8,2010[C].Cairo,IEEE,2010.DOI:10.1109/ITWKSPS.2010.5503195. [17] Elkouss D,Martínez-Mateo J,Martin V.Proceedings of International Symposium On Information Theory & Its Applications, Oct. 17-20,2010[C]∥Taiwan,IEEE,2010.DOI:10.1109/ISITA.2010.5650099. [18] Martinez-Mateo J,Elkouss D,Martin V.Blind Reconciliation[J].QuantumInfComput,2012,12:791-812. [19] Pishro-Nik H,Fekri F.Proceedings of Information Theory Workshop,Oct.24-29,2004[C]∥IEEE,2005.DOI:10.1109/ITW.2004.1405302. [20] Jeongseok H,Jaehong K,McLaughlin S W.Rate-compatible Puncturing of Low-density Parity-check Codes[J].IEEETInformTheory,2004,50:2824-2836.DOI:10.1109/TIT.2004.836667. [21] Tian T,Jones C R.Construction of Rate-Compatible LDPC Codes Utilizing Information Shortening and Parity Puncturing[J].EURASIPJWirelCommunNetw,2005,5:789-795.DOI:10.1155/WCN.2005.789. Rate-Adaptive Protocol for Continuous Variable Key Reconciliation BAI Zengliang,YANG Shenshen,LI Yongmin* (State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Opto-Electronics, Shanxi University, Taiyuan 030006,China;Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006,China) Quantum key distribution (QKD) enables two legal parities to share a secure key. Information reconciliation is an essential process in quantum key distribution. Low-density parity-check (LDPC) codes, which belong to the class of linear error correcting codes and perform at rates extremely close to the Shannon capacity, can achieve the key reconciliation with high efficiency. Considering a time-varying channel in practical continuous variable QKD system, we propose a rate-adaptive protocol for continuous variable key reconciliation, which can cover a broad range of signal-to-noise ratio and achieve higher reconciliation efficiency. quantum key distribution; continuous variable; information reconciliation; LDPC code; rate-adaptive 10.13451/j.cnki.shanxi.univ(nat.sci.).2017.02.012 2017-02-28; 2017-03-07 国家自然科学基金(61378010;11504219);国家重点研发计划(2016YFA0301403);山西省高等学校创新人才支持计划资助的课题 白增亮(1984-),男,博士研究生,主要从事量子通信方面的研究。E-mail:bzlwmj@foxmail.com *通信作者:李永民(LI Yongmin),E-mail:yongmin@sxu.edu.cn O431 A 0253-2395(2017)02-0281-05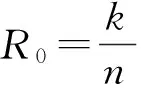
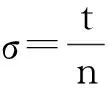
2 码率自适应的样条数据协调方案设计
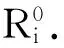
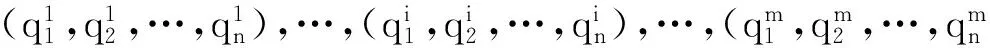
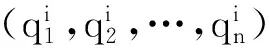
3 结论
