4种张量分解方法用于人脸识别的效果对比和分析

胡小平(安庆师范大学 计算机与信息学院，安徽 安庆 246133)

4种张量分解方法用于人脸识别的效果对比和分析

胡小平
(安庆师范大学 计算机与信息学院，安徽 安庆 246133)

张量的分解是主成分分析(PCA)在高阶上的扩展，目前几种张量分解方法各有优缺点，难以满足PCA的所有性质．基于4种经典的张量分解方法并没有在人脸识别中进行比较分析，利用ORL人脸数据库比较了4种经典的张量分解方法．实验结果表明，张量方法在压缩率大的情况下，其性能有显著的提高．不同的张量分解方法显示理论上分析Higher-Order Orthogonal Iteration (HOOI)的拟和度最好，但这4种方法用到实际人脸数据上并没有多大差别．考虑到Higher-Order Singular Value Decomposition(HO-SVD)方法相对比较简单，人脸识别研究时可选用此方法．

人脸识别；张量分解；主成分分析；张量

随着特征提取技术的发展，越来越多的特征可以采用张量的统一表示形式．传统的向量表示方法以及处理方法对于这样的特征常显得力不从心，于是研究张量的性质及运算获得广泛的关注．

张量化的数据处理面临的最大问题是如何选用合适的数学工具来对它进行分析．N-mode SVD( tensor SVD)是PCA(matrix SVD)在高阶上的扩展，最早是由Tucker等[1]提出，接着不少人对它进行了扩展，但张量的分解并不能简单地看作是PCA在高阶上的简单扩展，目前还不存在一种tensor SVD能满足matrix SVD的所有性质．并存着多种方法分解张量，这些方法都各有自己的优缺点．Lathauwer等[2]总结了使用最广泛的一种张量分解方法 HOSVD，并分析了它的相关性质及其与SVD之间的联系，接着Turney[3]总结并比较分析了当前比较流行的4种张量分解方法，分别是Higher-Order Singular Value Decomposition (HO-SVD)[2]，Higher-Order Orthogonal Iteration (HOOI)[4]，Slice Projection (SP)[5]和 Multislice Projection(MP)[3]．因人脸是一种高维、复杂的模式，其特征呈现出张量的模式．随着张量技术的发展，张量逐渐应用到人脸领域，Vasilescu等[6-7]将多线性分析引入到人脸识别中，使用张量代数对人脸进行分析，提出了张量的多线性投影方法和Tensorfaces方法．不少研究者[8-11]也在此基础上改进了张量方法，如Cao等[12]将张量代数用于人脸聚类．

不同张量分解方法对人脸识别效果的影响是不一样的，HO-SVD, HOOI, SP都曾用于人脸识别，但MP还未用于人脸识别，这几种方法都没有在人脸识别中进行比较分析．周春光等[13]在多线性主成分分析的基础上提出了基于稀疏张量的人脸图像特征提取方法．本文在ORL人脸库中结合3D-PCA[14]对这4种张量分解方法对人脸识别效果进行比较分析，并总结出可用于人脸识别研究用的较好的方法．

1 4种张量分解法

一般把张量视为多维数组，是0维标量、1维向量和2维矩阵的n维推广，可以用来表达多线性概念的某种确定类型．在张量的概念里，把张量的维数称为阶数，如标量是0阶张量，向量是1阶张量，矩阵是2阶张量．一般情况下，维数有2个概念，一个指的是一个向量的自由度，即一个向量的分量个数；另一个跟阶数是一个意思，如2维矩阵，3维矩阵等．为了不造成概念混乱，后面用维数表示一个向量的自由度，而用阶表示维数．

通过展开张量A和Z， 可以得到“N-mode SVD”的矩阵表示如公式(1)所示．

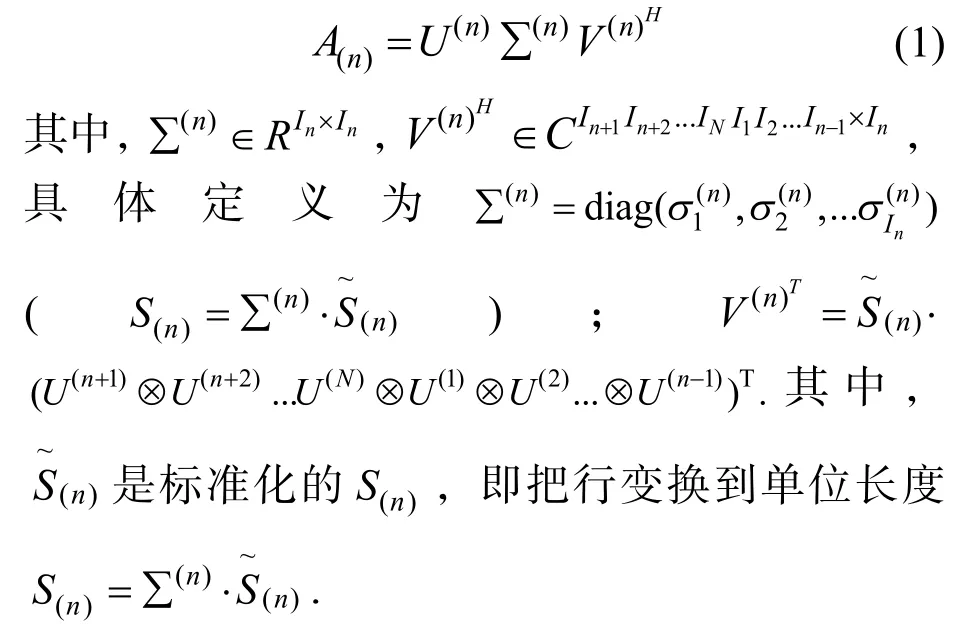
给定一个秩为n的矩阵，最小方误差意义上最逼近它的秩为r的矩阵，是通过SVD分解去掉较小的奇异值得到的，但这种情况并不适用于阶数N＞ 2的张量，去掉较小的奇异值往往不是最好的近似，但结果一般也还可以．为了找到好的近似， Lathauwer，Turney 和Wang[2-5]等提出了不同的张量分解方法．

假设是张量A的近似，那么对A的拟合度用

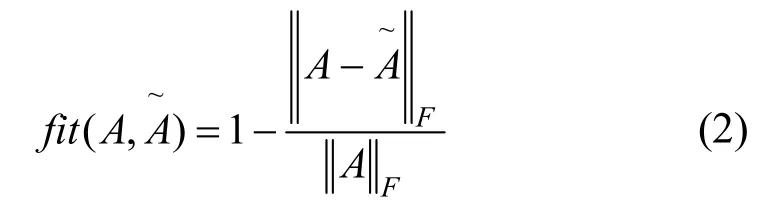
来度量．若该值越接近1，表明拟合的越好．

1.1 Higher-Order Singular Value Decomposition

(HO-SVD)方法

对N阶张量A的分解，HO-SVD的算法过程如下所示．

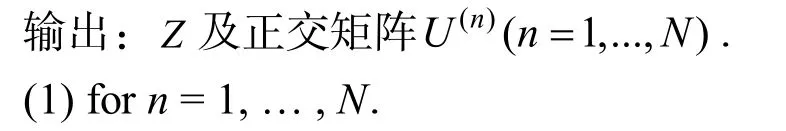
展开A得到计算的前个较大的特征值对应的特征向量，将这些特征向量nJ组成的矩阵赋给()nU．

end for．

从该算法过程，可以看到HO-SVD分解并没有尽力去优化拟合度即没有得出一个秩为的对A较好的近似，因为只是把每阶单独优化，没考虑到各阶的相互作用．

1.2 Higher-Order Orthogonal Iteration方法

给．

HOOI用HO-SVD来初始化矩阵，它从张量整体和其他的矩阵来计算每个矩阵，并尽力优化拟合度计算量较大．

1.3 Slice Projection (SP)方法

SP介于HO-SVD和HOOI之间，它从张量和另一个矩阵来计算每个矩阵，并尽力优化拟合度，计算量小于HOOI．

1.4 Multislice Projection(MP)方法

对4阶张量A的分解，MP算法过程如下所示．

从上面的算法过程我们可以看到MP的基本结构来自于SP，可是MP用了所有的矩阵去计算每一个矩阵，而不是只用一个矩阵，计算量略大于SP，但拟合效果较好．

Turney[3]总结了这 4种方法并做了实验，总体上来说，相比HO-SVD和HOOI需要较大的内存，SP和MP能处理大张量，速度也较好，拟合度最好的是 HOOI,接着是 MP, SP, 最差的是HO-SVD．接下来我们将这4种方法应用到人脸识别的研究中，以分析其对人脸识别的影响．

2 张量分析法对人脸识别的分析

为了验证算法的有效性，在ORL人脸库上进行了实验，见图 1．ORL人脸库[15]是剑桥大学AT&T 实验室在1992-1994年间收集，它包括40个不同的人，每个人有 10幅不同的图像，总共400张，均是 256级的大小为 92×112的灰度图像．该数据库包含了光照、人脸表情(眼睛睁开或闭上，微笑或不微笑)和面部饰物(戴眼镜或者不戴)的轻微变化．

图1 ORL人脸库示例

在ORL人脸库中用10-fold交叉验证方法，即轮流将每个人的9张图片作为训练集，剩下的一张作为测试集，这样进行10次，10次结果的均值作为人脸识别率．

将训练图象按图2组成3阶张量，用D表示(D是一个92×112×360的张量)，接着用HO-SVD, HOOI, SP或MP分解D．D=Z×1U1×2U2×3U3．

图2 张量D表示训练数据

最后运用3D-PCA识别人脸．3D-PCA算法步骤如下所示．

训练过程：

输入：训练人脸数据D．

输出：投影特征矩阵ProjectedImages，投影矩阵U1和U2，样本均值m．

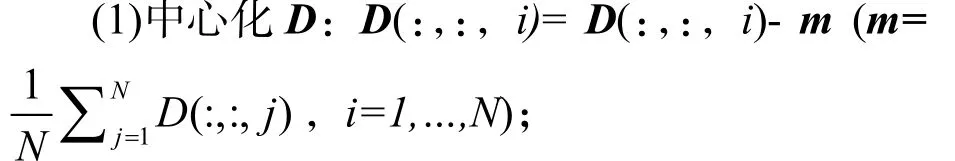
(2)按照之前描述的方法用HO-SVD, HOOI, SP或MP分解张量D得到U1和U2；

测试过程：

输入：未知类别的人脸图像矩阵I和投影特征矩阵ProjectedImages，投影矩阵U1和U2，样本均值m．

输出：该人脸所属类别．

(1)中心化I：I = I-m；

(2)将I向U1和U2投影赋给矩阵T；

(3)计算T和ProjectedImages (:,:,i), (i=1,…,N)的欧式距离，最小距离对应的那张图像就是该未知图像所属的人脸．

这里我们通过识别率随压缩率的变化来比较这4种张量分解方法和PCA方法，压缩率的计算方式如下．

假设训练图象大小为m×n，图象个数为N，张量分解方法中图象压缩为m1×n1，PCA方法中图象压缩为m2．则张量分解方法压缩率r1= (N×n1×n2)/(N×m1×n1+m×n1＋m1×n)，PCA方法压缩率r2= (N×n1×n2)/(N×m2+m×n×n2)．

如图3所示，从实验结果中我们可以看到，4种张量分解方法明显优于PCA方法，而这4种张量方法从图中看不出差别．

图3 ORL数据库上各种方法的比较

我们用表格的形式来仔细比较这4种张量分解方法的结果，如表1所示，可以看到4种张量分解方法在相同的压缩率下的识别率基本相同，即使有不同也差别不大，难以看出明显规律．文献[3]中指出拟合度最好的是HOOI，接着是MP，SP，最差的是HO-SVD．这样效果最好的应该是HOOI，接着是MP，SP，最差的是HO-SVD，这跟表1的实验结果并不相符．

文献[3]中用来做实验的数据最小是250×250×250，在张量较小的情况下HO-SVD的拟合度也不错，因此效果不是很明显，而我们用到的人脸数据是92×112×360，这是与实验结果不相符的原因之一，另外影响人脸识别的因素较多，不一定拟合度越高，识别率越高．考虑到用来做实验的人脸图象较小，所对应的张量都不是大张量，而HO-SVD比较简单，而且文献[2]指出尽管HO-SVD计算过程中并不验证拟合度，但它分解出来的拟合度一般都还不错．于是，基于张量框架的人脸识别实验涉及的张量分解方法可以采用HO-SVD方法．

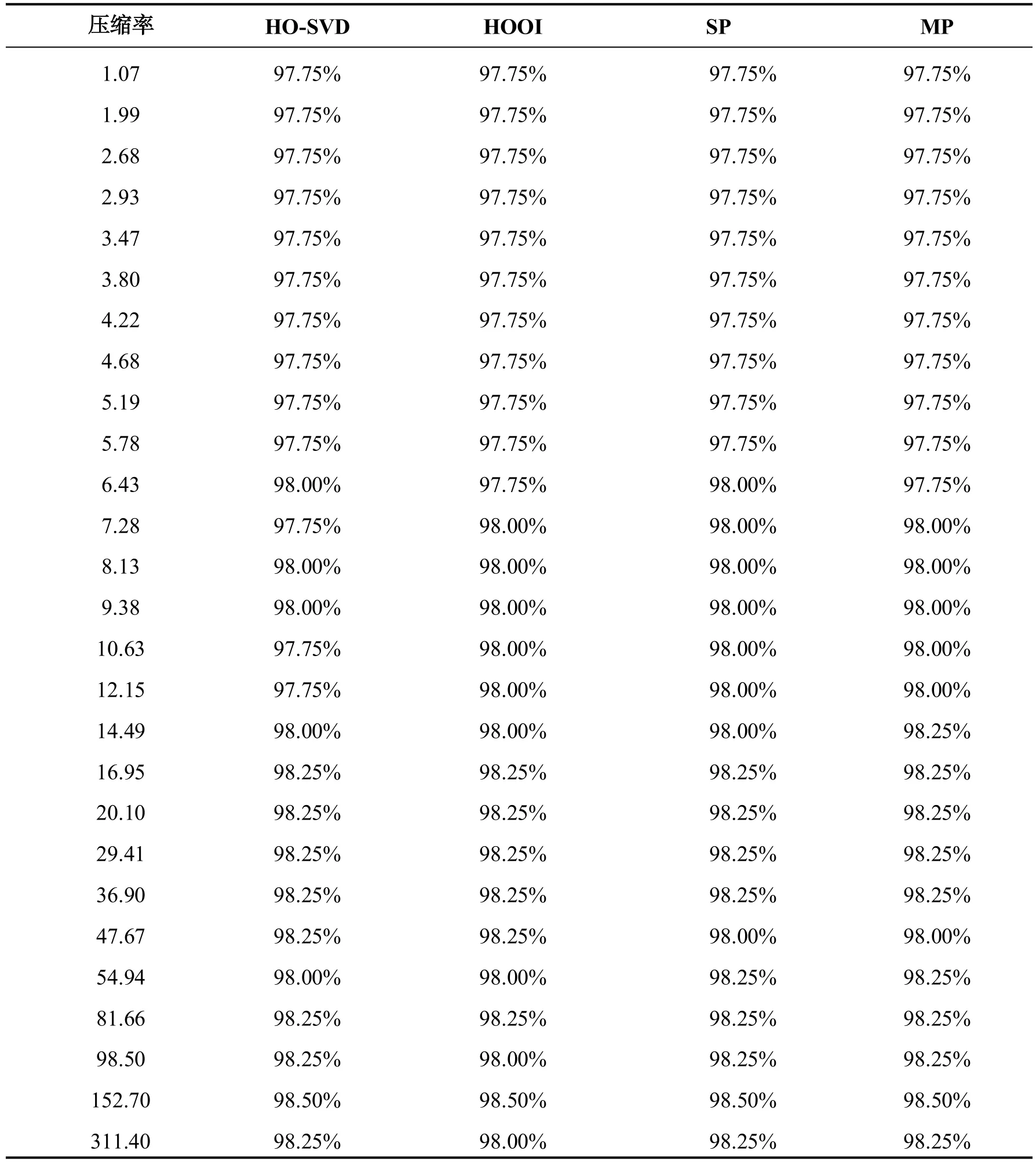
表1 4种张量方法随压缩率变化的识别率

3 小结

本文分析了几种张量分解方法，并在 ORL人脸数据库上分析了4种经典的张量分解方法和PCA方法对人脸识别研究的影响．结果表明，相比PCA方法，张量方法在压缩率大的情况下性能有着显著的提高．另外，对比不同的张量分解方法，我们发现，尽管理论上分析HOOI拟和度最好，但用到实际人脸数据上这4种方法并没有多大差别，这主要是由于人脸图象较小，不涉及大张量．鉴于HO-SVD方法比较简单，对于人脸识别涉及的小张量，分解出来的拟合度都能满足需求，因此可选用HO-SVD方法用于人脸识别研究．

参考文献：

[1]Tucker L R. Some mathematical notes on three mode factor analysis[J]. Psychometrika, 1966. 31(3): 279–311.

[2] Lathauwer L D, Moor B E, Vandewalle J. A multilinear singular value decomposition[J]. SIAM Journal on Matrix Analysis and Applications, 2000, 21(4): 1253-1278.

[3]Turney P D. Empirical evaluation of four tensor decomposition algorithms[Z]. Departmental Technical Report, 2007.

[4]Lathauwer L D, Moor B E, Vandewalle J. On the best rank-1 and rank-(R1, R2, …, RN) approximation of higher-order tensors[J]. SIAM Journal on Matrix Analysis and Applications, 2000, 21(4): 1324–1342.

[5]Wang H, Ahuja N. Rank-R approximation of tensors: Using image-as-matrix representation[A]//Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition[C]. San Diego: Canifornia, 2005.

[6]Vasilescu M A O, Terzopoulos D. Multilinear projection for appearance-based recognition in the tensor framework [A]// Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition[C]. USA: Minneapois, 2007.

[7] Vasilescu M A O. Multilinear projection for face recognition via canonical decomposition[A]//Proceedings 2011 IEEE International Conference on Automatic Face & Gesture Recognition[C]. USA: Santa Barbara, 2011.

[8] Hao N, Kilmer M E, Braman K,et al. Facial recognition using Tensor-Tensor Decompositions[J]. Society for Industrial and Applied Mathematics. 2013, 6(1): 437-463.

[9]Zhang F, Qi L, Chen E Q. Face Recognition via Multi linear Principal Component Analysis and Two-Dimensional Extreme Learning Machine[J]. Journal of Computational and Theoretical Nanoscience, 2015, 12(7): 1138-1146.

[10]Zhang F, Wang X, Sun K. A report on multilinear PCA plus GTDA to deal with Face Image [J]. Cybernetics and Information Technologies, 2016, 16(1): 146-157.

[11]Lita L, Pelican E. A low-rank tensor-based algorithm for face recognition[J]. Applied Mathematical Modelling, 2014, 39(3-4): 1266-1274.

[12]Cao X, Wei X, Han Y,et al. Robust face clustering via tensor decomposition[J]. IEEE Transactions on Cybernetics, 2015, 45(11): 2546-2557.

[13]周春光, 孙明芳, 王甦菁, 等. 基于稀疏张量的人脸图像特征提取[J]. 吉林大学学报, 2012, 42(6): 1521-1526.

[14]胡小平. 基于张量的多线性思想对主成份分析方法的改进[J].安庆师范学院学报, 2012,18(4): 38-43.

[15]Chen W S, Zhao Y, Pan B B,et al. Supervised kernel nonnegative matrix factorization for face recognition[J]. Neurocomputing, 2016, 205: 165-181.

(责任编校：陈健琼)

Comparison and Analyses of Four Tensor Decomposition Methods on Face Recognition

HU Xiao-ping
(School of Computer & Information, Anqing Normal University, Anqing, Anhui 246133, China)

The tensor decomposition is the high-order generalization of principal component analysis (PCA), and nowadays multiple tensor decomposition methods coexist. These methods have their own advantages and disadvantages, and none can satisfy all the characters of PCA. The dissertation compares and analyzes four tensor decomposition methods on ORL database. The results show that these methods perform close on face recognition, for face data are not big tensors and the small differences of the fit do not affect recognition rate. So, the Higher-Order Singular Value Decomposition (HO-SVD) can be used to investigate face recognition due to its simple processing and equivalent results.

face recognition; tensor decomposition; principal component analysis; tensor

TP391.4

A

10.3969/j.issn.1672-7304.2017.01.14

1672–7304(2017)01–0067–06

2016-09-02

安庆师范大学青年基金项目(KJ201407)

胡小平(1984-)，女，安徽桐城人，讲师，硕士，主要从事图像识别研究．E-mail: lisa_0102@126.com