一种基于降维思想的K均值聚类方法

徐 勇，陈 亮(安徽财经大学 管理科学与工程学院，安徽 蚌埠 233000)

一种基于降维思想的K均值聚类方法

徐 勇，陈 亮
(安徽财经大学 管理科学与工程学院，安徽 蚌埠 233000)

维数灾难是数据挖掘过程中的重要问题．为解决K均值聚类过程中的维数灾难问题，本文以欧式距离作为距离的计算方式，采用主成分(PCA)方法对数据源进行降维，实验获得在不同数据规模、特征下的K均值方法的聚类时间．设置对照组对时间、差异性、迭代次数三个方面进行比较．通过实验总结出，数据源的大小与维数共同影响降维聚类的时间效益：数据数量越大，降维聚类的时间收益越大，数据维数越大，降维聚类的时间收益越小；数据源的线性程度影响降维聚类与非降维聚类结果的差异大小：数据线性程度越高，两次聚类结果差异性越小．反之，差异性越大；K均值算法收敛速度很快，两次聚类都能在Sqrt(Row)次数内完成程序的收敛．

聚类算法；降维；K均值；主成分分析

随着无线遥感、GPS技术的发展，给人们带来便捷的生活．人们在享受着位置服务的同时，也面临着位置隐私的泄露问题．位置隐私中的轨迹隐私包含了人们的日常活动信息，通过轨迹隐私可以推测出人们的宗教信仰、出行计划等隐私信息．攻击者可以通过这些信息对用户进行广告的精准投放、诈骗等行为，给用户带来财产上的安全隐患．所以，有必要对用户的轨迹隐私进行保护．轨迹隐私保护常用的方法是位置信息的泛化，通过K均值聚类的方法，对轨迹数据采样并聚类，然后发布模糊的轨迹数据．

K均值算法是一种非监督实时聚类算法[1]，算法的核心思想是根据到中心点的距离，把所有的对象分配到不同的类别当中去．其中，根据问题的不同，距离的计算方式也会不同．对两个被n个数值属性描述的对象i,j，令用曼哈顿距离表示为

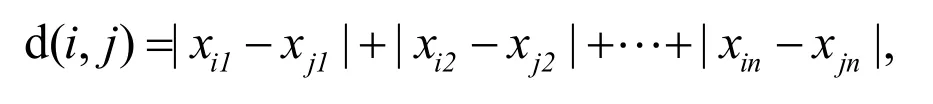
在欧式距离下表示为

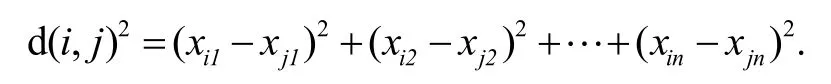
K均值算法的时间复杂度为O(nmkt),其中n是对象数目，m是对象属性数，k是聚类数目，t是迭代次数．对于给定数据集，在用K均值算法进行聚类的时候，要把每个对象的每个属性参与运算．如果属性过多、数据量较大，消耗的时间是难以忍受的．在轨迹隐私保护中，轨迹泛化需要对大量轨迹与大量采样点进行聚类，需要进行多个维度大量数据的矩阵运算，传统的K均值聚类计算时间过长，面临维度灾难问题．

现实事物的属性或者因素之间很多都是存在某种线性或者非线性的关系．在K均值算法中，如果参与运算的属性之间存在某种函数关系，那就可以考虑通过降维方法对数据进行降维，减少参与运算数据的维数，从而达到减少算法运算量，缩短运行时间的目的．

在解决维数灾难问题上，国内外学者提出了很多方法．在提取线性特征方面，主成分分析(PCA)[3]和 Fisher 线性判别分析(FLDA)[4]得到广泛的运用．对于非线性的特征提取，核方法[5]是运用最广泛的方法之一，核主成分分析(KPCA)[6]、核 Fisher 线性判别分析(KFLDA)[7]等核方法已经获得了较广泛的使用．特别地，以 ISOMAP[8]、LLE[9]等为代表的方法，针对非线性、数据流形的特征提取有着较好的效果．

国内外有很多运用降维思想解决实际问题的研究，针对数据不同的特点，也会采用不同的降维方法．例如，主成分分析算法对基因表达数据进行聚类[10]、把加入主成分分析的K均值聚类法运用于洪水预报[11]等是基于数据之间存在线性关系；KPCA与SVM相结合的分类[12]、基于核主成分分析与小波变换的高质量微博提取[13]等是基于数据之间存在非线性关系．

对于每种降维方式，都有其的适用场景与不足．如PCA、KPCA具有良好的去除噪声的功能，但是PCA降维时间复杂度较高，当维数较大时，需要大量的时间降维．FLDA对特征抽取效果非常好，但是在高维、小样本情况下如何抽取Fisher最优鉴别特征仍是个难题．

把降维思想与其他方法结合是解决问题的一个思路．当前，已经有很多研究把降维和K均值聚类结合解决实际问题．例如，文献[11，14-15]都是将 PCA与 K均值结合运用到各个应用中去．目前这些研究是基于降维思想的K均值聚类方法在某一方面的运用，对降维带来时间收益没有一个定量的认识，对降维效果的影响因素比较含糊，没有一般性地讨论降维K均值聚类的步骤以及降维可能带来的问题．

为解决类似轨迹隐私保护中的维数灾难问题，本文以基于主成分分析方法的K均值聚类为例，讨论了降维思想在K均值聚类的运用以及可能出现的问题．为了方便说明，文中的数据集存在完全或者近似线性关系，采用欧式距离作为距离计算的标准．相对于其他文献工作，本文的不同之处在于，更加一般性地讨论运用降维方法进行K均值聚类的方法、步骤，并通过实验讨论降维聚类的时间节省、差异性、迭代次数3个层次的各种影响因素．

1 PCA相关概念

1.1 PCA处理步骤

(1)将原始数据按照行的方式组成n行m列的矩阵X；

(2)求X每列的平均值，然后让该列的每个数减去平均值，得到矩阵D；

(4)求出协方差矩阵的特征值及其对应的特征向量；

(5)将特征向量按照对应的特征值大小进行排列，取前p个特征向量组成矩阵P；

Y是降维后的数据，该方法把冗余、无关的属性去掉，得到最重要的属性的组成矩阵排列，是原有数据信息很好的保留．

1.2 PCA的实质

由上面的描述可以看出，主成分分析法的实质就是原矩阵在新的标准正交基上的变换．存在线性相关的几个维度会导致1个或者多个对应的特征值为0或者相对较小，这些维度的数据经过标准正交变换之后，基本都落在一个常数c上，这样这个维度对全局的影响就很小．这时候用0向量替代方差贡献率比较小的特征向量，消去这些维度，达到降维的目的，同时平滑了噪声．

变化过程中，原矩阵会和变换后的矩阵有很大的差异，例如 A(1,3)，B(2,6)两点组成的矩阵经过降维之后的矩阵为与原始数据集相比存在如此大的差异的情况下，降维聚类的结果是否贴近实际的结果还需证明．

1.3 PCA运用到K均值合理性

当K均值采用欧式距离作为距离的计算标准时，特征值比较小的维度上的数据基本落在了常数c上，这样数据对欧式距离的贡献很小，舍去以后几乎不会影响类别的划分，同时也降低了异常点对聚类结果的影响，让数据变得更加平滑，这些是 PCA运用到 K均值聚类的必要条件之一．只要证明经过标准正交变换之后，对象与对象之间的距离不变，那么主成分分析法就可以运用到K均值算法中去．下面给出数学证明．

设空间中的两点A、B与坐标原点O之间组成的向量为X，Y．则A、B两点之间的距离的平方为设新的正交基为C，则A、B两点在新的正交基下与原点之间的组成的向量为XC、YC．根据矩阵运算的结合律可知，A、B两点在新的正交基下的距离的平方为

通过上述证明可以得出，经过标准正交变换之后，对象与对象之间的距离不变．

2 算法设计

本部分主要对基于PCA的K均值方法的算法进行描述，给出相应的算法流程，同时对程序的算法复杂度进行分析，并根据算法复杂度对降维成本与减少的计算复杂度的关联进行讨论．

2.1 算法描述

2.1.1 Main函数的算法描述

在一次试验中，首先按照要求产生数据．为了与非降维聚类比较，同一数据集聚类2次，并记录下聚类结果和聚类时间，最后比较这2个指标的差异．

首先，按照行数、列数、线性程度3个参数产生相应的数据，并将产生的数据存放到txt文档中，用于反复实验．然后将产生的数据读入内存，并用矩阵Source对象存放，之后记下此时毫秒数为T0．直接聚类，聚类结果出来时，再次记下此时毫秒数为T1，同时把聚类结果1临时存放在内存中，用List集合保存起来．然后对Source进行降维，得到中间结果的矩阵对象 Target，记下此时毫秒数为T2，再对矩阵Target进行聚类，得到降维聚类的结果2，同时记下此时的毫秒数T3．第1次聚类时间为T前=T1-T0，第2次聚类时间T后=T3-T1，降维的时间为T降=T2-T1，降维后聚类的时间为T聚=T3-T2．比较T前与T后的大小就可以得出哪种方式的聚类时间少，分析T降与T后可以获得原因；分析结果1与结果2每一类中相同的对象数目，可以得到两次聚类结果的差异．

2.1.2 数据产生的算法描述

实验数据前 10列的数值由随机函数随机生成，数据的生成公式为 source[i][j]=random. nextInt(maxSize)，10列以后的数据按照下面的公式 生成： source[i][j]=(1+r)*source[i][j%10]±r* source [i][j%10]．其中，source [i][j]是矩阵第i行第j列的值，maxSize是随机函数产生的最大的数，r为0-1之间的1个随机的小数．r*source [i][j%10]用于生成随机扰动项，r一般很小，定义为随机扰动因子，可以作为衡量数据之间的线性程度．r越小，表示线性程度越强．该公式生成的数是矩阵中第i行第j%10列的数乘以1个随机倍数，再加上1个随机扰动项．如表1中的5*20的数据，第11列的每行数据是第1列的每行数据的1.1倍加上1个随机扰动项，第12列每行的数据是第2列每行数据的1.3倍加上1个随机扰动项．随机扰动项是为了模拟现实中可能出现非完全线性的数据．这种非线性将很大程度影响降维后的聚类结果．这样就保证了第11列以后的数据和前10列具有近似线性关系．

表1 数据集示例

2.1.3 PCA方法的算法描述

PCA实现的算法，可以参考1.1节中的步骤进行．在算出特征值以后，对特征值进行累加，然后对这些特征值进行排序．根据数据特点，选取不同的标准对维度进行保留，获得理想的效果．维度选择的标准影响降维后的维数，进而影响数据之间距离信息的损失．数据特征不同的特点决定了维度选择的标准并非单一．

程序中根据所产生的数据集的特点，采用以下2种标准对维度进行选择．

一种以方差贡献率大小为选取标准．定义方差贡献率阀值为Q，当方差贡献率rate≥Q时，保留该维，当rate＜Q时，舍去该维，其中Q小于总维数的倒数．通过控制方差贡献率的阀值，可以控制降维后的维数．但是这种方式在近似线性的情况下，容易出现降维过度的情况，即大部分的维度被舍去，造成两次聚类结果差异较大．

一种是直接指定降维后的维数．例如原来的数据是100维，人工指定降维到60维．这种方式是为了弥补上一种方式的降维过度的情况．但是这种方式依赖于人的经验，当数据量比较大的时候，很难把握合适的降维维数．

当数据集存在完全线性、完全非线性关系时，以方差贡献率大小为选取标准可取得很好的效果．当存在数据集存在近似线性关系时，直接指定降维后的维数的方式会取得很好的效果．当然，没有绝对标准，维度保留的标准要依据需求选取．

2.2 降维成本与时间收益

降维聚类的时间包含降维和聚类2个部分，要了解能否通过降维减少聚类时间带来时间上的收益，需要分析PCA的时间复杂与K均值时间复杂度之间的关系．

2.2.1 算法复杂度分析

根据1.1节的步骤，求步骤(2)的时间复杂度为O(nm)，求协方差矩阵C需要进行矩阵相乘，所以步骤(3)的时间复杂度为O(nm2)．分析JAMA源码可知，步骤(4)的时间复杂度为O(m2)，步骤(5)的时间复杂度为O(mlogm)，步骤(6)的时间复杂度为O(nmk)．所以PCA降维总的时间复杂度为O(nm2)，降维的时间与行数正比，与列数的平方成正比．

降维前，K均值算法的时间复杂度为O(nmkt) (k是聚类数目，t是迭代次数)，降维后的时间复杂度为O(npkt)(p为降维后的维数)．所以降维聚类总的时间复杂度为O(npkt) +O(nm2)，与降维前的O(nmkt)相比，两者都在1个数量级上．

2.2.2 时间收益分析

假设降维前的聚类与降维后的聚类迭代次数相同，保持维数m不变，降维后的维数为p，同时满足m=bp(b＞1)．那么降维前聚类的时间复杂度可以简化为O(nkt)，降维后的聚类时间复杂度可以简化为(C/b)O(n(m+kt))，其中C为两种聚类方法时间复杂度的系数之比．因为m为常数，当数据量不断增大时，k与t也会变大，T前/T后的值也会增大，当k与t的乘积远大于m2时，T前/T后的值会趋近于定数F，其中F=Cb．可以通过实验求得T前/T后的值F，进而求得常数C．通过这个性质来预测降维后的时间缩减，即指定维数后，便可估算出降维聚类的运行时间为原来的T后/T前倍．事实上降维前的聚类与降维后的聚类迭代次数不一致，所以T前/T后趋近的值不会这么准确．所以，在维数不变的情况下，数量越大，降维聚类越能减少聚类总时间．

假设降维前的聚类与降维后的聚类迭代次数相同，保持行数n不变, 那么降维前聚类的时间复杂度可以简化为O(m)，降维后的聚类时间复杂度可以简化为O(m2)．所以，当数据行数不变，维数增大时，非降维组聚类的时间消耗成线性增长，降维聚类的时间消耗为2次函数形式增长，会更加消耗降维总时间，具体增长形式会受到迭代次数的影响．

降维聚类会导致迭代次数的变化，当数据集完全线性的时，保留全部非0特征值时，降维前后对象之间的距离不变，两次聚类的迭代次数一致；当数据近似线性时，不保留全部特征值，会出现距离信息损失，对象之间距离会发生变化，两次聚类的迭代次数会不一致．因为降维并不会一定减少迭代次数，而且K均值算法具有收敛速度快的特点，迭代次数很少，所以迭代次数并不是影响程序执行时间的主要因素．

综上所述，降维聚类能否节省时间主要受到数据行数与列数共同的影响．降维聚类总的时间复杂度为O(npkt)+O(nm2)，不进行降维的聚类的时间复杂度为O(nmkt)，当数据量很大时，聚类数目很多、和迭代次数很大，可考虑用降维聚类．

3 实验研究

为了检验基于降维方法的算法优劣，以及不同数据特征的数据集对降维聚类结果的影响，下面的所有数据都是通过计算机程序所造．所以本文只讨论降维算法的实现和评价，降维聚类的实际应用不在本文讨论内容之内．程序的硬件环境为 AMD A6-3420M APU with Radeom(tm) HD Graphics 1.5GHz，运行环境为jdk1.8．

为了衡量降维效果，考察随机扰动因子R、矩阵行数(条目数)ROW、矩阵列数(维数)3个变量，观察其他条件不变时，某个条件变动对程序的执行时间和聚类差异比率的影响．设降维前的列数为COL前，降维后列数为COL后，降维前程序执行时间为T前，降维后程序执行总时间为T后，其中降维所用时间为T降，降维后聚类的时间T聚，程序执行减少的时间为ΔT，满足T后=T降+T聚，ΔT=T降-T后．实验中，时间的单位为毫秒(ms)．定义差异率DR为2次聚类的结果中存在差异的数目/总数目*100%．

最终的聚类数目k采用经验值并且每隔个数据选取一个初始中心点．

3.1 差异性影响因素实验

本部分主要分别考察降维后的维数(COL后)、随机扰动因子(R)对降维聚类与直接聚类结果的差异．第1部分研究COL后对差异性的影响，第2部分研究R对差异性的影响．

(1)选取数据集为10 000行，100列，聚成100个类．控制随机扰动因子为0.01，这样造出来的数据近似线性，所以采用指定降维维数COL后．当COL后在80、60、40、20变动时，结果见表2．

表2 COL后变动程序执行的结果

由表2可知指定降维后的维度越小，程序执行的时间显著减少，同时伴随着差异率的上升．程序减少的时间主要来源于T聚相对于T前的减少．数据集的维度下降了，等同于数据量减少了．

实验中，每减少 20维，降维时间大约减少100毫秒．在2.2.1小节的分析中，PCA降维的过程中只有步骤(6)是和降维后维数相关，时间复杂度为O(mnk),与降维后的维数是线性关系，其他步骤都和m、n有关系．本次试验中，只是变化了降维后的维，k,m,n并没有变化，所以，降维的时间会呈现线性减少．

程序确实减少了聚类时间，同时，两次聚类结果也存在一定的差异．造成这个原因的有2个，一是降维会造成信息丢失；二是程序在矩阵运算过程中，四舍五入的情况会导致精度的损失．

(2)选取数据集同样为10 000行100列，聚成100个类．指定降维维数COL后为60．让随机扰动因子按照0.1、0.05、0.01、0.005变动，生成4个数据集，程序执行的结果见表2.

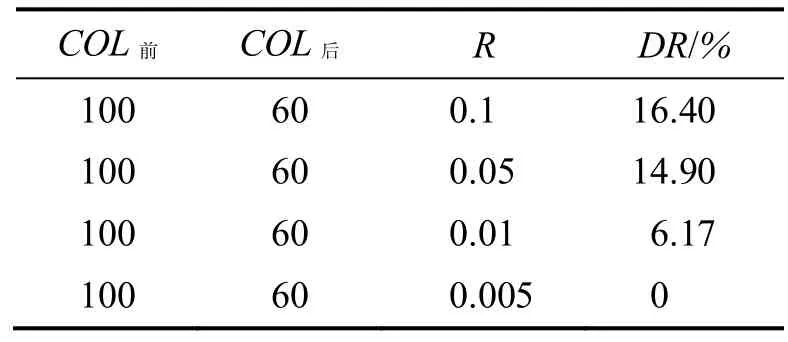
表3 随机扰动因子变动程序执行的结果

随机扰动因子越小，差异比率越小．也就是说，当数据之间线性关系越强时，降维聚类的结果越接近直接聚类的结果．

从上面的两个实验结果可以总结出，随机扰动因子R与选取的降维后维数COL后对降维差异率DR有很大影响．当数据集的R一定的情况下，如果要减小这种差异率，可以增大COL后．

3.2 时间节省因素实验

本部分主要分别考察数据集行数、数据集列数对降维聚类结果的影响．为了演示效果，控制数据集为完全线性，根据方差贡献率获得最终降维维数．第1部分研究数据行数对节省实验的影响，第2部分研究列数对时间节省的影响．

(1)把数据保持100维，随机扰动因子为0，控制为完全线性，差异率控制为 0，最终降维为10维，条目按100，1 000，10 000，20 000，40 000变化时，程序的节省时间见表4．从表4可知，当数据量增大时，受迭代次数影响，无论是T前还是T聚，并不是随着条目数的增长而线性增长，聚类时间增长的倍数要大于条目数增长的倍数，而且聚类时间增速非常快．

原数据集为100维，最终降维为10维，根据2.2.2小节的结论，T前/T后的值会不断增大，并趋近与1个定值．观察表中T前/T后值的变化，前面4组值在不断增大，最后4组在4.84～5.96波动，验证了此理论．COL后/COL前的值为10，根据可以根据这几组实验估算出C的值为4.84～5.96之间．即在数据量比较大的情况下，维度每降低 1倍，聚类时间减少0.484～0.596倍．这是实验测的C值，真实的 C值会有所差距，因为在试验中，每组的数据都不一样，迭代次数也不一样，并且在执行过程中还要受到CPU状态、运行期优化等影响．

(2)把数据保持10 000行，随机扰动因子为0，控制为完全线性，差异率控制为 0，最终降维为10维，列数按照50，100，200，400，800变化时，程序的节省时间如表5所示．

表4 数据量变动程序的执行结果

表5 列数变动时程序执行的结果

从表5可知，在行数不变的情况下，T前随着列数的增长而线性增长．T后最初小于T前，但是当列数增长至800时，T后远远大于T前．ΔT/T前逐渐减小直至为负可知，在列数不断增长时，程序节省时间效果逐渐减小．因为数据的条目没有变化，所以T聚几乎没有变化．T降增长速度也不断增大，通过少量计算，如表6，得出与COL前的平方近似成线性关系．虽然COL2前/T降的大小没有稳定在 4，但是可以看出，降维时间和列数平方之间的关系为相同数量级上，与也符合前面分析的PCA的时间复杂度为O(nm2)．PCA降维过程中，第6步的时间复杂度为O(nm2)，省略了其他5步的时间复杂度，所以，COL2前/T降没有稳定在4波动．ΔT先增长，后下降为负，原因是降维花的时间随着列数的增加而变得很长，降维的时间成为程序执行最主要的消耗时间．

表6 COL2前与T降的变化关系

从上面2个实验可以总结出，列数不变的情况下，数据量越大，降维节省的时间效果越好．这是因为一方面降维的时间增加的比较缓慢；另一方面，降维会导致参与运算的数据的减少，从而聚类运算时间极大减少．在行数不变的情况下，列数的增加会降低降维聚类带来的时间红利．这是因为随着列数的增长，降维的时间将成为主要的运算时间．当列数达到一定的数目之后，降维聚类将耗费更多的时间．T降与T聚到底哪个成为运算的主要时间，取决于数据行数和数据列数的相对大小．

3.3 迭代次数实验

本部分讨论数据量的大小、数据非线性程度对两种聚类方式的迭代次数的影响．第1部分研究数据量的上升迭代次数的变化．第2、第3部分为对照组，研究非线性程度对两种降维方式迭代次数的影响．

(1)把数据保持100列，随机扰动因子为0，控制为完全线性，差异率控制为 0，最终降维为10维，行数按100，1 000，5 000，10 000，20 000变化时，迭代次数见表7．

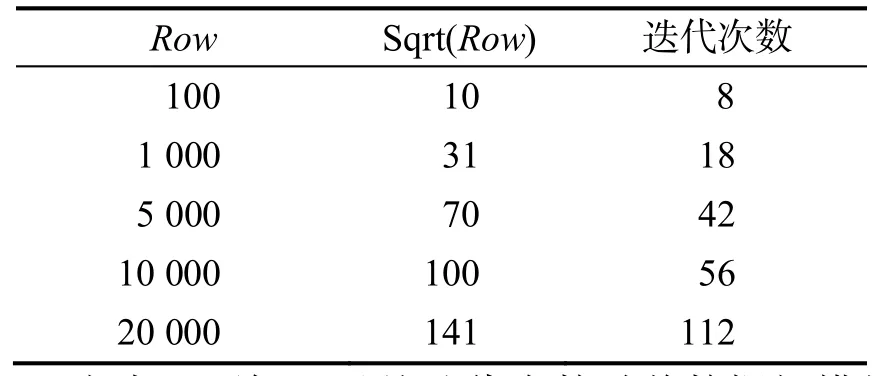
表7 迭代次数

由表7可知，虽然迭代次数随着数据规模的增长而增长，但是却没有想象中的那么迅速，基本能在Sqrt(Row)次数完成程序收敛．这也体现了K均值算法良好的收敛性．

(2)把数据保持100列，随机扰动因子为0，控制为完全线性，差异率控制为0，行数按照100, 500, 1 000, 2 000, 10 000变化时，2次聚类的迭代次数见表8．

表8 完全线性时迭代次数

由表8可以看出，在数据完全线性时，2次迭代次数一样．这是因为完全线性导致只有 10个非0特征值，导致前10个特征值已经包含了对象与对象之间所有的距离信息，所以迭代次不会改变，只也验证了1.3小节中“变化标准正交基不改变对象之间距离”的理论．

(3)把数据保持100列，随机扰动因子为0.1，控制为近似线性，降维后维度指定为50维，行数按100，1 000，10 000变化时，2次聚类的迭代次数如表9所示：

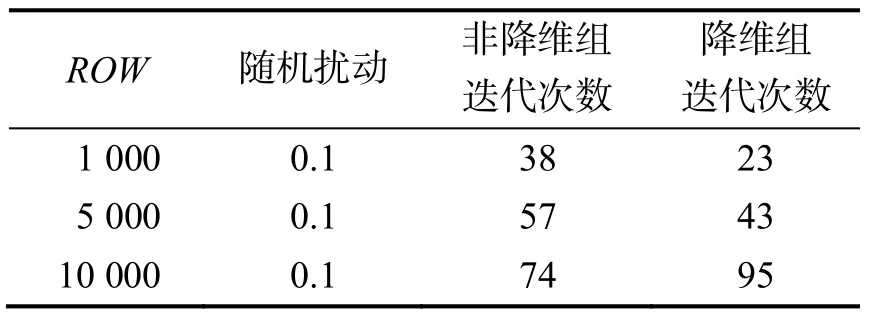
表9 随机扰动因子为0.1时迭代次数

由表9可以看出，在数据近似线性时，两次迭代次数不一致．这是因为近似线性导致只非 0特征值大50个，而程序之选取了前50个特征值，导致了对象之间部分距离信息的损失．降维的数据之间的距离发生变化，所以迭代次数也就发生了变化．

从实验可以得出，K均值算法的收敛速度优良，程序的执行时间与迭代次数之间关系较小．在完全线性时，在充分保留所有非0特征值的情况下，降维不影响迭代次数．在近似线性情况下，保留大部分的维度，由于距离信息的损失，会导致2次迭代次数不一致．

4 小结

K均值算法中使用降维方法与不使用降维方法可以从时间节省、差异性、迭代次数3个方面比较．数据数量越大，降维聚类的时间收益越大，数据维数越大，降维聚类时间收益越小；数据源的线性程度影响降维聚类与非降维聚类结果的差异大小：数据线性程度越高，2次聚类结果差异性越小．反之，差异性越大．K均值算法收敛速度很快，2次聚类都以相对于数据量极小的次数完成收敛．

在定义降维前后2次聚类结果的不同的时候，措辞是“差异率”而不是“错误率”或者“差错率”．因为这种降维带来的差异并不能说它是不好，经过PCA降维处理后，会平滑原数据中的噪声，减少因为噪声数据对聚类结果的影响．每种方法都有它的限制，不会对所有问题都适应，降维聚类效果的好坏应该由实践来检验．关于降维聚类还有很多问题需要去研究，例如如何降低PCA的时间复杂度；当行数与列数形成什么关系时适合降维聚类．文中的数据为人工所造，不能准确反映真实情况，采用飓风轨迹数据进行深入的测试验证和研究．

参考文献：

[1]Macqueen J. Some methods for classification and analysis of multivariate observations[C]// Proc. of, Berkeley Symposium on Mathematical Statistics and Probability. 1967: 281-297.

[2]范明, 孟小峰. 数据挖掘概念与技术[M]. 北京: 机械工业出社, 2012: 48.

[3]Turk M, Pentland A. Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience, 1991, 3(1): 71-86.

[4]Belhymeur P N, Hespanha J P, Kriegman D J. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1997, 19(7): 711-720.

[5]Shawe-Taylor J, Cristianini N. Kernel methods for pattern analysis[J]. Journal of the American Statistical Association, 2004, 101(476): 1730-1730.

[6]Mika S, Rätsch G, Weston J,et al.Fisher discriminant analysis with kernels[C]// Proceedings of the 1999 IEEE Signal Processing Society Workshop. Madison, WI: IEEE, 1999: 41-48. [7]Schölkopf B, Smola A, Müller K. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319.

[8]Tenenbaum J B, De S V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319-2323.

[9]Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326.

[10]Yeung K Y, Ruzzo W L. Principal component analysis for clustering gene expression data[J]. Bioinformatics, 2001, 17(9): 763-774.

[11]师黎, 杨振兴, 王治忠, 等. 基于PCA和改进K均值算法的动作电位分类[J]. 计算机工程, 2011, 37(16): 182-184.

[12]浦路平, 赵鹏大, 胡光道, 等. 基于PCA和K-均值聚类的有监督分裂层次聚类方法[J]. 计算机应用研究, 2008, 25(5): 1412-1414.

[13]刘可新, 包为民, 阙家骏, 等. 基于主成分分析的K均值聚类法在洪水预报中的应用[J]. 武汉大学学报: 工学版, 2015, 48(4): 447-450.

[14]Kallas M, Francis C, Kanaan L,et al. Multi-class SVM classification combined with kernel PCA feature extraction of ECG signals[C]//International Conference on Telecommunications. IEEE, 2012: 1-5.

[15]彭敏, 傅慧, 黄济民, 等. 基于核主成分分析与小波变换的高质量微博提取[J]. 计算机工程,2016, 42(1): 180-186.

[16]傅荣林. 主成分综合评价模型的探讨[J]. 系统工程理论与实践, 2001, 21(11): 68-74.

(责任编校：蒋冬初)

A K-means Clustering Method Based on Dimension Reduction

XU Yong,CHEN Liang
(School of management science and Engineering, Anhui University of Finance and Economics, Bengbu, Anhui 233000, China)

The curse of dimensionality is an important problem in the process of data mining. In order to solve the dimension disaster problem in K means clustering process, this paper uses the Euclidean distance as the way of the distance calculation, employing the principal component method (PCA) of the data source to reduce dimensionality, to acquire clustering time of the K means method in different scales and the characteristics of data by the experiment. And compare both the time and difference with the control group. It is concluded from the experiments that the size and the dimension of the data source combined effect of time benefit of dimension reduction in clustering: the greater the number of data dimensionality reduction is, the bigger the clustering time income is. The greater the data dimension is, the smaller the dimension reduction clustering time income is. The difference degree of linear data source to reduce the influence on difference comparison between clustering by reducing dimension and the another: the higher the linearity degree of data is, the smaller is the two clustering results difference is. On the contrary, the difference is greater. K means algorithm convergence rate is very fast, two clusters can complete convergence with respect to the number of data.

clustering algorithm; dimensionality reduction; K means; PCA

N32

A

10.3969/j.issn.1672-7304.2017.01.12

1672–7304(2017)01–0054–08

2016-02-10

国家社会科学基金项目(15BTQ043)；安徽省自然科学基金项目(1408085MF127)；安徽省高校省级优秀青年人才基金重点项目(2013SQRL031ZD)；教育部人文社会科学研究规划基金项目(12YJA630136)

徐勇(1978-)，男，安徽泾县人，教授，博士，主要从事社会计算、信息安全、数据挖掘研究．Email：uxyong@sina.com