驯鹿足底非规则特征形貌数学模型构建及验证

张 锐，乔 钰，吉巧丽，李建桥



驯鹿足底非规则特征形貌数学模型构建及验证

张 锐，乔 钰，吉巧丽，李建桥

（吉林大学工程仿生教育部重点实验室，长春 130022）

为攻克常规防滑轮胎在冰面上通过性低的难题，以驯鹿足为仿生原型，对驯鹿足底特征形貌进行分析。该文通过逆向工程技术，将驯鹿足单个足底划分为内、外侧边缘曲线、脊线凹槽面和足跟凸冠面4个典型部位。运用1stOp软件和MATLAB软件对特征部位拟合并构建数学模型，利用X射线能谱仪对驯鹿足底特征部位进行元素分析。内、外侧边缘曲线方程的决定系数R分别为0.994、0.992；脊线凹槽面和足跟凸冠面曲面方程的R分别为0.96、0.98。通过模型验证发现，模型拟合值与实际值的相对误差均值在5%以下，实现了驯鹿足底特征形貌从生物模型到数学模型的转化。能谱分析结果表明驯鹿足底除含有大量的碳、氧及氮元素外，硫、硅、铁、铝、钙5种元素含量较高，并且不同部位的元素存在差别。该研究可为工程仿生技术应用于冰路面行驶车辆胎面设计提供新的研究方向和参考依据。

仿生；模型；计算机仿真；逆向工程；驯鹿足底特征

0 引 言

结冰是影响交通运输安全的不利气象条件中最恶劣的条件之一，解决结冰路面汽车防滑问题一直是人们的迫切需求[1]。研究表明，轮胎花纹是影响冬季防滑轮胎防滑性能的重要因素[2-3]，花纹的设计、走向、深度可以直接影响轮胎的诸多性能[4-6]。因此，设计一种具有特殊轮胎花纹结构且在冰路面上拥有高效防滑性能的冬季轮胎具有广阔的应用前景。国外研究人员创造各种试验条件研究橡胶轮胎与冰面的摩擦机理[7-12]。在国内，彭旭东 等[13-19]研究了橡胶与冰面的摩擦机理，并建立相关数学模型。周利坤等[20-22]由章鱼吸盘受启发，设计出一种具有吸盘式花纹结构的轮胎，仿真结果表明该轮胎具有良好的吸附防滑性能。本文从自然界获取灵感，以冰雪环境动物—驯鹿为生物模本，采用工程仿生学技术，研究驯鹿在冰面上的防滑机理，将有助于解决车辆在冰面上难以行驶的难题。

驯鹿（）是一种典型冰雪动物，在冰路面上具有防滑能力。驯鹿拥有钝的脚趾，其具有锋利边缘的新月形足部可以牢牢控制住硬雪以及坚冰[23]。足底特征形貌是驯鹿在冰路面上具有良好防滑能力的关键因素之一，因此研究其足底形貌并结合仿生学原理设计防滑轮胎[24]，将可能改善轮胎在冰路面上的通过性能。研究表明，驯鹿是一种迁徙动物，其脚枕在冬天收缩增固，露出蹄的边缘，便于驯鹿在冰地面行走，防止滑跤[25]。而在夏天，当苔原柔软湿润的时候，脚枕变成海绵状从而提供额外的摩擦力。因此以驯鹿足为仿生原型，研究一种冰面防滑性能良好、低振动、不破坏路面的仿生胎面具有重要理论意义和潜在应用前景。

逆向工程技术的发展为定量描述动物蹄的结构提供了三维表面测量及数字化模型设计方法[26-28]。本文基于逆向工程技术，获取驯鹿足底曲面三维点云数据，利 1stOpt软件的快速公式拟合方法对边缘曲线进行拟合，利用Matlab软件的数据拟合法对脊线凹槽面和足跟凸冠面进行数学建模。

1 驯鹿足底曲面模型重构

1.1 驯鹿足几何模型获取

选取内蒙古自治区根河市鄂温克族区驯鹿，此处驯鹿属于中国亚种，在中国只有该地区有少量饲养。由于鄂温克族习俗，驯鹿不能轻易杀害，故选取的原型均为正常死亡的驯鹿，年龄在十八岁左右。本文选取驯鹿左后足为仿生原型，将驯鹿足底部的污泥等杂质去除，使得驯鹿足底的曲面特征充分显露，如图1a所示。用三维激光扫描仪对3只左后足进行扫描，由于本文只考虑驯鹿足底的几何特征结构对防滑性能的影响，所以将底部的刚毛部分用胶带缠绕避免对扫描结果产生影响。将经过三维激光扫描得出的3只左后足的三维点云模型导入Geomagic Studio中进行去噪处理；通过封装，把点云模型转化成由三角形组成的曲面模型。利用软件中的网格医生自动诊断功能自动识别驯鹿足模型需要修复的区域，逐个对各个区域进行填补漏洞、去除尖点等一系列修复工作，直至模型完整。最后对整个足模型进行平滑处理，得到光滑平顺的驯鹿足几何模型，其中一个模型如图1b所示。为了研究驯鹿足两侧尖锐边缘切入冰面后其足底部与冰面的接触区域，制作2 cm厚的正方形泥板，将驯鹿足压在泥板上，用来模拟驯鹿蹄边缘切入冰后蹄部与冰面的接触情况并分析驯鹿足底的防滑特征，如图1c所示。

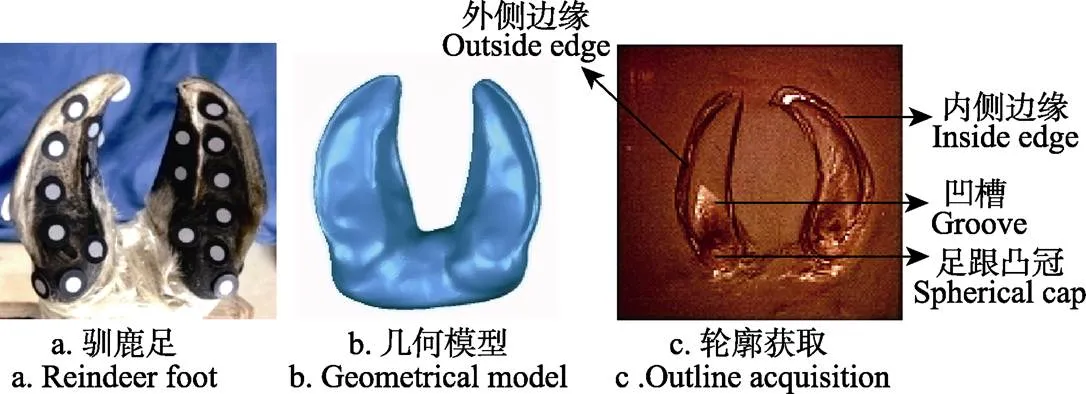
图1 驯鹿足及几何特征

从泥板轮廓上可以清晰地发现驯鹿足底部的内外侧边缘部分全部接触，曲线呈明显的月牙形状，新月形有尖锐边缘的蹄子可抓紧坚冰，并且边缘处相较于中间凸出一部分，这种结构有助于驯鹿蹄更好的切入冰面内。由于选蹄为驯鹿后蹄，观察视频中驯鹿行走以及奔跑时的姿态可以发现驯鹿在运动时后肢向两侧张开，蹄内侧最先与冰面接触，相比于外侧受力更大，因此内外侧驯鹿蹄的边缘部分在运动时施力方式是有区别的，所以分别选取内外侧边缘进行建模，获得内外侧曲线的点云模型。2个凹面的相交线（脊线）在泥板上显露出来，脊线两侧的凹槽面可以帮助驯鹿更稳健得在冰面上行走[25]。由于脊线处是除边缘曲线外与地面接触的第二部分，且对于冰面的施力方式也大致相同，故只选择了外侧蹄部脊线处曲面进行曲面拟合，足跟凸冠面也是如此。最后利用Geomagic Studio中的曲线提取功能提取3个扫描模型的内外侧曲线；利用切割功能获取3个扫描模型的脊线凹槽面与足跟凸冠面，如图2所示。在Geomagic Studio软件中把分割完成的曲线、曲面转化成点云，保存成asc格式文件并转换成TXT格式文件，得到了不同特征部位的三维坐标数据。将3个足部模型同一特征部位的坐标数据进行整合，为数学建模提供数据依据，最终拟合的数学模型带有3个足部的特征。

a. 脊线凹槽面 a. Ridge groove surfaceb. 足跟凸冠面 b. Spherical cap surface

1.2 边缘曲线的点云处理

由于在Geomagic Studio中对内外侧边缘曲线的点云数据是高精度提取，所以需要把曲线的点云数据导入到CATIA的数字化设计（digitized shape editor）模块中进行过滤处理。根据驯鹿蹄足底曲线的形貌特征，选取非均匀过滤，也叫自适应过滤（adaptive filtering）[26]。内侧边缘曲线过滤前数据点为937个，过滤后数据点为36个；外侧边缘曲线过滤前数据点为1024个，过滤后数据点为37个。过滤后点云数据大量减少，但是点云过滤并没有改变曲线的主要形貌特征，过滤前后曲线点云图如图3所示。由于曲面点云数量适中，故没有对曲面点云进行过滤处理。

a. 过滤前外曲线 a. Outside curve before filtratingb. 过滤前内曲线 b. Inside curve before filtrating c. 过滤后外曲线 c. Outside curve after filtratingd. 过滤后内曲线 d. Inside curve after filtrating

2 驯鹿足底数学模型

2.1 边缘曲线数学模型

由于驯鹿足底内外侧边缘曲线是空间曲线，因此需要专业的曲线拟合软件1stOpt[29]对其进行拟合。将内外侧边缘曲线的三维坐标数据导入到1stOpt中，并定义为自变量，为因变量（其中，，为内外侧边缘曲线点云的三维坐标数据，mm），采用麦夸特法（Levenberg- Marquardt）以及快速公式拟合搜索方式对内、外侧边缘曲线进行拟合。考虑到工程应用以及模型的精度要求，只选择1stOpt软件中公式集的上半部分即可，内、外侧边缘曲线拟合方程如式（1）和式（2）所示。

1=27.411-0.747-0.0712-0.817-0.2142（1）

2=28.243-0.974-0.0982-0.168-0.1372（2）

式中为边缘曲线点云在轴方向的数据，为边缘曲线点云在轴方向的数据。,的最高指数均为2次，符合一般的工程应用，方便加工。式（1）和式（2）的均方差（RMSE）分别为0.032、0.020；误差平方和（SSE）为0.037、0.010，均远远小于1；决定系数（R）为0.994和0.992，均接近于1。这表明生物模型被成功转化为数学模型，并且方程精度很高。式（1）和式（2）在系数上存在一定的差别，这可能与驯鹿足底的受力方式有关。拟合图形能够表示驯鹿足底内外侧曲线的基本特征，如图4所示。

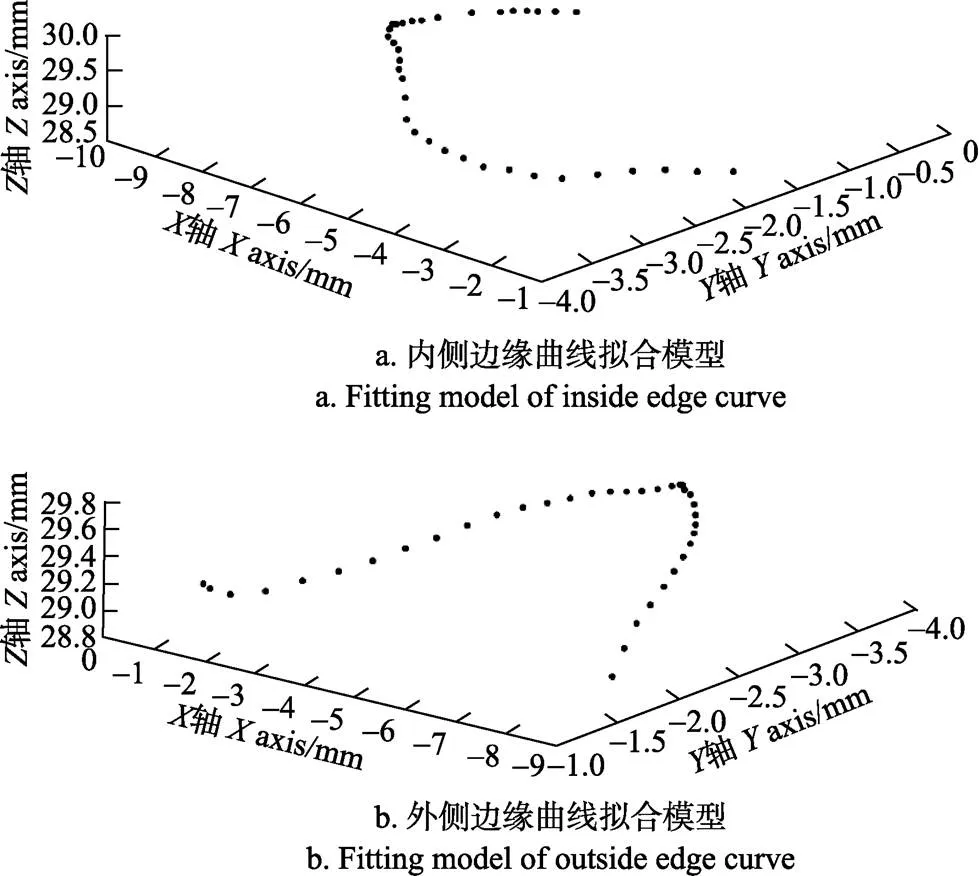
注：X轴代表提取的点云数据在X轴方向的坐标值；Y轴代表提取的点云数据在Y轴方向上的坐标值；Z轴代表提取的点云数据在Z轴方向上的坐标值,下同。

2.2 曲面数学模型

由于MATLAB工具箱（toolboxes）中的曲面拟合（surface fitting）模块不需要编程可直接对点云数据进行多项式拟合，因此脊线凹槽面和足跟凸冠面用MATLAB软件进行拟合。

2.2.1 脊线凹槽面数学模型

将脊线凹槽面坐标数据导入到MATLAB中，以为自变量，为因变量（其中，，为曲面点云的三维坐标数据），以多项式形式来拟合曲面特征点云，拟合结果如表1所示。

表1 不同指数自变量的脊线凹槽面拟合结果

分析表1可以看出，随着指数的不断增大，SSE与RMSE不断减小，2不断增大，这说明随着指数增大，方程的拟合精度越来越高。在指数为2次之后SSE与RMSE无明显减小，2无明显增加：在的指数由22增加到23时，SSE与RMSE分别减小18.14和0.07，2增加0.104；当的指数由23增加到33时，SSE减小0.6，RMSE减小0.01，2没有变化。由于每增加1个次幂数，曲面的复杂程度也会大大增大，并且考虑到拟合图形与原生物模型的相近性，选取，的指数为23时的方程，拟合方程如式（3）所示。

3=3.18-0.65+2.24-0.122+0.14+0.782-0.032+0.072+0.073（3）

式（3）的拟合参数SSE为7.36，RMSE为0.09，R为0.96。该拟合曲面继承了原生物模型的几何特征，说明该部位曲面被成功地从生物模型转换为数学模型，如图5所示。

图5 脊线凹槽处拟合曲面

2.2.2 足跟凸冠面数学模型

用同样的方法，对足跟凸冠面进行模型，所得结果如表2所示。

表2 不同指数自变量的足跟凸冠面拟合结果

分析表2，、的指数都为2时，SSE和RMSE减少很多，2增大到0.98，与,的指数均为3时基本相同，并且考虑到实际加工的复杂程度，因此选定,的指数都为2。拟合方程如式（4）所示。

4=16.64+5.00+0.86+0.362+0.18+0.432（4）

式（4）的拟合参数SSE为1.46，RMSE为0.05，R为0.98。图6为拟合的数学模型，外观如同一个凸冠状，符合原生物模型的基本特征。

图6 足跟凸冠拟合曲面

2.3 数学模型验证

为了验证建立的曲线曲面的数学模型，选取建模样本之外的同种驯鹿2个左后足作为验证样本。用三维激光扫描仪获取样本的点云数据并导入Geomagic Studio中进行数据处理得到光滑的样本三维模型。将特征部位的点云导入到CATIA中，经过过滤转化后得到2个验证样本的内外侧边缘曲线、脊线凹槽面和足跟凸冠面部位点云的三维坐标数据。将所得2个样本特征部位坐标数据的坐标值分别带入到所建立的数学模型公式中得出拟合值0，与原数据进行对比分析得出残差和相对误差，如表3所示。

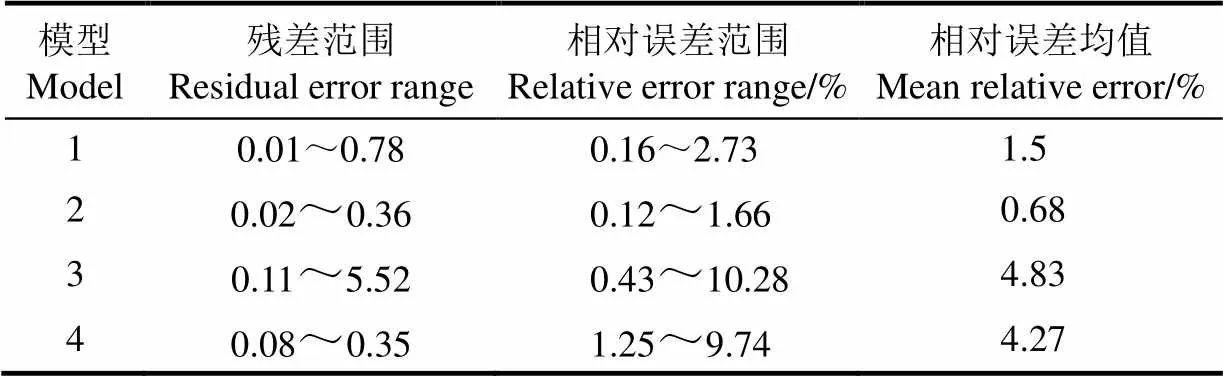
表3 不同驯鹿足特征部位的模型拟合值与实际值对比分析

注：模型1是指内侧边缘曲线；模型2是指外侧边缘曲线；模型3是指脊线凹槽面；模型4是指足跟凸冠面。

Note: Model 1 indicates inside curve-fitting model; Model 2 indicates outside curve-fitting model; Model 3 indicates fitting surface of ridge groove; Model 4 indicates fitting surface of spherical cap.

分析表3，通过拟合值0与原数据值对比分析发现，文中所建立4个数学模型的计算值与实际值的一致性良好，相对误差基本控制在10%以内。其中模型1和模型2的拟合模型最优，最大的相对误差也仅为2.73%和1.66%。两种模型的相对误差均值为1.5%和0.68%。而模型3和模型4由于拟合的是不规则曲面，则最大相对误差在10.28%。但2个模型的相对误差均值为4.83%和4.27%，总体误差较小，在工程设计上允许的误差以内（±5%）[30]，验证了该文所构建数学模型的有效性。

3 足底元素成分分析

考虑到驯鹿足不同部位的元素成分对于驯鹿在冰雪路面上的运动也有一定影响，而能谱分析对于研究材料成分具有重要作用[31-33]。因此利用Oxford公司生产的X射线光电子能谱仪对3个建模样本和2个验证样本的凸冠、脊线凹槽以及边缘部位进行2次成分测量，测量值取平均后如表4所示。

表4 驯鹿足底元素质量分数

注：“—”代表不存在。

Note: “—”indicates inexistence.

分析表4，驯鹿足底的微量元素基本由Ca、Si、Al、S、Cl、K、Fe及Mg组成，足底的不同部位的元素含量有所差别。元素Si（1.72%～4.16%）、Ca（2.43%～5.02%）和Al（1.25%～1.44%）在这些微量元素中含量最高。其中，凹槽部位的Ca和Si分别为5.02%和4.16%，均高于其他部位。边缘部位没有Mg和S存在，而Ca元素含量相对于凸冠和凹槽部位较少。除微量元素外，足底还含有大量的C（42.9%～44.54%）、N（4.86%～8.23%）和O（39.31%～41.38%）这些主要元素。凸冠及凹槽部位是以Si、Mg为主的无机成分，使得其微观组织结构更加紧密，有利于提高结构的硬度。边缘处缺少了某些元素，可能此特性会有利于其更好地切入冰面。各部位元素对驯鹿足防滑所起到的作用我们在今后将会有更深入的研究。

4 结 论

本研究通过三维激光扫描仪扫描获得了驯鹿足的三维几何模型，并通过Geomagic Studio软件对驯鹿足底进行分区处理，并分离出内、外侧边缘曲线、脊线凹槽面、足跟凸冠面4个特征部位。利用CATIA软件对特征部位进行过滤处理并得到特征点云的三维坐标数据。

用1stOpt软件对内、外侧边缘曲线进行自动曲线拟合，得到了2个三维曲线方程，决定系数分别为0.994、0.992。在MATLAB中对脊线凹槽面和足跟凸冠面2个曲面进行拟合，得到2个曲面图形以及拟合方程，决定系数分别为0.96、0.98。通过其他驯鹿蹄点云数据对数学模型进行验证，结果表明相对误差均值在5%以内，验证了模型的有效性，实现了足底特征形貌的生物模型到数学模型的转化。

分析了驯鹿足底特征部位的成分含量，在多种微量元素中Ca（2.43%～5.02%）和Si（1.72%～4.16%）元素较高，并存在于所有的特征部位中，这有利于提高驯鹿足底的硬度和耐磨性。为后期把驯鹿足底防滑特性以及足底材料属性应用到轮胎胎面上奠定了理论基础。

[1] 刘永刚，周利坤. 仿章鱼吸盘式轮胎冰面防滑机理研究[J]. 黑龙江科技信息，2013(22)：136－136.

[2] 陈旭. 改善橡胶表面摩擦学特性的仿生结构设计及试验研究[D]. 长春：吉林大学，2008. Chen Xu. Biomimetic Structure Design and Experiments for Improving the Tribological Characteristic of the Rubber Surface[D]. Changchun: Jilin University, 2008. (in Chinese with English abstract)

[3] 莽超. 普利司通BLIZZAK冰锐客XG01[J]. 汽车与运动，2015(1)：144－147.

[4] 吴中元. 白色恋人：米其林X－ICE＾X13冬季轮胎[J]. 车主之友，2012(9)：248－253.

[5] 谢立. 大陆公司展示新型冬季轮胎[J]. 橡塑技术与装备，2016，42(5)：37.

[6] 卫东. 倍耐力冰雪轮胎SCORPION WINTER[J]. 汽车与运动，2016(3)：154－155.

[7] Schallamach A. How does rubber slide?[J]. Wear, 1971, 17(4): 301－312.

[8] Anudeep K. Bhoopalam, Corina Sandu. Review of the state of the art in experimental studies and mathematical modeling of tire performance on ice[J]. Journal of Terramechanics. 2014, 53: 19－35.

[9] Anudeep K. Bhoopalam, Corina Sandu, Saied Taheri. Experimental investigation of pneumatic tire performance on ice: Part 1–Indoor study[J]. Journal of Terramechanics, 2015, 60: 43－54.

[10] Anudeep K. Bhoopalam, Corina Sandu, Saied Taheri. Experimental investigation of pneumatic tire performance on ice: Part 2–Outdoor study[J]. Journal of Terramechanics. 2015, 60: 55－62.

[11] Anudeep K. Bhoopalam, Corina Sandu, Saied Taheri. Tiretraction of commercial vehicles on icy roads[J]. SAE International Journal of Commercial Vehicles, 2014, 7(2): 357－365.

[12] Bhoopalam A K，Sandu C，Taheri S. A tire–icemodel (TIM) for traction estimation[J]. Journal of Terramechanics, 2016, 66: 1－12

[13] 彭旭东，郭孔辉. 橡胶和轮胎的摩擦[J]. 橡胶工业杂志，2003，50(9)：562－568.

[14] 彭旭东，雷毅，郭孔辉，等. 冰雪路面上轮胎摩擦特性的控制方法研究[J]．中国机械工程，2001，12(11)：30－33. Peng Xudong, Lei Yi, Guo Konghui, et al. Study on the control methods for tire traction characteristics on icy/snowy highways[J], China Mechanical Engineering. 2001, 12(11): 30－33. (in Chinese with English abstract)

[15] 彭旭东，宗长富，谢友柏，等. 冰面上轮胎摩擦牵引力的实验研究[J]. 摩擦学学报，2000，20(1)：32－35. Peng Xudong, Zong Changfu, Xie Youbai, et al. Experimental study of indoor tire traction force on ice[J]. Tribology, 2000, 20(1): 32－35. (in Chinese with English abstract)

[16] 彭旭东，谢友柏. 接地面全熔化条件下冰面轮胎摩擦力的预测[J]. 汽车工程，1999，21(4)：193－198． Peng Xudong, Xie Youbai. Prediction of tire friction on icing road with fully melting contact patch[J]. Automotive Engineering, 1999, 21(4): 193－198. (in Chinese with English abstract)

[17] 彭旭东，谢友柏，郭孔辉. 轮胎摩擦学的研究与发展[J]. 中国机械工程，1999，10(2)：215－219. Peng Xudong, Xie Youbai, Guo Konghui. The investigation and development trends of tire tribology[J]. China Mechanical Engineering, 1999, 10(2): 215－219. (in Chinese with English abstract)

[18] 彭旭东，谢友柏，郭孔辉. 一套预测冰面上汽车牵引力的模型[J]. 摩擦学学报，1998，18(4)：351－355. Peng Xudong, Xie Youbai, Guo Konghui. A model for prediction of automobile traction on ice[J]. Tribology, 1998, 18(4): 351—355. (in Chinese with English abstract)

[19] 彭旭东，谢友柏. 冰雪路面汽车轮胎的摩擦机理研究[J]. 汽车技术，1998(4): 10－13.

[20] 周利坤，王洪伟. 仿章鱼吸盘式轮胎花纹设计与有限元分析[J]. 西安理工大学学报，2013，29(2)：228－232. Zhou Likun, Wang Hongwei. Imitation octopus sucker—type tire tread pattern design and finite element analysis[J]. Journal of Xi’an University of Technology, 2013, 29(2): 228－232. (in Chinese with English abstract)

[21] 刘永刚，周利坤. 仿章鱼吸盘式轮胎弹塑性黏着接触性能研究[J]. 机械设计与制造，2013(12)：238－241. Liu Yonggang, Zhou Likun. Research on the performance of elastic—plastic adhesive contact of octopus sucker type tire[J]. Machinery Design & Manufacture, 2013(12): 238－241. (in Chinese with English abstract)

[22] 周利坤，王洪伟. 基于ADAMAS的仿章鱼吸盘式轮胎防滑性能仿真分析[J]. 橡胶工业，2014，61(7)：426－429. Zhou Likun, Wang Hongwei. Simulation Analysis on Anti—skid Performance of Bionic Tire by ADAMS[J]. China Rubber Industry, 2014, 61(7): 426－429. (in Chinese with English abstract)

[23] 常悦，张玉，陈巴特尔，等. 驯鹿及其生物学特性研究[J]. 家畜生态学报，2013，34(2)：84－87. Chang Yue, Zhang Yu, Chen Bateer, et al. Reindeer and its biology characteristics[J]. Acta Ecologiae Animalis Domastici, 2013, 34(2): 84－87. (in Chinese with English abstract)

[24] 李杰，庄继德，魏东. 沙漠用仿驼蹄橡胶轮胎的设计与试验研究[J]. 农业工程学报，1999，15(2)：32－37． Li Jie, Zhuang Jide, Wei Dong. Design and test of the bionic camel foot rubber tire for desert vehicles[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1999, 15(2): 32－37. (in Chinese with English abstract)

[25] Banfieldal A W F. The plight of the barren ground Caribou[J]. Oryx, 1957, 4(1): 5－20.

[26] 张锐，杨明明，潘润铎，等．鸵鸟足底非规则曲面形貌数学模型构建[J]．农业工程学报，2015，31(增刊1)：71－78． Zhang Rui, Yang Mingming, Pan Runduo. et al. Mathematical model establishment of irregular plantar surface of ostrich didactyl foot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(Supp.1): 71－78. (in Chinese with English abstract)

[27] 李世武，佟金，张书军，等．牛蹄三维几何模型逆向工程研究[J]．农业工程学报，2004，20(2)：156－160．Li Shiwu, Tong Jin, Zhang Shujun, et al. Three—dimensional geometrical modeling of the exterior configuration of a cattle hoof by reverse engineering technology[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2004, 20(2): 156－160. (in Chinese with English abstract)

[28] 张永智，左春柽，孙少明，等．水田驱动叶轮仿生叶片机理数值模拟分析[J]．农业机械学报，2008，39(11)： 176－179． Zhang Yongzhi, Zuo Chuncheng, Sun Shaoming, et al. Numerical simulation on bionic blade of paddy impeller[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(11): 176—179. (in Chinese with English abstract)

[29] 董洽. 基于1stOpt的二级圆柱齿轮减速器优化设计[J]．机械传动，2012，36(7)：69－71. Dong Qia. Optimization design of two—stage cylindrical gear reducer based on 1stOpt[J]. Journal of Mechanical Transmission, 2012, 36(7): 69－71. (in Chinese with English abstract)

[30] Yin Hanfeng, Xiao Youye, Wen Guilin, et al. Crushing analysis and multi—objective optimization design for bionic thin—walled structure[J]. Materials and Design, 2015, 87: 825－834.

[31] 高吭，李玉柱，佟金，等．东方蝼蛄口器结构与表皮纳米力学性能研究[J]．农业机械学报，2011，42(8)：224－227． Gao Hang, Li Yuzhu, Tong Jin, et al. Microstructure and nanoindentation properties of mouthparts of oriental mole cricket[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(8): 224－227. (in Chinese with English abstract)

[32] 马云海，佟金，周江，等. 穿山甲鳞片表面的几何形态特征及其性能[J]．电子显微学报，2008，27(4)：336－340． Ma Yunhai, Tong Jin, Zhou Jiang, et al. Geometric shape and performance of the scale of the pangolin[J]. Journal of Chinese Electron Microscopy Society, 2008, 27(4): 336－340. (in Chinese with English abstract)

[33] 许顺，佟金，马云海，等. 基于ANSYS的竹象虫头管仿生模型抗扭转分析[J]. 农业工程学报，2016，32(12)：11—16． Xu Shun, Tong Jin, Ma Yunhai, et al. Torque analysis on bionic model of bamboo weevil rostrum based on ANSYS[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(12): 11－16. (in Chinese with English abstract)

Mathematical model establishment and validation of irregular characteristic morphology for reindeer foot bottom

Zhang Rui, Qiao Yu, Ji Qiaoli, Li Jianqiao

(130022,)

In recent years, the traffic accidents occur frequently in winter and how to prevent frequent traffic accidents has become an urgent problem to be solved. Reindeer lives in frigid areas and possesses the superior walking ability on ice. Reindeer feet are the exclusive parts which contact with the ice directly. The sole characteristic morphology of foot bottom is the key factor to the excellent anti-skid performance of reindeer. The research of the reindeer feet bottom characteristics will help to apply the superior characteristics to snow tire tread and improve the trafficability property of tire on ice ground. Therefore, the mathematical models of the reindeer feet were studied. The feet were taken from 4 eighteen-year-old adult homebred reindeers, which were bought from the Ewenki nationality located in Genhe City, Inner Mongolia, China. In order to avoid impurity interference, the feet were cleared up before the experiments. The geometric point clouds of the reindeer feet were obtained by using a three-dimensional (3D) hand-held non-contact laser scanner. After that, the data were imported to Geomagic Studio software and we reconstructed the analytical model. With the cutting function of the software, the reconstructed model of reindeer foot was divided into 4 typical characteristic areas: The edge curves (inside edge and outside edge), the ridge groove surface and spherical cap surface. In addition, these point clouds were imported to CATIA (computer aided three-dimensional interactive application) to be filtered, which reduced the calculation amount of the fitting curves and surfaces. We filtered the dense point clouds through adopting the reasonable method and the retained characteristic points that reflected the edge and sole morphology of reindeer foot with the digitized shape editor module of CATIA. Through the above processes, the 3D coordinate data points of these characteristic areas were exported. The edge curves were fitted using curve fitting software 1stOpt (First Optimization), and then fitting the equation and the fitted parameters were acquired, respectively. We also used the surface fitting function of Matlab software to fit 2 surfaces: Ridge groove surface and spherical cap surface. Finally, 2 surface fitting models were achieved. The fitting results revealed that the2(coefficient of determination) values of 2 curves and 2 surfaces were 0.994, 0.992, 0.96, and 0.98, respectively, which were all close to 1. It showed that the characteristic areas of reindeer feet were successfully transformed from the biological model to the mathematical model. In order to verify the model’s scientificity, the specimen of other reindeer foot was used. We acquired the 3D coordinate data of the same characteristic areas of other reindeer foot by adopting the same treatment. The values ofandaxis for 4 areas were imported into relevant mathematical models and the relevant values that were dependent variables were acquired. By comparing the differences between fitting values and actual values, the residual error range, relative error range and mean relative error were analyzed. The relative error range of 2 curves models was 0.16%-2.73% and 0.12%-1.66% respectively, and the mean relative error was 1.5% and 0.68%, respectively. The relative error range of surfaces models was 0.43%-10.28% and 1.25%-9.74%, respectively. The maximum was about 10%, due to the influence of air impurities. However, the mean relative errors of surfaces models were 4.83% and 4.27%, respectively. The mean relative errors of 4 models were within 5%, which proved the mathematical models’ effectiveness in this paper. In addition, the elements of reindeer feet were examined with EDS (energy dispersive spectroscopy). It included such elements as S, Si, Fe, Al, K and Ca, besides C, O and N. Different chemical elements meant different compounds, and different surfaces with different skid-resistance were composed of different elements. This paper will provide research direction for studying tire on ice ground with engineering bionic technology.

bionic; models; computer simulation; reverse engineering; plantar surface of reindeer foot

10.11975/j.issn.1002-6819.2017.08.007

TB17

A

1002-6819(2017)-08-0056-06

2016-07-27

2017-01-23

国家自然科学基金资助项目（51275199）；陆军及通用武器装备技术革新项目（2014220101001105）

张 锐，男，吉林磐石人，教授，博士生导师，主要从事松软地面仿生行走及数值计算研究。长春 吉林大学工程仿生教育部重点实验室，130022。Email：zhangrui@jlu.edu.cn

张 锐，乔 钰，吉巧丽，李建桥. 驯鹿足底非规则特征形貌数学模型构建及验证[J]. 农业工程学报，2017，33(8)：56－61. doi：10.11975/j.issn.1002-6819.2017.08.007 http://www.tcsae.org

Zhang Rui, Qiao Yu, Ji Qiaoli, Li Jianqiao. Mathematical model establishment and validation of irregular characteristic morphology for reindeer foot bottom[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(8): 56－61. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.08.007 http://www.tcsae.org