基于功率及频率波动相位的强迫扰动源定位

蒋 平，郑斌青，冯 双

（东南大学 电气工程学院，江苏 南京 210096）

0 引言

我国电力系统飞速发展，已初步形成“西电东送，南北互供，全国联网”的大区电网互联的局面［1］。在电网可靠性得到提高、资源配置得到优化的同时，低频振荡问题也成为影响电力系统安全稳定运行的关键问题。关于低频振荡的起因，除了传统观点上的系统存在负阻尼会引起低频振荡，越来越多的研究发现持续性的周期小扰动会引发系统的强迫振荡［2-4］，且当振荡频率与系统的固有频率相等时，系统功率振荡幅值达到最大。强迫振荡具有明确的扰动源，起振快，表现为持续的等幅振荡，当扰动源切除后，振幅迅速衰减。因此，快速准确地定位扰动源是抑制强迫振荡首先需要考虑的问题。

实际电网发生强迫振荡时，扰动源很难及时被发现和切除，扰动源的定位受到了国内外学者越来越多的关注。文献［5-7］基于能量函数计算网络中的振荡能量，根据能量的转换识别定位电网强迫扰动源。文献［8-9］构建了不同层次的割集，根据割集流出的振荡能量正负来判断扰动源是否位于割集内部，实现扰动源大致方位的识别。文献［10］基于能量趋势函数计算出的量化指标来判断扰动源位置，在能量函数法的基础上做了改进，能够提高定位的准确性。文献［11］提出基于广域测量系统（WAMS）的空间特征椭球和决策树混合定位扰动源的新方法。文献［12］采用滑动数据窗法计算机电波到达时间来确定扰动源的位置，引进了机电波在振荡源定位方面的应用，提高了定位的快速性。

广域测量系统的广泛建设为扰动源的定位提供了有效的技术手段。本文基于同步发电机转子方程，对发电机的机械功率波动、输出电气功率波动及角频率波动间的相量关系进行理论分析，给出了通过比较输出电气功率波动和角频率波动之间的相位关系判断扰动源是否位于发电机上的理论依据；在此基础上分析网络中线路上的电气量波动的相位关系，提出一种通过比较频率波动与有功功率波动之间的相位关系，判断支路上的振荡能量流向进行扰动源定位的方法。采用最小二乘法旋转不变（TLS-ESPRIT）算法提取出主导频率下电气波动量的相位参数，能够直接利用振荡初始阶段获取的数据，消除了采集的电气量中非扰动源决定的分量，提高了扰动源定位的准确性。此外，本文方法基于广域测量系统实测数据直接识别频率和有功功率这2个电气量的相位参数并进行判断，相对传统的能量函数法，更加简洁、直观，降低了系统在线监测分析的复杂性。

1 强迫振荡系统的能量特性

假设电力系统在机械功率扰动ΔPm=Acos（ωt）的扰动下发生强迫振荡，在平衡点附近线性化之后的发电机运动方程为：

其中，M为发电机的惯性常量；Δδ为发电机功角相对于平衡点的偏移量；D为发电机阻尼系数；ΔPe为发电机输出电气功率波动。

根据暂态能量函数建立的方法［6］，对式（1）进行积分，可得：

在电力系统发生强迫振荡且达到稳态时，功角波动量、功率波动量、频率波动量等都能够用正弦函数来表示［2］。则式（2）中各个部分在振荡周期内的平均函数为：

其中，T为系统强迫振荡的周期。

由式（3）可知，系统振荡过程中，外施扰动注入的能量在发电机阻尼上消耗一部分之后，剩余的振荡能量从发电机流向系统。

2 强迫振荡定位方法

2.1 发电机上扰动源的定位

设某一机组原动机上产生机械功率扰动，从而引起电力系统发生强迫振荡。将式（1）转换为相量形式，可表示为：

其中，ΔPm、ΔPe、Δω 分别为机械功率波动 ΔPm、电气功率波动ΔPe以及角频率波动Δω的相量形式；Ω=2π/T。

根据式（4）可得，振荡稳态阶段发电机机械功率波动ΔPm、输出电气功率波动ΔPe以及角频率波动Δω的相量关系如图1所示。

图1 振荡过程中 ΔPm、ΔPe、Δω 的相量关系图Fig.1 Phasor relationship among ΔPm，ΔPeand Δω during oscillation

图1中，α为ΔPe相对于Δω的波动相位；β为ΔPm相对于Δω的波动相位。由式（4）可以知道，相量 jΩ MΔω+DΔω、ΔPe和 ΔPm组成一个相量三角形，由图1可得Δω的相位超前于ΔPe的相位，且相位差 α＜90°。

由图1可知：当β增大时，α也随之增大，直至α=90°，即表示单机无穷大系统发生强迫振荡时的相量图；当D减小时，ΔPe首端从点b向点a移动，ΔPe的幅值也随之增大，且其在Δω正方向的投影也随之增大。因此，增大阻尼系数D是能够抑制强迫振荡的直接手段。

如果扰动源不在原动机上，此时有：

其中，K（s）为原动机及调速器的传递函数，具有负实部［13］。式（5）表示原动机只含有由于转速反馈控制产生的机械功率波动，代入式（4）后，稳态阶段机械功率波动ΔPm、输出电气功率波动ΔPe和角频率波动Δω的相量关系如图2所示。

图2 扰动源不在原动机上时振荡过程中ΔPm、ΔPe、Δω 的相量关系图Fig.2 Phasor relationship among ΔPm，ΔPeand Δω during oscillation when prime mover is not disturbance source

图2中，ΔPm位于第二象限，由此可得α＞90°。

根据以上分析，可得扰动源是否位于发电机上的判据为：

其中，φω、φPe分别为发电机角频率波动的相位和输出电气功率波动的相位。如果式（6）成立，那么扰动源位于发电机上；否则，扰动源不在发电机上。

2.2 网络支路（非发电机）母线上扰动源的定位

根据第1节分析可知，发电机上扰动源注入的振荡能量除了消耗在阻尼上，剩余的能量向外输出。2.1节根据发电机输出电气功率波动ΔPe与角频率波动Δω之间的相位关系判断扰动源是否位于发电机上，实际反映出发电机振荡能量的流向，若发电机是扰动源，则振荡势能从发电机流出；反之，则流入发电机。

在高压输电线中，电抗远远大于电阻，所以电阻可以忽略不计。由于电压幅值与有功功率的耦合非常小，因此在有功功率发生振荡时，节点电压幅值可看作不变。

假设一条与发电机相连的支路为Lei，j。虽然发电机所在母线以及变压器的等值电阻不可省略，但其等效电阻与电抗的比值仍然较小，对Lei，j上有功功率波动影响非常小，几乎可以忽略不计。将线路Lei，j上的有功功率表达式线性化之后，可得：

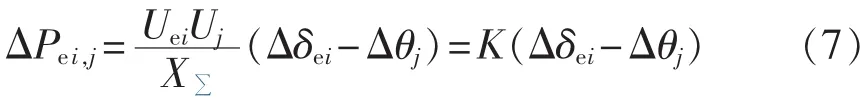
其中，Uei、Uj分别为发电机机端电压以及节点j的电压；X∑为支路的电抗；Δδei、Δθj分别为发电机内节点电压相角波动和节点j的电压相角波动；ΔPei，j为线路上的有功功率波动（发电机输出的电气功率波动）；K=UeiUj/X∑。

对式（7）两边求导，并用相量表示为：

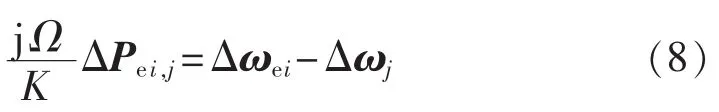
其中，Δωei、Δωj分别为发电机内节点角频率波动Δωei和节点j的角频率波动Δωj的相量形式。

分别在发电机为扰动源以及发电机不是扰动源的情况下，即振荡能量在Lei，j上从发电机流向节点j以及从节点j流向发电机，作出式（10）对应的相量图，分别如图 3、图 4 所示。 图 3、4 中，α1为 ΔPei，j与Δωj之间的夹角。 图 3 中，α1＜90°，节点 j上的振荡能量的流向与有功功率流向一致。可以发现，随着Ω/K 的大小变化，Δωj的相位从超前 ΔPei，j的相位变成滞后 ΔPei，j的相位。 图 4 中，α1＞90°，节点 j上振荡能量的流向与有功功率流向相反。

图3 发电机是扰动源时振荡过程中 ΔPei、Δωei、Δωj的相量关系图Fig.3 Phasor relationship among ΔPei，Δωei，Δωjduring oscillation when generator is disturbance source

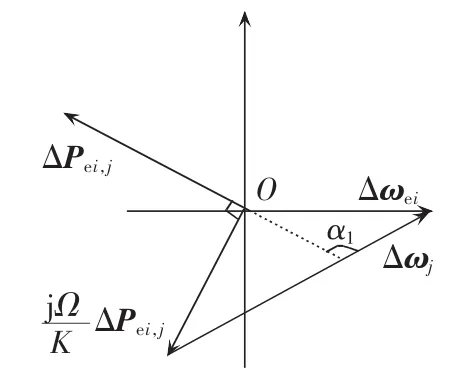
图4 发电机不是扰动源时振荡过程中 ΔPei、Δωei、Δωj的相量关系图Fig.4 Phasor relationship among ΔPei，Δωei，Δωjduring oscillation when generator is not disturbance source

将式（8）用时域表示并对两边进行积分，可得：

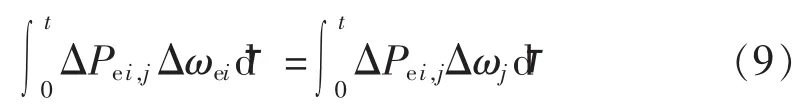
从式（9）可以发现，振荡能量随着支路节点电压角频率变化和传输的有功功率变化而沿着支路流动，母线电压角频率偏差Δωj与支路有功功率偏差ΔPei，j之间的相量关系反映了振荡能量流向。其中，节点频率偏差 Δfi=Δωi/（2π），因此 Δfi与 Δωi同相位。可将2.1节中的判据推广到网络中不含发电机母线的支路上，即：

其中，φfi、φPij分别为节点电压频率波动量的相位和与节点相连支路上的有功功率波动的相位。如果式（10）成立，那么支路上振荡能量的流向与有功功率流向一致；否则，振荡能量的流向与有功功率流向相反。振荡过程中，电压幅值的波动很小，对有功波动的影响可以忽略不计。对于一般线路而言，由于电阻的存在，会使相位差发生变化，但偏差非常小且不影响判据的判定结果。

周期性负荷扰动等效于对发电机施加一个与周期性负荷扰动同步的强迫项。因此，当扰动源位于负荷上时，上述方法仍能实现扰动源的准确定位。

3 强迫振荡的在线监测定位

3.1 基于TLS-ESPRIT算法获取波动相位

第2节中强迫振荡源的定位是对振荡的稳态阶段的波动相位关系进行分析，而电力系统在发生强迫振荡的初始阶段，除了含有由扰动引起的稳态分量，还包含由初始条件引起的瞬态分量。在电力系统实际振荡过程中，判断振荡进入稳态阶段的时间点是比较困难的，而且如果系统的固有频率较低或阻尼较弱，振荡的过渡时间会比较长。因此需要尽快获取电气波动的稳态量。

设波动信号f（n）可以表示为一系列幅值按指数规律变化的正弦信号与白噪声的组合，在采样时刻n，其表达式为：

其中，Ts为采样周期；由于采样信号为实信号，N通常为信号实际含有的实正弦分量个数的 2 倍；ai、φi、ωi、σi分别为第i个衰减分量的幅值、初始相位、角频率和衰减系数；w为均值为0的白噪声。

TLS-ESPRIT算法是ESPRIT算法的扩展，是一种基于子空间的高分辨率信号分析方法［14］。利用相量测量单元（PMU）监测获取的实时数据，TLS-ESPRIT算法能够计算出信号中各分量的频率大小、衰减系数及阻尼比，通过最小二乘法求取信号幅值和初始相位。因此可以提取出强迫振荡的主导频率即共振频率，获取相应的波动相位。而且如果实测的数据中含有异常数据，经过预处理剔除之后，TLS-ESPRIT算法仍能够准确地进行模态分析。

3.2 振荡源定位流程

根据以上分析，可以基于广域测量系统获得的实测数据，根据模态的辨识结果，得到扰动源的在线监测定位方法，步骤主要分为3步：（1）数据预处理，剔除异常数据；（2）获取相位，比较相位关系并判断支路振荡能量流向；（3）判断支路振荡能量是否都流出该母线，若是则振荡源位于该母线上。振荡源定位流程如图5所示。

4 算例分析

本文分别在4机2区系统和实际系统中进行仿真分析，验证本文提出方法的可行性及有效性。

4.1 4机2区系统

4机2区系统的结构图［15］如图6所示。根据小干扰分析可知，该系统包含1个区间振荡模式，频率为0.64 Hz。从0 s开始对该模式的强相关机组G1额外施加持续性的原动机功率扰动，扰动频率为0.64 Hz，扰动幅值为0.01 p.u.，仿真时间为20 s。此时，系统区域间发生强迫振荡，区域间联络线上有功功率P12的波动曲线如图7所示。

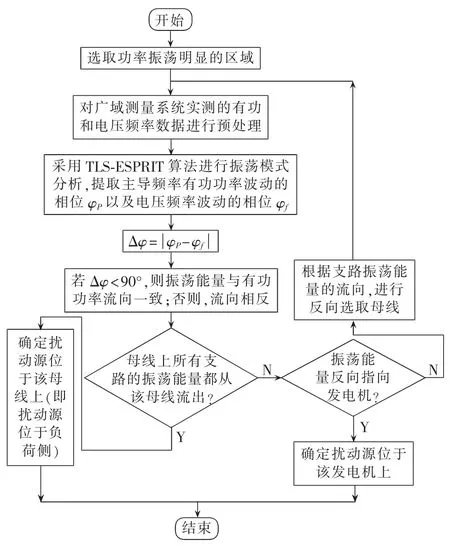
图5 扰动源在线监测定位流程图Fig.5 Flowchart of online disturbance source monitoring and locating

图6 4机2区系统Fig.6 Four-generator two-area system

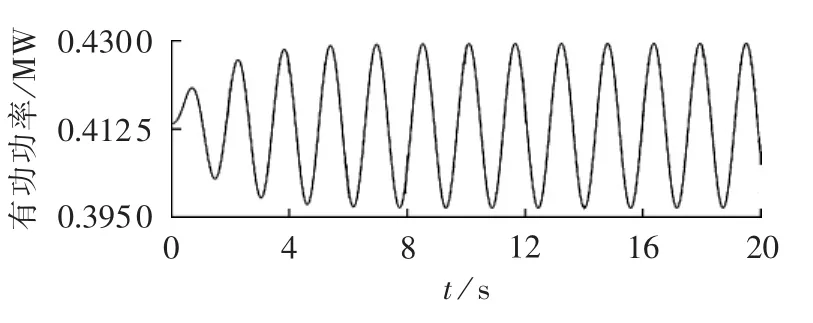
图7 联络线有功功率振荡波形Fig.7 Oscillation waveform of tie-line active power

TLS-ESPRIT算法获取主导振荡频率下的波动相位并进行能量流向判断，其结果如表1所示。

由表1中判别结果，首先根据节点7的频率波动与支路7-8上有功波动的相位差的绝对值为49°，可以判断联络线7-8上的振荡能量与有功方向一致，振荡能量从区域1流向区域2，故判定扰动源位于区域1；同理，分别进行机组出线G1-1和G2-2上支路振荡能量流向判别，振荡能量从发电机G1流出，而从发电机G2流入，故可判断扰动源位于发电机G1上，与实际情况相符合。

表1 波动相位及其判别结果Table1 Fluctuation phase-angles and recognition results

如果在系统发生振荡过程中，测量数据存在异常，数据进行预处理后用TLS-ESPRIT算法进行模态辨识，曲线拟合结果如图8所示。获取主导频率下的相位 φP7-8=163.4°。

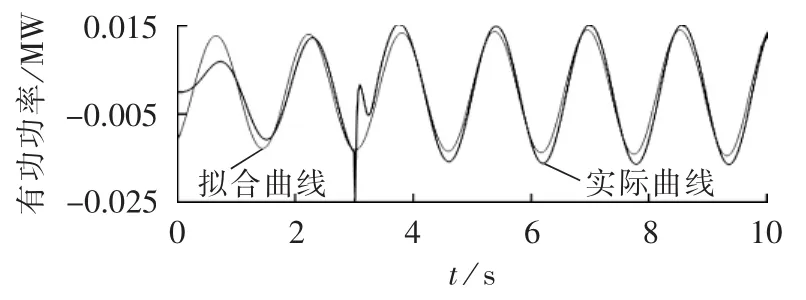
图8 振荡模态辨识曲线拟合结果Fig.8 Result of curve-fitting by oscillation mode identification

同理，获得主导频率下相应节点频率波动相位φf7=116.7°，求得相位差的绝对值为 46.7°，这与计算结果49°相差不大，仍能够正常判断出振荡能量的走向，实现扰动源的准确定位。

4.2 实际区域电网仿真分析

现以某区域电网在某种常见运行方式下进行仿真，其局部接线图如图9所示。

图9 实际电网局部接线图Fig.9 Partial diagram of actual power system

经过小干扰稳定分析得到某台发电机强相关的局部振荡模式，频率为0.8 Hz。在该台发电机附近的负荷母线上施加幅值为0.1 p.u.、扰动频率为0.8 Hz的持续性波动负荷，此时该系统发生强迫振荡。根据功率波动的情况，选取振荡情况较明显的支路进行分析。判别结果如表2所示。根据表2，首先分析支路SYL-SYLB和SYL-STW，获得有功波动相位与节点电压频率波动相位之差的绝对值分别为52.5°和65°，可以发现振荡能量流向与有功流向一致，从母线STW流入母线SYL，又从母线SYL流入母线SYLB，并由母线SYLB流向其他母线节点。

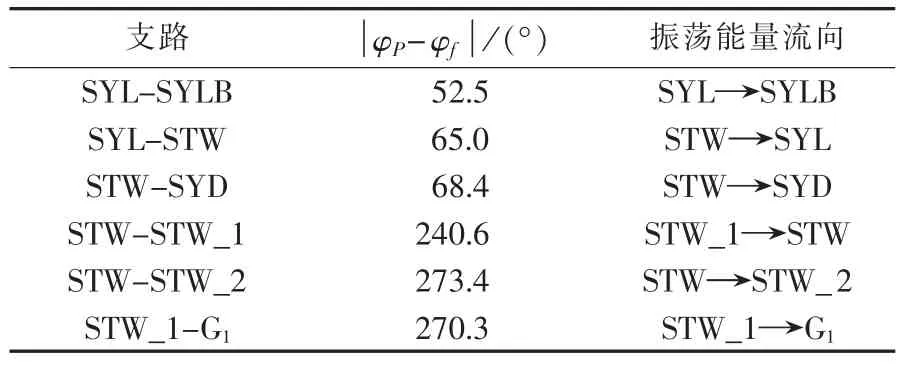
表2 波动相位及其判别结果Table2 Fluctuation phase-angles and recognition results

根据振荡能量流向逆向选取母线STW。再分析支路 STW-SYD、STW-STW_1及 STW-STW_2，根据相位差判据可以发现振荡能量由母线STW流入母线SYD和STW_2，由母线STW_1流向母线STW。

反向选取母线STW_1，分析支路STW_1-G1，根据相位差可以发现振荡能量由母线STW_1流入发电机G1。因此，可判断扰动源位于负荷母线STW_1上，与实际情况一致。

5 结论

本文从有功功率波动和电压频率波动之间的相量关系角度，采用相量法进行理论分析，给出了振荡能量的流向判据，从而实现强迫扰动源的定位。通过在4机2区系统以及实际区域电网仿真，验证了该方法的可行性及有效性。本文定位方法采用TLSESPRIT算法提取出主导频率下的相位信息，能够消除瞬态阶段自由分量以及异常数据对判别结果的影响。该方法只需获取支路有功功率以及母线电压频率的数据，均来自于母线上PMU的实测数据，从而能够具体对网络某条支路进行分析。该定位方法简单、直观，最大限度地减少了在线监测分析的复杂性。

此外正确区分振荡性质并进行识别定位扰动源，将会提高定位方法的应用广泛性以及实用性，这也将成为下一步研究的重要内容。

［1］邓集祥，贺建明.大区域联网条件下四川电网低频振荡分析［J］.电网技术，2008，32（17）：78-82.DENG Jixiang，HE Jianming.Analysis of low frequency oscillation for Sichuan Power Grid in large scale interconnected power systems［J］.Power System Technology，2008，32（17）：78-82.

［2］汤涌.电力系统强迫功率振荡的基础理论［J］.电网技术，2006，30（10）：29-33.TANG Yong.Fundamental theory of forced power oscillation in power system［J］.Power System Technology，2006，30（10）：29-33.

［3］余一平，闵勇，陈磊.多机电力系统强迫功率振荡稳态响应特性分析［J］.电力系统自动化，2009，33（22）：5-9.YU Yiping，MIN Yong，CHEN Lei.Analysis of forced power oscillation steady-state response properties in multi-machine power systems［J］.Automation of Electric Power Systems，2009，33（22）：5-9.

［4］余一平，闵勇，陈磊，等.周期性负荷引发强迫功率振荡分析［J］.电力系统自动化，2010，34（6）：7-11.YU Yiping，MIN Yong，CHEN Lei，et al.Analysis of forced power oscillation caused by continuous cyclical load disturbances［J］.Automation of Electric Power Systems，2010，34（6）：7-11.

［5］JING C，MACALLEY J D，KOMMAREDD Y M.An energy approach to analysis of interarea oscillations in power systems［J］.IEEE Transactions on Power Systems，1996，11（2）：734-740.

［6］余一平，闵勇，陈磊，等.基于能量函数的强迫功率振荡扰动源定位［J］.电力系统自动化，2010，34（5）：1-6.YU Yiping，MIN Yong，CHEN Lei，et al.Disturbance source location of forced power oscillation using energy functions［J］.Automation of Electric Power Systems，2010，34（5）：1-6.

［7］CHEN Lei，MIN Yong，HU Wei.An energy-based method for location of power system oscillation source［J］.IEEE Transactions on Power Systems，2012，28（2）：828-836.

［8］李文锋，郭剑波，李莹，等.基于WAMS的电力系统功率振荡分析与振荡源定位（1）割集能量法［J］.中国电机工程学报，2013，33（25）：41-46.LI Wenfeng，GUO Jianbo，LI Ying，et al.Power system oscillation analysis and oscillation source location based on WAMS part 1：method of cutset energy［J］.Proceedings of the CSEE，2013，33（25）：41-46.

［9］王娜娜，廖清芬，唐飞，等.基于割集能量及灵敏度的强迫功率振荡扰动源识别［J］.电力自动化设备，2013，33（1）：78-80.WANG Nana，LIAO Qingfen，TANG Fei，et al.Disturbance source identification based on cutset energy and sensitivity for forced power oscillation［J］.Electric Power Automation Equipment，2013，33（1）：78-80.

［10］褚晓杰，印永华，高磊，等.基于经验模态理论的强迫振荡扰动源定位新方法［J］.中国电机工程学报，2014，34（28）：4906-4912.CHU Xiaojie，YIN Yonghua，GAO Lei，et al.A new forced oscillation disturbance source location method based on empirical mode theory［J］.Proceedings of the CSEE，2014，34（28）：4906-4912.

［11］蒋长江，刘俊勇，刘友波，等.基于广域测量系统和CELL理论的强迫振荡在线感知与定位［J］.电力自动化设备，2015，35（2）：125-131.JIANG Changjiang，LIU Junyong，LIU Youbo，et al.Online forced oscillation detection and identification based on wide area measurement system and CELL theory［J］.Electric Power Automation Equipment，2015，35（2）：125-131.

［12］燕跃豪，毕天姝，杨奇逊.一种基于机电波理论的电网扰动在线定位方法［J］.华北电力大学学报，2014，41（1）：1-6.YAN Yuehao，BI Tianshu，YANG Qixun.An on-line disturbance location algorithm for power networks based on the electromechanical waves theory［J］.Journal of North China Electric Power University，2014，41（1）：1-6.

［13］王茂海，孙昊.强迫功率振荡的在线定位分析技术［J］.中国电机工程学报，2014，34（34）：6209-6215.WANG Maohai，SUN Hao.An analysis method for forced power oscillation source detection［J］.Proceedings of the CSEE，2014，34（34）：6209-6215.

［14］张静，徐政，王峰，等.TLS-ESPRIT算法在低频振荡分析中的应用［J］.电力系统自动化，2007，31（20）：84-88.ZHANG Jing，XU Zheng，WANG Feng，et al.TLS-ESPRIT based method for low frequency oscillation analysis in power system［J］.Automation of Electric Power Systems，2007，31（20）：84-88.

［15］KUNDUR P.Power system stability and control［M］.New York，USA：Mc Graw-Hill，Inc.，1994：548-551.