特高压直流分层接入方式下稳态特性研究

付 蓉 ，孙万钱 ，汤 奕 ，周振凯

（1.南京邮电大学 自动化学院，江苏 南京 210023；2.东南大学 电气工程学院，江苏 南京 210096）

0 引言

随着特高压直流工程的建设，我国华东电网和南方电网出现了多馈入交直流系统，但多馈入直流系统存在对受端电网电压支撑能力要求较高、不能根据需求引导功率合理分配等问题。与多馈入直流输电方式相比，特高压直流分层接入方式即逆变侧分别接入1000 kV和500 kV电压等级电网，具有工程造价低、能提升电网安全稳定运行等特点；能提升受端电网电压支撑能力；通过引导输送的直流功率在不同受端回路进行合理分配，能够充分发挥两级电网的输电能力［1］。

但特高压直流分层接入方式作为一种创新型的接入方式，目前国内外尚没有实例，所以需对这种接入方式进行研究。换流母线电压相互作用因子MIIF（Multi-Infeed Interaction Factor）以及短路比 SCR（Short Circuit Ratio）是评价直流输电系统强度与交互影响分析的重要指标［2］。

文献［2-3］分析了直流控制方式和交直流参数对多馈入直流系统电压相互作用因子的影响。文献［4］主要讨论了高压直流输电系统换相失败特性。文献［5］分析了换相失败的机理原因，并提出了特高压直流输电系统中避免换相失败的措施。文献［6-7］讨论了多馈入相互作用因子与直流子系统同时发生换相失败的关系。文献［8］提出了用电压稳定耦合因子作为衡量多馈入直流输电系统换流母线间影响的指标。文献［9-10］详细推导了多馈入短路比影响因素以及其与相互作用因子之间的关系。但上述文献大多是分析多馈入系统或高压直流输电系统的，并不完全适用于直流分层接入时相互作用因子与短路比的分析求解。

本文在特高压直流分层接入方式下对其换流母线电压相互作用因子、短路比以及接入不同受端系统系统潮流重新分布进行分析，同时针对一条回路上换流器换相失败对另一条回路上换流器的换相影响进行研究。

1 特高压直流分层接入交直流系统稳态方程

特高压直流分层接入方式如图1所示。图中，采用2组12脉动换流器串联的形式分别与三绕组变压器相连并接往不同电压等级母线上；Id为直流电流；Ud1与Ud2分别为回路1和2的逆变侧直流电压；Ud为整个逆变侧直流电压，即Ud1与Ud2之和；U1和 U2为不同电压等级逆变侧交流母线线电压有效值；T1和T2为变压器变比；Z1和Z2为交流系统等值阻抗；Z12为换流母线1和2之间的等值联系阻抗；Iac1与Iac2分别为特高压直流分层接入方式下从1000 kV和500 kV直流换相母线注入受端电网的交流电流；E1∠ ζ1、E2∠ ζ2为受端系统恒压源；Bc1、Bc2分别为回路1和回路2的无功补偿设备；Pd1、Pd2分别为输送到回路1、2的直流有功功率；Pac1、Pac2分别为输送到交流受端系统回路1、2的有功功率；P12为换流母线间联络线上功率；Pd为直流输电线路上有功功率。

图1 特高压直流分层接入方式示意图Fig.1 Schematic diagram of UHVDC hierarchical connection mode

在不考虑系统线路损耗的条件下，建立图1所示的特高压直流分层接入方式下系统逆变侧电压与功率方程分别如式（1）和式（2）所示。

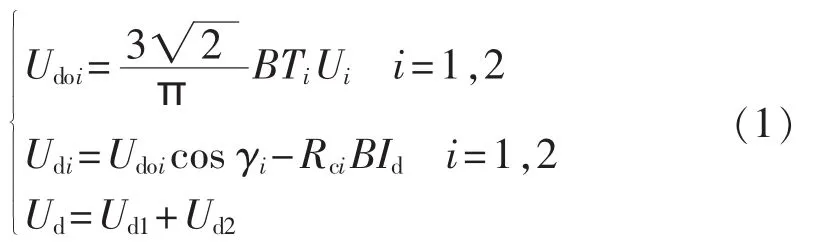
其中，Udo1、Udo2分别为回路1和2换流器的理想空载直流电压；B为6脉动换流器的个数；Rc1和Rc2为等效换相电阻，可用来解释换相叠弧所引起的电压下降，然而它并不表示一个实际电阻，且不消耗功率，为换流器换相电抗。在直流分层接入方式下，由于回路1与2的换流器是串联的，所以流经它们的电流Id是不变的，当Pd一定时，同时Ud保证不变，则Pd1与Pd2的值取决于Ud1与Ud2的值占Ud的比例。

2 换流母线电压相互作用因子求解

2.1 扰动前后交流系统的潮流方程

当系统处于稳定运行状态时，换流母线1和2的节点处潮流方程为［11］：

其中，i=1，2；Pi和Qi分别为注入节点i的有功和无功功率；Yij=Gij+jBij为节点导纳，由于换流母线电压等级不同，通过变比为k的变压器相连，计算节点导纳时需对变压器进行Π等值。特高压直流分层接入方式下节点网络如图2所示，图中ZT为等效到低压侧的变压器阻抗。

节点1、2处导纳矩阵为：

图2 特高压直流分层接入方式下节点网络图Fig.2 Node network in UHVDC hierarchical connection mode

当系统所受扰动为换流母线2处并联电感L造成的无功扰动，电压变化量为ΔU2，由于换流母线相互作用，换流母线1处的电压变化量为ΔU1。

根据多元函数的泰勒展开式，可得到扰动后系统增量形式的潮流方程为：

其中，i=1，2；Δθ=Δθ（2）-Δθ（1），ΔU=ΔU（2）-ΔU（1），角标（1）和（2）分别表示扰动前与扰动后的状态值。则有：

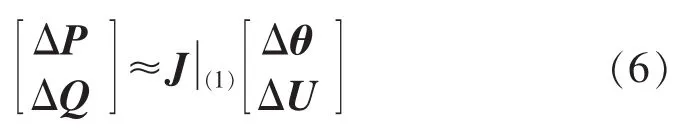
其中，为扰动前的雅可比矩阵。

根据图1所示的系统模型可知，ΔP1和ΔP2分别表示换流站和恒压源注入换流母线1和2时有功功率的变化量，ΔQ1和ΔQ2分别表示换流站和恒压源注入换流母线1和2时无功功率的变化量。

2.2 系统节点注入功率的变化量

直流输电控制方式主要有整流侧定电流控制（CCC）、逆变侧定熄弧角控制（CEC）以及整流侧CCC、逆变侧定电压控制（CVC）。因为逆变侧有2组12脉波换流器，所以在逆变侧端可以对这2组换流器进行独立控制。在整流侧CCC情况下，逆变侧有1000kV和500kV采用CEC或CVC方式和1000kV或500 kV其中一端采用CVC另一端采用CEC方式，所以在分层接入方式下直流输电共有4种控制方式。下面分析逆变侧均采用CEC或CVC方式时，换流器注入功率的变化量。

当系统采用整流侧CCC，逆变侧均采用CEC方式时，有：

当系统采用整流侧CCC，逆变侧均采用CVC方式时，有：

恒压源注入换流站有功和无功变化的变化量为：

即：

2.3 电压相互作用因子求解

本文以整流侧CCC、逆变侧CEC方式为例，则有：

假设已知换流母线2处的电压变化量ΔU2，则上式中有4个方程、8个变量，已知其中的4个变量，就可求解其余4个变量。可建立下式：

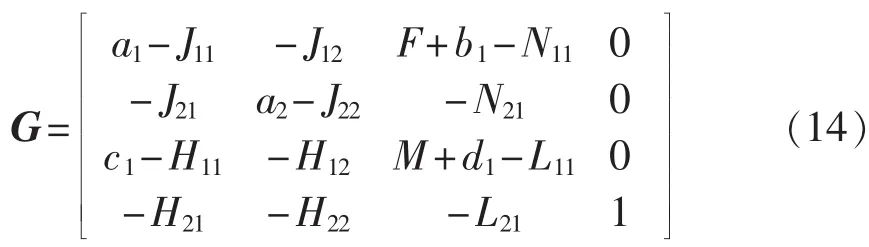
则可求解其余4个变量：

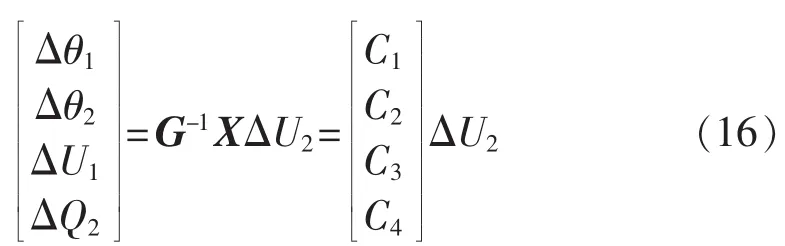
则电压相互作用因子为：

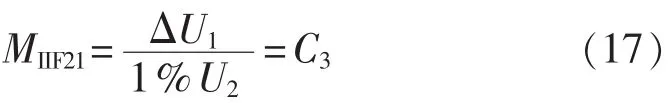
可见相互作用因子大小与投入的三相电抗器大小无关，只与交直流系统参数有关。

2.4 直流分层接入相互作用因子仿真验算

基于云广特高压系统［12-13］建立单馈入直流分层接入系统，Z1=Z2=11.416+j42.7 Ω、Z12=20+j188 Ω、θ1=0.0003 rad、θ2=0.3527 rad。 在不计及损耗的情况下，系统容量为5000 MV·A，直流电压为800 kV，换流母线1电压为1000kV，换流母线2电压为500 kV，输送到回路1与2的有功功率均为2500 MW。连接换流母线1和2的变压器容量为500 MV·A，变比为1000/525，ZT=0.18 p.u.。 系统采用整流侧 CCC、逆变侧CEC方式。

图3与图4分别为扰动前与扰动后换流母线1和母线2的电压。

图3 系统换流母线1电压Fig.3 Voltage of commutation Bus 1

图4 系统换流母线2电压Fig.4 Voltage of commutation Bus 2

由此可得出：

改变Z1、Z2的值，不改变Z12的值。对比仿真和数值计算结果，可得出推导得到的相互作用因子表达式是准确的，如表1所示。

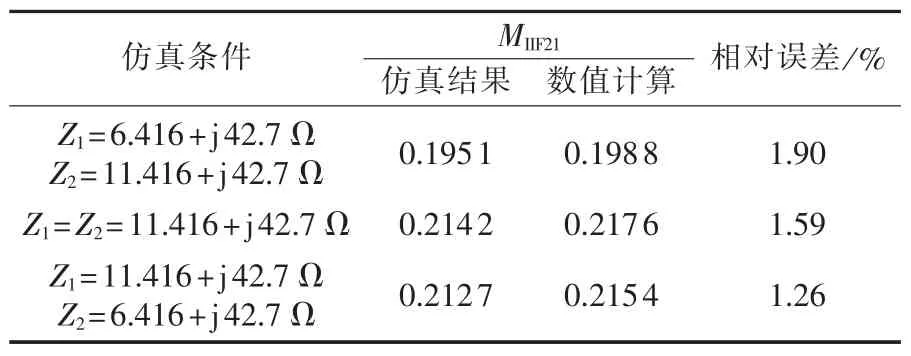
表1 MIIF21值Table1 Values of MIIF21

2.5 相互作用因子影响因素分析

2.5.1 直流落点间电气距离影响

直流分层接入换流母线间电气距离由换流母线间联系阻抗Z12来表征，Z12值大小反映换流母线间电气距离远近。图5反映出不同直流控制方式下电气距离对相互作用因子的影响，其余参数初始值均保持不变，取Z12初始值为基准值，假设等值阻抗相角不变。

由图5可以发现，随着电气距离的增大，换流母线电压相互作用因子变小，并且逆变侧均采用CVC时，相互作用因子最小。

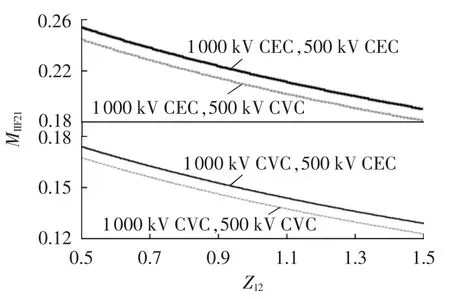
图5 不同直流控制方式下联系阻抗对系统相互作用因子的影响Fig.5 Effect of coupling impedance on MIIF for different DC control modes

2.5.2 交流系统等值阻抗的影响

图6反映出不同的直流控制方式下，交流等值阻抗改变，而其他参数未改变的情况下，系统相互作用因子的变化情况，假设等值阻抗相角不变。图6（a）中取Z1初始值为基准值，其余参数初始值均保持不变；图6（b）中取Z2初始值为基准值，其余参数初始值均保持不变。

图6 不同直流控制方式下交流系统等值阻抗对系统相互作用因子的影响Fig.6 Effect of equivalent impedance on MIIF for different DC control modes

由图 6可以发现，Z1变化对MIIF21影响较大，Z2变化对MIIF21影响较小，且逆变侧均采用CVC时，电压相互作用因子最小。

除了电气距离、交流系统等值阻抗以及直流控制方式对系统相互作用因子有影响外，直流系统结构、恒压源参数以及换流母线间变压器参数均会对相互作用因子产生影响。

3 特高压直流分层接入方式下短路比计算

短路比大小反映受端系统电压支撑能力。短路比越大说明系统对受端换流母线电压支撑能力越强。特高压直流分层接入方式下短路比MISCR（Multi-Infeed Short Circuit Ratio）计算仍然可用双馈入短路比计算公式进行计算，接入不同电压等级换流母线都需计算其短路比，即：

其中，i和j的取值为1和2，且i与j的取值不相等；Saci为回路i系统短路容量；Pdi为回路i直流额定有功功率；Pdj为回路j直流额定有功功率；Ui为换流母线i电压；Zeqii为换流母线i的自阻抗。

则在特高压直流分层接入方式下对节点1、2的导纳矩阵求逆可以得到节点阻抗矩阵为：

4 特高压直流分层接入不同受端回路对系统换相失败的影响

特高压直流分层接入能够通过独立控制各受端换流器触发角、改变变压器变比及受端交流系统参数等方式改变各交流系统输送功率的潮流分布。由式（1）和（2）可知，改变换流器熄弧角及变压器变比可使得直流有功功率功率Pd1与Pd2改变，并使得Iac1与Iac2发生变化。

而当受端回路参数变化时，Iac1与Iac2在回路1与回路2的分布会产生变化，使得Pac1与Pac2值改变，从而改变各交流系统的潮流分布。

由此可见，通过将直流功率合理分配给各换流器，能合理分配各交流系统的潮流分布。当直流输送功率Pd一定时，并保持换流母线1和换流母线2的电压值不变、变压器变比及换流器熄弧角不变时，交流回路功率Pac1与Pac2值取决于交流系统受端回路参数。通过改变受端回路参数值，可使得交流系统潮流分布发生改变。

而由前文换流母线电压相互作用因子数值计算可知，不同的受端回路参数对换流母线电压相互作用因子是有影响的，所以特高压直流分层接入不同的受端回路时，即每条回路流入的功率不同导致潮流分布发生变化时，换流母线电压相互作用因子是不一样的。

换相失败是传统高压直流输电常见的故障，而换流母线电压跌落是换相失败的主要原因。本算例以所搭建的直流分层接入系统为基础，比较接入不同受端回路的情况下，系统潮流分布发生变化时，即换流母线电压相互作用因子不同时，一条回路上发生换相失败对另一条回路的影响。

仿真中一般熄弧角小于7°时，即可判断为换流器换相失败［14-15］。故障设为换流母线1处0.8 s时发生较大无功扰动，1.2 s后扰动去除。未改变交流系统参数时，MIIF12=0.1608，换流母线电压相互作用因子较小。图7为这种情况下的交流回路功率，其中Pac1约为2 900 MW，Pac2约为2 000 MW。如图8所示，回路1换流器发生换相失败时，由于换流母线1电压下降，导致直流电流突然增大，回路2的换流器短时间发生换相失败，继而换相能力恢复，图中γ1与γ2分别表示换流器1与换流器2的熄弧角。

图7 交流回路功率Fig.7 Active power of AC circuit

图8 系统直流电流和熄弧角仿真图Fig.8 Simulative waveforms of DC current and arc extinguish angle

改变交流系统结构参数，测得此时的MIIF12=0.4533，图9为这种情况下的交流回路功率，其中Pac1约为3300 MW、Pac2约为1600 MW。如图10所示，回路1换流器发生换相失败会导致回路2换流器也会发生换相失败。

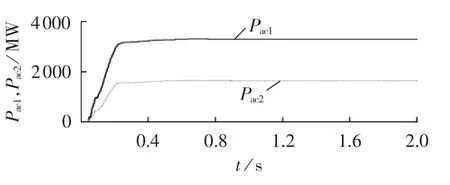
图9 交流回路功率Fig.9 Active power of AC circuit

图10 系统熄弧角仿真图Fig.10 Simulative waveform of arc extinguish angle

由以上分析可知，在特高压直流分层接入不同的受端系统，保持输送直流功率不变，换流母线间的电压相互作用因子较大时，若一条回路上换流器发生换相失败，则会增加另一回路也发生换相失败的风险。

5 结语

本文提出了特高压直流在分层接入方式下，换流母线电压相互作用因子的求解方法，并用仿真进行验证，对其影响因素进行了分析。根据所求的相互作用因子，可得到分层接入时系统短路比。直流分层接入不同受端系统时能够使得潮流重新分布，但会对系统换流母线电压相互作用因子、系统短路比以及换相失败风险产生影响。

［1］刘振亚，秦晓辉，赵良，等.特高压直流分层接入方式在多馈入直流电网的应用研究［J］.中国电机工程学报，2013，33（10）：1-7.LIU Zhenya，QIN Xiaohui，ZHAO Liang，et al.Study on the application of UHVDC hierarchical connection mode to multi-infeed HVDC system［J］.Proceedings of the CSEE，2013，33（10）：1-7.

［2］肖俊，李兴源.多馈入和多端交直流系统相互作用因子及其影响因素分析［J］.电网技术，2014，38（1）：1-7.XIAO Jun，LI Xingyuan.Analysis on multi-infeed interaction factor of multi-infeed AC/DC system and multi-terminal AC/DC system and its influencing factor［J］.Power System Technology，2014，38（1）：1-7.

［3］陈修宇，韩明晓，刘崇如.直流控制方式对多馈入交直流系统电压相互作用的影响［J］.电力系统自动化，2012，36（2）：58-63.CHEN Xiuyu，HAN Mingxiao，LIU Chongru.Impact of control modes on voltage interaction between multifeed AC-DC system［J］.Automation of Electric Power Systems，2012，36（2）：58-63.

［4］申洪明，黄少锋，费彬.HVDC换相失败暂态特性及其对差动保护的影响分析和对策［J］.电力自动化设备，2015，35（4）：109-120.SHEN Hongming，HUANG Shaofeng，FEI Bin.The transient characteristics of HVDC commutation failure and its impact analysis and countermeasures on differential protection［J］.Electric Power Automation Equipment，2015，35（4）：109-120.

［5］杨鹏，吴娅妮，马士聪，等.±1100 kV特高压直流输电工程直流线路故障重启动过程非故障极换相失败研究［J］.电力自动化设备，2016，36（4）：14-18.YANG Peng，WU Yani，MA Shicong，et al.Study on non-fault phase commutation failure in±1100 kV UHVDC transmission line fault restart process［J］.Electric Power Automation Equipment，2016，36（4）：14-18.

［6］邵瑶，汤涌.多馈入直流系统交互作用因子的影响因素分析［J］.电网技术，2013，37（3）：794-799.SHAO Yao，TANG Yong.Analysis of influencing factors of multiinfeed HVDC system interaction factor［J］.Power System Technology，2013，37（3）：794-799.

［7］刘健，李兴源，傅孝韬，等.多馈入短路比及多馈入交互作用因子与换相失败的关系［J］.电网技术，2009，33（12）：20-25.LIU Jian，LI Xingyuan，FU Xiaotao，et al.Relationship of multiinfeed short ciruit ratio and multi-infeed interaction factor with commutation failure［J］.Power System Technology，2009，33（12）：20-25.

［8］李妮，李兴源，冯明，等.改善多馈入直流系统电压无功特性的直流控制策略［J］.电力自动化设备，2016，36（2）：25-31.LI Ni，LI Xingyuan，FENG Ming，et al.Direct current control strategy to improve the reactive power characteristics of multiinfeed DC system voltage［J］.Electric Power Automation Equipment，2016，36（2）：25-31.

［9］郭小江，汤涌，郭强，等.CIGRE多馈入直流短路比指标影响因素及机理［J］.电力系统保护与控制，2012，40（9）：69-74.GUO Xiaojiang，TANG Yong，GUO Qiang，et al.Influence factors and theory for CIGRE MISCR index［J］.Power System Protection and Control，2012，40（9）：69-74.

［10］林伟芳，汤涌，卜广全.多馈入交直流系统短路比的定义和应用［J］.中国电机工程学报，2008，28（31）：1-8.LIN Weifang，TANG Yong，BU Guangquan.Definition and application of short cicuit ratio for multi-infeed AC/DC power system［J］.Proceedings of the CSEE，2008，28（31）：1-8.

［11］高媛，韩民晓.特高压直流输电多端馈入方式稳态特性研究［J］.电网技术，2014，38（12）：3447-3452.GAO Yuan，HAN Minxiao.Steady state characterisitic of multiinfeed UHVDC power transmission［J］.Power System Technology，2014，38（12）：3447-3452.

［12］陈仕龙，束洪春，叶波，等.云广±800 kV特高压直流输电系统精确建模及仿真［J］.昆明理工大学学报（自然科学版），2012，37（2）：43-48.CHEN Shilong，SHU Hongchun，YE Bo，et al.Accurate modeling and simulation of Yun-Guang UHVDC transmission system ［J］.Journal of Kunming University of Science and Technology（Natural Science Edition），2012，37（2）：43-48.

［13］许爱东，柳勇军，吴小辰.±800 kV云广特高压直流安全稳定控制策略研究［J］.南方电网技术，2008，2（5）：14-18.XU Aidong，LIU Yongjun，WU Xiaochen.Study on security and stability control for±800 kV Yun-Guang UHVDC transmission［J］.Southern Power System Technology，2008，2（5）：14-18.

［14］李兴源.高压直流输电系统［M］.北京：科学出版社，2010：99-120.

［15］袁阳，卫志农，雷霄，等.直流输电系统换相失败研究综述［J］.电力自动化设备，2013，33（11）：140-147.YUAN Yang，WEI Zhinong，LEI Xiao，et al.Research survey on commutation failure in DC transmission system［J］.Electric Power Automation Equipment，2013，33（11）：140-147.Steady-state characteristics of UHVDC hierarchical connection mode