基于动态规划算法的配电网孤岛划分策略

李红伟 ，林山峰 ，吴华兵 ，张安安

（1.西南石油大学 电气信息学院，四川 成都 610500；2.国家电网乐山供电公司，四川 乐山 614000）

0 引言

配电网故障的不可预测性使重要负荷的供电连续性得不到保障，分布式电源（DG）的接入则有效缓解了这一问题，提高了配电网供电的可靠性和灵活性［1-4］。但DG的接入也给配电网的运行和控制带来了许多负面影响［5-7］。为使DG能够在配电网中充分发挥积极作用，IEEE提出了新的标准，鼓励有意识的孤岛运行［8-9］。所谓孤岛，即配电系统的部分用户仅由DG进行供电，包含这部分用户以及DG的系统［9］。

近年来，国内外诸多专家和学者对配电网孤岛的划分策略进行了深入的研究。文献［8］提出一种基于Kruskal算法的分布式孤岛划分方法，把孤岛划分问题转化为求连通图的最小生成树问题，并利用改进的Kruskal算法制定搜索规则，确定最优孤岛划分范围，采用了边搜索边校验的方法保证了孤岛的正常运行。文献［10］提出了一种基于树背包问题的含分布式发电配电系统最优孤岛划分新模型；在孤岛形成过程中全面考虑了负荷等级和可控性等因素，其算法具有恢复负荷多、孤岛网损小等优点，该算法形成的孤岛在考虑负荷可控性和负荷等级的基础上还可以继续优化。文献［11］利用配电网辐射状的特点对配电网的层次进行了划分，最终目的都是降低孤岛搜索的复杂度，但没有考虑实际电网中负荷是否可控的情况。文献［12］主要是根据孤岛运行时的功率平衡要求进行孤岛划分，采用启发式的搜索策略实现，但并未区分负荷的重要等级。文献［13］以孤岛内功率平衡条件为约束，利用图论分析法中的Sollin算法求解最小树，进而实现孤岛的划分。文献［14］采用启发式搜索策略及广度优先搜索算法兼顾不同类型的DG特点，提出配电网计划孤岛划分组合算法。文献［15］在整个失电区域内形成一个孤岛，保证了优先级较高的负荷供电的可靠性，但孤岛的规模大，孤岛网损较大。文献［16］针对含微电网的配电网发生故障后恢复供电的孤岛划分问题，提出考虑了微电网内间歇性电源与负荷随机性的微电网供电潜力的配电网多目标孤岛划分优化模型。

孤岛的划分就是确定各节点是否应该纳入孤岛使得产生的总收益最大，实质上是一个0-1整数规划问题，利用动态规划算法可以快速对其求解。但其解并不能作为最终的孤岛形成方案，实际配电网中还有负荷优先级和可控性以及系统潮流、节点电压、线路载流等约束，所以应不断修正孤岛来形成最优孤岛。本文所提方法的优点是在初级孤岛修正形成次级孤岛时，考虑了孤岛外边缘可控负荷的优先等级和负荷量，将优先级高的可控负荷部分替换孤岛内优先级低的可控负荷或全部替换孤岛内边缘处负荷，从而使孤岛进一步优化。

1 初级孤岛形成方案

1.1 DG最大供电范围的确定

为了减少DG的接入给配电网带来的不利影响，实际中接入配电网的DG功率一般较小；作用是在发生故障时为其周边负荷提供持续的电力供应，失电区内的负荷不可能都依靠其恢复供电，所以根据DG的容量确定孤岛形成的最大范围，把超出DG供电范围的负荷剔除掉，这样可以减少计算量，提高算法的效率。

DG的最大供电范围（用Dmax表示，下同）为从DG出发，沿着每条无分支路径（供电路径上不存在分支支路）在DG容量约束下所能包含的负荷组成的连通区域；以DG为根结点进行深度优先搜索，边搜索边检查DG的容量约束。以图1（图中各节点负荷量及DG最大发电量均标示在节点左侧，单位kW，负荷全部为不可控负荷）所示的失电区域为例，当沿路径DG-0-5-6搜索至节点7时，由于加入节点7后负荷需求功率已经超出DG的最大出力，故搜索节点8；加入节点8后仍然满足DG容量约束，故无分支路径DG-0-5-6-8确定。其他支路依此类推，最终确定Dmax为图1中以实线连通的区域。

图1 含DG的连通区域Fig.1 Connected areas including DG

1.2 孤岛划分建模及动态规划算法

确定Dmax后，当该范围内的负荷不能全部恢复供电，选择恢复部分负荷使得产生的效益最大，即目标函数值最大；目标函数综合考虑了总恢复负荷量和负荷优先级。

其中，i为 Dmax中的负荷节点，即 iєDmax，i=1，2，…，n，n为失电区总负荷节点数；j为负荷节点i与发电机节点连通路径上的负荷节点；xi为标示节点i是否包含于孤岛内，xi=0表示负荷i在孤岛外，xi=1表示负荷 i在孤岛内，xk、xj的含义同理；ωi为节点 i的负荷量；vi为节点 i的权值量，vi=riωi，ri为负荷 i的等级系数，Ⅰ、Ⅱ、Ⅲ级负荷 ri分别取 100、10、1；k 为 Dmax中的发电机节点；Gk为发电机k的最大出力。

式（2）为功率约束，表示孤岛内负荷总量不得超过发电机的最大有功输出；式（3）表示发电机节点作为根结点必然会包含在孤岛内；式（4）表示任一负荷节点要么包含于孤岛内，要么处于孤岛外；式（5）为孤岛连通约束，表示若节点i包含于孤岛内，则该节点与发电机连通路径上的所有负荷节点也应该包含于孤岛内。

根据动态规划算法的最优性理论，一个最优化策略具有这样的性质：不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略［17］。初级的形成包含求解最优值和确定构成最优值的节点组合2步，求解最优值采用的是逐个求解节点i对应的目标函数值，而节点i的目标函数值是在前i-1个节点的目标函数值基础上求得，所以对于节点n，初级孤岛问题的子问题为第i个节点对应目标函数值，当i=n时即可确定初级孤岛最优值。

式（6）、（7）的最优解为 f（i，gk），其中 gkє［0，Gk］，且 gk为整数，f（i，gk）表示当第 k 个 DG 出力为 gk时，孤岛包含负荷i、i+1、…、n时的最优解。由最优性理论可以建立计算 f（i，gk）的递推公式为：

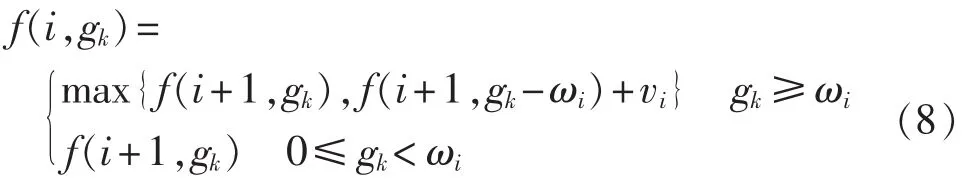
初始条件：

基于上述递推式（8）和初始条件式（9）可以求出初级孤岛包含的负荷以及目标函数的最大值，根据最大值可确定初级孤岛包含的节点。

需要注意的是，所有负荷均视为不可控负荷，若要考虑负荷的可控性则算法复杂度将大幅增加，此问题将在孤岛修正时讨论；算法中涉及的负荷量和发电机出力均为整数，而实际中并不为整数，因此采用kW为单位，对ωi取下整数，而Gk取上整数，之所以这样取值是考虑到孤岛内还存在一定网损；如果由各DG确定的孤岛之间有公共节点，为了减少开关操作而形成组合孤岛，组合孤岛的出力为各DG出力之和。配电网一般具有良好的就地无功补偿能力，无功功率不会远距离传输。针对孤岛内的DG，假定其具有良好的无功补偿能力，并且其无功补偿只考虑DG近处负荷的需求，而各远处负荷都具有较好的无功补偿能力。所以，无功功率对DG的有功输出影响很小，因此，在孤岛划分时仅需要考虑孤岛内的有功功率平衡。

2 初级孤岛修正形成次级孤岛

初级孤岛形成后，岛内边界（定义为岛内每条无分支路径的非DG端点构成的边界，如图1中的节点 2、4、8、10）和岛外边界（定义为孤岛外原先与孤岛内节点相连的节点所构成的边界，如图1中的节点7和11）可控负荷的存在使得初级孤岛结构可能并不是最优；根本原因在于孤岛连通约束的存在。仍以图1为例来简单说明，假设岛内节点10为100%可控负荷，并且其优先级低于节点11，则切除节点10上的9 kW负荷同时把节点11纳入孤岛，这样做不但没有违背上述4个约束条件，反而增加了目标函数值，孤岛方案因此得到了优化。

初级孤岛能否优化关键在于岛内或岛外边界是否有可控负荷存在，且和可控负荷的大小和等级有关。首先搜索岛外边界上是否存在可控负荷，这是因为实际工程中DG的最大有功输出往往大于岛内总功率需求，即DG出现功率剩余，此时可以通过接入岛外边界上的可控负荷来减少DG的功率剩余。再次搜索岛内可控负荷和岛外边界上的剩余可控负荷，其分布包括以下3种情况。

（1）全部分布在孤岛内。

设孤岛内的可控负荷数量和孤岛外边界上的不可控负荷数量分别为x和y，对于孤岛内可控负荷p=1，2，…，x，以及孤岛外边缘不可控负荷 q=1，2，…，y，孤岛的修正步骤如下。

a.初始化，p=1，q=1，qmin=q。

b.若p≤n则转步骤c；否则算法结束。

c.若 q≤m 则转步骤 d；否则 q=qmin，p=p+1，转步骤b。

d.判断p、q是否满足式（10），若满足则切除p上的 ωq（kW）负荷并接入负荷 q，ωp=ωp-ωq，qmin=q+1，转步骤e；否则直接转步骤e。

其中，上标“in”表示孤岛内边界；上标“out”表示孤岛外边界。

e.q=q+1；转步骤 c。

上述步骤中qmin表示孤岛外边界上编号最小的点。当负荷p位于孤岛内边缘时，式（10）的第二个约束还可以拓宽至图2表示孤岛的修正过程（其中p、q表示负荷节点；Ⅰ、Ⅱ、Ⅲ表示负荷等级；括号中数字表示负荷量，单位kW；C、U分别表示负荷可控和不可控）。

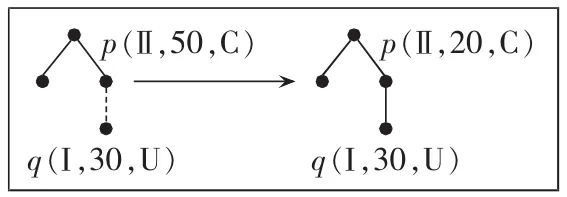
图2 可控负荷位于孤岛内时孤岛的修正Fig.2 Modification of islanding scheme when all controllable loads are included

（2）全部分布在孤岛外边缘。

设孤岛内边界的不可控负荷数量和孤岛外边界上可控负荷数量分别为x和y，对于孤岛外边缘上可控负荷q=1，2，…，y，以及孤岛内边界上的不可控负荷 p=1，2，…，x，孤岛的修正步骤如下。

a.初始化，p=1，q=1，pmin=p。

b.若q≤m则转步骤c；否则算法结束。

c.判断p是否与q相邻，若相邻，则p=p+1；否则转步骤d。

d.若 p≤n 则转步骤 e；否则 p=pmin，q=q+1，转步骤b。

e.判断 p、q是否满足式（11），若满足则切除负荷 p，接入负荷 q，ωq=ωq-ωp，pmin=p+1，转步骤 f；否则直接转步骤f。

f.p=p+1；转步骤 d。

图3表示孤岛的修正过程（其中q1、q2表示负荷节点），修正后孤岛内又增加了可控负荷，转化为情况（1）。

图3 可控负荷位于孤岛外时孤岛的修正Fig.3 Modification of islanding scheme when all controllable loads are not included

（3）孤岛内和孤岛外边缘均有分布。

此种情况下孤岛的修改可以先后视为上述2种情况进行讨论。但又由于孤岛内外同时存在可控负荷这一特殊性，使得原先的修改方案需要添加一定的修正规则。

a.按照情况（1）来讨论时，对于孤岛内可控负荷p，搜索岛外边缘负荷等级高于rp的可控负荷和负荷量小于ωp的不可控负荷。当2类负荷同时存在时优先把不可控负荷纳入孤岛；若只有不可控负荷存在，则在孤岛连通约束下尽可能多地切除可控负荷，将岛外负荷纳入孤岛，形成新的孤岛边界。该孤岛过程可用图4来表示（其中i表示负荷节点）。

图4 孤岛内外均有可控负荷时孤岛的修正（情况a）Fig.4 Modification of islanding scheme when some controllable loads are included and some not （Case a）

b.当经过步骤a修正后岛外边缘还有可控负荷存在时，按照情况（2）来讨论。对于岛外边缘可控负荷q，搜索岛内边缘负荷等级低于rq与q不相邻且负荷量小于ωq的不可控负荷以及岛内负荷等级低于rq的全部可控负荷。优先切除岛内边缘不可控负荷同时加入负荷q；然后在孤岛连通约束下尽可能多地切除岛内可控负荷，形成新的孤岛边界。其孤岛修正过程如图5所示。

图5 孤岛内外均有可控负荷时孤岛的修正（情况b）Fig.5 Modification of islanding scheme when some controllable loads are included and some not （Case b）

每当有新的孤岛边界形成时，重复上述算法，按照规则对孤岛进行修正，直到孤岛边界不能再修正为止。至此，形成次级孤岛。

3 次级孤岛可行性校验

由于初级和次级孤岛的生成过程中均未考虑孤岛内的线路损耗和电压约束，所以孤岛能否稳定运行还有待检验；当负荷总量等于DG最大出力时，计及孤岛内的线路损耗后总功率损耗将会超出DG的最大出力，这将导致孤岛无法稳定运行，应切除部分低级负荷。

对孤岛进行潮流计算时，单DG孤岛中将发电机节点作为平衡节点，多DG孤岛中将出力最大的节点作为平衡节点，而其他节点作为PV节点［10］。若孤岛内出现节点电压越限，则采取启动无功补偿装置等手段来保证节点电压处于正常范围内；如出现线路过载，则适当切除线路上的负荷；校验后可以稳定运行的孤岛作为最终的孤岛方案。

4 算例及对比分析

本文采用IEEE 69节点系统（如图6所示）来测试本文所提孤岛形成策略。IEEE 69节点系统中各母线负荷及线路的参数详见文献［18］。DG1—DG4分别通过母线6、10、24、53接入系统，其最大输出有功功率分别为 200 kW、400 kW、230 kW、350 kW。节点 6、12、18、24、40、42、53、57 所接负荷为Ⅰ类负荷；节点 8、9、13、16、17、26、37、41、44、50、55、56、58所接负荷为Ⅱ类负荷；其余节点所接负荷均为Ⅲ类负荷。节点 9、11、12、17、21、26、41、50 所连负荷为100%可控负荷，其余节点所带负荷均为不可控负荷。

假设母线3和母线4之间发生故障，运用本文的算法，孤岛形成过程如下。由动态规划算法确定的初级孤岛分别为：孤岛 1，｛DG1，DG2，6—13，40—42，55，57，58｝；孤岛 2，｛DG3，18 — 26｝；孤岛 3，｛DG4，51—54｝。初级孤岛如图6所示，岛内有功剩余分别为3.55 kW、7.7 kW、32 kW。孤岛1外边界上无可控负荷存在，而岛内存在Ⅲ类可控负荷11，岛外边界上存在满足式（10）的节点56和节点37，故切除节点11上97 kW负荷，把节点56和37划入孤岛，形成新的孤岛。经检验，新的孤岛无法继续修正，此孤岛即为次级孤岛。对于孤岛2的修正，首先接入节点 17上的7.7 kW负荷使DG3的剩余容量为0，此时孤岛内外均存在可控负荷，按照修正规则，首先切除节点21上52.3kW负荷，接入节点17上的剩余负荷，修正后的新孤岛外边缘上已无可控负荷存在，但对于岛内可控负荷21，存在岛外负荷节点16满足式（10），因此切除节点21上52.3 kW负荷，把节点16融入孤岛，至此，次级孤岛形成。孤岛3的修正同理，修正后的孤岛 3 为｛50（91 kW）—53，DG4｝。

修正后的次级孤岛的DG剩余容量分别为3.55 kW、0、0。分别对3个孤岛进行可行性校验，网损分别为3.71 kW、0.27 kW、0.02 kW，因此分别切除节点 11、21、50上的 0.5 kW、0.3 kW、0.1 kW 负荷，再次计算，孤岛内总负荷加网损均未超过DG的最大出力，另外，各节点电压均未越限，并且岛内各条线路均未过载，孤岛可以稳定运行。最终的孤岛方案如图6所示（图中较细的母线表示其上负荷被部分切除）。恢复负荷总量为1175 kW。

在本算例中分别用文献［10］和［12］中所提孤岛划分算法进行孤岛划分，得到的孤岛方案如图7所示。文献［10］算法求得的孤岛中节点17和节点50上被切除52 kW负荷；文献［12］算法求得的孤岛中节点12和节点50上分别被切除29.25 kW和91 kW负荷。恢复负荷总量分别为1175 kW和1126.3 kW。文献［10］中算法虽然与本文算法恢复负荷量之和相同，且Ⅰ类负荷均全部恢复，但本文孤岛中包含的Ⅱ类负荷比例为39.7%，高于文献［10］的23.3%，原因在于当孤岛内和孤岛外同时存在满足式（10）的负荷时，较低级负荷可被较高级负荷替代，且由此带来的网损可以忽略不计。而文献［10］中并没有孤岛修正措施，不能融入更多的Ⅱ类负荷。

图6 IEEE 69节点系统Fig.6 IEEE 69-bus system

图7 文献［10］和［12］算法求得的孤岛Fig.7 Islanding schemes by reference ［10］and ［12］

文献［12］算法之所以比本文算法恢复负荷少是因为其在融合负荷节点时若遇到负荷量较大的不可控负荷，在DG剩余容量充裕的情况下可以将其融入孤岛，但如果DG剩余容量不足则融合过程终止，这就造成了DG的出力未被充分利用，其DG利用率为95.4%，而本文DG的利用率达到了99.6%。另外，文献［12］在孤岛范围扩充时若岛外边界上全是低级负荷，则只有将其融合，若之后遇到较高等级负荷（可控）只能将其部分融入（如Ⅰ类节点12上被切除的29.25 kW负荷），这就造成了较高等级负荷的恢复得不到保障，而本文恢复了所有的Ⅰ类负荷。

上述的对比表明，本文的孤岛生成算法相对于其他文献中的算法具有优越性。

5 结论

本文提出一种基于动态规划算法的孤岛划分方法，在生成初级孤岛时不考虑负荷的可控性，简化了动态规划算法的计算过程，节省了计算时间，在一定程度上提高了算法效率；制定一系列的细致的孤岛修正方案对孤岛进行修正，修正后的孤岛能够恢复更多的负荷；最终对孤岛的可行性进行校验，保证了孤岛的稳定运行；算例分析验证了本文所提算法的可行性，同时与其他算法的对比验证了该算法的优越性。

［1］孙洁，王增平，王英男，等.含分布式电源的复杂配电网故障恢复［J］.电力系统保护与控制，2014，42（2）：56-62.SUN Jie，WANG Zengping，WANG Yingnan，et al.Service restoration of complex distribution system with distributed generation［J］.Power System Protection and Control，2014，42（2）：56-62.

［2］王昌照.含分布式电源配电网故障恢复与可靠性评估研究［D］.广州：华南理工大学，2015.WANG Changzhao.Research on service restoration and reliability evaluation of distribution network with distributed generation［D］.Guangzhou：South China University of Technology，2015.

［3］赵晶晶，杨秀，符杨.考虑分布式发电孤岛运行方式的智能配电网供电恢复策略研究［J］.电力系统保护与控制，2011，39（17）：45-49.ZHAO Jingjing，YANG Xiu，FU Yang.Smart distribution system service restoration using distributed generation islanding technique［J］.Power System Protection and Control，2011，39（17）：45-49.

［4］王旭斌，李鹏，窦鹏冲，等.用于微网孤岛运行的新型功率控制方法［J］.电力自动化设备，2014，34（6）：122-134.WANG Xubin，LI Peng，DOU Pengchong，et al.Power control method for autonomous microgrid［J］.Electric Power Automation Equipment，2014，34（6）：122-134.

［5］张超，计建仁，夏翔，等.分布式发电对配电网继电保护及自动化的影响［J］.华东电力，2006，34（9）：23-26.ZHANG Chao，JI Jianren，XIA Xiang，et al.Effect of distributed generation on relay protection and automation of distribution network［J］.East China Electric Power，2006，34（9）：23-26.

［6］张立梅，唐巍，赵云军，等.分布式发电对配电网影响的综合评估［J］.电力系统保护与控制，2010，38（21）：132-135，140.ZHANG Limei，TANG Wei，ZHAO Yunjun，et al.The integrated evaluation of impact of distributed generation on distribution network［J］.Power System Protection and Control，2010，38（21）：132-135，140.

［7］刘锐，刘敏，辜俊明.浅析分布式电源接入对配电网的影响［J］.机械工程与自动化，2013（3）：220-222.LIU Rui，LIU Min，GU Junming.Impacts of distributed generation on distribution network ［J］.Mechanical Engineering Automation，2013（3）：220-222.

［8］刘宗歧，鲍巧敏，孙春山，等.基于改进Kruskal算法的含分布式发电的配网孤岛划分算法［J］.电工技术学报，2013，28（9）：164-171.LIU Zongqi，BAO Qiaomin，SUN Chunshan，et al.Islanding algorithm of distribution system with distributed generations based on improved Kruskal alogorithm［J］.Transactions of China Electrotechnical Society，2013，28（9）：164-171.

［9］IEEE.IEEE standard for interconnection distributed resources with electric power system：IEEE Std 1547［S］.Iscataway，NJ，USA：IEEE，2003.

［10］王旭东，林济铿.含分布发电配电系统的孤岛划分［J］.中国科学：技术科学，2011，41（5）：693-702.WANG Xudong，LIN Jikeng.Island partition of the distribution system with distributed generation ［J］.Scientia Sinica Technologica，2011，41（5）：693-702.

［11］丁磊，潘贞存，丛伟.基于有根树的分布式发电孤岛搜索［J］.中国电机工程学报，2008，28（25）：62-67.DING Lei，PAN Zhencun，CONG Wei.Searching for international islanding strategy of distributed generation based on rooted tree［J］.Proceedings of the CSEE，2008，28（25）：62-67.

［12］易新，陆于平.分布式发电条件下的配电网孤岛划分算法［J］.电网技术，2006，30（7）：50-54.YI Xin，LU Yuping.Islanding algorithm of distribution networks with distributed generators［J］.Power System Technology，2006，30（7）：50-54.

［13］曾令诚，吕林，曾澜钰.基于Sollin算法的含分布式电源的孤岛划分方法［J］.电力自动化设备，2013，33（4）：95-100.ZENG Lingcheng，LU¨Lin，ZENG Lanyu.Islanding method based on Sollin algorithm for grid with distributed generations［J］.Electric Power Automation Equipment，2013，33（4）：95-100.

［14］党克，张慧明，朱景明，等.配电网计划孤岛划分方法研究［J］.中国电力，2010，43（9）：66-70.DANG Ke，ZHANG Huiming，ZHU Jingming，et al.Research of planned island grouping operation of distribution system ［J］.Electric Power，2010，43（9）：66-70.

［15］MAO Yiming，MIU K N.Switch placement to improve system reliability for radial distribution systems with distributed generation［J］.IEEE Transactions on Power Systems，2003，18（4）：1346-1352.

［16］张晓雪，牛焕娜，赵静翔，等.考虑微电网供电潜力的配电网孤岛划分［J］.电力自动化设备，2016，36（11）：51-58.ZHANG Xiaoxue，NIU Huanna，ZHAO Jingxiang，et al.Distribution network island partition considering potential power-supply of microgrid［J］.Electric Power Automation Equipment，2016，36（11）：51-58.

［17］滕宇，梁方楚.动态规划原理及应用［M］.成都：西南交通大学出版社，2011.

［18］CALDON R，STOCCO A，TURRI R.Feasible of adaptive intentional islanding operation of electric utility systems with distributed generation［J］.Electric Power Systems Research，2008，78（12）：2017-2023.