基于功率矩和邻域搜索的有源配电网两层重构算法

吉兴全，刘 琪，于永进

（山东科技大学 电气与自动化工程学院,山东 青岛 266590）

0 引言

配电网络重构是配电系统自动化的重要功能模块之一，按应用场景的不同，配电网重构可分为正常运行状态下的重构和事故后的重构2种类型。前者通常以降低网络损耗、提高电压水平、平衡负荷等为目标，通过配电开关状态的组合寻求最佳的网络拓扑结构；后者又称为故障恢复，往往以负荷恢复量最大、用户停电时间最短等为优化目标，也是通过开关状态的最优组合尽可能多地将停电区域的负荷转供到正常的馈线上。本文仅对前者进行研究。

配电网重构问题本质上属于非线性组合优化问题，难以获得精确解，而且随着研究系统规模的增大，解空间呈指数规律增长。随着智能电网的发展，越来越多的分布式电源DG（Distributed Generation）接入配电网，增加了配电网重构的复杂性。目前针对配电网络的重构问题，国内外学者提出了多种解算方法。考虑重构模型中控制变量的整数特征，文献［1］首先提出了一种基于分支定界法的重构算法，但由于需要对每个节点进行计算，当系统节点数量较多时，该方法计算效率不高。文献［2］提出的支路交换法则是基于启发式规则，以开关状态变化所引起的网损变化量为依据，将网损下降最多的开关与联络开关进行状态交换，通过逐步迭代获取最终的重构方案，降低了计算复杂度。文献［3］在文献［2］的基础上进行了改进，通过计算各联络开关所在环路的最佳转移负荷，确定降损最多的开关，提高了寻优效率，但此类算法由于搜索范围有限，最终解的质量往往不够高。由于启发式算法的全局搜索性能较差，遗传算法［4］、禁忌搜索算法［5］、协同进化算法［6］、差分进化算法［7］等智能优化算法被应用到配电网重构问题的求解中。文献［8-9］则将配电网划分为若干环路，每个环路对应一个优化变量，采用模拟植物生长算法进行配电网重构。对于含有DG的配电网重构目前主要采用智能优化算法。文献［10］采用恒功率模型，将DG视为并网节点上的功率值为负的负荷，采用改进的遗传算法对含DG的配电网进行重构。文献［11］将开关状态和DG出力同时作为优化变量，利用蛙跳算法进行全局寻优，以实现配电网的优化运行。文献［12］采用改进遗传算法对含有DG和静止无功补偿器的配电网进行重构优化。智能优化算法应用到含有DG的配电网重构中具有较强的全局搜索能力，且通常具有隐含并行性，但普遍存在计算量较大、计算时间长的不足，极大地限制了其工程应用价值。

为了解决启发式算法难以获取令人满意的重构方案，而智能优化算法计算时间较长的问题，本文提出基于功率矩和邻域搜索的配电网两层重构优化算法，首先通过功率矩算法进行配电网第一层重构，确定各环路的断开开关集，在此基础上采用具有方向的邻域搜索算法进行第二层优化重构，获取使网络损耗进一步降低的重构方案。

1 配电网重构的数学模型

本文将网络损耗最小作为配电网重构的优化目标：

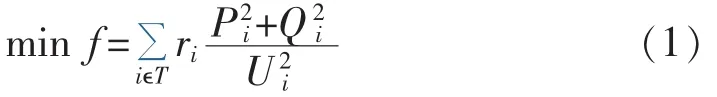
其中，Pi和Qi分别为支路末端的有功功率和无功功率；ri为支路i的电阻；Ui为支路i末端节点的电压幅值；T为配电网的支路集合。

由于DG准入容量的限制［13］以及功率矩算法只是作为配电网优化重构的初步结果，因此在基于功率矩的第一次重构优化中将DG模型视为恒功率模型，DG视为并网节点上功率值为负的负荷，在利用邻域搜索算法进行第二层优化重构时再根据DG的具体形式采用对应的节点类型［14］，通过精确的潮流计算得到重构的最终结果。

网络重构需要满足下列约束条件。

（1）配电网络辐射状运行条件约束，网络中无环路和孤立节点。

（2）电压约束：

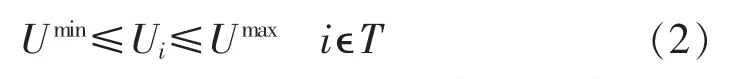
其中，Umax和Umin分别为节点电压的上限和下限。

（3）支路容量约束：

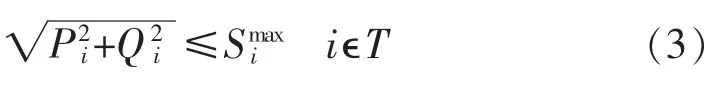
其中为支路i的最大允许功率。

（4）DG 出力约束：

其中，PG，k和 QG，k分别为 DG k 输出的有功功率和无功功率和分别为 DG k 的有功和无功功率上限值。

2 基于功率矩算法的第一层优化重构

2.1 功率矩算法

相关研究表明，采用支路交换法进行配电网重构时，将环路中功率矩不平衡度最小的支路作为被断开的支路时网络损耗最小［15］。与功率矩算法相关的几个概念定义如下。

（1）逆流路径。节点i的逆流路径Li定义为从节点i到所在环路的功率流入点所经历的支路和节点集合。

（2）阻抗距离。节点i的阻抗距离Zi为其逆流路径Li上的所有支路阻抗之和。

（3）广义负荷。节点i的广义负荷Wi为节点i到所在环路功率流入点的阻抗距离Zi与该节点负荷复功率共轭值S*i的乘积。若节点i接有DG，则将其输出功率视为负的负荷功率进行等值处理。

（4）功率矩。节点i的功率矩Ti为其逆流路径Li上所有节点的广义负荷之和的实部。

（5）功率矩不平衡度。支路b两端节点i和j的功率矩不平衡度ΔTb定义为节点i和节点j功率矩之差的绝对值，即

以图1所示的IEEE 33节点配电系统［16］为例，当所有联络开关断开、分段开关闭合时，节点25的逆流路径表示为 L25=｛25，B24，24，B23，23，B22｝；阻抗距离为Z25=ZB24+ZB23+ZB22；广义负荷为W25=Z25S*25；功率矩为 T25=Re（W25+W24+W23）；支路 B37两端节点的功率矩不平衡度为

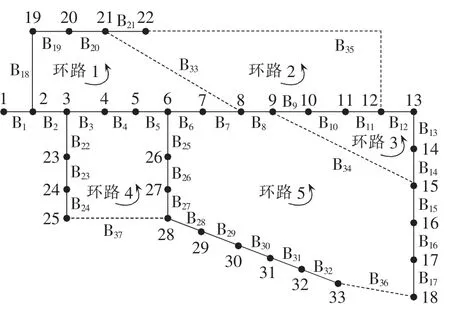
图1 IEEE 33节点配电系统Fig.1 IEEE 33-bus distribution system

传统的功率矩算法［15］是先将功率矩不平衡度最大的联络开关闭合，再在该联络开关所在的环路中寻找功率矩不平衡度最小的开关将其断开，直至对其余所有联络开关完成上述操作。

事实上，对于某一具体的联络开关及其所在的环路，只有当其他环路的开关状态保持不变时，通过经典的功率矩算法得到的该环路的开关状态组合才可使整个网络的损耗降低，显然随着对其他环路中联络开关的处理，这一条件会遭到破坏。换言之，由于经典的功率矩算法并未考虑迭代过程中环网之间的相互影响，因此最终解的质量往往不高。但另一方面，功率矩算法具有无需潮流计算、单步优化计算量很小的突出优点，而且对每一个迭代步，功率矩算法的优化方向与系统的有功网损下降方向具有显著的对应关系［15］。为此，本文首先用功率矩算法优化配电网各环网内开关状态，求得配电网优化重构的初步结果，然后采用邻域搜索算法进一步寻优。这样既保留了功率矩算法搜索速度快的优点，又弥补了功率矩算法在某些情况下重构方案不够理想的缺点。

2.2 功率矩算法的步骤

给定配电网络的初始状态，首先闭合一个联络开关，通过拓扑分析获取该联络开关所在环路的所有节点和支路，然后通过功率矩算法确定当前环路的断开支路，更新配电网络的网络结构。由于每一个联络开关对应一个环路，对其余所有联络开关作类似处理，即可得到该配电网络的所有环路信息及各环路的断开支路。图1所示33节点配电系统共有5个环路。

为了保证配电网络保持辐射状运行且网络中无孤立节点产生，正常运行过程中需保持常闭状态的开关不参与重构，也不属于任何一个环路，如图1中的支路B1。对于2个环路的公共支路集（如图1中环路1和环路4的公共支路B3、B4和B5），当其中一个支路上的分段开关断开时，公共支路集中其他支路开关必须保持闭合，以避免形成孤立节点。

基于功率矩的配电网第一层优化重构算法的流程图如图2所示，其主要步骤如下。

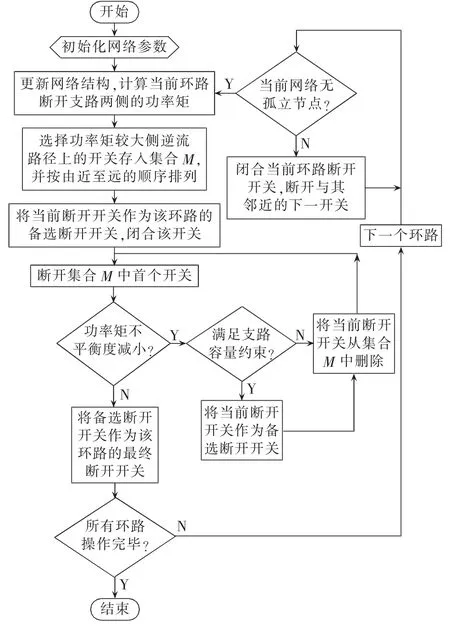
图2 功率矩重构算法流程图Fig.2 Flowchart of reconfiguration algorithm based on power moment

（1）计算当前环路的断开开关两侧节点的功率矩。选择功率矩较大一侧逆流路径上的分段开关作为候选断开开关的集合M，并将分段开关按照距离当前断开开关的距离由近到远顺序存储在集合M中。

（2）记环路中当前断开的开关为集合M中首个开关为闭合断开计算新断开支路两端节点的功率矩不平衡度。

（3）若开关所在支路的功率矩不平衡度大于开关对应的功率矩不平衡度，则将作为该环路的最优断开开关，转入步骤（4）；否则，判断新网络结构是否满足支路容量约束，若满足该约束条件，则将从集合M中删除，并将作为当前断开的开关，转入步骤（2），若不满足支路容量约束，则直接将从集合M中删除，转入步骤（2）。

（4）判断是否所有环路均已按上述步骤处理完毕，若是则第一层重构算法停止，将各环路中处于断开状态的支路所构成的开断支路集作为第一层优化重构的结果；否则转步骤（5），对下一个环路进行处理。

（5）对环路间的公共支路集，判断是否存在多个支路断开，以此为依据判断当前网络是否存在孤立节点，若无孤立节点，则转步骤（1），否则闭合当前环路中处于断开状态的开关，同时断开一个与其邻近的满足网络拓扑约束的开关，转步骤（1）。

3 基于邻域搜索的第二层优化重构

通过功率矩算法得到的重构结果大致确定了使网络损耗较小时各个环路内的断开开关所在的位置。为了进一步获得使目标函数更优的重构方案，需要在第一层优化重构方案的基础上，对各环路断开开关邻域内的开关借助潮流计算进行第二层优化搜索，通过对当前解的邻域范围进行搜索获得目标函数值更优的新解，并对新解继续进行邻域搜索，直至目标函数不再下降，从而得到最终的优化重构方案。

3.1 邻域的概念

某一断开开关的邻域是指在该开关所属环路内，分别沿顺时针方向和逆时针方向与已断开开关相邻的开关所构成的集合。如图1的环路1中，对支路B33的开关，其邻域是由位于支路B20（逆时针）和支路B7（顺时针）上的开关所构成的。

基于邻域搜索的配电网优化重构算法采用与功率矩算法相同的环路划分方法，配电网中应处于常闭状态的开关所在的支路不属于任何一个环路，环路间公共支路集中的开关至多能断开其中的一个。

3.2 搜索策略

对配电网络的某一环路进行邻域搜索时，保持其他环路的开关状态不变，首先闭合该环路中处于断开状态的开关，再以该开关为起点分别沿顺时针和逆时针2个方向断开下一邻近支路的开关，从而得到2个新的网络结构。对其余所有环路完成上述操作，得到一组新的网络结构集合。然后按配电网重构模型中的约束条件对新网络集合进行可行解筛选，从满足约束条件的新网络结构集合和原网络结构中选择网损最小的结构作为当前最优网络结构。若该最优网络结构同原网络结构相同，则搜索停止并输出最优解；否则对当前最优网络继续进行邻域搜索。

以图1所示的33节点系统为例，对各环路进行邻域搜索，结果如表1所示。

表1 邻域搜索示例Table1 Examples of neighborhood searching

若忽略所有支路的对地导纳，对注入功率为零的浮游节点，断开其两侧任意一个支路的开关，系统的网络损耗均相同。因此，为避免邻域搜索提前终止，在沿着某一方向进行邻域搜索的过程中遇到浮游节点时，需跳过浮游节点连接的另一侧支路。如图3所示的IEEE 69节点配电系统［17］中，节点19为浮游节点，若当前对环路1的支路B18上的开关进行邻域搜索，则沿逆时针方向搜索到的支路为B17，而沿顺时针方向搜索时需跳过支路B19，搜索到的支路为B69。

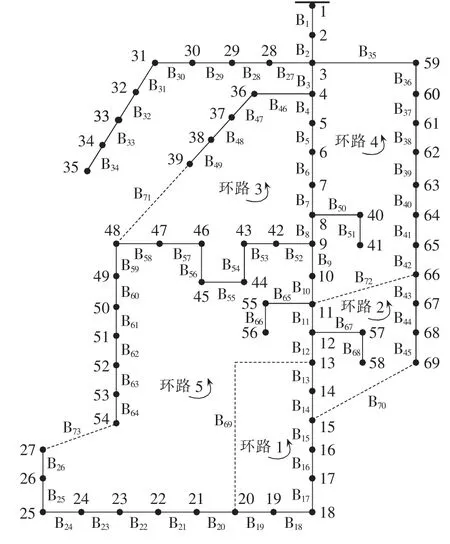
图3 IEEE 69节点配电系统Fig.3 IEEE 69-bus distribution system

3.3 基于邻域搜索的重构步骤

如图4所示，基于邻域搜索的第二层优化重构主要包括如下步骤。

（1）以前述功率矩算法得到的网络结构为重构的起点，按顺序选择一个环路。

（2）以当前环路中处于断开状态的支路（记为B0）为起点，沿顺时针方向进行邻域搜索。

（3）判断搜索过程是否遇到浮游节点，若是则进行跳过处理。

（4）断开邻域搜索得到的支路开关，闭合支路B0的开关，从而形成一个新的网络结构。

（5）判断新网络结构是否存在孤立节点，若无孤立节点，则将得到的该网络结构添加到集合T中。

（6）重新以B0为起点，沿逆时针方向进行邻域搜索，重复步骤（3）—（5）。

（7）判断所有回路是否处理完毕，若是，则本轮邻域搜索结束，转入步骤（8）；否则选择下一个回路，转入步骤（2）继续搜索。

（8）进行潮流计算，并选择集合T中网损最小且满足重构约束条件的网络结构作为当前最优解，并将其与本轮邻域搜索前的初始网络结构进行比较，若相同则算法停止，由各环路的断开支路所构成的开断支路集即为当前最优重构方案，否则，更新网络结构后转步骤（2），进行下一轮邻域搜索。

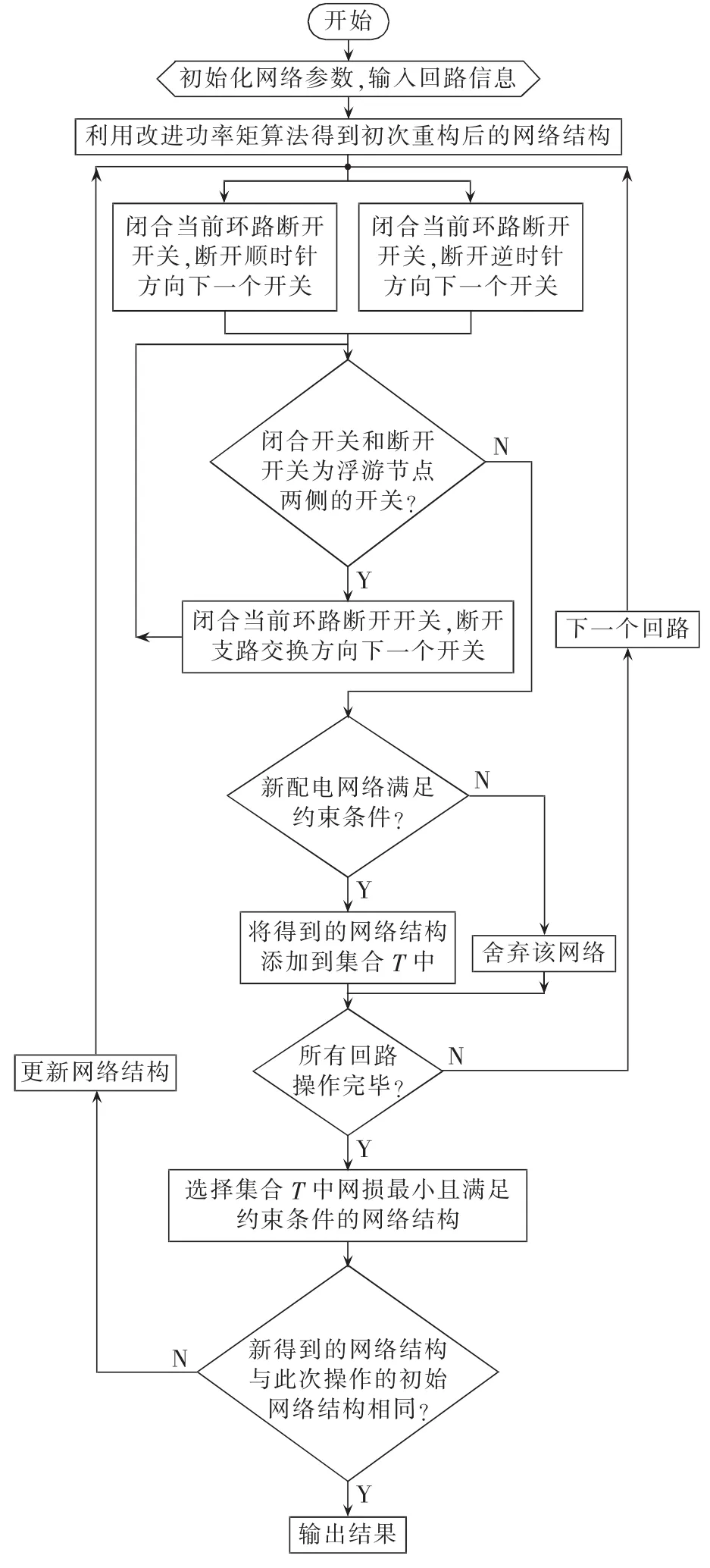
图4 邻域搜索重构算法流程图Fig.4 Flowchart of reconfiguration algorithm based on neighborhood searching

4 算例分析

4.1 算例1

采用图1所示的IEEE 33节点测试系统，该系统含37条支路，其中5条为联络支路，额定电压为12.66 kV，系统总有功负荷为3715 kW，总无功负荷为2300 kvar。DG采用恒功率模型，接入点及容量如表 2 所示［18］。

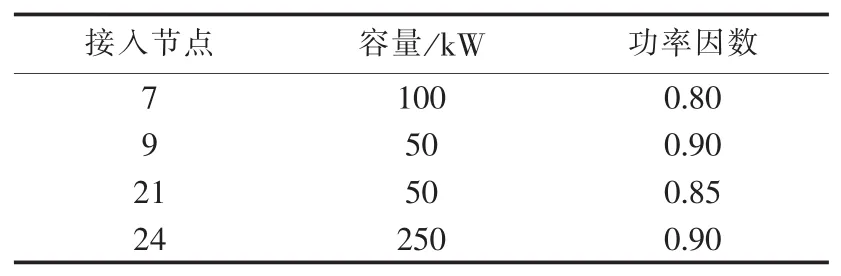
表2 DG接入位置及容量Table2 Location and capacity of installed DGs

首先采用功率矩算法对该系统进行第一层重构，结果如表3所示，表中每一个开断支路集对应一种可行的网络结构，随着对各环路的依次优化处理，系统网损逐步趋于降低。

表3 功率矩算法的重构结果Table3 Results of reconfiguration algorithm based on power moment

在此基础上，通过基于邻域搜索的第二层重构算法进一步对网络结构进行优化，结果如表4所示。可见对该配电网络，在功率矩算法结果的基础上仅需要2次邻域搜索即可使算法收敛，从而获得网损指标更优的网络结构。

表4 IEEE 33节点系统邻域搜索算法的重构结果Table4 Results of reconfiguration algorithm based on neighborhood searching for IEEE 33-bus system

图5则示出了两层优化重构之后含有DG的IEEE 33节点测试系统节点电压（标幺值）分布的变化情况，最低节点电压由重构前的0.919 p.u.提升至重构后的0.949 p.u.。

图5 IEEE 33节点系统重构前后的电压分布情况Fig.5 Voltage profile of IEEE 33-bus system before and after reconfiguration

表5示出了含DG和不含DG的IEEE 33节点测试系统重构结果（表中最低节点电压为标幺值）。可见通过重构降低了网络损耗，提高了最低节点电压，同时，DG接入配电网能在一定程度上降低网络损耗，对提高最低节点电压也具有一定的作用。

表5 IEEE 33节点系统重构结果Table5 Results of reconfiguration for IEEE 33-bus system

综合上述结果可见，对含有DG的IEEE 33节点配电网络，利用本文所提的两层优化重构算法可使网络损耗降低，系统运行电压水平得到明显改善。

4.2 算例2

为进一步验证本文算法对不同网络的适应性和有效性，以图3所示的IEEE 69节点网络为例进行测试，系统含74条支路，其中5条为联络支路，总有功负荷为3802 kW，总无功负荷为2694 kvar。

图6和图7分别示出了系统有功网损和节点电压（标幺值）在两层重构过程中的变化情况，经过第一层基于功率矩算法的网络重构，系统网损由最初的226.44 kW下降为156.85 kW，给出的重构方案是以｛B19，B70，B71，B10，B63｝为开断支路集的网络结构。第二层基于邻域搜索的网络重构则经过6次迭代，从新生成的48个网络结构中筛选出最优重构方案，对应的开断支路集为｛B69，B14，B58，B72，B61｝，系统网损由156.85 kW进一步下降为100.95 kW，最低节点电压则由重构前的0.908p.u.提升至重构后的0.942p.u.。

图6 重构过程中的网损变化情况Fig.6 Variation of net-loss during reconfiguration

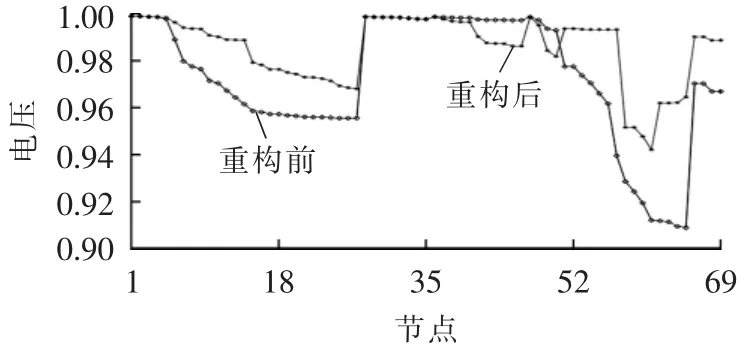
图7 IEEE 69节点系统重构前后的电压分布情况Fig.7 Voltage profile of IEEE 69-bus system before and after reconfiguration

4.3 算法性能

将本文算法的测试结果分别与文献［18］和文献［8］进行比较，相关数据列于表6，从中可以看出，对IEEE 33和IEEE 69节点测试系统，本文的优化方案与文献［18］和文献［8］相同，网损数值的差别是由于所用潮流算法和计算精度不同引起的。从算法的迭代次数和每次迭代过程中产生的网络结构数可知，本文方法不仅需要的迭代次数少，而且每次迭代过程中产生的新网络结构数目更少，从而需要进行的潮流计算次数也显著减少，而潮流计算正是配电网重构过程中耗时最大的环节，加之第一层基于功率矩算法的重构过程无需进行潮流计算，因此总体来看，本文所提方法所需计算量较小。另一方面，与采用随机搜索策略的群体进化算法［4，6-7，9］相比，本文方法在两层优化重构过程中均具有明确的搜索方向，因而搜索效率更高。

表6 重构算法比较Table6 Comparison between reconfiguration algorithms

5 结语

本文提出了一种基于功率矩算法和邻域搜索算法的配电网两层优化重构算法，首先利用功率矩算法进行第一层快速搜索，以获取配电网重构的较优解，在此基础上通过第二层邻域搜索算法，以较少的计算量获得目标函数更优的解点，克服了单纯的功率矩算法重构效果不理想且无法处理含有DG的配电网络的不足。通过对典型系统的仿真计算，验证了本文所提方法的有效性。

［1］MERLIN A，BACK H.Search for a minimal-loss operating spanning tree configuration in an urban power distribution system［C］∥5th Power System Computation Conference（PSCC）.Cambridge，UK：［s.n.］，1975：1-18.

［2］BARAN M E，WU F F.Network reconfiguration in distribution systems for loss reduction and load balancing［J］.IEEE Transactions on Power Delivery，1989，4（2）：1401-1407.

［3］张栋，张刘春，傅正财.配电网络重构的快速支路交换算法［J］.电网技术，2005，29（9）：82-88.ZHANG Dong，ZHANG Liuchun，FU Zhengcai.A quick branchexchange algorithm for reconfiguration of distribution networks［J］.Power System Technology，2005，29（9）：82-88.

［4］TAHBOUB A M，PANDI V R，ZEINELDIN H H.Distribution system reconfiguration for annual energy loss reduction considering variable distributed generation profiles［J］.IEEE Transactions on Power Delivery，2015，30（4）：1677-1685.

［5］ABDELAZIZ A Y，MOHAMED F M，MEKHAMER S F，et al.Distribution system reconfiguration using a modified Tabu search algorithm［J］.Electric Power Systems Research，2010，80（8）：943-953.

［6］欧帝宏，陈皓勇，荆朝霞.基于协同进化算法的配电网络重构方案［J］.电力自动化设备，2012，32（7）：108-113.OU Dihong，CHEN Haoyong，JING Zhaoxia.Distribution network reconfiguration based on co-evolution algorithm［J］.Electric Power Automation Equipment，2012，32（7）：108-113.

［7］刘继栋，王锡淮，肖健梅.基于十进制编码的差分进化算法在配电网重构中的应用［J］.电力自动化设备，2012，32（5）：94-97.LIU Jidong，WANG Xihuai，XIAO Jianmei.Distribution network reconfiguration based on differential evolution algorithm using decimal encoding［J］.Electric Power Automation Equipment，2012，32（5）：94-97.

［8］王淳，程浩忠.基于模拟植物生长算法的配电网重构［J］.中国电机工程学报，2007，27（19）：50-55.WANG Chun，CHENG Haozhong.Reconfiguration of distribution network based on the plant grow growth simulation algorithm［J］.Proceedings of the CSEE，2007，27（19）：50-55.

［9］WANG C，CHENG H Z.Optimization of network configuration in large distribution systems using plant growth simulation algorithm［J］.IEEE Transactions on Power Systems，2008，23（1）：119-126.

［10］崔金兰，刘天琪，李兴源.含有分布式发电的配电网重构研究［J］.电力系统保护与控制，2008，36（15）：37-40.CUI Jinlan，LIU Tianqi，LI Xingyuan.Network reconfiguration at the distribution system with distributed generation［J］.Power System Protection and Control，2008，36（15）：37-40.

［11］BEHDAD A，HOOSHMAND R A，GHOLIPOUR E.Decreasing activity cost of a distribution system company by reconfiguration and power generation control of DGs based on shuffled frog leaping algorithm［J］.Electric Power Systems Research，2014，61（10）：48-55.

［12］吴忠强，赵立儒，贾文静，等.计及DG与STATCOM的配电网重构优化策略［J］.电力自动化设备，2016，36（1）：111-116，122.WU Zhongqiang，ZHAO Liru，JIA Wenjing，et al.Optimal reconfiguration of distribution network with DG and STATCOM ［J］.Electric Power Automation Equipment，2016，36（1）：111-116，122.

［13］文升，顾洁，程浩忠，等.分布式电源的准入容量与优化布置的实用方法［J］.电力自动化设备，2012，32（10）：109-114.WEN Sheng，GU Jie，CHENG Haozhong，et al.Maximum penetration level and optimal placement of distributed genera-tion［J］.Electric Power Automation Equipment，2012，32（10）：109-114.

［14］王守相，黄丽娟，王成山，等.分布式发电系统的不平衡三相潮流计算［J］.电力自动化设备，2007，27（8）：11-15.WANG Shouxiang，HUANG Lijuan，WANG Chengshan，et al.Unbalanced three-phase flow calculation for distributed power generation system［J］.Electric Power Automation Equipment，2007，27（8）：11-15.

［15］董家读，黄庆，黄彦权，等.辐射型配电网重构的功率矩法［J］.电力系统保护与控制，2010，38（6）：22-25.DONG Jiadu，HUANG Qing，HUANG Yanquan，et al.The power moment method for radial distribution network reconfiguration［J］.Power System Protection and Control，2010，38（6）：22-25.

［16］GOSWNMI S K，BASU S K.A new algorithm for the reconfiguration of distribution feeders for loss minimization［J］.IEEE Transactions on Power Delivery，1992，7（3）：1484-1491.

［17］BARAN M E，WU F F.Optimal capacitor placement on the radial distribution systems［J］.IEEE Transactions on Power Delivery，1989，4（1）：725-734.

［18］曹文辉，彭春华，郭剑峰，等.基于全有效解整数微分进化算法的含分布式发电配网重构［J］.电力系统保护与控制，2013，41（11）：105-110.CAO Wenhui，PENG Chunhua，GUO Jianfeng，et al.Reconfiguration of distribution network with DGs based on the efficient solution and the integer coded differential evolution algorithm［J］.Power System Protection and Control，2013，41（11）：105-110.