基于SR-ITD的故障行波检测方法

李泽文，刘柏罕，熊 毅，赵 廷，郭田田，谭木子

（长沙理工大学 电网安全监控技术教育部工程研究中心，湖南 长沙 410076）

0 引言

随着电力系统规模的不断扩大、电压等级的提高和用户对电网安全的要求越来越高，精确故障定位成为快速排除故障、提高系统暂态稳定性的重要保证［1-2］。行波信号的检测准确度直接影响故障行波定位的准确性和行波保护的可靠性，行波信号的精确检测技术成为行波定位与保护技术发展的关键。

国内外专家对行波检测技术进行了深入研究，取得了大量的研究成果。文献［3-4］采用小波变换提取行波信号，该方法可以在一定程度的噪声中有效提取行波信号，但小波变换需要人为选取小波基的种类、分解层数，不具有自适应性，而不同的小波基和分解尺度会得到不同结果，在多点同步检测行波信号时易出现检测结果不一致的情况，影响故障定位精度与保护可靠性；文献［5-6］提出了采用希尔波特-黄变换HHT（Hilbert-Huang Transform）对故障行波信号进行检测，HHT具有自适应性，可用于检测故障行波信号，但存在模态混叠与端点效应的缺陷；文献［7］提出了基于固有时间尺度分解ITD（Intrinsic Time-scale Decomposition）的行波信号检测方法，该方法是一种自适应信号分解方法，可以避免行波波头信号分解存在的过包络、欠包络现象，并且受端点效应影响较小，具有较好的波头检测效果。目前利用软件检测行波信号的方法较多，在没有噪声或小噪声干扰下效果较好；但由于变电站内电磁干扰复杂，行波信号易被各种噪声信号淹没，增加了精确检测行波信号的难度。

为此，本文提出了一种基于随机共振-固有时间尺度分解SR-ITD（Stochastic Resonance-Intrinsic Time scale Decomposition）的分析方法。该方法对含大量噪声干扰分量的行波信号用随机共振方法进行处理，得到具有较大信噪比的行波信号，然后用固有时间尺度分解方法分析行波信号，实现行波信号故障特征信息的准确检测，较好地解决了强噪声干扰下变电站故障行波信号的精确检测问题。

1 随机共振基本原理

随机共振是一种噪声对弱信号起协助与增强输出作用的非线性现象。经典的随机共振原理可用一个过阻尼布朗粒子在双稳态势阱中的运动来解释［8］。可将双稳态系统的势函数描述为：

其中，a、b为系统结构参数，二者均大于0。

不妨将a、b的值均取为1，则可具体描述为1个极大值（在x=0处取得，即势垒）和2个极小值（在处取得，即势阱）构成势垒高为ΔV=a2/（4b）的系统，如图1 所示。

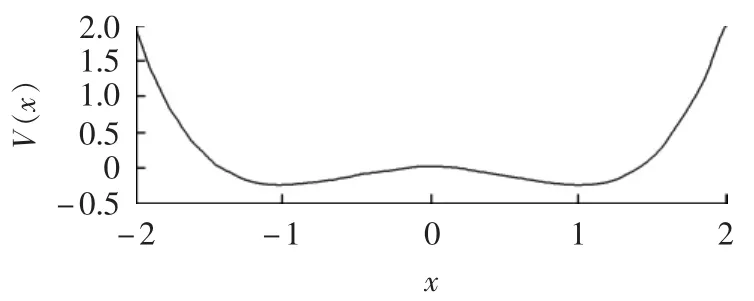
图1 双稳态系统势函数图Fig.1 Potential function chart of bistable system

随机共振系统中，朗之万方程是双稳态系统中典型的系统模型，可由如下方程描述：

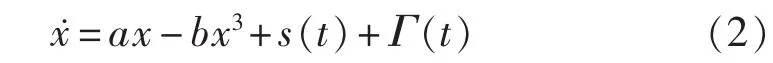
式（2）描述了粒子在同时受到输入信号s（t）和噪声Γ（t）驱动时，过阻尼布朗粒子在双势阱中进行阻尼运动。在周期力的作用下，令左右势垒的高度变化，使布朗粒子从一个势阱转移到另一个势阱中，这是由信号、噪声和非线性系统三者间的协同作用产生的，这种现象即为随机共振现象［8-10］。通过调节系统参数可改变势垒，使其与噪声强度大致相等，令系统产生最佳共振效果。

2 基于SR-ITD的行波信号分析方法

2.1 基于随机共振的行波信号分析

行波信号是一种瞬时突变信号，在随机共振中具有阱内共振的特点。单稳态随机共振模型中没有势垒，有且仅有1个稳态点，却依然能表现出良好的共振特性。单稳态随机共振是一种特殊的双稳态随机共振，为提取噪声干扰下的行波信号提供了一种有效的模型［11-12］。

由朗之万方程描述行波信号、噪声和非线性系统的共振模型：

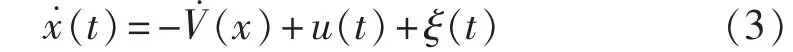
其中，（t）为行波信号共振模型输出信号的导数；u（t）为行波冲击信号；ξ（t）为均值为 0、方差为 D 的噪声信号；（x）为单稳态势函数模型的导数。

式（4）可表示为单稳态电力系统行波信号提取模型。

其中，a为行波信号模型参数，表示行波信号稳态点的位置，a≥0，即稳态点在x轴的右边；b亦为行波信号模型参数，b＞0。行波信号的提取需要优化参数a和b，通过调整参数a、b，分析对势函数变化的影响。考虑到行波信号的高频暂态特性，结合大量仿真中参数变化对结果的影响，得出适用于本文参数a、b的设定原则。

本文用变步长的随机共振方法提取行波信号，该方法通过改变行波信号采样步长h，令h＞1/fs（fs为信号采样频率），通过分析行波信号的高频暂态特性和采样频率，得出适用于行波信号的参数h的经验值范围为0.01～1［12-13］。改变行波信号单稳态模型中的参数a、b和h，能有效应用于强噪声干扰下行波信号的提取。

变步长单稳态随机共振模型提取行波信号流程图如图2所示。

通过构建行波信号单稳态随机共振模型，对行波信号中的参数a、b和h进行变步长随机共振处理。当随机共振设定参数、行波信号与噪声信号三者达到协同状态时，噪声向行波信号传递的能量最大，可把淹没在噪声信号中的有用信号有效分离出来，有效检测出噪声中微弱的行波信号。

强噪声干扰下的行波信号，经随机共振方法处理后，行波信号的信噪比得到了有效提高。但经随机共振方法处理后的行波信息辨识精度有限，由于 ITD方法具有较好的行波信号检测效果，因此本文选用ITD方法准确检测行波信号的特征信息。

图2 变步长单稳态随机共振法提取行波信号流程图Fig.2 Flowchart of traveling wave signal extraction by variable step-size monostable SR method

2.2 基于ITD的行波信号分析

ITD是近年来用于非平稳信号特征提取的方法，能有效分离行波信号。将行波信号分解成若干固有旋转分量和趋势分量，计算各个分量的瞬时频率。瞬时频率的突变体现为行波信号的突变，瞬时频率的突变时刻就是行波信号的到达时刻，因此利用ITD能够精确提取行波信号［14-15］。

假设Xt（t为时间）为行波信号，定义L为基线提取因子，将L作用于行波信号，剩下的信号定义为固有旋转分量，若用H表示固有旋转提取因子，则有H=1-L。由此将Xt进一步分解为：

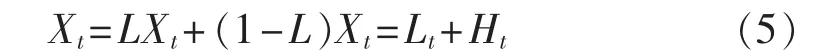
令｛Tk，k=1，2，…｝为 Xt的局部极值点，并定义T0=0。当Xt在某一时间间隔内为常数时，其极值Tk选择为该时间间隔的右端点。为了简化符号，用Xk和Lk分别表示 X（Tk）和 L（Tk）。

假设 Lt和 Ht的定义域为［0，Tk］，Xk的定义域为［0，Tk+2］。在连续极值点（Tk，Tk+1］范围内，可以定义一个基线提取因子L：

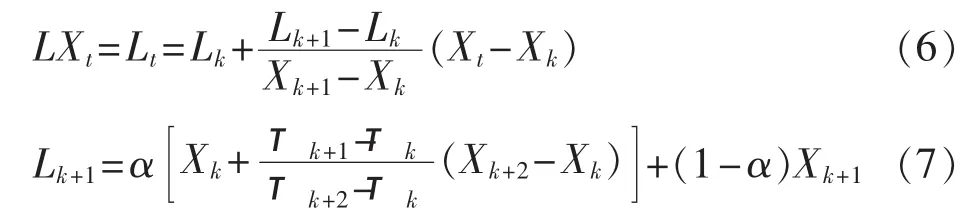
其中，0＜α＜1，α 一般取为 0.5。

按照式（6）和式（7）定义基线信号后，得到固有旋转提取因子H：

每分解一次，都将得到的基线信号重新作为输入信号继续分解，直到获得高精度的行波信号。

3 基于SR-ITD的行波信号仿真分析

输电线路发生故障且故障初相角较大时，行波信号幅值较大，不易被噪声信号干扰，现有的行波检测方法可有效提取行波信号。当故障初相角较小时，行波信号幅值较小，受变电站强噪声干扰，行波信号易被各种噪声淹没，现有的行波检测方法无法精确提取行波信号。

为此，本文以输电线路发生单相接地短路故障且故障初相角较小的情况为例进行仿真分析。仿真输电线路总长度设为100 km，设定在距离变电站A端45 km处发生单相接地故障，故障初相角为10°，变电站行波信号采集装置位于变电站的A、B两端，分别采集来自故障点的电流行波信号。行波采集装置的采样频率设为2 MHz，采样步长为5×10-7s，仿真总时间为1 ms。在仿真模型中叠加白噪声信号，使行波信号被完全淹没，利用线路给定参数可计算得波速为2.96×108m/s；再利用行波双端测量原理，对A、B两端采集的行波信号进行SR-ITD分析，准确检测出行波信号到达时刻，实现精确故障定位。

图3为A端叠加了信噪比为1dB白噪声信号后采集到的电流行波信号。由图可见，行波信号淹没于白噪声信号中，无法有效辨识行波信号。

图3 A端叠加白噪声后的电流行波信号Fig.3 Current traveling wave signal with superimposed white noise at Terminal-A

图4、图5分别为A端叠加白噪声后电流行波信号经小波变换和HHT后的波形图（图4中，幅值仅表示变换后幅值的数值，无单位；后同）。由仿真结果可知，直接对强噪声干扰下的行波信号进行小波变换和HHT，均不能有效检测行波信号。

图6为A端叠加白噪声的行波信号经随机共振方法处理后得到的波形图。由图可知，行波信号与白噪声信号经随机共振处理，调整a、b和步长h为a=b=1、h=0.12时，可较好地提高行波信号的信噪比，能较为准确地检测到行波信号。但行波信号附近仍有少量噪声干扰，需对行波信号进行去噪处理。

对A端叠加白噪声的行波信号经随机共振方法处理后，再用ITD进一步对信号进行去噪处理，使行波信号信噪比增大，突变点更为明显，A端经ITD去噪后的波形如图7所示。最后提取经ITD去噪后的行波信号的瞬时频率突变，即行波信号突变时刻。A端经SR-ITD处理后的波形如图8所示。

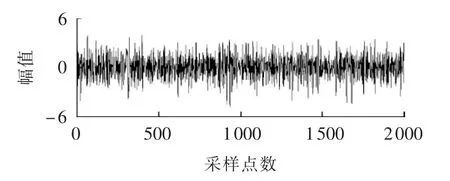
图4 A端叠加白噪声后，电流行波信号经小波变换波形图Fig.4 Current traveling wave signal with superimposed white noise at Terminal-A，after wavelet transform

图5 A端叠加白噪声后，电流行波信号的HHT波形图Fig.5 Current traveling wave signal with superimposed white noise at Terminal-A，after HHT

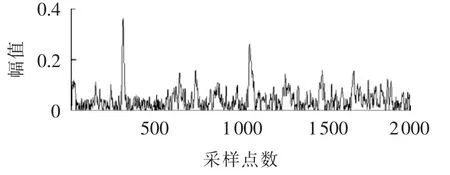
图6 叠加白噪声后，A端经SR法处理后的行波信号Fig.6 Current traveling wave signal with superimposed white noise at Terminal-A，after SR transform

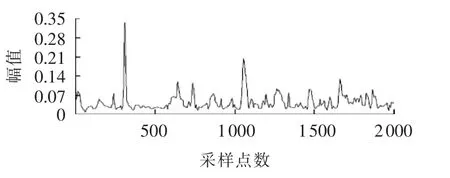
图7 A端经ITD去噪后的行波信号Fig.7 Current traveling wave signal with superimposed white noise at Terminal-A，after ITD transform

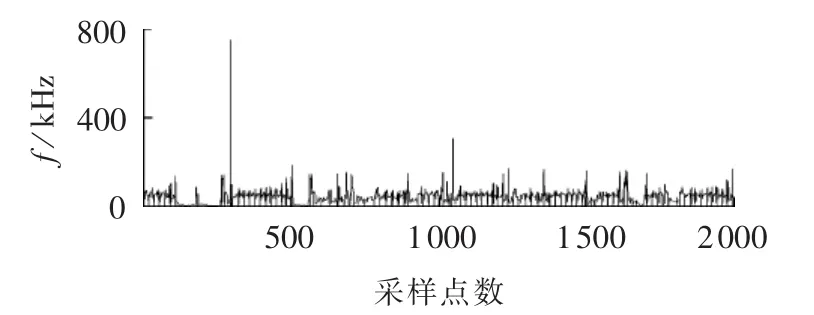
图8 A端经SR-ITD处理后的行波信号Fig.8 Current traveling wave signal with superimposed white noise at Terminal-A，after SR-ITD transform

同理可得行波采集装置提取的B端经随机共振和经SR-ITD处理后的电流行波分别如图9、10所示。

图9 B端经SR法处理后的行波信号Fig.9 Current traveling wave signal at Terminal-B，after SR transform

图10 B端SR-ITD处理后的行波信号Fig.10 Current traveling wave signal at Terminal-B，after SR-ITD transform

由图8、10可知，行波信号到达A端时行波采集装置记录点数为304，到达B端时行波采集装置记录点数为372。

由双端定位方法可求出故障点与A端的距离为：

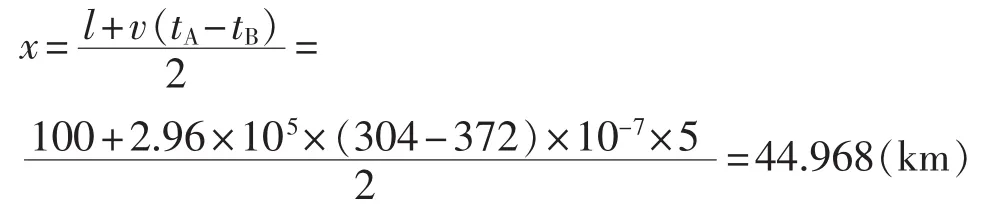
其中，l为配电线路长度；x为故障点与A端的距离；tA为行波到达线路A端的时间；tB为行波到达B端的时间；v为行波的传播速度。

故障点与A端的实际距离为45 km，易得出测量误差为32 m。

通过仿真分析和计算可知，本文提出的SR-ITD方法在强噪声干扰下能有效检测出故障行波信号，准确提取行波信号突变时刻，满足了电力系统故障定位的精度要求。

4 SR-ITD方法与其他方法的比较

为了检验本文方法的有效性，在同等噪声条件下将本文方法与现有行波检测中常用的小波变换、HHT进行对比仿真分析。

在行波信号中叠加不同强度的白噪声，然后分别采用小波变换、HHT对混合信号进行处理。

叠加白噪声的行波信号信噪比数值大小分别为10 dB、20 dB、30 dB、40 dB 时，采用小波变换处理信号，得出的仿真波形如图11所示。

由图11（b）、（c）、（d）可知，当行波信号叠加白噪声，使信号的信噪比大于等于20 dB时，小波变换能较好地消除噪声对原始信号的干扰，有效提取行波信号。由图11（a）可知，当行波信号叠加白噪声，使信号的信噪比小于10 dB时，噪声对小波变换干扰较大，此时小波去噪效果较差，小波变换无法准确提取行波信号的模极大值，行波信号将会与干扰噪声混淆，行波信号提取效果不佳，易增大故障定位误差，严重时甚至可能导致定位失败。

叠加白噪声干扰得到不同信噪比的行波信号，采用HHT处理信号后得出仿真波形如图12所示。

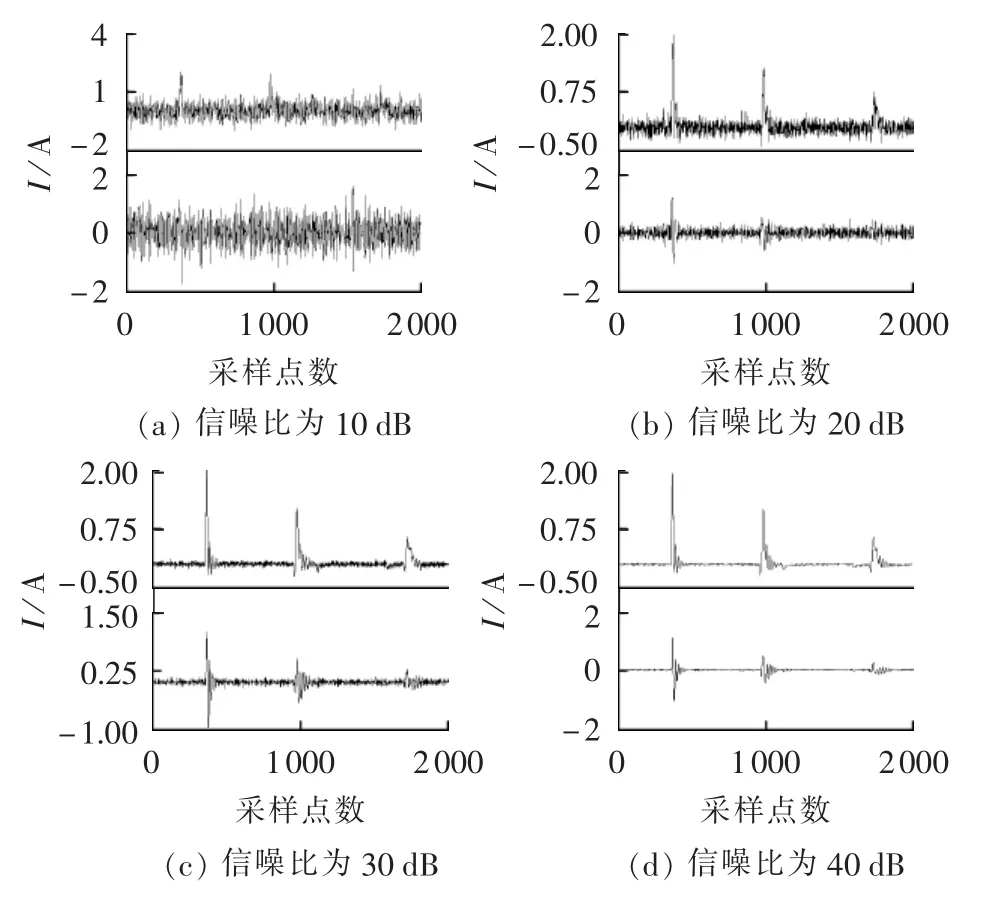
图11 不同信噪比下利用小波变换提取的行波信号Fig.11 Traveling wave signals extracted by wavelet transform for different SNRs

图12 不同信噪比下利用HHT提取的行波信号Fig.12 Traveling wave signals extracted by HHT for different SNRs

由图12可见，叠加白噪声后行波信号的信噪比大小分别为 10 dB、20 dB、30 dB、40 dB 时，HHT 受噪声的干扰影响较大，无法观测到明显的突变点，产生模态混叠，经变换后的时频图波形杂乱散布，无法准确测量行波波头瞬时频率突变值，对行波信号的提取效果不佳，导致定位失败。

由仿真结果可知，在信噪比大于10 dB时，小波变换能有效提取行波信号；HHT对噪声信号的要求更为敏感，叠加白噪声的行波信号信噪比为40 dB时，仍无法准确提取行波信号。实际变电站内噪声干扰较强，行波信号易被噪声信号所淹没，因此对于变电站强噪声干扰下行波信号的提取，均不能直接采用小波变换、HHT方法。

通过上述比较可知，采用SR-ITD方法在变电站强噪声干扰下检测行波信号时，可准确提取行波信号故障特征信息，能有效检测淹没在强噪声干扰下的行波信号。

5 结语

本文提出了一种基于SR-ITD的行波信号检测方法。该方法运用随机共振方法处理行波信号，有效提高了行波信号的信噪比，然后对行波信号利用ITD方法进行分析，可准确检测行波信号，提高了现有行波检测方法在变电站强噪声干扰下的检测精度。仿真结果验证了所提行波信号检测方法较现有的行波提取方法有明显优势，实现了行波信号的精确故障定位，具有一定的应用价值。

［1］董新洲，王珺，施慎行，等.配电线路单相接地行波保护的原理与算法［J］.中国电机工程学报，2013，33（10）：154-160.DONG Xinzhou，WANG Jun，SHI Shenxing，et al.Principle and algorithm of traveling waves based single-phase-to-ground protection for distribution lines［J］.Proceedings of the CSEE，2013，33（10）：154-160.

［2］范新桥，朱永利，卢伟甫，等.基于多点电流测量的输电线路行波故障定位新方法［J］.电力自动化设备，2012，32（11）：39-45.FAN Xinqiao，ZHU Yongli，LU Weifu，et al.Traveling wave fault location based on multiple current measurements for transmission line［J］.Electric Power Automation Equipment，2012，32（11）：39-45.

［3］姚李孝，赵化时，柯丽芳，等.基于小波相关性的配电网单相接地故障测距［J］.电力自动化设备，2010，30（1）：71-74.YAO Lixiao，ZHAO Huashi，KE Lifang，et al.Single-phase grounding fault locating based on wavelet correlation for distribution network［J］.Electric Power Automation Equipment，2010，30（1）：71-74.

［4］何正友，钱清泉.基于小波变换的信号奇异性指数计算方法及其应用［J］.电力自动化设备，2000，20（3）：12-15.HE Zhengyou，QIAN Qingquan.A computationalapproachto signal singularity exponent based on wavelet transform and its application［J］.Electric Power Automation Equipment，2000，20（3）：12-15.

［5］束洪春，赵文渊，彭仕欣.配电网缆-线混合线路故障选线的HHT检测方法［J］.电力自动化设备，2009，29（5）：4-9.SHU Hongchun，ZHAO Wenyuan，PENG Shixin.Faulty line selection based on HHT detection for hybrid distribution network［J］.Electric Power Automation Equipment，2009，29（5）：4-9.

［6］张小丽，曾祥君，马洪江，等.基于Hilbert-Huang变换的电网故障行波定位方法［J］.电力系统自动化，2008，32（8）：64-68.ZHANG Xiaoli，ZENG Xiangjun，MA Hongjiang，et al.Power grid faultslocation with traveling wave based on Hilbert-Huang transform［J］.Automation of Electric Power Systems，2008，32（8）：64-68.

［7］李泽文，周卿松.基于ITD的电网故障行波信息提取新方法［J］.电测与仪表，2015，52（5）：67-72.LI Zewen，ZHOU Qingsong.A new method for extracting the traveling wave information of power network based on ITD ［J］.Electrical Measurement ＆ Instrumentation，2015，52（5）：67-72.

［8］李楠，刘福.微弱信号检测的3种非线性方法［J］.电力自动化设备，2008，28（4）：82-86.LINan，LIU Fu.Three nonlinearmethods ofweak signal detection［J］.Electric Power Automation Equipment，2008，28（4）：82-86.

［9］ZHANG Ying，WANG Taiyong，LENG Yonggang，etal.Application of stochastic resonance signal recovery［J］.Chinese Journal of Mechanical Engineering，2009，22（4）：542-549.

［10］谭继勇，陈雪峰，何正嘉.冲击信号的随机共振自适应检测方法［J］.机械工程学报，2010，46（23）：61-67.TAN Jiyong，CHEN Xuefeng，HE Zhengjia.Impact signal detection method with adaptive stochastic resonance ［J］.Journal of Mechanical Engineering，2010，46（23）：61-67.

［11］李继猛，陈雪峰，何正嘉.采用粒子群算法的冲击信号自适应单稳态随机共振检测方法［J］.机械工程学报，2011，47（21）：58-63.LI Jimeng，CHEN Xuefeng，HE Zhengjia.Adaptive monostable stochastic resonance based on PSO with application in impact signal detection［J］.Journal of Mechanical Engineering，2011，47（21）：58-63.

［12］郑仕谱.基于随机共振的弱信号提取方法研究［D］.杭州：浙江大学，2014.ZHENG Shipu.Research on weak signal extraction method based on stochastic resonance［D］.Hangzhou：Zhejiang University，2014.

［13］冷永刚.大信号变尺度随机共振的机理分析及其工程应用研究［D］.天津：天津大学，2004.LENG Yonggang.Mechanism analysis and engineering application of large signal variable scale stochastic resonance［D］.Tianjin：Tianjin University，2004.

［14］仇新艳，李付亮.基于ITD和K均值聚类的电能质量扰动分析与识别［J］.电力系统及其自动化学报，2015，27（8）：54-59.QIU Xinyan，LI Fuliang.Analysis and identification for power quality disturbance signals based on ITD and K-mean clustering algorithm［J］.Proceedings of the CSU-EPSA，2015，27（8）：54-59.

［15］黄建才，朱永利.基于改进固有时间尺度分解法的绝缘子泄漏电流去噪研究［J］.电工技术学报，2013，28（1）：57-64.HUANG Jiancai，ZHU Yongli.Research on de-noising of insulator leakage current based on improved intrinsic time-scale

（continued on page 133）（continued from page 125）deposition［J］.Transactions of China Electrotechnical Society，2013，28（1）：57-64.