求解PageRank问题的GMRES-Inout方法

顾传青,邵晨晨

(上海大学理学院,上海 200444)

·快报·

求解PageRank问题的GMRES-Inout方法

顾传青,邵晨晨

(上海大学理学院,上海 200444)

PageRank算法已经成为网络搜索中的核心技术.首先基于内外迭代法,运用预处理的思想,提出GMRES-Inout方法,即重启的GMRES方法修正的内外迭代法;然后,详细介绍该方法的具体过程及收敛性分析;最后,通过数值实验说明该方法的有效性.

PageRank;GMRES方法;内外迭代法;收敛性

Google搜索引擎以其著名的PageRank算法成为近年来最成功的搜索引擎之一[1]. 1998年PageRank算法由斯坦福大学的Page等[2]提出,该算法通过分析网络的链接结构获得网页的重要程度排名.PageRank问题就是求解Google矩阵A的首特征值1所对应的特征向量,即线性系统

的解,其中α∈(0,1)为阻尼因子,e=(1,1,···,1)T∈Rn,v=e/n,矩阵P由网页的超链接结构[3]所定义,n为矩阵P的维数.

自PageRank问题提出以来,出现了很多求解该问题的方法,其中最原始的就是经典的Power算法[2].Power算法采用迭代的思想计算矩阵的特征向量,其优点是方法简单、单次迭代的运算量小,缺点是线性收敛速度慢,尤其当阻尼因子α接近1时.因此,幂法的加速方法应运而生,比如二次外推法[3]、内外迭代法[4]、修正的幂外推法[5]、多步幂法修正的内外迭代法[6]等.另外,PageRank问题可以转化为求解线性方程组的问题,因此一些Krylov子空间方法被用于求解PageRank问题,例如广义极小残量(generalized minimal residual,GMRES)方法[7]、预处理和外推加速的GMRES方法[8]等.为了加快PageRank问题的求解速度,本工作基于内外迭代法,运用预处理的思想,提出了GMRES-Inout方法,即重启的GMRES修正的内外迭代法.

1 内外迭代法和重启的GMRES方法

因为eTx=1,由式(1)可得特征值问题x=Ax可以转化为求线性方程组

的解.根据PageRank问题中阻尼因子α越小,收敛速度越快的性质,Gleich等[4]通过引入比α更小的参数β,0＜β＜α,将式(2)转化为等价方程组

求解系数矩阵为(I−βP)的线性系统仍然是困难的.接着,Gleich等[4]提出了采用Richardson迭代法计算x(k+1).将式(4)的右端项记为f,即

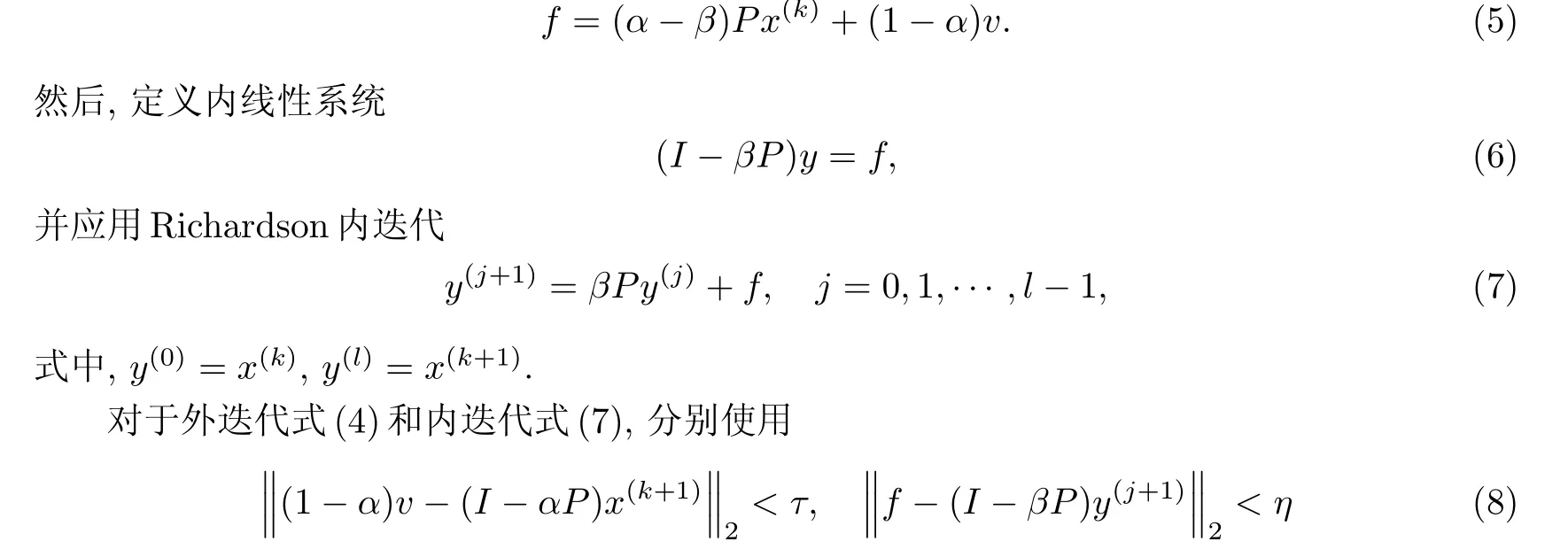
来判断迭代何时终止.式(8)中,参数η和τ分别是内、外迭代的收敛精度.

Saad等[7]提出的GMRES方法是一种求解稀疏线性系统的经典迭代方法.令b=(1−α)v,由式(2)可得

由于GMRES方法的时间复杂度和空间复杂度都较大,因此大多采用重启的GMRES方法[7-9].

算法1(重启的GMRES方法)

2 重启的GMRES方法修正的内外迭代法及收敛性分析

为了加快PageRank问题的求解速度,本工作提出一种新的算法:重启的GMRES方法修正的内外迭代(GMRES-Inout)方法.GMRES-Inout方法结合了内外迭代法和重启的GMRES方法的优点,基本思想如下:给定一个初始向量,利用重启的GMRES方法得到一个粗糙的解,若所求的解未达到收敛精度,则将解向量作为内外迭代法的初始向量,利用内外迭代法继续求解;否则重复上述过程,直至达到收敛精度.

算法2(GMRES-Inout方法)

步骤一给定重启步数m,初始向量x0,内、外迭代收敛精度η,τ,参数α1,α2,maxit用来控制内外迭代法的重启数,外迭代误差r=1,restart=0.

步骤二将算法1运行2～3次,若残差范数达到收敛精度τ,算法停止;否则继续.

步骤三将由重启的GMRES方法得到的近似解x1作为内外迭代法的初始向量,

3 数值实验

下面给出几种方法的数值实验结果.所有的数值实验都是在内存为4 GB、主频为1.8 GHz、处理器为AMD E2-3000M的计算机上使用Matlab(R2012b)进行的.

为了保证实验的公平性,所有方法均选取相同的初始向量x(0)=v(见式(1)).因为从理论和实践的角度,2-范数都是一种较好的选择,所以在本实验中将2-范数作为算法的终止准则.

为了测试算法的相对加速效果,定义加速比为

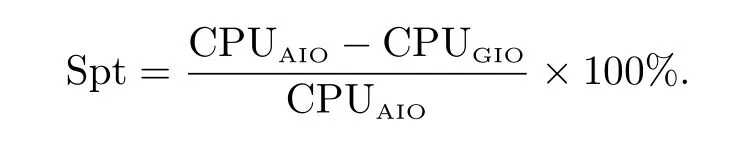
算例选取测试矩阵Web-Stanford,共包含281 903个网页和2 312 497个链接,其稠密度为0.291×10−2.表1给出了Inout方法、PIO方法、AIO方法、GIO方法的运算时间和矩阵向量积数.在GIO方法中,选取α1=α−0.1,α2=α−0.1,maxit=15.

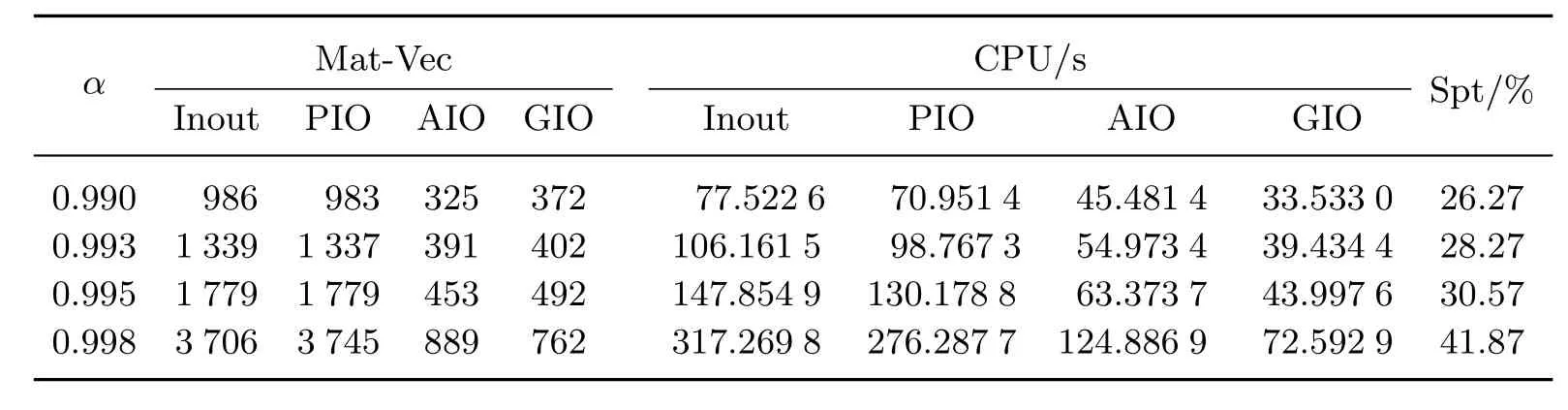
表1 对于测试矩阵Web-Stanford采用4种算法的比较结果Table 1 Comparison of various methods for the test matrix Web-Stanford

从表1中可以看出,GIO方法的运算时间最短,且相对于AIO方法有显著的改善.

[1]WU G,WEI Y M.A Power-Arnoldi algorithm for computing PageRank[J].Numerical Linear Algebra with Applications,2007,14(7):521-546.

[2]PAGE L,BRIN S,MOTWANI R,et al.The PageRank citation ranking:bring order to the web[R/OL].(2016-12-24)[2017-03-22].http://homepages.dcc.ufmg.br/vnivio/cursos/rill/sources/ pagerank.pdf.

[3]KAMVAR S D,HAVELIWALA T H,MANNING C D,et al.Extrapolation methods for accelerating PageRank computations[C]//12th International World Wide Web Conference.2003:261-270.

[4]GLEICH D F,GRAY A P,GREIF C,et al.An inner-outer iteration method for computing Page-Rank[J].SIAM Journal on Scientific Computing,2010,32(1):349-371.

[5]顾传青,王磊.一类修正的幂外推法加速PageRank计算[J].上海大学学报(自然科学版),2013, 19(2):150-153.

[6]顾传青,马先磊.求解PageRank问题的多步幂法修正的内外迭代法[J].应用数学与计算数学学报, 2014,28(4):454-460.

[7]SAAD Y,SCHULTZ M H.GMRES:a generalized minimal residual algorithm for solving nonsymmetric linear systems[J].SIAM Journal on Scientific and Statistical Computing,1986,7(3): 856-869.

[8]PU B Y,HUANG T Z,WEN C.A preconditioned and extrapolation-accelerated GMRES method for PageRank[J].Applied Mathematics Letters,2014,37(11):95-100.

[9]蒋尔雄.矩阵计算[M].北京:科学出版社,2008.

[10]HAVELIWALA T H,KAMVAR A D.The second eigenvalue of the google matrix[R/OL].(2016-11-21)[2016-012-20].http://ilpubs.stanford.edu:8090/582.

[11]GU C Q,XIE F,ZHANG K.A two-step splitting iteration for computing PageRank[J].Journal of Computational and Applied Mathematics,2015,278:19-28.

[12]GU C Q,WANG W W.An Arnoldi-Inout algorithm for computing PageRank problems[J]. Journal of Computational and Applied Mathematics,2017,309:219-229.

A GMRES-Inout algorithm for computing PageRank problems

GU Chuanqing,SHAO Chenchen
(College of Sciences,Shanghai University,Shanghai 200444,China)

The PageRank algorithm for determining the importance of Web pages has become a central technique in Web search.Based on the inout method,a GMRESInout algorithm which modifying the inner-outer method preconditioned with the restarted GMRES algorithm is proposed.Description and convergence analysis of the proposed algorithm are given.Numerical results are reported to demonstrate the efficiency of the proposed algorithm.

PageRank;GMRES algorithm;inner-outer iteration;convergence

TP 391.9;O 242.2

A

1007-2861(2017)02-0179-06

10.3969/j.issn.1007-2861.2016.07.010

2016-12-24

国家自然科学基金资助项目(11371243);上海市教委科研创新资助项目(13ZZ068);上海市重点学科建设资助项目(S30104)

顾传青(1955—),男,教授,博士生导师,博士,研究方向为数值逼近、数值代数及其应用.

E-mail:cqgu@staff.shu.edu.cn