求解混合整数规划问题的指数变差积分算法

于亚茹,姚奕荣

(上海大学理学院,上海 200444)

求解混合整数规划问题的指数变差积分算法

于亚茹,姚奕荣

(上海大学理学院,上海 200444)

研究了一种求解混合整数规划问题的指数变差积分算法.利用积分型总极小值理论及指数变差积分对混合整数规划问题进行研究,通过变差积分函数的分析性质及混合整数规划的最优性条件,结合牛顿法设计了一种求解混合整数规划的指数变差积分新算法.运用Monte-Carlo模拟方法实现整个算法,数值结果表明该算法是有效的.

混合整数规划;最优性条件;指数变差积分;Monte-Carlo模拟

混合整数规划问题已广泛应用于国际金融、通信、环境工程、工业和医疗等重要领域,特别是随着科学信息技术的飞速发展,研究人员对混合整数规划问题的发展越来越重视,同时也提出了很多不同于传统求解混合整数规划问题的方法[1-4].

Zheng[5-8]以丰满分析理论为基础提出了寻求优化问题全局最优解的积分水平集方法[9-12],该算法不需求解方向梯度,也不受初始点的影响,其优势恰能较好地处理不连续优化问题[6-7].之后Yao等[13]和Han等[14]又给出拟丰满函数和变差积分函数方法,并结合牛顿法实现了积分水平集算法的收敛性,其中变差积分函数针对总极值问题具有更好的性质,如凸性、单调性和可导性.此外,积分水平集方法在光学薄膜自动设计[15]、最优控制中的无变分迭代方法[16]、非线性对策[17]、偏微分方程的隐含解[18]、标准透镜的自动生成[19]和经济平衡点计算[20]等问题中都已得到了有效的应用.

2013年,Zheng等[21]提出了适合混合整数规划问题的积分水平集算法.该算法首先构造了一个Q-测度空间,使得混合整数规划问题在该空间中满足丰满分析理论;然后,证明混合整数规划问题满足(A),(M),(R)条件[6,22],并根据空间上的测度定义确定目标函数在水平集上的测度积分,证明最优性条件及算法的收敛性;最后,通过计算积分均值和方差来求解目标问题的全局最优解.

本工作在积分水平集算法基础上通过引入指数变差积分函数来讨论混合整数规划问题的求解问题.针对混合整数规划问题,运用不同的变差积分函数方法有更有效的结果.

考虑如下混合整数规划问题:

一定条件下序列{ck+1}收敛于最优值,{Hck+1}收敛于总极值点.在算法的实现上,选择用Monte-Carlo模拟方法进行数值逼近,这样使得算法和程序设计比较简单,然后通过数值算例说明本算法的可行性.

1 积分总极值理论

首先介绍有关混合整数规划问题的丰满分析理论,包括Q-测度空间的构造和丰满性证明.

设f为Rn上的下半连续且上丰满的函数.Ω1是Rn的集族,Ω2是Zm的幂集.由拓扑空间的定义可知,(Zm,Ω2)是离散拓扑空间.构造乘积拓扑空间及Borel域:

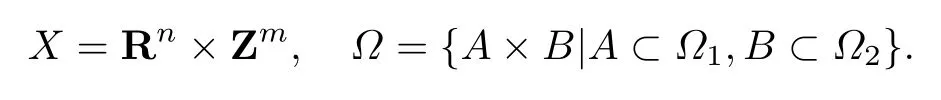
定理1[21](X,Ω,µ)是Q-测度空间.

证明由(Zm,Ω2)是离散的拓扑空间可知,Zm中的每个集合既是开集又是闭集,Ω2中的每个集合都是开的,并且每个非空开集的测度是正且有限的.因此(Zm,Ω2,µ2)是一个Q-测度空间.由于(Rn,Ω1,µ1)也是Q-测度空间,则对于Rn×Zm中任意的非空开集D=A×B,存在邻域O=O1×O2使得O⊂D,因此µ(D)≥µ(O)＞0.由上述分析得到(X,Ω,µ)也是Q-测度空间.

下面介绍乘积空间X=Rn×Zm中的性质.

性质1[21]设A⊂Rn,B⊂Zm,X=Rn×Zm是乘积拓扑空间,则有

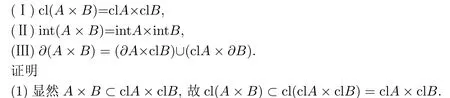
反之,设(x,y)∈clA×clB,并且W⊂X是含(x,y)的任意开集,于是存在含x的开集U(x)⊂Rn,含y的开集V(y)⊂Zm,使得(x,y)∈U(x)×V(y)⊂W.由于x∈clA,y∈clB, 故

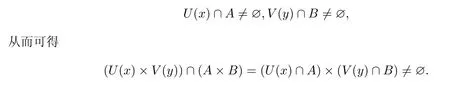
因此,(x,y)∈cl(A×B),即clA×clB⊂cl(A×B).故cl(A×B)=clA×clB. (2)显然intA×intB⊂A×B.由于intA×intB是X中的开集,故反之,设(x,y)∈int(A×B),于是存在含x的开集U(x)及含y的开集V(y)使得

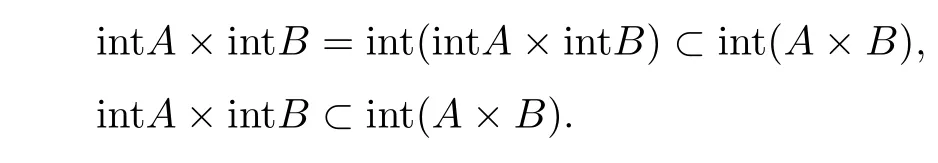
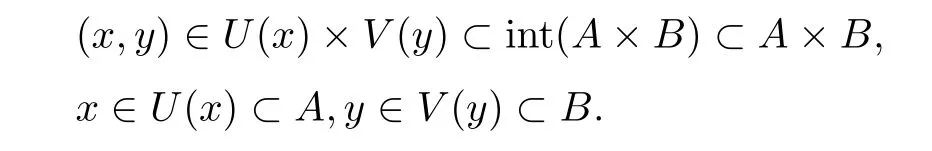
因此,x∈intA,y∈intB,即(x,y)∈intA×intB且int(A×B)⊂intA×intB. (3)由于∂(A×B)=cl(A×B)int(A×B),因此

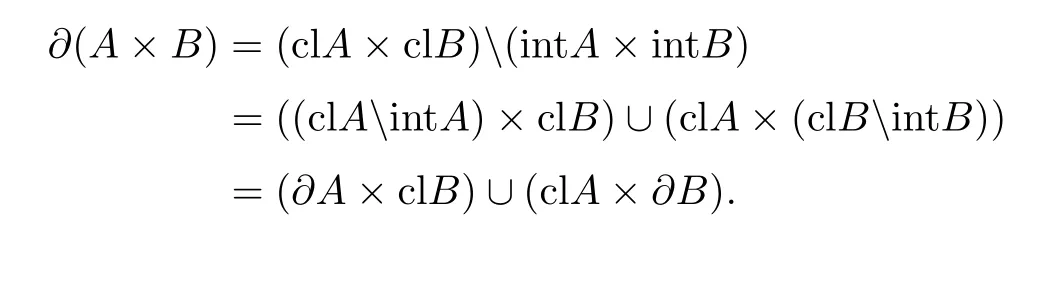
证毕.

由上述性质可以得到以下结论.

性质2[21]若对任意的A×B⊂X,A⊂Rn,B⊂Zm,A是Rn中的丰满集,则A×B 是X上的丰满集.

证明由(Zm,Ω2)是离散的拓扑空间可知B⊂Zm是开集且是上丰满的,故有也是丰满集.故f(x,y)在X上是上丰满的.

由上述定理和性质可知,f(x,y)在拓扑空间X上满足(A),(M),(R)条件:

(A)A×B是可测的丰满集且f(x,y)是下半连续函数;

(M)(X,Ω,µ)是Q-测度空间;

(R)f(x,y)是上丰满函数.

n-维Lebesgue测度空间(Rn,Ω,µ)是Q-测度空间.一个特定的总极值问题应考虑与之相适应的一个特定的Q-测度空间,一旦测度空间给定就可以用传统方式定义积分.

需要注意的是,特定的最优化问题需考虑与之相适应的特定的Q-测度空间.若一旦测度空间被确定,则测度易求.由于一个非空开集的内部是非空的,则包含非空丰满集的可测集的Q-测度总是正的,这是在最小化的积分途径中所必须的性质.因此通常作以下假设:

(A＇)D是可测的丰满集,f是D上的下半连续函数;

(M＇)(X,Ω,µ)是Q-测度空间;

(R＇)f是上丰满函数.

2 指数变差积分途径

2.1 指数变差积分函数及数学性质

(4)假设Δc＞0(Δc＜0的证明方法类似),当c＞c∗时,有

2.2 最优性条件

下面给出混合整数规划问题的最优性条件.设

矛盾.故定理得证.

2.3 指数变差积分算法

因此,由最优性条件可知c−=c∗是总极小值.

令x∈H∗,对k(k＞k0)有f(x,y)≤ck.设k→∞,可以得到f(x,y)≤c∗.但是对区间X上的所有(x,y),有f(x,y)≥c∗,因此H∗={(x,y):f(x,y)=c∗,(x,y)∈X},即H∗是总极小值点集.

3 数值算例

以下算例运用Monte-Carlo模拟方法结合指数变差积分算法进行计算,其中指数变差积分函数为

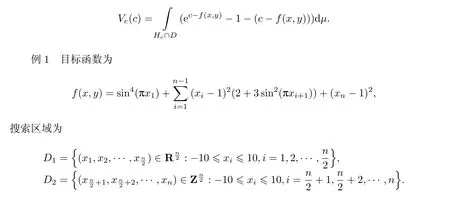
最优解为x∗=(1,1,···,1),f∗=0,λ＜1.0×e−10.运用指数变差积分算法进行计算,数值结果如表1所示.

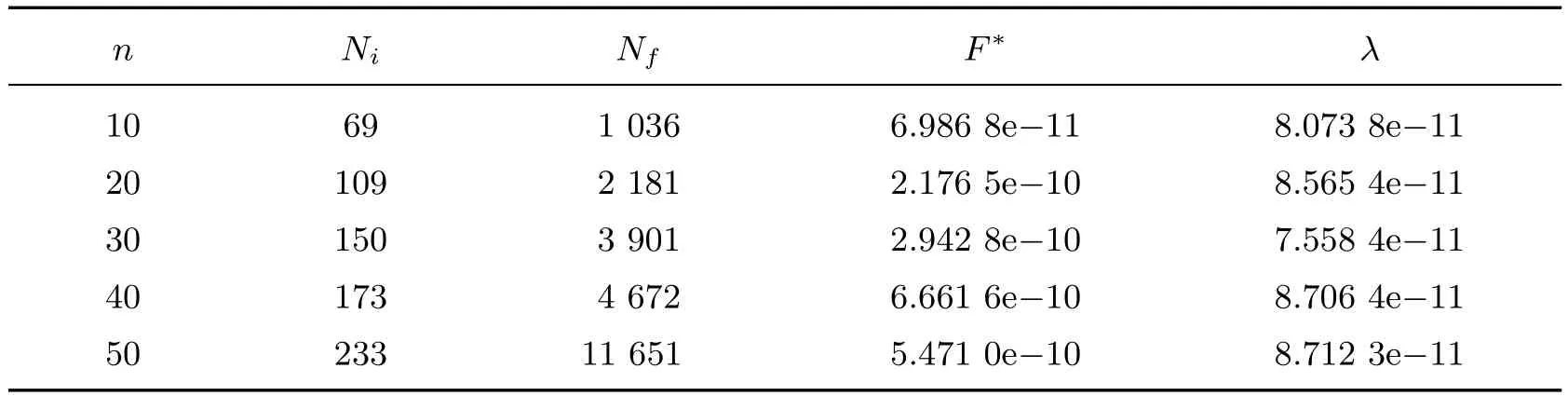
表1 例1的数值计算结果Table 1 Numerical results of Case 1

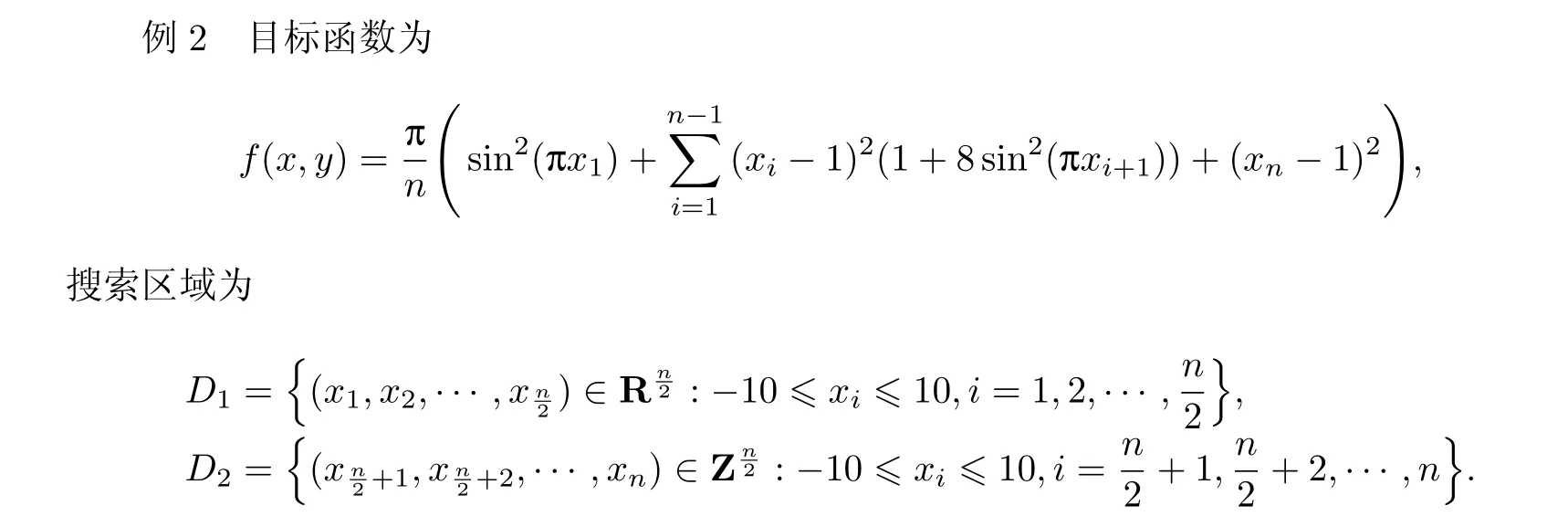
最优解为x∗=(1,1,···,1),f∗=0,λ＜1.0×e−10.运用指数变差积分算法进行计算,数值结果如表2所示.

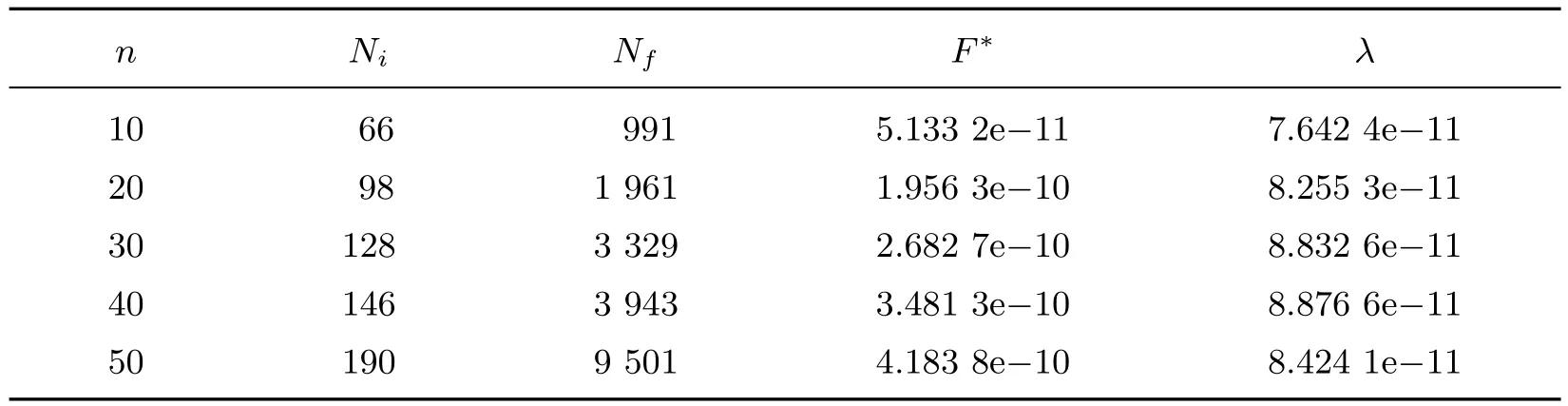
表2 例2的数值计算结果Table 2 Numerical results of Case 2

根据以上两个算例可以看出,当维数分别是10,20,30,40,50时,计算结果精度均满足条件λ＜1.0×e−10,这表明本算法是可行的.

4 结束语

本工作基于积分型总极小值理论,运用指数变差积分算法对混合整数规划问题进行了研究.不仅验证了变差积分函数的分析性质和混合整数规划的最优性条件,而且进一步结合牛顿法,设计了一种求解混合整数规划问题的指数变差积分算法.在算法实现过程中运用了Monte-Carlo模拟方法,但是偶尔会出现由于选取了特殊的初始值而导致算法结果异常,因此在计算水平集的具体实现上会有较大的研究空间.积分总极值方法具有坚实的分析理论基础,且具有较广的应用范围,对于一般的凸规划问题和不连续问题的求解都有较强的可行性.因此如何把积分总值方法应用于实际问题,例如投资组合、通信工程等现代领域,这将是值得深入研究的课题.

[1]BONAMI P,GONC¸ALVES J P M.Heuristics for convex mixed integer nonlinear programs[J]. Computational Optimization and Applications,2012,51(2):729-747.

[2]BERTHOLD T.Primal heuristics for mixed integer programs[D].Berlin:Technischen Universit¨at, 2006.

[3]ELHEDHLI S,GOFFIN J L.The integration of an interior-point cutting plane method within a branch-and-price algorithm[J].Mathematical Programming,2004,100(2):267-294.

[4]JOE N S.Interior point cutting plane methods in integer programming[J].Computers and Operations Research,2011,38(9):1335-1341.

[5]ZHENG Q.Robust analysis and global optimization[J].Annals of Operations Research,1990, 24(1):273-286.

[6]ZHENG Q.Robust analysis and global minimization of a class of discontinuous functions(Ⅰ)[J]. Acta Mathematical Applicatae Sinica(English Series),1990,6(3):205-223.

[7]ZHENG Q.Robust analysis and global minimization of a class of discontinuous functions(Ⅱ)[J]. Acta Mathematical Applicatae Sinica(English Series),1990,6(4):317-337.

[8]ZHENG Q.Robust analysis and global optimization[J].Computers and Mathematics with Applications,1991,21(6/7):17-24.

[9]BAZARAA M S,SHERALL H D,SHETTY C M.Nonlinear programming:theory and algorithms[M]. 3rd ed.New York:John Wiley&Sons,2006.

[10]ZHENG Q.Optimality conditions of global optimization(Ⅰ)[J].Acta Mathematicae Applicatae Sinica(English Series),1985,1(2):66-78.

[11]ZHENG Q.Optimality conditions of global optimization(Ⅱ)[J].Acta Mathematicae Applicatae Sinica(English Series),1985,1(3):118-132.

[12]郑权,蒋百川,庄松林.一个求总极值的方法[J].应用数学学报,1978,1(2):161-174.

[13]YAO Y R,CHEN L,ZHENG Q.Optimality condition and algorithm with deviation integral for global optimization[J].Journal of Mathematical Analysis and Applications,2009,357(2):371-384.

[14]HAN B S,YAO Y R.Existence and optimality of accessible and approximatable minimizers of quasi upper robust functions[J].Computers and Mathematics with Applications,2006,52: 65-80.

[15]TANG J F,ZHENG Q.Automatic design of optical thin-film system merit function and numerical optimization method[J].Journal of Optical Society of America,1982,72(11):1522-1528.

[16]GALPERIN E A,ZHENG Q.Variation-free iterative method for global optimal control[J].International Journal of Control,1989,50(5):1731-1743.

[17]GALPERIN E A,ZHENG Q.Integral global optimization method for nonlinear games[J]. Computers and Mathematics with Applications,1991,21(6/7):145-159.

[18]GALPERINA E A,PAN Z X,ZHENG Q.Application of global optimization to implicit solution of partial differential equations[J].Computers and Mathematics with Applications,1993, 25(10/11):119-124.

[19]ZHUANG S L,ZHENG Q,YU F T.Automatic generation of prototype lenses[J].Optics Letters, 1982,7(12):581-583.

[20]ZHENG Q,ZHUANG D.Equi-robust set-valued mappings and the approximation of fixed points[C]//Proceedings of the Second International Conference on Fixed Point Theory and Applications.1992:346-361.

[21]ZHENG Q,YAO Y R,ZHANG M L.An integral global optimization algorithm for mixed programming problem[C]//Proceedings of the 2013 International Conference on Advanced Mechatronic Systems.2013:25-27.

[22]SHI S Z,ZHENG Q,ZHUANG D M.Discontinuous robust mapping are approximately[J].Transactions of the American Mathematical Society,1995,347(12):4943-4957.

An exponent deviation integral algorithm for mixed integer programming

YU Yaru,YAO Yirong
(College of Sciences,Shanghai University,Shanghai 200444,China)

This paper studies an exponent deviation integral approach to the mixed integer programming problem.A deviation integral function with good properties is proposed,and the optimality condition for a mixed integer programming problem is examined.Then an exponent deviation integral algorithm is developed.Numerical calculation is performed using the Monte-Carlo technique to show effectiveness and feasibility of the algorithm.

mixed integer programming;optimality condition;exponent deviation integral;Monte-Carlo simulation

O 221.7

A

1007-2861(2017)02-0276-14

10.3969/j.issn.1007-2861.2015.05.010

2015-07-27

姚奕荣(1959—),男,副教授,博士,研究方向为运筹学与控制论.E-mail:yryao@staff.shu.edu.cn