基于菲涅耳变换的图像加密算法

郭绪坤,康显桂

(1.广州体育学院，广州 510500；2.中山大学 数据科学与计算机学院，广州 510006)

基于菲涅耳变换的图像加密算法

郭绪坤1,康显桂2

(1.广州体育学院，广州 510500；2.中山大学 数据科学与计算机学院，广州 510006)

针对相位截断加密算法无法抵御信息泄露问题，文章提出了一种基于相位截断菲涅耳变换与随机振幅掩模的加密算法，以抵御信息泄露问题；算法首先将原彩色图像分为3个独立的颜色通道，在对其进行菲涅耳变换后加入随机振幅掩模通道，将4个通道分别进行菲涅耳衍射截断处理；算法通过级联处理不仅提高了秘钥与密文间的关联性，还消除了信息泄露的风险；通过仿真试验与结果分析可知，本算法不仅在波长与自由空间传播错误距离参数、密文噪声、遮挡污染、密文泄露以及不同攻击等情况下有较好的鲁棒性，还解决了信息泄露问题。

相位截断；菲涅耳变换；图像加解密；彩色图像

0 引言

随着计算机和网络技术的快速发展，数字图像的处理日益便捷，这种便捷也给图像的信息安全造成了一定的负面影响，因此对图像进行加密处理是防止图像被截获篡改的有效方法。近年来，光学加密技术具有高速并行处理能力和灵活的加密自由度特性，相较于数字加密有着特殊的优势。光学加密相关算法成为当前研究的热点，其中大多数算法都是基于REFREGIER和JAVIDI提出的双随机相位编码加密技术[1-2]，比如分数傅里叶变换加密系统、扩展分数傅里叶变换加密系统以及菲涅耳变换加密系统等，这些加密系统的加密密钥和解密密钥是相同的，属于对称加密系统。而对称加密系统在遭受攻击时容易产生安全问题[3-5]。针对于此，大量文献对对称加密系统进行了改进，如文献[6]提出一种基于球面波照射的非对称光学图像加密算法，算法采用球面波的自带因子扰乱输入图像空间信息的方法实现图像的加解密；文献[7]提出一种基于衍射光学偏振选择与相位掩模的图像加密算法，克服了相位截断加密的鲁棒性缺失等；文献[8]提出了一种提出基于相位截断傅里叶变换的非对称加密系统，利用相位截断和两个公开的随机相位掩模产生具有实值并夹杂白噪声的密文，以克服对称加密系统中的安全问题。但大多数改进算法并没有解决加密系统中的信息泄露问题。菲涅耳变换是一种光学变换，最大的特点是有两个变换参数，与其他变换域相比具有更高的安全性，并且菲涅耳变换不需要光学透镜，两块相位板可以作为密钥，变换衍射的距离和波长也可以成为密钥，可控性强，操作简单。针对此，本文基于相位截断菲涅耳变换与随机振幅掩模，提出了一种新的非对称加解密系统。

1 菲涅耳衍射

衍射是指光波在传播的过程中，遇到狭缝、小孔或圆盘之类的障碍物后发生不同程度弯散传播的现象。而菲涅耳衍射指的是光波在近场区域的衍射。假设衍射挡板上有一点S′(x′,y′)发出的光波衍射到平面S(x,y)点(见图1)。衍射面到平面的距离为d，S′与S之间的距离为r。

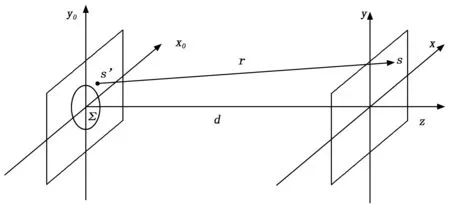
图1 基于相位截断菲涅耳变换的彩色图像加密过程

根据瑞利-索末菲衍射公式[9]得出S(x,y)处光波的复振幅为：

(1)

式中，cosθ=d/r表示倾斜因子，∑表示入射光波面上的一部分，θ为衍射角度，当θ较小忽略不计时，则可将k=2π/δ，则式(1)可改写为：

(2)

S′与S之间的距离为:

(3)

用二项式将距离r展开可得：

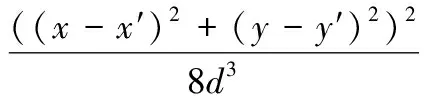
(4)

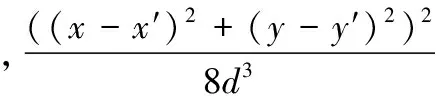
(5)

将式(5)代入式(2)中可得：

g(x,y)=FrT[f(x,y)]≈

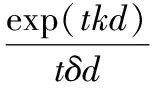
(6)

2 基于相位截断菲涅耳变换的加解密算法

2.1 彩色图像加密算法

彩色图像由红、绿、蓝3个颜色通道组成，设f(x,y)代表原彩色图像，其中红、绿、蓝3个颜色通道分别用fR(x,y)、fG(x,y)、fB(x,y)表示。一幅彩色图像中高频部分和低频部分分布是不均匀的，若是直接进行图像变换加密，当加密图像一旦被攻击解密后容易造成信息的泄露。为了扰乱原彩色图像的图谱信息，提高加密图像的信息安全，本文对原彩色图像进行菲涅耳变换后加入随机振幅掩模通道(RAM通道)。由此加密算法需要对4个通道进行菲涅耳变换(PTFrT)并加密。假设原彩色图像的红、绿、蓝与随机振幅掩模4个通道的波长分别用λ1、λ2、λ3、λ4表示，为简化分析，本文仅对单通道作详细分析，基于相位截断菲涅耳变换的彩色图像加密过程如图2所示。

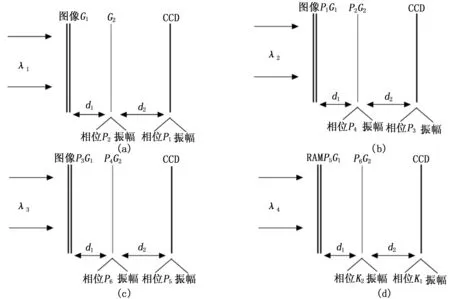
图2 基于相位截断菲涅耳变换的彩色图像加密过程

以图2为例，平行的一组光波照射图像，设光波长为λ1。函数G1(x,y)位于输入平面，函数G2(u,v)位于菲涅耳平面，两个函数为统计独立的随机相位掩模。设菲涅耳衍射的自由空间传播距离为d1，对菲涅耳衍射进行相位截断，则在G2之前获得的衍射振幅可表示为：

(7)

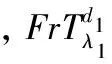
∬f(x,y)×

(8)

经过第二次距离为d2自由空间传播之后，CCD平面记录下加密密文CR(δ,σ)，可表示为：

(8)

设红色通道的解密秘钥为D2(u,v)和D1(δ,σ)，对其计算如下：

(9)

(10)

式中,PR{}为相位保持操作，可看出解密秘钥D2(u,v)、D1(δ,σ)与解密秘钥G1(x,y)与G2(u,v)有所差异。红色通道的解密图像可表示为：

(11)

(12)

绿、蓝、随机振幅掩模RAM通道的加密过程与红色通道类似，对G1(x,y)和G2(u,v)进行调制，可生成对应的加密秘钥。波长为λ2的绿色通道加密秘钥为：

EG1(x,y)=D1(δ,σ)·G1(x,y)EG2(x,y)=

D2(δ,σ)·G2(u,v) (13)

波长为λ3蓝色通道加密秘钥为：

EB1(x,y)=D3(δ,σ)·G1(x,y)EB2(x,y)=

D4(δ,σ)·G2(u,v)

(14)

波长为λ4的RAM通道加密秘钥为：

EM1(x,y)=D5(δ,σ)·G1(x,y)EM2(x,y)=

D6(δ,σ)·G2(u,v)

(15)

绿、蓝和随机振幅掩模RAM三个通道的加密过程见图2(b)～(d)。为了简化分析，设红、绿、蓝和随机振幅掩模通道4个通道的传播距离相等，在加密程序的最后，生成了两个解密秘钥K1(x,y)与K2(x,y) (见图2(d))。图3详细介绍了4个通道的加密流程。

图3 四通道加密流程图

如图3所示在加密过程中生成4个加密的密文分别为：CR(δ,σ)、CG(δ,σ)、CB(δ,σ)、CRAM(δ,σ)，其中红色密钥(D1,D2)、绿色密钥(D3,D4)和蓝色解密秘钥(D5,D6)不会公开。经过一系列的加密过程最终将各密文的解密秘钥K1(δ,σ)和K2(δ,σ)传输到最后，并将其记录下来。

2.2 彩色图像解密

彩色加密算法从红色通道开始加密，到随机振幅掩模RAM结束，而解密流程与之相反。图4为彩色图像解密算法的流程图。

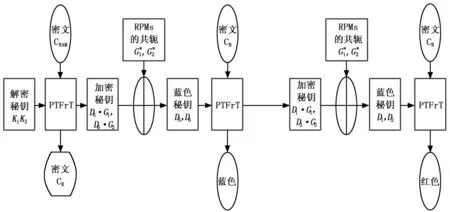
图4 彩色图像解密算法流程

首先使用解密秘钥K1(δ,σ)和K2(u,v)对随机振幅掩模RAM进行解密，解密过程中分别生成加密秘钥EM1(x,y)和EM2(u,v)：

(16)

(17)

(18)

(19)

(20)

利用解密秘钥D5(δ,σ)和D6(u,v)对蓝色通道进行解密得到解密秘钥依次对绿色、红色通道分别解密，解密流程如上图4所示。

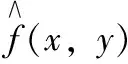
(21)

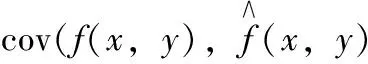
3 仿真试验与结果分析

本文PC机 (Intel(R)Corei3-3240CPU@3.4GHz4G内存) 在MATLAB7上仿真试验，对仿真实验中的参数设置如下：菲涅耳衍射的自由空间传播距离d1为65mm，第二次自由空间传播距离d2为95mm，原彩色图像的红、绿、蓝与随机振幅掩模4个通道的波长λ1、λ2、λ3、λ4分别为：633.2nm、536.9nm、442.6nm、598nm。

仿真实验选择lenna彩色图像(大小为512×512)，利用本文算法对其进行加解密处理，lenna彩色图像各通道加密密文如图5所示。

图5 lenna原图像各通道加密密文

上图5(b)～(e)分别为本算法对lenna图像处理所得的红色、绿色、蓝色和随机振幅掩模RAM通道的密文，密文中完全看不出图像信息。图5(f)为解密秘钥K1(δ,σ)的生成，图5(g)为解密秘钥K2(u,v)的结果，使用K1(δ,σ)和K2(u,v)两个正确秘钥后解密图像如图5(h)所示。此外，为了检验本算法的鲁棒性，使用RPM(G1(x,y),G2(u,v))与随机相位两个错误的解密秘钥来解密图像，图5(i)与(j)分别显示了解密图像结果，即使用错误秘钥无法获得原图像的任何信息。为了比较解密图像和原图像的相关性，本文将lenna原图像与解密得到的图(h)进行相关性计算，原图像与解密图像的相关系数值为1，由此可见，通过本算法可获得与原图像一致的解密图像。

3.1 本文算法对不同错误参数的鲁棒性

为了验证本算法对不同错误参数的鲁棒性，本算法利用不同波长与自由空间传播距离等参数对图像进行解密，结果如下图6所示。

图6 不同波长与自由空间传播距离误差解密结果

图6(

a

)为

RAM

通道10

nm

波长误差解密结果，其

RGB

三色通道的

MSE

值分别为(0.1552,0.0848,0.0588)从图中可图看出解密图像中无原图像任何信息；图6(

b

)为红色通道10

nm

波长误差的解密结果，其

RGB

三色通道的

MSE

值为(0.1292,1.9997×10

-25

,9.1979×10

-26

)，解密图像也没有原图像的颜色信息。图6(

a

)与(

b

)的红、绿、蓝三色相关系数值分别为(0.0006,0.0007,0.0062)与(0.2669,1.0,1.0)。出现上述结果是由于本算法为级联加密算法，

RAM

通道为第一解密通道，当

RAM

通道波长错误后三色通道的解密也受之影响。而红色通道是最后一个解密通道，错误的波长仅会影响自身。

图6(c)为RAM通道3毫米误差传播距离d1的解密图像，其RGB三色MSE值为(0.1356,0.0832,0.0314)，红、绿、蓝三色通道的相关系数值为(0.1202,0.0156,0.4282)。图6(d)为红色通道3毫米误差传播距离d1的解密图像，其红、绿、蓝三色通道的相关系数值为(0.3645,1.0,1.0)。图6(e) 为RAM通道3毫米误差传播距离d2的解密图像，其RGB三色MSE值为(0.1554,0.0716,0.0582)，对应的红绿蓝通道相关系数值为(0.0049,0.1526,0.0172)；图6 (f) 为红色通道3毫米误差传播距离d2的解密图像，其RGB三色MSE值为(0.0871,2.4756×10-26,5.5818×10-28)，对应的红绿蓝通道相关系数值为(0.3686,1.0,1.0)。可看出传播距离d1与d2的误差也会对解密图像造成明显的影响，传播距离误差对解密图像的影响与波长误差的影响接近。

3.2 本文算法对密文噪声和遮挡污染的鲁棒性

在图像的实际传输和存储等处理应用中，密文可能遭到破坏，健壮的加解密算法可以有效处理残缺的密文得到原加密图像。本文对密文噪声作鲁棒性测试，首先将零均值、不同标准偏差的高斯白噪声加入密文中。

图7(a)为相关系数为0.7162的解密图像效果，其高斯噪声的标准偏差为0.05，密文虽受到噪声污染但本文算法所得到的解密图像能显示出原图像的大部分信息。图7(c)为不同标准偏差下相关系数值的统计结果，由曲线可看出，解密图像的相关系数值随着噪声的下降而增加。

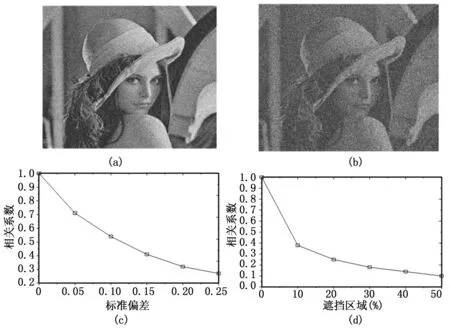
图7 本文算法对密文噪声和遮挡污染的鲁棒性结果

实验还测试了本算法对遮挡污染处理的鲁棒性。图7(b)显示的是相关系数值为0.3735、遮挡10%的解密图像。图7(d)为不同遮挡百分比下相关系数值的统计结果。通过曲线可以看出，解密图像的质量与遮挡范围成反相关。

3.3 本文算法对信息泄露的有效性

加密算法将原图像进行加密后，将信息隐藏到对应的密文和相位掩模秘钥中，一般情况下使用非密文或相位掩膜秘钥无法还原原图像，然而有些加密算法会发生信息泄露问题。下面验证本算法对信息泄露的有效性。

文献[10]算法分别对图像的红绿蓝三色通道进行独立加密，设3个通道的密文为T(δ,σ)，相位秘钥为PC(u,v)、PT(δ,σ)。图8(a)为文献[10]算法只对红色通道采用相位秘钥PC(u,v)进行解密的结果；图8(b)为文献[10]算法对三色通道仅使用相位秘钥PC(u,v)进行解密的结果；图8(c)为文献[10]算法对红色通道使用密文T(δ,σ)与相位秘钥PC(u,v)进行解密的结果；图8(d)为文献[10]算法对三色通道使用密文T(δ,σ)与相位秘钥PC(u,v)进行解密的结果；图8(e)为文献[10]算法对红色通道使用相位秘钥PC(u,v)与PT(δ,σ)，但不使用任何密文进行解密的结果；图8(f)为文献[10]算法对红绿蓝三色通道使用相位秘钥PC(u,v)与PT(δ,σ)，但不使用任何密文进行解密的结果。从图8(a)～(f)可看出，文献[10]算法即便使用不完整密文或相位掩膜秘钥也能获得原图像的部分信息，有信息泄露的风险，对信息泄露抵御性和有效性较低。而本算法红、绿、蓝三色通道的相位秘钥隐藏于级联系统之中，仅将K1(δ,σ)和K2(u,v)作为解密秘钥。图8(g)为本算法使用K2(u,v)进行解密的结果；图8(h)为本算法使用密文CRAM(δ,σ)与相位秘钥K2(u,v)进行解密的结果;图8(i)为本算法使用使用相位秘钥K1(δ,σ)与K2(u,v)进行解密的结果。由实验结果可知本算法在仅获悉部分秘钥与密文的情况下，无法获得原图像的任何信息。说明了本算法对信息泄露有很强的抵御性。

图8 两算法对对信息泄露的鲁棒性试验结果

3.4 本文算法对不同攻击的鲁棒性

仿真实验测试了本文算法在波长与自由空间传播距离不同错误参数、密文噪声和遮挡污染以及密文泄露不同情况下的鲁棒性。为了更充分的证明本文算法的健壮性，实验测试本算法对不同攻击的鲁棒性。

本文算法采用相位截断操作，使得输出与输入并无线性关系,因此本算法可抵御选择密文攻击、已知明文攻击、选择明文攻击等此类攻击。试验采用已知明文攻击与选择明文攻击对本算法进行测试，结果如图9所示。

图9 本文算法对不同攻击的鲁棒性结果

图9(a)为本算法对已知明文攻击的实验结果，图9(b)为本算法对选择明文攻击的实验结果，两种攻击的结果并没有获取到原图像的任何信息，算法抵御攻击的能力较强，说明本算法对部分常见攻击的鲁棒性较好。

4 总结

本文基于相位截断菲涅耳变换与随机振幅掩模，提出了一种新的非对称加解密算法，算法将原彩色图像分为三个独立的颜色通道，在对其进行菲涅耳变换后加入随机振幅掩模通道，将四个通道分别进行菲涅耳衍射截断处理，通过级联处理不仅提高了秘钥与密文间的关联性还消除了信息泄露的风险。用不完整解密秘钥无法获得原图像的任何信息，经过仿真验证本算法对波长与自由空间传播错误距离参数、密文噪声、遮挡污染、密文泄露以及不同攻击等情况下有较好的鲁棒性。

[1]PrfregiepP,JavidiB.OpticalimageencryptionbasedoninputplaneandFourierplanerandomencoding[J].OpticsLetters,1995,20(7):767-769.

[2] 周 琳,杜广朝,邵明省.基于双随机编码正交映射的全息图像加密[J].电视技术,2013,37(1): 24-27.

[3]DengX,ZhaoD.Single-channelcolorimageencryptionbasedonasymmetriccryptosystem[J].Opt.LaserTech,2012,(44):136-140.

[4]DengX,ZhaoD.Multiple-imageencryptionusingphaseretrievealgorithmandinter-modulationinFourierdomain[J].Opt.LaserTech,2012,44:374-377.

[5]HwangHE,ChangHT,LieWN.Fastdouble-phaseretrievalinFresneldomainusingmodifiedGerchberg-Saxtonalgorithmforlenslessopticalsecuritysystems[J].Opt.Express,2009,17:13700-13710.

[6] 丁湘陵. 基于球面波照射的非对称光学图像加密[J].激光技术, 2013, 37(5): 577-581.

[7]RajputSK,NishchalNK.Asymmetriccolorcryptosystemusingpolarizationselectivediffractiveopticalelementandstructuredphasemask[J].AppliedOptics, 2012, 51(22): 5377-5386.

[8]QinW,PengX.Asymmetriccryptosystembasedonphase-truncatedFouriertransforms[J].Opt.Lett,2010,35:118-120.

[9] 黎上芩.提高菲涅尔数字全息再现像质量的研究[D].大连:大连理工大学,2009.

[10]ChenH,DuX,LiuZ,etal.Colorimageencryptionbasedontheaffinetransformandgyratortransform[J].OpticsandLasersinEngineering, 2013, 51(6): 768-775.

Image Encryption Algorithm Based on Fresnel Transform

Guo Xukun1, Kang Xiangui2

(1.Guang Zhou Sport University, Guangzhou 510500,China; 2.School of Date and Computer Science Sun Yan-Sen University, Guangzhou 510006,China)

As the phase truncation encryption algorithm can not resist the problem of information leakage, this paper proposes an encryption algorithm of phase truncation Fresnel transform and random amplitude mask in order to resist information disclosure. Firstly, the original image is divided into three separate color channels in the Fresnel transform after adding random amplitude mask channel, and then the four channels were Fresnel diffraction truncation. The algorithm not only improves the relevance between the secret key and the ciphertext also eliminates the risk of information leakage through the cascade process. Through simulation experiment and result analysis, this algorithm not only has good robustness against the error distance parameter, the noise of the cipher, the pollution of the block, the leakage of the cipher and the different attack,but also solves the problem of information leakage.

phase truncate; Fresnel transform; Image encryption and decryption; color image

2016-10-12；

2017-01-05。

国家自然科学基金(61379155)；广东省教育厅2015重大科研立项青年项目(2015KQNCX078)。

郭绪坤(1981-)，男，硕士，讲师，主要从事多媒体信号处理、信息安全与图像加密方向的研究。

康显桂(1969-)，男，博士，教授，主要从事多媒体信息处理与图像处理方向的研究。

1671-4598(2017)05-0150-05DOI：10.16526/j.cnki.11-4762/tp

TP309.7;TN

A