基于模糊PID的磁悬浮球控制系统研究

王玲玲，吴华丽

(海军航空工程学院 控制工程系，山东 烟台 264000)

基于模糊PID的磁悬浮球控制系统研究

王玲玲，吴华丽

(海军航空工程学院 控制工程系，山东 烟台 264000)

针对磁悬浮球系统的本质不稳定性，设计模糊PID算法实现系统的稳定控制，并使之动态性能及稳态性能满足要求;文中首先分析了磁悬浮球系统的基本原理，并进行力学分析，建立系统的数学模型，并对其中的非线性部分进行了平衡点处的线性化，而后采用用PID控制设计，PID可以实现系统的稳定控制，且控制精度较高，但对于动态性能的改善不足，且当模型中的参数改变时，PID参数的适应性较差;因此在PID参数的基础上，采用模糊PID控制，使得系统既可以满足三性要求，又可以使其具有参数变化的适应能力。

磁悬浮球系统；PID；模糊PID；校正

0 引言

磁悬浮技术是指利用磁力克服重力使物体悬浮的一种技术，这种无接触的特性可以实现各种机械结构的高速、无摩擦运转，其工程应用一直是国内外研究的热点问题[1-3]。而磁悬浮系统是否能够实现高精度稳定控制，以及对系统当中参数摄动时的适应性，很大程度上取决于控制器的设计问题[4-5]，因此对于磁悬浮系统的研究具有非常重要的意义。本文以磁悬浮球系统为研究对象，设计控制器实现稳定控制，使得动态性能和稳态性能满足要求，并且使系统当参数改变时具有一定的适应能力。

1 磁悬浮球控制系统的基本原理

磁悬浮球系统通过带电的线圈绕组产生方向稳定、磁通大小随着励磁电流大小变化而变化的电磁场，且磁场方向垂直于电磁铁，此时位于磁场中的球体就会受到电磁力的吸引作用[6]。当产生的电磁力与球体的重力相等时，球体就可以悬浮于当中。球体的悬浮位置信息由光源和光电传感器组成的位置传感器反馈获得，如此便形成一个闭环反馈系统，如图1所示。本文就是针对此系统，研究控制器使之稳定并使得动态性能及稳态性能满足要求。

图1 磁悬浮球系统示意图

2 系统数学模型的建立

2.1 理论建模

考虑理想情况下，即忽略电磁铁的感抗对系统的影响，则磁悬浮系统的数学模型可以完全由竖直方向上的运动方程和电磁力方程给出，如下所示。

(1)

(2)

其中:F(i,x)为电磁力且为矢量；x为小球质心到电磁铁磁极表面的瞬时气隙；i为电磁铁绕组中的瞬时电流；m为小球的质量；常系数K为与空气磁导滤等定参数相关的量[1-3]。

对式(2)进行平衡点处的泰勒展开并线性化有:

(3)

对上式两端进行拉式变换可得传递函数模型为:

(4)

在实际系统中，是用电压来表示对气隙和电流的控制。其中电压与气隙的关系需要通过传感器标定来得出传感器的气隙-电压关系。而电压和电流的关系采用电压-电流型功率放大器，且在功率放大器的线性范围内，可以将这种电压电流关系表示为线性关系。如此得到下式：其关系式为:

(5)

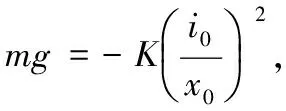
(6)

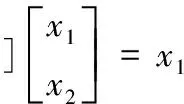
(7)

2.2 实际物理参数

表1给出具体参数取值，当实验系统不同时，参数要重新测量。另外，即便针对同一套系统，如果更改平衡位置时，带有*的参数要根据实际来测量和计算[6]。

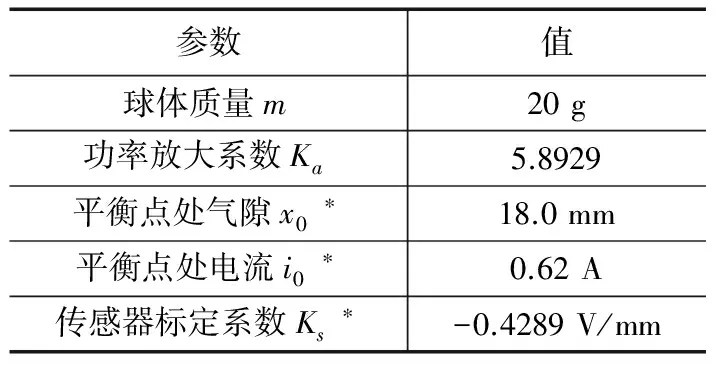
表1 系统的物理参数取值

将参数代入式(6)与(7)得到:

(8)

(9)

由式(8)可以看出系统有一个极点位于右半平面，因此磁悬浮球系统是本质不稳定的。由系统的可控可观性分析易知磁悬浮球系统既是可控的又是可观的，因此可以对系统进行控制器设计，使系统稳定。

3 PID控制设计

PID控制器是一种线性控制器，它根据给定值和实际值构成控制偏差，将偏差的比例、积分和微分通过线性组合构成控制量，对被控对象进行控制，如图2所示。

图2 PID控制系统原理图

利用MALTAB中的SIMULINK设计含有PID控制器的闭环控制系统，使系统稳定，并使性能指标满足调节时间ts≤0.2 s(2%)；超调量σ≤10%；稳态精度阶跃输入下ess≤0.05。

PID控制器中，Kp表示比例参数，Ki表示积分参数，Kd表示微分参数。根据PID参数调节的方式，当Kp=1.5，Ki=4.55，Kd=0.055，系统响应曲线如图3。此时系统的稳态精度达到指标，但是动态性能不足。继续调整参数至Kp=3，Ki=10，Kd=0.1，系统响应曲线如图4，此时超调量仍然较大。

图3 Kp=1.5、Ki=4.55、Kd=0.055时

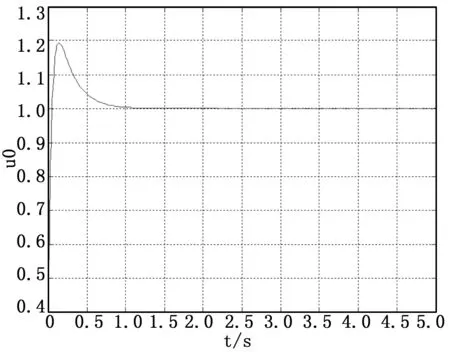
图4 Kp=3、Ki=10、Kd=0.1时

4 模糊PID控制设计

4.1 模糊PID控制器的结构

模糊PID控制器的结构主要由参数可调的PID和模糊控制器两部分组成，如图5所示。引入模糊PID的目的就是通过在每个采样时刻检测系统的偏差信号e和偏差信号变化率ec的大小，而后根据模糊规则得出PID参数的修正量，如此PID控制器就能根据系统响应的变化主动调节自身参数的大小，实现PID参数的自整定，从而增强系统的动态响应能力和对外界干扰的鲁棒性[7]。

图5 模糊PID控制器的结构图

4.2 模糊PID控制器的实现

仍然取式(8)为系统的模型，并根据图5模糊PID控制的结构图，系统的输入变量为气隙的偏差e和偏差变化率ec，输出量为PID参数的修正量ΔKp、ΔKi和ΔKd。其语言变量、基本论域、模糊子集、量化因子等信息如下表。

表2 模糊PID参数表

选择各变量的隶属度函数为均匀三角形[8-9]，并根据模糊PID参数在响应不同阶段的调整原则，并结合工程人员的技术知识和经验，设计出、和的模糊规则表[8-10]。而后根据表中的规则，在模糊控制器中添加模糊控制规则。

选取Centroid算法为解模糊方法，可以得到PID参数为修正量，而后根据如下公式得到控制参数。

Kp=ΔKp·qp+Kp0

Ki=ΔKi·qi+Ki0

Kd=ΔKd·qd+Kd0

(10)

其中:qp、qi和qd为比例积分微分的比例因子，Kp0、Ki0和Kd0为PID参数的初始值，可以通过常规PID得到。

4.3 试验结果与分析

当Kp0=3，Ki0=10，Kd0=0.1，图6为所有量化因子和比例因子为1时的响应，可以看到其响应的动态性能类似于常规PID。调整量化因子，当qe=2.5，qec=40得到图7，可以看出系统振幅减小，且各项性能指标满足要求。

图6 量化因子和比例因子均为1

图7 量化因子qe=2.5，qec=40

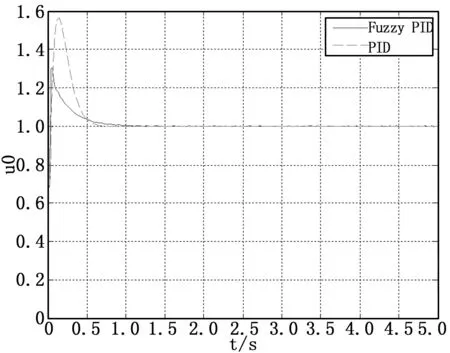
图8 标定系数Ks浮动

图9 标定系数Ks进一步浮动

5 结论

本文在忽略电磁铁感抗的影响下，使用磁悬浮球系统的二阶模型，分别设计PID控制器和模糊PID控制器使系统性能满足要求。仿真表明，PID控制对动态性能的改善较为困难，需要进行大量的参数调试，而模糊PID可以较为容易得使动态及稳态性能同时满足要求，且当系统参数浮动时，系统的适应性较好。但是，本文仅讨论了理想情况下，为了使系统仿真更具有参考价值，应考虑感抗影响，即使用三阶模型进行进一步研究。

[1] 李群明, 朱 伶, 徐 震. 磁悬浮球的鲁棒控制器设计[J]. 中南大学学报自然科学版, 2007, 38(5): 922-927.

[2] 王义进, 席文明. 磁悬浮球控制系统的设计研究[J]. 计算机测量与控制, 2007, 15(5): 608-609.

[3] 吕辉榜，刘小静，卢长明. 基于MATLAB的磁悬浮球实时控制设计及实验研究[J]. 仪表技术与传感器, 2009(5): 50-52.

[4] 薛炜杰. 基于MATLAB的磁悬浮控制系统研究[D]. 沈阳：东北大学，2008.

[5] 徐 林. 基于模糊PID的磁悬浮控制系统研究[D]. 哈尔滨：哈尔滨理工大学，2009.

[6] 磁悬浮实验装置[R]. 固高科技(深圳)有限公司，2006.

[7] 石辛民，郝整清. 模糊控制及其MATLAB仿真[M]. 北京：北京交通大学出版社，2008.

[8] 彭 辉, 徐锦华, 侯海良. 模糊控制在磁悬浮球系统实时控制中的应用[J]. 控制工程，2009, 16(3): 278-281.

[9] 邱 洪，黄苏丹，曹广忠. 基于DSP的磁悬浮球模糊PID数字控制器[J]. 武汉理工大学学报(信息与管理工程版), 2009, 31(6): 933-936.

[10] 徐锦华. 模糊控制方法在磁悬浮系统中的应用[D]. 长沙：中南大学，2009.

Research on Control System of Magnetic Levitation Ball Based on Fuzzy PID

Wang Lingling, Wu Huali

(Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)

In order to solve the nature unstable feature of the magnetic levitation ball system, fuzzy PID control algorithm was designed to realize the stability of the system, and also make the system satisfy the dynamic performance and steady-state performance. In this paper, firstly, the basic principle of magnetic levitation ball system was analysed, and mechanical analysis was made. Then the mathematical model was established, and the nonlinear part of the system is linearized at the equilibrium point. After that, PID algrithm was designed to realize stable control, with high accuracy and low dynamic performance, and while if the value of one parameter changed, system with PID control had low adaptability. Thus based on PID control, fuzzy PID algorithm was adopted, which make the system satisfy the performance of stability, accuracy and swiftness, and meanwhile make the system had the ability to adapt with parameters variation.

magnetic levitation ball system; PID; fuzzy PID; compensation

2016-12-10；

2017-01-09。

王玲玲(1984-)，女，安徽铜陵人，讲师，硕士，主要从事控制系统技术方向的研究。

1671-4598(2017)05-0109-03DOI：10.16526/j.cnki.11-4762/tp

TP

A