基于Zernike矩的保持架直径测量方法
2017-05-24孙建辉阮姣姣
孙建辉,阮姣姣
(浙江工业大学 机械工程学院,杭州 310000)
基于Zernike矩的保持架直径测量方法
孙建辉,阮姣姣
(浙江工业大学 机械工程学院,杭州 310000)
为了解决轴承保持架人工抽检费时费力等问题,同时提高工业生产自动化水平,简述了一种基于Zernike矩的保持架直径测量方法;以型号32007E的圆锥滚动轴承筐形保持架为例,提出了基于视觉的直径测量方法,分析CCD相机采集到的轴承保持架大小端面图像,进行图像预处理后,对Sobel算子边界点阈值进行重新设定,快速检测出保持架两端圆面可能存在的边缘点集,增加了有效圆检测算法,剔除部分偏离有效圆的点,再利用 Zernike 矩算子对有效的边缘点进行重新定位,检测出保持架两端圆面的亚像素边缘并计算其精确位置,最后对所得到的亚像素边缘点集进行最小二乘法拟合,获取保持架两端直径具体尺寸;实验表明,该方法测量结果与人工测量精度接近,甚至更高,具有良好的效果和实用价值。
直径测量;轴承保持架;Zernike矩;亚像素
0 引言
轴承保持架在实际加工过程中容易产生尺寸偏移等问题,若不及时发现,将影响轴承的正常工作。由于滚动轴承可分为滚针轴承、圆锥滚子轴承、圆柱滚子轴承、深沟球轴承等,根据滚动体的不同,轴承保持架侧边的形状也有所不同,但直径测量是他们的共同测量部分,因此,本文以圆锥滚子轴承筐形保持架为例,讨论直径测量问题。传统生产过程中一般通过人工测量的方法,测量速度慢,且容易产生视觉疲劳。目前机器视觉检测技术作为一种非接触式检测手段,由于其具有非接触、实时、在线、精度高等特点,已经在板材尺寸测量、车辆测距、工业CT图像检测等方面得到了广泛的运用[1-3]。
边缘检测是视觉测量的重要步骤之一,常用的边缘检测算子有Roberts、Prewitt、Canny等,这类算子只能做到像素级的边缘定位,且以微分运算为基础,对噪声敏感,检测结果很容易得到伪边缘,达不到精度要求。
亚像素边缘检测技术最早由Hueckel提出[4],主要的方法有拟合法、插值法和矩方法,其中矩方法应用最为广泛,Lyvers[5]等利用6个图像几何矩,计算出4个阶跃边缘参数,由于不具备正交性,因此图像处理时会出现兀余信息。Ghosal和Mheortal首次提出[6-7]了利用Zernike正交矩来检测亚像素边缘,建立理想的阶跃灰度模型,计算图像的三个不同阶次Zernike矩来确定4个参数,并以此为判断边缘的依据来确定图像的边缘。李金泉等[8]针对Ghosal算法中没有考虑模板效应,在边缘点的计算中加入了代表模板大小的参数N,改善边缘较粗的问题。但在实际应用过程中,Zernike多项式存在大量的阶乘和幂运算,计算较复杂,计算时间不能满足实际需求;曲迎东等[9-10]提出一种 Sobel-Zernike矩边缘算子,其检测精度与Zernike矩和Sobel算子接近,并在分析影响因素过程中,得出当图像中边缘点比率为87.75%时,Sobel-Zernike矩和Zernike矩运行时间相同,由于实际图像中边缘点占比率不可能超过50%,因此前者方法运算时间更短。本文在Sobel-Zernike矩算法基础上,对sobel算子边界点阈值进行重新设定,并增加有效圆检测,剔除残差较大的干扰点,提高定位精度,最后运用最小二乘法计算得到保持架两端圆直径尺寸。
1 Zernike 矩亚像素边缘检测算法
1.1 Zernike 矩定义
Zernike矩是一种正交矩,由Teague在1980年提出,一副连续图像f(x,y)的n阶m次Zernike矩定义如下[11]:
(1)
其中:*表示共轭,Vn,m为Zernike多项式,定义为:
(2)
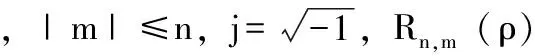
(3)
对于N×N的离散数字图像f(x,y)二维Zernike矩定义为:
Zn,m=∑x∑yf(x,y)Vn,m(ρ,θ)
(4)
1.2 基于Zernike矩的边缘检测原理
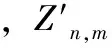
(5)
基于 Zernike 矩的边缘检测原理就是根据这一特性,建立理想阶跃灰度模型,通过像素点的3个不同阶次的Zernike矩,求解边缘检测所需要的参数h、Ø、l、k,最后将这4个参数作为边缘判据确定目标边缘。
图1为图像的亚像素边缘检测理想模型。其中, 圆为单位圆,直线L被单位圆包含的部分代表理想边缘,圆内L两侧的灰度值分别为h和h+k,k为灰度差,l为原点到边缘的理论距离,Ø为l和x轴的夹角。将图像顺时针旋转Ø角度后,得到图(b),此时直线L与y轴平行且关于x轴对称,旋转后的边缘函数f′(x,y)满足下式:
∬x2+y2≤1f′(x,y)ydxdy=0
(6)

图1 理想阶跃边缘模型
根据式(5)可得如下关系:
(7)
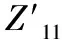
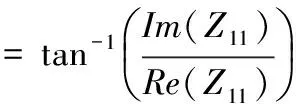
(8)
式中,Re(Z11)、Im(Z11)分别表示Z11的实部和虚部。
(9)
(10)
(11)
由式(7)、(10)、(11)进一步推导可得,
(12)
(13)
(14)
上面的公式推导中需要确定Z00、Z11、Z20这三个Zernike矩,本文选用曲迎东等[9]推导的7×7模板,利用模板对图像每个像素点的卷积运算得到对应的Zernike矩。考虑到模板的放大效应,最终边缘点的亚像素点坐标公式为:
(15)
其中:(xs,ys)表示边缘的亚像素坐标,(x,y)表示图1中原点的坐标。
2 基于Zernike的保持架直径测量
为方便测量两端面的直径及减少后续的计算量,处理过程中仅提取圆形ROI区域,且进行有效圆检测。具体算法步骤包括:(1)图像输入;(2)中值滤波,去除噪声;(3)阈值分割,将目标和背景分离;(4)Sobel边缘检测粗定位;(5)有效圆检测,剔除干扰点;(6)Zernike矩亚像素检测精定位;(7)最小二乘法拟合圆。
2.1 滤波与阈值分割
为增加检测精度,需对采集后图像去燥,由于中值滤波属于非线性滤波,对消除孤立的噪声点十分有效,且克服图像细节模糊等缺点,因此本文采用3×3的中值滤波对保持架图像进行处理。
图像分割主要目的是将背景和目标分离开以便于后续处理,图像分割最常用的方法是基于灰度阈值的分割。阈值分割步骤可以分为确定阈值和根据阈值划分图像。根据一定方法确定阈值t后,若像素点灰度大于阈值则判定为目标,否则为背景。本文采用最大类间方法(OTSU),遍历每个像素点的灰度t,分别计算目标和背景的像素点占整幅图像的比例ω0、ω1,平均灰度μ0、μ0,整幅图像的平均灰度μ,根据公式σ2=ω0(μ-μ0)2+ω1(μ-μ1)2,使得σ2最大时的t为最佳阈值。
2.2 Sobel算子边缘粗定位
保持架图像边缘的粗定位是利用基于一阶导数的边缘检测算子——Sobel算子,采用水平X方向、垂直Y方向小区域模板和图像卷积来近似计算梯度值G(x,y)。计算出每个像素点的梯度值后,根据设定的阈值T,若G(x,y)>T,则判定为边缘点。
(16)
其中:Gx(x,y)表示该点X方向的梯度分量,Gy(x,y)表示该点Y方向的梯度分量。
在边缘检测算法中,关键在于阈值T的选取。如果阈值取值过大,则出现的伪边缘就越多;如果阈值取值过小,则有效边缘点也可能被去除。因此,阈值的取值一般需要满足不丢失重要边缘、抗噪性好、计算简单等要求。阈值的选取方法很多,有全局阈值、局部梯度阈值[12]等,本文采用分割后图像的标准差作为阈值T进行边缘判断,即:
(17)
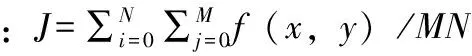
2.3 有效圆检测
为增加检测精度,本文在Sobel粗定位后增加了有效圆检测。有效圆检测是一种迭代法,在每一次迭代的过程中剔除残差过大的干扰点,直至满足条件。
G={(x1,y1),(x2,y2),…(xN,yN)},为Sobel粗定位后边缘点集,N表示当前像素点。具体步骤如下:
1)对点集G进行二乘法拟合,得圆方程(x-an)2+(y-bn)2=rn2,圆心坐标Gn=(an,bn),半径rn,n为迭代次数;
3)将残差{εn,i,i=1,2,3,…,Nn}从小到大排序,剔除排在末尾的Nn×c个点,c表示百分比,本文取c=70%,一次迭代后,边缘点集缩小为Gn+1。
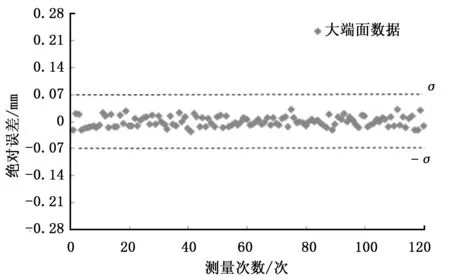
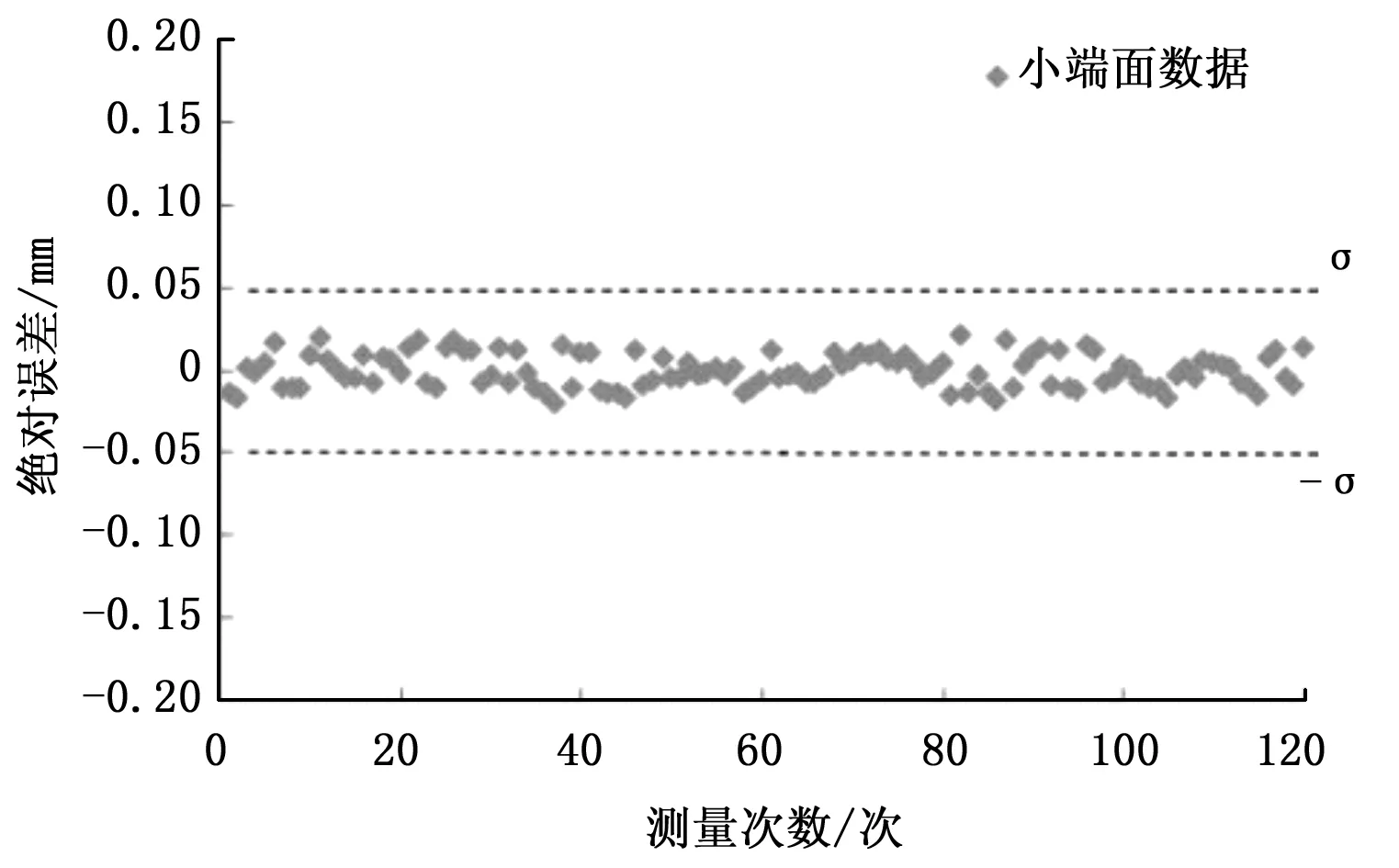
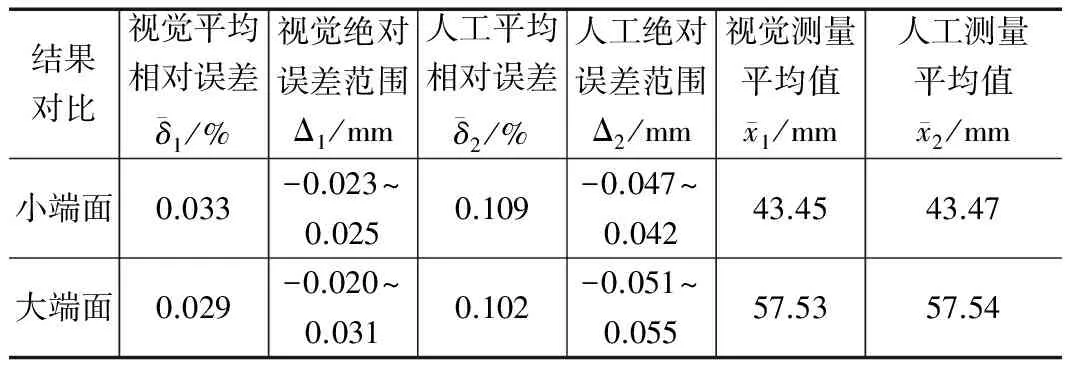
4)对点集Gn+1重新拟合,求得圆心坐标Cn+1=(an+1,bn+1),半径rn+1,当迭代前后圆心距dn 3.1 实验测量装置及编程环境 实验测量的光源为红外平面光源,由LED阵列来产生红外光,照明方式采用背光照明;选用黑白相机,型号为Basler aca2500-14gm,靶面尺寸1/2.5″,像素尺寸2.2 μm×2.2 μm;镜头为固定焦距25。实验编程环境为MatlabR2012a,采集到的图像大小648p×486p。由于固定焦距镜头的放大倍数与物面位置有关,为保证被测精度需使得被测特征处在同一物面上。因此本文实验分两次拍摄,分别对大端面外圆、小端面内圆进行尺寸检测。 3.2 测量对象 图2 保持架局部结构示意图 3.3 实验结果 第二组实验对小端面直径测量,测量结果如图4所示。图(a)为黑白相机拍摄图,和第一组实验方法相同,经过中值滤波和自适应阈值分割后得到图(b),其中最佳阈值t2=0.108,由图(b)可知保持架侧边坡面上均匀分布着的兜孔已分割为背景,这有利于减少后续算法的计算复杂度;图(c)为Sobel边缘检测结果,边界判定阈值T2=0.236 9,和第一组实验结果一样, Sobel检测后图像的边缘也是单像素tu宽度,内圆边界完整光滑,未见明显的锯齿状;图(d)为最终检测结果,有效圆检测迭代2次后,以相同方法得到内圆直径为130.6915(pixel)。 图3 大端面直径测量结果 图4 小端面直径测量结果 实验最后对一标准件在相同条件下进行实验测量,通过换算可得到最终保持架直径测量结果。 3.4 对比分析 图5和图6为对保持架应用本文算法检测后,计算得到绝对误差值。表1显示了为对检测结果进一步的分析计算,其中相对误差值由以下公式得到: (18) 其中,平均相对误差由各相对误差取平均值得到,视觉测量的两端面平均相对误差为0.033和0.029,人工测量的两端面平均相对误差为0.109和0.102,且视觉测量中小端面和大端面的绝对误差范围分别为[-0.023,0.025]和[-0.020,0.031],而人工测量小端面和大端面的绝对误差范围为[-0.047,0.042]和[-0.051,0.055],再比较两种测量方法的保持架直径平均值,视觉测量中小端面和大端面的直径平均值为43.45和57.53,人工测量中小端面和大端面的直径平均值为43.47和57.54。上述的比较可得,在相对误差和绝对误差上,视觉测量比人工测量所得到的结果更小,这表明视觉测量结果更接近观测值;另外,图5、图6的结果显示,对保持架的视觉检测,绝对误差值变化较平稳,不存在跃变现象,视觉检测结果满足手动测量得到的(-σ,+σ)误差范围,说明视觉测量结果有效,满足检测精度要求。 图5 大端绝对误差计算结果 图6 小端绝对误差计算结果 结果对比视觉平均相对误差δ1/%视觉绝对误差范围Δ1/mm人工平均相对误差δ2/%人工绝对误差范围Δ2/mm视觉测量平均值x1/mm人工测量平均值x2/mm小端面0.033-0.023~0.0250.109-0.047~0.04243.4543.47大端面0.029-0.020~0.0310.102-0.051~0.05557.5357.54 实验表明,本文算法的稳定性较好,将视觉测量结果和人工测量结果作比较后,可知基于Zernike的亚像素边缘测量结果和人工测量结果接近,在误差方面,视觉测量比人工测量得到的误差更小,证明本文提出的算法可行,有现实意义。 本文将Zernike亚像素边缘检测方法应用到保持架直径测量中,在Sobel-Zernike矩算法基础上,对sobel算子边界点阈值进行重新设定,在获得初步定位的边缘点集后,增加有效圆检测,剔除部分偏离有效圆的点,再利用Zernike矩亚像素检测方法进行边缘点判定并计算精确坐标,最后将这些坐标点进行最小二乘法拟合,计算出直径尺寸。实验证明,本算法确切可行,视觉测量数据和人工数据对比后,能够达到人工检测的精度要求,且在一定程度上避免了人工误检的可能性,直径圆的拟合也为后续检测保持架侧边窗孔的均匀分布情况提供一定帮助。 [1] 李江昀,王宇浩,童朝南.一种Zernike矩的高精度板材尺寸测量方法[J].电子学报,2015,43(7):1432-1436. [2] 伍济钢,宾鸿赞.薄片零件机器视觉图像亚像素边缘检测[J].中国机械工程,2009,20(3):297-300. [3] 陶 李,王 珏,邹永宁,等. 改进的Zernike矩工业CT图像边缘检测[J].中国光学,2012,5(1):48-56. [4]ZhaoBY,QiYJ.Improvedalgorithmforsub-pixeledgedetectionbasedonZernikemoments[J].AdvancedMaterialsResearch,2011,341-342:763-767. [5]EPLyvers,ORMitchell,MLAkey,APReeves.Sub-pixelmeasurementsusingamoment-basededgeoperator[J].IEEETran-sactiononPatternAnalysisandMachineIntelligence,1989,11(12):1293-1309. [6]GhosalS,MehrotraR.Detectionofcompositeedges[J].IEEETransactionsonImageProcessing,1994,3 (1) : 14-25. [7] 高世一,赵明扬,张 雷,等.基于Zernike正交矩的图像亚像素边缘检测算法改进[J].自动化学报,2008,34( 9):1163-1168. [8] 李金泉,王建伟,陈善本,等.一种改进的Zernike正交矩亚像素边缘检测算法[J].光学技术,2003,29(4):500-503. [9] 曲迎东,崔成松,陈善本,等.利用Sobel-Zernike矩算子的快速亚像素边缘检测方法[J].光电工程,2003,30(5):59-61. [10] 曲迎东,崔成松,陈善本,等.Sobel-Zernike矩亚像素边缘算子的影响因素分析[J].光电工程,2005,32(7):71-73. [11]TeagueMR.Imageanalysisviathegeneraltheoryofmoments[J].Opt.Soc.Am,1980,69(8):920-930. [12] 沈德海,侯 建,鄂 旭.基于改进的Sobel算子边缘检测算法[J].计算机技术与发展,2013,(11):22-25. Measuring Method of Cage Diameter Based on Zernike Moment Sun Jianhui, Ruan Jiaojiao (Zhejiang University of Technology, Hangzhou 310000,China) In order to solve the time-consuming and laborious problem of manual inspection of bearing cages, and to improve the level of industrial production automation, a method of measuring the diameter of cages based on Zernike moments is presented. Taking the 32007E cylindrical roller cage as an example, a vision-based diameter measurement method is proposed to analyze the image of the bearing cage size captured by the CCD camera. After image preprocessing, the threshold of the Sobel operator is changed and is used to detect the possible edge point set, after the effective circle detection, remove part of the interference point, and then using Zernike moment operator on the edge of these re-positioning to detect the image sub-pixel edge and calculate the exact location. Finally, these exact positions are fitted by using the least squares method to obtain the specific dimensions of the diameter of the cage. The actual operation shows that this method can achieve the expected accuracy, with good results and practical value. diameter measurement; bearing cages; Zernike moment; sub-pixel 2016-12-06; 2017-01-05。 孙建辉(1955-),男,浙江杭州人,教授级高工,硕士生导师,主要从事计算机控制和机电一体化航天非标地面测试设备研制方向的研究。 1671-4598(2017)05-0049-04 10.16526/j.cnki.11-4762/tp.2017.05.015 TP3 A3 实验及结果分析
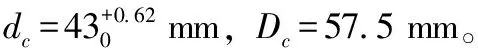




4 结论
