基于区间约束的谐波溯源方法

王智琦 ，杨洪耕，肖楚鹏 ，冷 月

（1.四川大学 电气信息学院，四川 成都 610065；2.南瑞（武汉）电气设备与工程能效测评中心，湖北 武汉 430074）

0 引言

电网中非线性负荷的不断接入以及电网中谐波源的复杂性和多变性，使谐波溯源成为谐波研究中的一个难点［1］。目前主要的谐波溯源方法分为两大类：一类是阻抗参数法，另一类是谐波功率方向法。

当采用“干预式”方法时，利用人为方式产生的附加扰动量计算系统侧谐波阻抗，得到的结果较可靠。但这种扰动很可能会对系统的正常运行产生不利影响，另外，在很多场合不存在可投切的电气元件和设备［2］。因此，工程上常采用“非干预式”方法，利用公共连接点（PCC）处谐波电压电流录波数据计算系统侧谐波阻抗。典型的方法有波动量法［2-3］、回归法［4-7］。这些方法有效的前提在于找到系统背景谐波不变的样本，在背景谐波波动较大时，计算结果往往不能满足工程精度的要求。随机独立矢量法［8-9］、独立分量法［10］、支持向量机［11］等方法在一定程度上消除了背景谐波波动的影响，但并无实质上的改变，当PCC处谐波主要不是用户侧谐波造成时，这类方法不能得到精确的计算结果［12］，尤其是阻抗角的精确值更难获得。由于电网中阻抗参数不易精确获得，而谐波功率方向是可直接根据测量数据得到的信息，所以工程上一直广泛采用更简单的谐波功率方向法。

文献［13］指出使用谐波有功功率方向法判断主谐波源位置具有局限性，该方法受PCC两侧谐波源相角差影响较大，不能保证谐波有功功率方向法始终适用。为此，文献［14］提出了基于无功功率方向判断主谐波源位置的方法，但该方法不仅与两侧等值谐波电压源幅值有关而且还与两侧谐波阻抗性质有关。当以两侧谐波电压源幅值大小为判断指标时，在两侧阻抗同呈感性的情况下仅能判断用户侧为主谐波源的情况，对于其他情况存在不确定性。且国内外尚无以谐波电压贡献作为考核指标时无功功率方向法的可行性研究。

由于阻抗参数法和谐波功率方向法均无法在任何情况下都具有较高的计算精度，除个别大型谐波源负荷工作人员能根据运行经验结合测量数据估计出主谐波源位置外，系统中还有许多PCC是由不同类型和容量的用电设备组成的，在这样的实际情况中，不能直接根据测量数据判断主谐波源位置。

针对上述问题，本文提出一种基于区间约束的谐波溯源方法。通过仿真分析得出无功功率方向法更适用于解决PCC处谐波溯源问题。以两侧谐波电压贡献度大小作为判断两侧谐波源作用大小的依据，根据两侧谐波电压贡献度随谐波电压电流夹角的变化规律，分区间推导得到判断系统侧和用户侧为主谐波源时各区间的严格不等式约束条件。本文以谐波无功功率方向法为基础，仅需根据谐波电压电流测量信息并结合简单的区间约束条件即可确定主谐波源。为提高溯源结果的可靠性，利用可信区间去除较严重的异常监测数据。通过多场景实际工程数据验证了本文方法的准确性和有效性。

1 谐波溯源方法及分析

1.1 谐波无功功率方向

谐波无功功率方向法的基本原理是通过测量PCC处谐波无功功率方向来追溯主谐波源。图1为两侧谐波源分析模型。图中，Iu、Ic分别为系统侧和用户侧等值谐波电流源；Zu、Zc分别为系统侧和用户侧等值谐波阻抗；以谐波电压Upcc作为参考相量，Upcc=Upcc∠0°，则谐波电流 Ipcc=Ipcc∠φ，φ 为谐波电压和电流的夹角。两侧谐波电流源幅值为Iu和Ic。可求出PCC处谐波无功功率为：

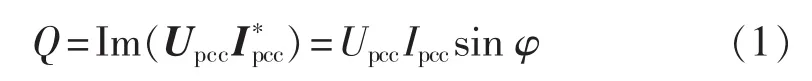
其中，Q为谐波无功功率。实际电网中，一般系统侧谐波阻抗呈感性，若Q>0，则用户侧为主谐波源；若Q<0，则系统侧为主谐波源。

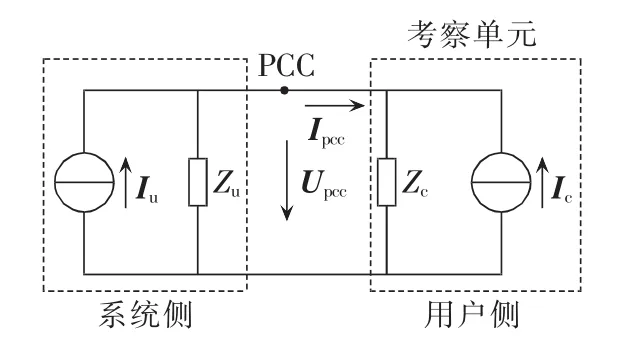
图1 谐波溯源模型Fig.1 Model of harmonic source tracing

1.2 谐波溯源分析

根据图1的谐波源模型，来用电压矢量叠加原理对PCC处谐波电压进行分解，得到系统和用户两侧在PCC处引起的谐波电压贡献度，进而判断主谐波源位置。比较两侧谐波电压贡献度大小的实质是比较两侧谐波电流源幅值的大小，即比较Iu和Ic大小。若用户侧谐波电流源幅值较大，则用户侧为主谐波源；反之，系统侧为主谐波源。

系统和用户两侧谐波源相位变化会影响PCC处谐波电压和电流的夹角φ，且实际情况下两者相位均可为任意角度，需分析夹角φ为任意值的情况。考虑实际电网运行中并以两侧阻抗同为感性的情况为例，利用表1参数［13］进行谐波溯源分析，其结果如图2所示。

表1 实验参数Table 1 Experiment parameters

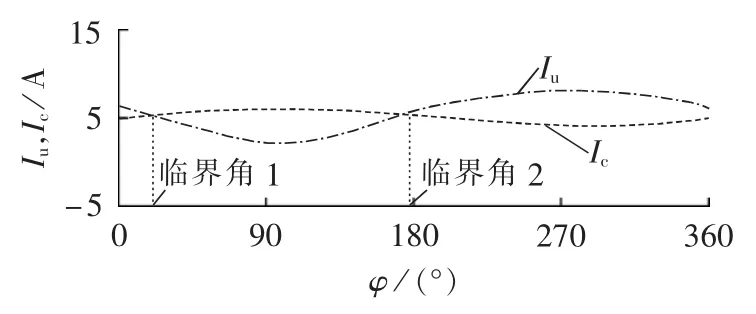
图2 谐波溯源分析Fig.2 Analysis of harmonic source tracing

根据图2仿真分析结果可知，利用谐波无功功率方向法判断用户侧为主谐波源的条件是夹角φ位于第一、二象限，系统侧为主谐波源的条件是夹角φ位于第三、四象限。而利用谐波电压贡献度法判断用户侧为主谐波源的条件是夹角φ位于两临界角之间，判断区域近似位于第一、二象限；判断系统侧为主谐波源的条件是夹角φ位于两临界角之外，判断区域近似位于第三、四象限。

虽然这2种方法的谐波溯源结果并不完全一致，但可认为谐波无功功率方向法在大部分情况下能准确判断主谐波源位置。相比有功功率方向法，利用谐波无功功率方向来判断主谐波源位置与谐波电压贡献度法的结果更准确。根据无功功率方向仅能初步估计主谐波源位置，要得到准确的谐波溯源结果，需在现有无功功率方向法的基础上附加一定约束条件。

2 基于区间约束的谐波溯源方法

2.1 谐波溯源方法的基础理论

根据谐波源等值模型，利用基尔霍夫电流定律得：

从而有：

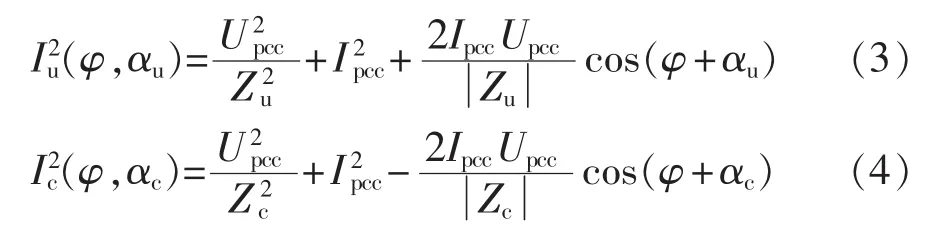
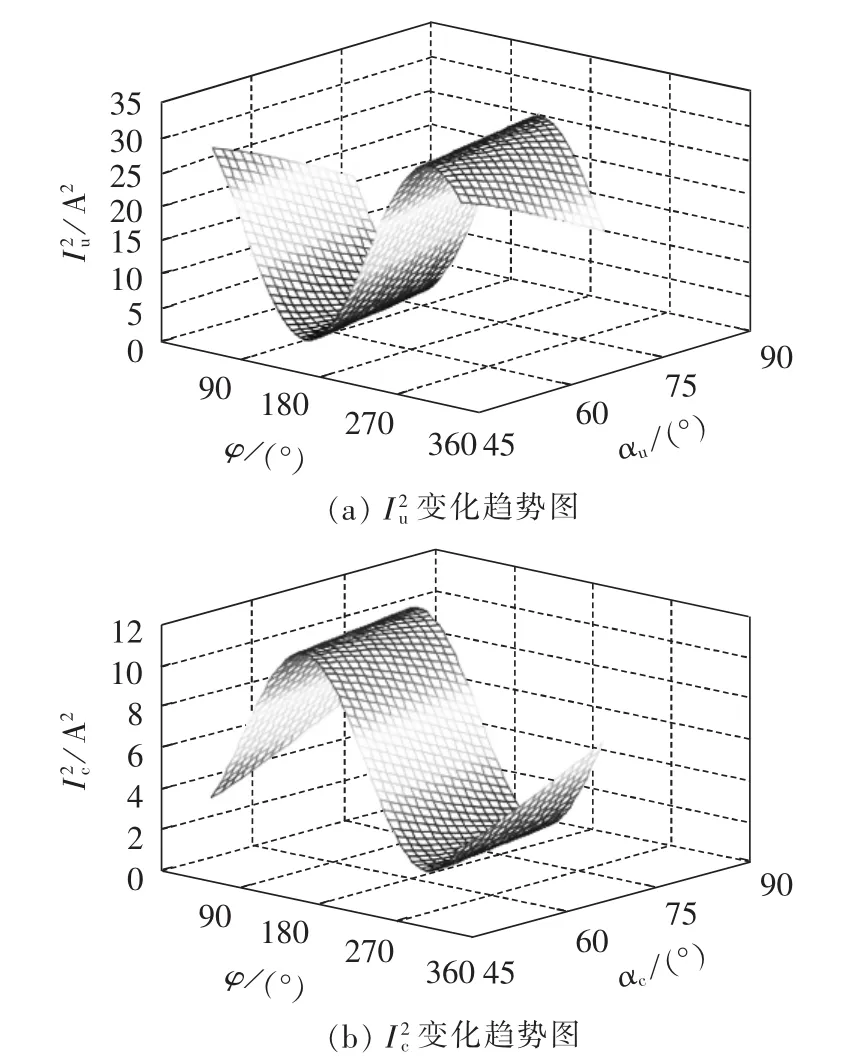
图3 谐波电压贡献度变化规律Fig.3 Variation rules of harmonic voltage contribution

其中，αu为系统侧阻抗角；αc为用户侧阻抗角。式（3）、（4）等号右侧的第一项、第二项构成恒定分量，第三项为波动分量。因为所以的恒定分量小于的恒定分量的波动分量幅值小于的波动分量幅值。若则系统侧为主谐波源；反之，用户侧为主谐波源。根据式（3）、（4）可得出两侧谐波贡献度与夹角φ阻抗角之间的变化关系，如图3所示。当阻抗角一定时的曲线随夹角φ呈正弦规律变化，而阻抗角变化时，曲线发生相移。

大多数情况下电网的系统侧和用户侧谐波阻抗均为感性；当无功补偿电容器选用电抗率为6%串联电抗器时，在5次以上谐波阻抗呈感性；在35 kV或10 kV的城市配电网中通常使用几千米的短电缆，仅在高次谐波（如29次以上［15］）处有可能会发生谐振，当谐波频率低于谐振点时用户侧谐波阻抗为容性。电网谐波阻抗具有一些固有特性，在一定条件下既可能呈感性，也可能呈容性，但多数条件下呈感性［12］。且系统阻抗与用户阻抗相对大小几乎是确定的。通常阻抗幅值的估计相比阻抗角的估计更为准确。

2.2 判断系统侧为主谐波源

根据谐波无功功率方向法，当系统侧谐波阻抗为感性时，若测得PCC处谐波无功功率方向为负，则系统侧为主谐波源，此时夹角φ位于第三、四象限。由于难以得到使恒成立的参数条件，需要根据不同阻抗性质及测量角度详细讨论并分类推导。

（1）两侧谐波阻抗同呈感性。

当两侧谐波阻抗角未知时，不能直接判断Iu和Ic的大小。的变化范围如图4所示的最大值、最小值分别为 Iumax、Iumin和 Icmax、Icmin。 对于测得的夹角φ，若任意阻抗角都使得Iumin>Icmax成立，则系统侧为主谐波源。

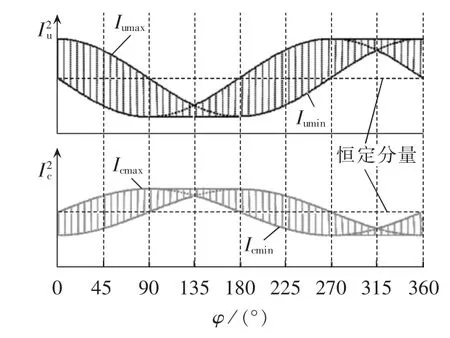
图4 两侧阻抗同呈感性时的趋势图Fig.4 Tendency chart when both sides are of inductive impedance

a.夹角φ位于第四象限。

因为的恒定分量大于的恒定分量，由图4可得的恒定分量的恒定分量>Icmax，由不等式的传递性可以得到Iumin>Icmax恒成立，即当夹角φ位于第四象限时，可直接判断系统侧为主谐波源。

b.夹角φ位于第三象限。

的最小值Iumin的表达式为：

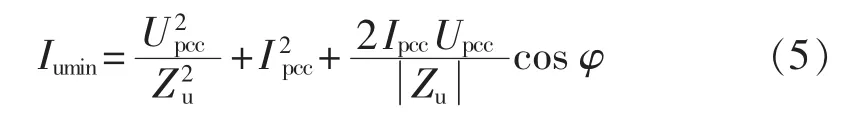
的最大值Icmax的表达式为：

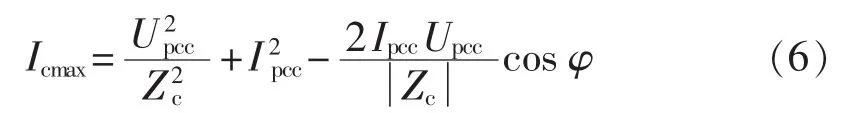
设的最小值大于的最大值，即Iumin>Icmax，可得：

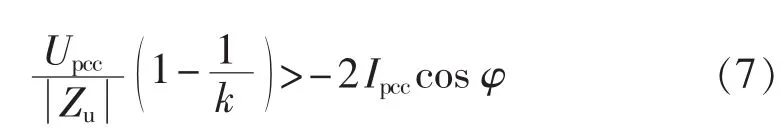
其中，两侧阻抗幅值的比值由式（7）可得：

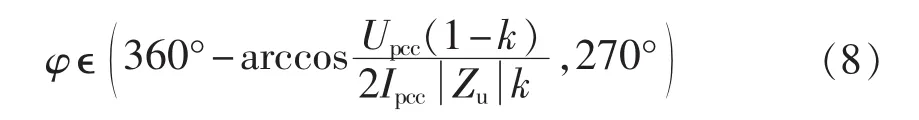
当夹角φ位于第三象限且满足式（8）范围时，可判断系统侧为主谐波源。

（2）Zu呈感性，Zc呈容性。

a.夹角 φ 位于第四象限（315°，360°）。

图5中，因为的恒定分量大于的恒定分量，且的波动分量幅值大于的波动分量幅值，所以Iumin>Icmax，可判断系统侧为主谐波源。

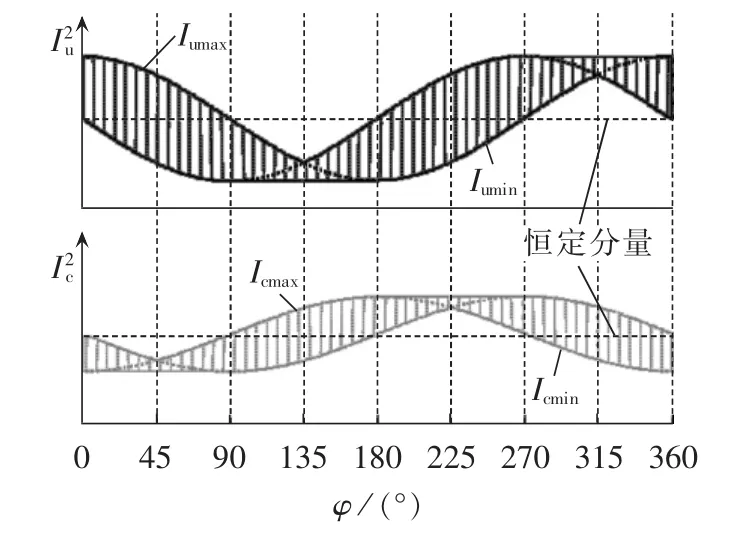
图5 系统侧阻抗呈感性、用户侧阻抗呈容性时的趋势图Fig.5 Tendency chart when system-side is of inductive impedance and customer-side is of capacitive impedance

b.夹角 φ 位于第四象限（270°，315°）。

的最小值Iumin的表达式为：

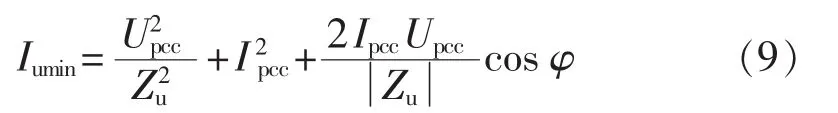
的最大值Icmax的表达式为：

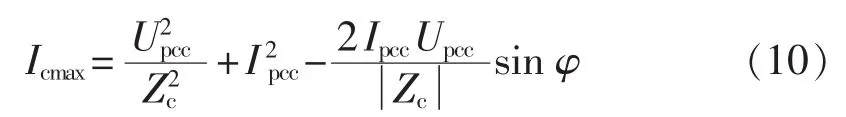
当满足式（11）时，可判断系统侧为主谐波源。

c.夹角φ位于第三象限。

的最小值Iumin的表达式为：

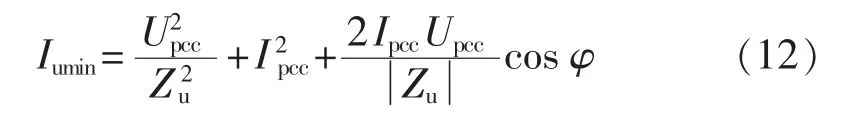
的最大值Icmax的表达式为：

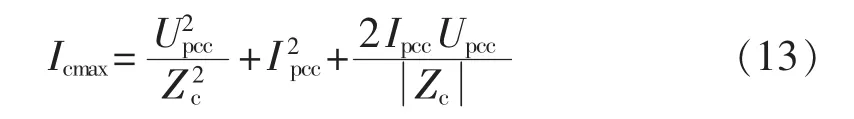
设的最小值大于的最大值，即Iumin>Icmax，简化后得：

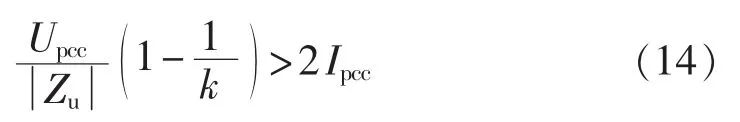
当满足式（14）时，可判断系统侧为主谐波源。

所以，当夹角φ位于第三、四象限时有如下结论。

a.两侧谐波阻抗同为感性时，当夹角φ位于第四象限时可直接判断系统侧为主谐波源；当夹角φ位于第三象限且满足式（8）范围时可判断系统侧为主谐波源。

b.Zu呈感性、Zc呈容性时，当夹角φ位于第四象限（315°，360°）时可直接判断系统侧为主谐波源；当夹角 φ 位于第四象限（270°，315°）且满足式（11）时可判断系统侧为主谐波源；当夹角φ位于第三象限且满足式（14）时可判断系统侧为主谐波源。

2.3 判断用户侧为主谐波源

同理，若测得PCC处谐波无功功率方向为正，则用户侧为主谐波源，此时夹角φ位于第一、二象限。推导过程与判断系统侧为主谐波源类似。

a.两侧谐波阻抗同为感性。

当夹角φ位于第二象限时，需满足区间约束：

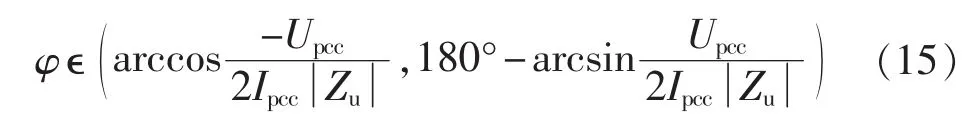
b.Zu呈感性，Zc呈容性。

当夹角 φ 位于第二象限（135°，180°）时，需满足区间约束：

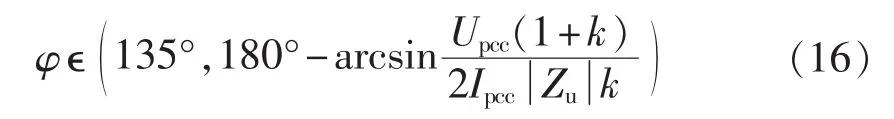
而其他更复杂情况不易得出区间约束公式，需根据谐波电压电流实测值及阻抗计算值通过式（2）判断Iu和Ic的大小，其难点在于如何获得两侧谐波阻抗幅值及阻抗角的准确值，其中阻抗角的准确值更难得到。相比回归法，独立分量法［10］、支持向量机［11］和极大似然估计法［16］的谐波阻抗计算结果较准确。可利用求出的阻抗估计值，并结合谐波电压电流测量信息进行谐波溯源。

当两侧谐波阻抗同呈容性时推导过程与两侧谐波阻抗同呈感性相似，所有区间边界值在180°处具有镜像对称性，且判断条件不变；同理，当Zu呈容性、Zc呈感性时，与Zu呈感性、Zc呈容性的判断关系在180°处具有镜像对称性。并将系统侧谐波阻抗呈感性时实际工程应用操作方法总结至表2中，当系统侧谐波阻抗呈容性、测得谐波电压电流夹角为φ时，可将其转换为系统侧谐波阻抗呈感性、谐波电压电流夹角为360°-φ的情况进行判断。

基于区间约束的谐波溯源方法采用严格不等式制约，其结果是利用谐波电压贡献度法求解的子集（充分条件），说明该方法的溯源结果一定正确。其研究范围涵盖了实际工程中所有情况，同时也证明了谐波无功功率方向法在区间约束下的有效性。

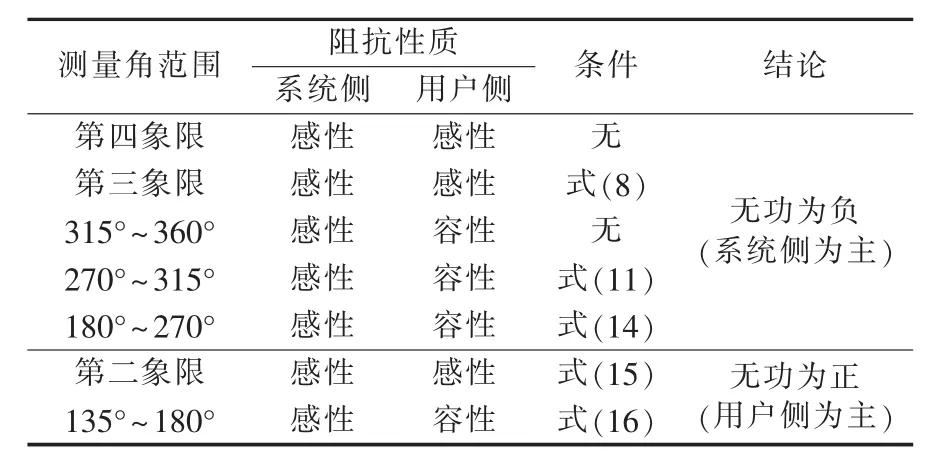
表2 方法归纳表Table 2 Summary table of harmonic source tracing

3 实例计算

3.1 算例1

实测数据来自法国一100 MV·A工业直流电弧炉的150 kV母线，系统短路容量为7500 Mvar。监测点系统侧为感性，用户侧是工业电弧炉负荷，为典型的感性负荷。使用LEM TOPAS 1000电能分析仪测量PCC处谐波电压和谐波电流，并通过快速傅里叶变换，获得每分钟谐波电压电流数据。以3次谐波测量值为例，如图6所示，图中为PCC处测得的某日连续10 h内的3次谐波电压、电流测量值，图7为测量数据散点图。由图6、7可知，在电弧炉工作时，即使谐波电压和电流的幅值波动较大，但其夹角始终在第二象限某范围内波动。

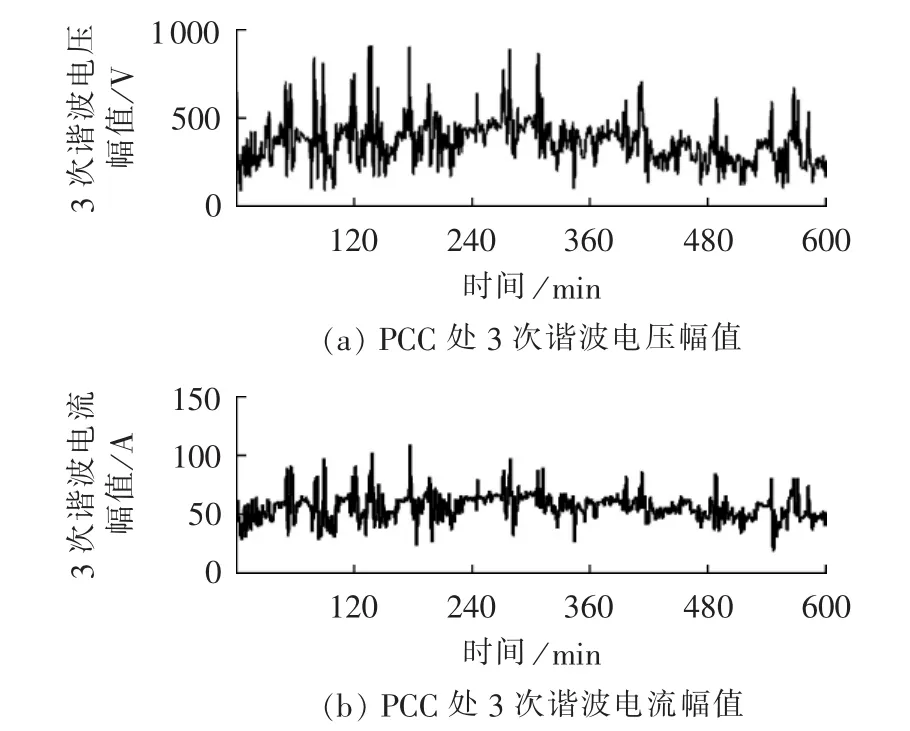
图6 PCC处3次谐波波形图Fig.6 3rd harmonic waveforms of PCC

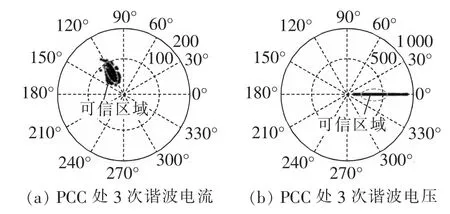
图7 3次谐波实测数据散点图Fig.7 Scatter plots of measured 3rd harmonic data

实际电网中，系统和用户两侧的谐波发射水平是实时变化的，准确有效的谐波溯源方法应在不引入大量异常数据的前提下将监测数据变化情况考虑在内。当监测数据混入异常数据后，会使计算结果失真。为避免上述情况，利用可信区间宽度来排除部分较严重的异常数据［17-18］。选取95%可信度水平，在确保正常数据保留的同时排除了对结果误差起主要作用的异常数据，即使剩余少量异常数据，其带来的误差可被大量正常数据削减，不会影响计算结果。

根据可信区间计算公式（17），求得谐波电压和谐波电流的可信区间。

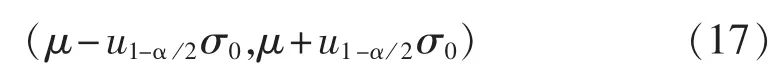
其中，μ为PCC处谐波电压和谐波电流的期望值；σ0为测量数据的标准差；α=0.05；u=1.96。去除异常边界值后，重新求得参数的期望值，如表3所示。

表3 PCC参数Table 3 Parameters of PCC

将表3参数代入式（15），可得φ的约束区间为（103°，167°），从图 7 可以看出，夹角 φ 主要在 120°附近波动，且其可信区间内的数据同样也位于约束区间内，由此可确定用户侧为主谐波源。

此外，利用本文方法还可以对每组实测数据及电力部门或用户比较关注的一些被污染较严重的时间区段进行谐波溯源分析，找出对PCC处谐波畸变产生主要作用的谐波源。

3.2 算例2

图8为我国某城市电网局部示意图，其直流落点及10 kV、35 kV负荷接入点的监测点信息见表4。监测点系统侧均为感性，由于城市电网大量使用电缆，以及装有大容量滤波装置，使10 kV、35 kV监测点的用户侧呈容性。直流落点的谐波影响，以及其谐波在电网中的交互影响、传导和放大等问题一直是工程实际遇到的问题和研究热点［12，19-20］。

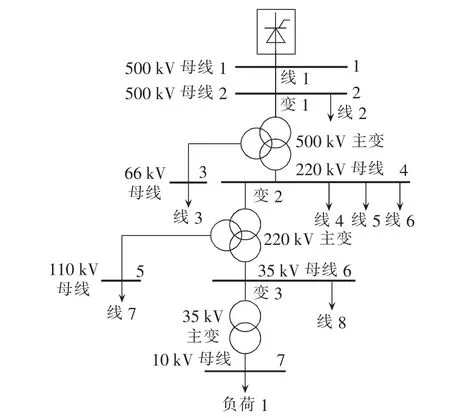
图8 具有直流落点的局部城市电网示意图Fig.8 Schematic diagram of partial urban power network with DC coupling point

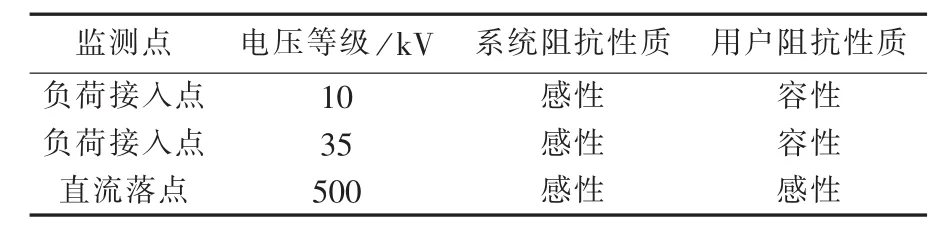
表4 监测点性质Table 4 Property of monitoring points

该城市电网中谐波主要来自直流落点和电网中其他非线性负荷。城市电网中直流落点作为系统侧谐波源从500 kV输电网向10 kV、35 kV配电网传播，用户侧非线性负荷作为谐波源从10 kV、35 kV配电网向500 kV输电网传播。分析城市电网中该10 kV、35 kV配电网及500 kV直流落点谐波的主要来源。

取某日负荷工作时10 kV监测点的连续1800 s谐波电压和电流监测数据，其11次谐波电压和电流监测数据如图9所示。电能质量监测平台1 s记录一组谐波数据，并对该监测数据做出散点图，如图10所示。此时，谐波电压电流夹角位于第四象限上半区域，可直接判断系统侧为该站的主谐波源。与10 kV监测数据的分析方法类似，文献［1］已经指出该城市电网35 kV监测点所监测的11次谐波的主谐波源同样位于系统侧。文献［12］使用Digsilent程序对整个城市电网进行计算，直流落点谐波电流传导至各支路的计算值占测量值的70%以上，可以确定谐波主要是由直流落点谐波在城市电网传导引起的。

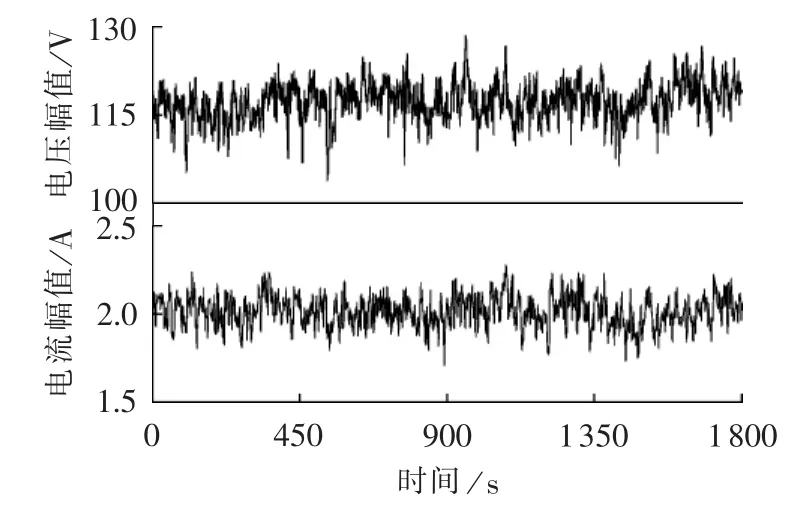
图9 11次谐波波形图Fig.9 11th harmonic waveforms

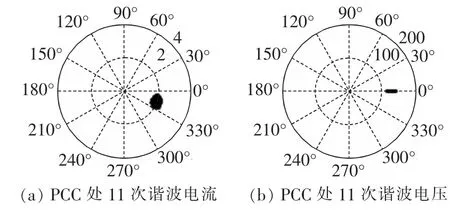
图10 负荷工作时监测数据散点图Fig.10 Scatter plots of monitored data when load is working

对500 kV直流落点处监测数据进行分析，如图11所示。可知该500 kV处的主谐波源也为系统侧。进一步确认了该城市电网中各支路谐波主要是由直流落点侧自上而下传递。

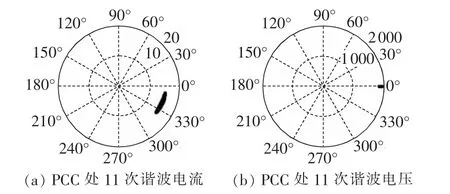
图11 谐波监测数据Fig.11 Monitored harmonic data

4 结论

a.分析了两侧谐波阻抗角为任意值时，谐波电压贡献度随谐波电压电流夹角的变化规律，得到基于区间约束的谐波溯源方法，其结果是谐波电压贡献度直接求解的充分条件，求得的溯源结果准确可靠。

b.区间约束法根据不同区间范围结合严格不等式制约，多数区间得出了不需要阻抗角参数的谐波溯源方法，部分区间得出了不需要阻抗幅值和阻抗角仅需谐波电压电流测量夹角的判断方法。

c.区间约束法研究范围涵盖了实际工程中的所有情况。利用多场景实际工程监测数据验证了谐波无功功率方向法在区间约束条件制约下的有效性，并给出实际工程应用的操作方法。

d.基于区间约束的谐波溯源方法为实现谐波责任划分及谐波经济管理奠定了基础，为解决供用电双方矛盾提供了理论依据。

参考文献：

［1］王智琦，杨洪耕，肖楚鹏，等.基于阻抗约束的谐波溯源方法［J］.电力系统自动化，2016，40（21）：182-188.WANG Zhiqi，YANG Honggeng，XIAO Chupeng，et al.Harmonic traceability method based on impedance constraints［J］.Automation of Electric Power Systems，2016，40（21）：182-188.

［2］惠锦，杨洪耕，叶茂清.基于阻抗归一化趋势判别的谐波发射水平评估［J］. 中国电机工程学报，2011，31（10）：73-80.HUIJin，YANG Honggeng，YE Maoqing.Assessing harmonic emission level based on the impedance gathering trend discrimination［J］.Proceedings of the CSEE，2011，31（10）：73-80.

［3］HUI J，FREITAS W，VIEIRA J C M，et al.Utility harmonic impedance measurement based on data selection［J］.IEEE Transactions on Power Delivery，2012，27（4）：2193-2202.

［4］张巍，杨洪耕.基于二元线性回归的谐波发射水平估计方法［J］.中国电机工程学报，2004，24（6）：50-53.ZHANG Wei，YANG Honggeng.A method for assessing harmonic emission level based on binary linear regression［J］.Proceedings of the CSEE，2004，24（6）：50-53.

［5］黄舜，徐永海.基于偏最小二乘回归的系统谐波阻抗与谐波发射水平的评估方法［J］. 中国电机工程学报，2007，27（1）：93-97.HUANG Shun，XU Yonghai.Assessing harmonic impedance and the harmonic emission levelbased on partialleast-squares regression method［J］.Proceedings of the CSEE，2007，27（1）：93-97.

［6］解绍锋.基于秩次回归的系统谐波阻抗分析与谐波评估方法［J］.电力自动化设备，2010，30（11）：29-33.XIE Shaofeng.Harmonic impedance analysis and harmonic assessment based on rank regression［J］.Electric Power Automation Equipment，2010，30（11）：29-33.

［7］孙媛媛，尹志明.基于M估计稳健回归的多谐波源责任区分［J］.中国电机工程学报，2012，32（31）：166-173.SUN Yuanyuan，YIN Zhiming.Quantifyingharmonicresponsibilitiesofmultiple harmonic sourcesbased on M-estimation robust regression［J］.Proceedings of the CSEE，2012，32（31）：166-173.

［8］HUI J，YANG H，LIN S，et al.Assessing utility harmonic impedance based on the covariance characteristic ofrandom vectors［J］.IEEE Transactions on Power Delivery，2010，25（3）：1778-1786.

［9］惠锦，杨洪耕，林顺富，等.基于独立随机矢量协方差特性的谐波发射水平评估方法［J］. 电力系统自动化，2009，33（7）：27-31.HUI Jin，YANG Honggeng，LIN Shunfu，et al.Assessment method of harmonic emission level based on covariance characteristic of random vectors［J］.Automation of Electric Power Systems，2009，33（7）：27-31.

［10］赵熙，杨洪耕.基于快速独立分量分析的系统侧谐波阻抗计算方法［J］. 电力系统自动化，2015，39（23）：139-144.ZHAO Xi，YANG Honggeng.Method of calculating system-side harmonic impedance based on FastICA［J］.Automation of Electric Power Systems，2015，39（23）：139-144.

［11］邱思语，杨洪耕.改进的加权支持向量机回归的谐波发射水平估计方法［J］. 电工技术学报，2016，31（5）：85-90.QIU Siyu，YANG Honggeng.Assessment method of harmonic emission level based on the improved weighted support vector machine regression［J］.Transactions of China Electrotechnical Society，2016，31（5）：85-90.

［12］陈甜甜，胡蓉，金祖洋，等.邻近直流输电落点的城市电网谐波传导特性分析［J］. 电网技术，2015，39（10）：3000-3004.CHEN Tiantian，HU Rong，JIN Zuyang，et al.Analysis research on harmonic transmission characteristics of urban power network adjacent to UHVDC terminal location［J］.Power System Technology，2015，39（10）：3000-3004.

［13］XU W，LIU X，LIU Y.An investigation on the validity of power-direction method for harmonic source determination ［J］.IEEE Transactions on Power Delivery，2003，18（1）：214-219.

［14］LI C，XU W，TAYJASANANT T.A “critical impedance”-based method for identifying harmonic sources［J］.IEEE Transactions on Power Delivery，2004，19（2）：671-678.

［15］陈海需，杨文焕，李荣高.电缆分布电容引起的港口供配电系统谐波谐振分析［J］. 电力科学与工程，2014，30（1）：38-41.CHEN Haixu，YANG Wenhuan，LI Ronggao.The analysis of harmonic resonance on distributed capacitance of power cable in harbor power distribution system［J］.Electric Power Science and Engineering，2014，30（1）：38-41.

［16］华回春，贾秀芳，曹东升，等.系统谐波阻抗估计的极大似然估计方法［J］. 中国电机工程学报，2014，34（10）：1692-1699.HUA Huichun，JIA Xiufang，CAO Dongsheng，et al.A maximum likelihood method for harmonic impedance estimation［J］.Proceedings of the CSEE，2014，34（10）：1692-1699.

［17］刘兴杰，谢春雨.基于贝塔分布的风电功率波动区间估计［J］.

（continued on page 165）（continued from page 160）电力自动化设备，2014，34（12）：26-30.LIU Xingjie，XIE Chunyu.Wind power fluctuation interval estimation based on beta distribution［J］.Electric Power Automation Equipment，2014，34（12）：26-30.

［18］吕晓禄，梁军，贠志皓，等.风电场出力的纵向时刻概率分布特性［J］. 电力自动化设备，2014，34（5）：40-45.LÜ Xiaolu，LIANG Jun，YUN Zhihao，et al.Longitudinal instant probability distribution of wind farm output power［J］.Electric Power Automation Equipment，2014，34（5）：40-45.

［19］杨光亮，邰能灵，郑晓冬，等.多馈入直流输电系统谐波交互影响分析［J］. 电力自动化设备，2016，36（1）：105-110.YANG Guangliang，TAI Nengling，ZHENG Xiaodong，et al.Harmonic interaction analysis formulti-infeed HVDC system［J］.Electric Power Automation Equipment，2016，36（1）：105-110.

［20］王灿，罗隆福，陈跃辉，等.一种改进型感应滤波高压直流输电系统及其谐波传递特性分析［J］. 电力自动化设备，2015，35（10）：127-132.WANG Can，LUO Longfu，CHEN Yuehui，et al.Harmonic interaction analysis for multi-infeed HVDC system［J］.Electric Power Automation Equipment，2015，35（10）：127-132.