戴维南等值参数时域仿真跟踪算法分析与改进

赵建伟 ，严 正 ，徐潇源 ，冯 楠 ，崔 勇 ，曹 路 ，李建华

（1.上海交通大学 电气工程系 电力传输与功率变换控制教育部重点实验室，上海 200240；2.国网上海市电力公司电力科学研究院，上海 200437；3.华东电网有限公司，上海 200210）

0 引言

基于戴维南等值的电压稳定分析方法因其物理概念明确、模型简单、能极大地简化电网结构、清晰地表征电力系统的电压稳定性，而受到广泛关注［1-4］。应用戴维南等值进行电压稳定分析的前提是求取戴维南等值参数。但由于电力系统的时变特性，戴维南等值参数受系统网络拓扑、发电状况、无功源状况、负荷状况及故障扰动等诸多因素影响。如何对不断变化的戴维南等值参数进行跟踪估计就成了关键所在。

Vu K.和Begovic M.M.等人率先针对实际电网提出运用本地测量数据跟踪估计戴维南等值参数的方法［5］，具有里程碑式的意义。之后国内外学者又相继提出了多种戴维南等值参数跟踪算法［6-26］，主要可概括为以下3种。第1种是基于本地测量或潮流计算的算法：利用测量单元或潮流计算得到运行点及其邻域的多组数据，通过黑箱模型和最小二乘辨识方法计算一组戴维南等值参数。这种算法假设运行点邻域内系统的戴维南等值参数保持不变，可能出现参数漂移问题［16］。第 2 种是基于偏差校正［17-18］或全微分［19-20］的算法：针对参数漂移问题做出了改进，偏差校正是在戴维南等值参数计算结果的基础上进行修正，克服了等值参数恒定的假设；基于全微分的算法是利用节点功率方程对戴维南等值参数及母线电压取全微分联立形成方程组，再求解对应的差分方程组得到等值结果，同样考虑了相邻运行点之间等值参数的变化。第3种是基于时域仿真的算法［21-22］：将时域仿真中的每一个时间步都作为一个运行点，每个运行点根据时域仿真软件提供的系统参数和状态数据计算一组戴维南等值参数，从而实现对戴维南等值参数的实时跟踪。

从戴维南等值参数跟踪算法的发展情况来看，研究重点集中在2个方面。一是提高算法准确性，例如：如何避免参数漂移，如何考虑运行点邻域内等值参数的变化。针对这一方面的解决方法众多，但都没能从根本上解决多个运行点计算单一戴维南等值参数所带来的局限。二是扩大算法适用性。大多数算法的本质为静态方法，仅适用于稳态情况或变化缓慢的中长期过程。而对于电压稳定问题而言，更多关注大小扰动下系统的暂态电压稳定性。因此如何实现电力系统暂态过程中的实时戴维南等值，是需要克服的难题，也是当前研究的主要关注点［21-25］。

事实上，不论是算法的准确性还是适用性，其根本问题在于将线性电路的戴维南等值原理直接引入强非线性的电力系统中。不同时间断面的系统状态和等值参数都是不同的，导致了采用多个运行点数据求取单一戴维南等值参数的算法都存在类似的局限性。针对这一问题，文献［21-22］提出了基于时域仿真的戴维南等值参数跟踪算法，其出发点是基于单个时间断面进行戴维南等值参数的计算。从多时间断面到单时间断面，既可以有效避免参数漂移等问题，又能够基于实时测量数据或仿真数据实现对大小扰动下系统暂态过程中戴维南等值参数的跟踪，为暂态电压稳定性分析提供了一条有益的途径。这类算法目前仍被普遍认为是“没有基于任何假设前提的”以及“精确的”［20-21，26-27］。

本文在文献［21-22］的基础上对基于时域仿真的戴维南等值参数跟踪算法进行进一步研究，主要包含两方面内容：对现有2种不同算法做了详细的分析和比较，并分别进行了修正，使两者在物理含义、数学前提和计算结果三方面实现统一；在现有2种算法的基础上，提出了改进的戴维南等值参数时域仿真跟踪算法，提高了等值结果的准确性。本文旨在通过探讨基于时域仿真的戴维南等值参数跟踪算法的计算原理、物理本质和假设条件，明确这类算法的优势，寻找可能存在的问题及解决方案，并为后续研究提供启示和经验。

1 戴维南等值原理与时域仿真跟踪算法

1.1 戴维南等值原理与等阻抗模判据

实际电力系统中，在任意时间断面时刻t，从某一负荷节点向系统看进去，均可把系统等值成一个电压源经过一个阻抗向该负荷供电的两节点戴维南等值系统，如图 1 所示。 图中，Et，iThev、Zt，iThev分别为系统侧的戴维南等值电势和戴维南等值阻抗；Ut，i、It，iLoad、Zt，iLoad分别为负荷节点的电压相量、流过负荷的电流相量和负荷的等值阻抗。

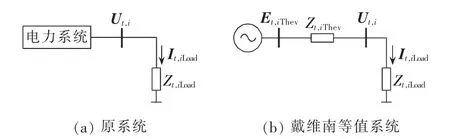
图1 戴维南等值原理Fig.1 Thevenin equivalent principle

为了保证戴维南等值电路准确有效，戴维南等值参数 Et，iThev和 Zt，iThev需要满足的条件为：使得负荷在戴维南等值系统中的状态与在实际系统中的状态完全相同，即 Ut，i、It，iLoad、Zt，iLoad均时刻保持一致，这也是计算戴维南等值参数的基础和目标。

一种普遍的观点认为：电力系统中的电压失稳源自负荷的功率需求超过系统传输功率极限，因此将系统进行面向负荷的戴维南等值后，可通过判断负荷功率和传输功率极限间的关系来确定系统是否电压稳定。在戴维南等值参数准确有效的前提下，图1（b）所示戴维南等值系统的电压稳定性可用等阻抗模判据进行判断，即负荷等值阻抗的模与系统戴维南等值阻抗的模相等时，系统运行于电压稳定临界点。这种方法已被广泛认同和采用。

1.2 戴维南等值参数时域仿真跟踪算法简介

基于时域仿真的戴维南等值参数跟踪算法的主要思想是：每一个仿真步都根据电网和仿真数据计算一次戴维南等值参数，从而实现对系统暂态过程中戴维南等值参数的跟踪。目前主要有2种实现算法，分别由文献［21］和［22］提出，两者基于同一出发点，即在电力系统暂态过程中的任一时刻t，时域仿真软件都要通过求解式（1）以获得节点电压向量。

其中，Y为系统导纳矩阵；Ut和It分别为t时刻系统节点电压向量和注入电流向量。

文献［21］的计算思路为：令 It0=［0，…，1，…，0］T（第 i个元素为 1，其余为 0），求解式（1）得到等值节点 i的综合阻抗 ZiT=Ut0，i（Ut0，i为只在节点 i处注入单位电流时节点i的电压变化量）；然后按图2所示补偿法以及 ΔUt，i=ZiTΔIt，i的关系，分别得到戴维南等值电路的开路电压和短路电流，从而求得戴维南等值参数，最终计算式为式（2），推导思路参见文献［21］。考虑到系统中其余负荷对等值参数的影响，该算法要求在每个时刻t都先将除等值节点i以外其余各负荷的等值导纳归并到导纳矩阵Y中（Yjj=Yjj+1 ／Zt，jLoad），然后再计算 ZiT以及戴维南等值参数。

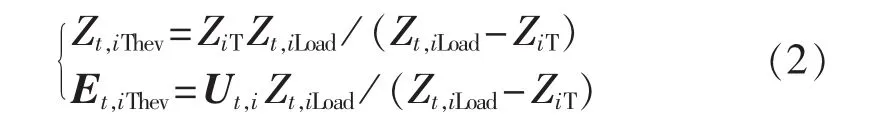
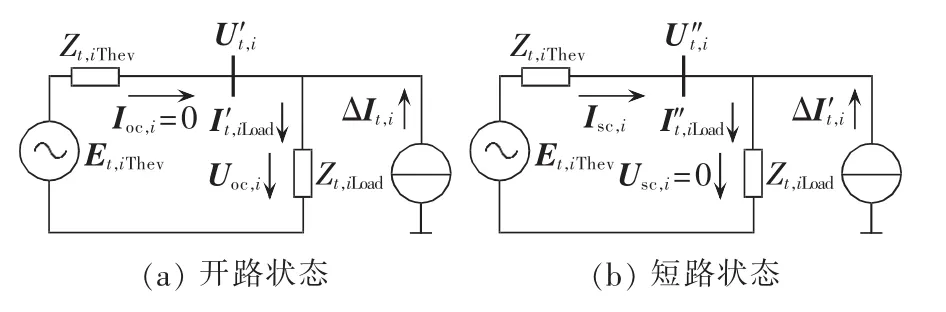
图2 补偿法戴维南等值电路Fig.2 Thevenin equivalent circuits of compensation method

文献［22］的思路是将等值节点i的电压设为0，求解式（1）得到节点 i短路时的电压向量［Ut0，1，…，0，…，Ut0，n］T（第 i个元素为 0），然后计算短路电流：

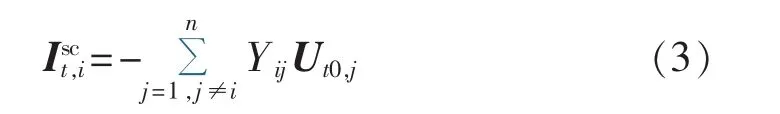
其中，n为系统节点数；负号表示流出，与节点注入电流反向。

图3为短路法求取戴维南等值参数等效电路图，把虚线左边电路看作整体，根据开路电压（即节点电压 Ut，i）和短路电流可先求得包含等值节点 i负荷阻抗的戴维南等值参数为：

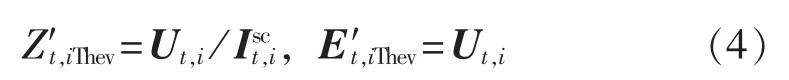
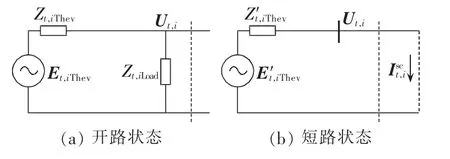
图3 短路法戴维南等值电路Fig.3 Thevenin equivalent circuits of short circuit method

再由图 3（a）、3（b）虚线左边电路的对应关系，可得不含等值节点i负荷阻抗的戴维南等值参数为：

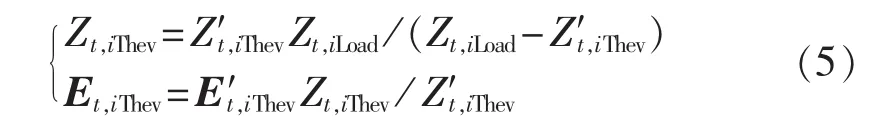
上述2种算法均以等值节点处的开路电压和短路电流为基础计算戴维南等值参数，只是具体实现方法不同。为了方便叙述和区分，下文统一将文献［21］和［22］所述算法分别称为补偿法和短路法。

2 现有2种算法的本质分析

2.1 2种算法的物理本质

电力系统暂态稳定计算中，多采用迭代法求解网络方程，每台发电机均可处理成诺顿等值电路［28-29］。其中，诺顿等值导纳只跟发电机本身参数有关（为常数），通常将其并入常规导纳矩阵Y中形成YT，以简化计算过程；而诺顿等值电流源严格意义上取决于发电机的（次）暂态电势、端节点电压和转子角，需要迭代才能求得，但忽略凸极效应时可认为近似不变。

根据补偿法和短路法的推导过程，2种算法均要求发电机节点的注入电流在系统状态发生变化（在等值节点处注入单位电流或将等值节点负荷短路）时保持不变。因此，两者都将潮流网络方程YU=I中的导纳矩阵Y替换成稳定计算中的导纳矩阵YT，这样便可将发电机节点的注入电流转化成对应的诺顿等值电流源电流，在假设各发电机的诺顿等值电流源保持不变的前提下，算法能够成立。

补偿法和短路法均通过分别求取等值节点处的开路电压和短路电流，再间接计算戴维南等值参数。

对于补偿法而言，其求解开路电压和短路电流的本质是应用叠加原理，将开路或短路时的系统状态看作是2种情况的叠加：一是正常运行时的情况；二是将系统中各发电机的电势均置0，仅在等值节点处加一个电流源的情况，后者与ZiT密切相关。观察发现，补偿法求取ZiT的思路与采用导纳矩阵计算三相对称短路电流的方法完全一致［29］，ZiT正好等同于短路电流计算中，将所有发电机诺顿等值电流源开路后故障分量网络中等值节点的自阻抗。

对于短路法而言，其求解短路电流的方法是三相对称短路电流的求法，也是2种情况的叠加：一是正常运行时的情况；二是将系统中各发电机节点的注入电流（诺顿等值电流源）置0，仅在等值节点处加一个电压源（与原电压反向）的情况。因此该方法计算所得戴维南等值参数同样取决于故障分量网络。

综上所述，现有2种算法的本质都是根据故障分量网络与叠加原理求解戴维南等值参数，即两者的物理意义是统一的。

2.2 2种算法的数学解析

对于含有m台发电机、n个节点的系统，将发电机节点单独列写，式（1）可写成如下形式：

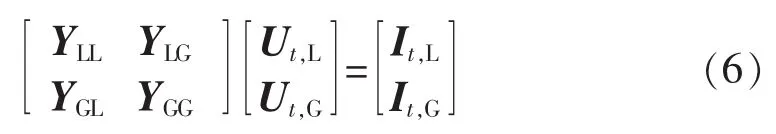
其中，YLL、YLG、YGL、YGG为 Y 的子矩阵；Ut，L、It，L分别为所有负荷节点（包括无负荷联络节点）的电压向量、注入电流向量；Ut，G、It，G分别为所有发电机节点的电压向量、注入电流向量。

易知YGG可逆，因此可将式（6）展开并推导得到：

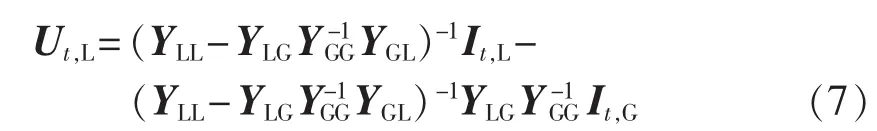
令式（7）可简写成：

取等值节点i对应的方程有：

其中，It，i为等值节 点的注入电流；It，Gj、It，Lj分 别 为除等值节点外其他发电机节点、负荷节点的注入电流。

理论上式（9）恒成立，这里对2种算法的数学假设进行分析。

对补偿法而言，一方面由于矩阵K、H均为常数矩阵，则在用电流源进行补偿后，存在如下关系式：

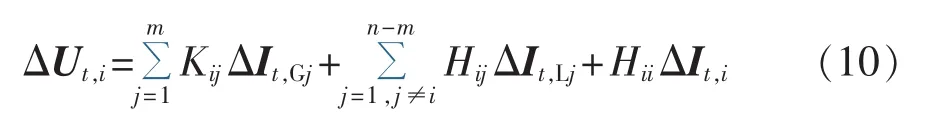
其中，ΔIt，Gj、ΔIt，Lj、ΔIt，i表示相应注入电流的变化量。

另一方面，根据分解矩阵求逆法和分块矩阵求逆法［30］可以证明，H 是 Y-1左上角的（n-m）×（n-m）阶子矩阵，从而有Hii=ZiT。

因此补偿法中采用关系式 ΔUt，i=ZiTΔIt，i推导计算戴维南等值参数，其隐含前提为：

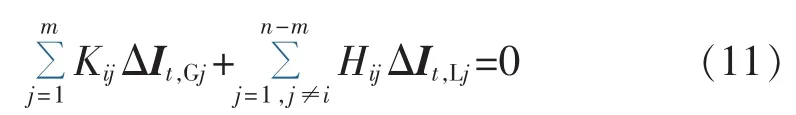
对短路法而言，由于令 Ut，i=0，根据式（9）有：

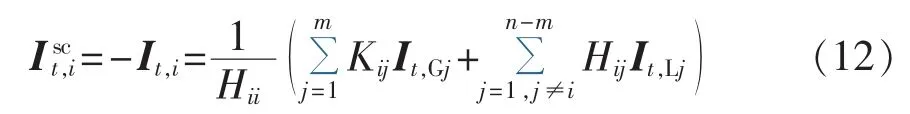
式（12）本质上与式（3）相同，其隐含条件是要求在令 Ut，i=0 前后保持不变，即也要满足式（11）。

综上所述，从数学层面来看，现有2种算法所需满足的条件也是一致的。

3 对现有时域仿真跟踪算法的改进

3.1 现有2种算法的修正和统一

由第2节分析可知，补偿法和短路法的物理本质和数学前提是一致的。两者都将导纳矩阵Y替换成YT，并认为发电机的诺顿等值电流源恒定不变，以满足式（11）等号左边第一项为0的假设。但两者对各个负荷节点的处理方式有所区别。

a.补偿法在计算综合阻抗之前，先将除等值节点以外其余各负荷的等值导纳归并到导纳矩阵中，相当于将负荷节点转换成无负荷联络节点（注入电流恒为0），从而使式（11）等号左边的第二项也为0。不过该方法忽略了一点：式（10）中的 ΔIt，i为等值节点处注入电流的变化量，而采用图2所示补偿法时，等值节点处注入电流不等于补偿电流源电流，还需要考虑流过负荷自身的电流的影响。

b.短路法先求取包含等值节点负荷阻抗的戴维南等值参数，再间接计算不包含等值节点负荷阻抗的戴维南等值参数，相当于考虑了等值节点处负荷自身对戴维南等值参数的影响。但该方法未考虑其余负荷节点，即未使式（11）等号左边的第二项为0。

因此2种算法均未全面地对系统中的所有负荷进行处理，以满足式（11）的数学假设，从而消除其对戴维南等值参数的影响。分别对两者做如下修正。

a.对于补偿法而言，在计算综合阻抗之前，将等值节点处的负荷同其他负荷一样处理，从而保证补偿法使用过程中，补偿电流源的电流就等于节点注入电流。具体做法是每次计算ZiT之前都先将等值节点处的负荷阻抗转换成导纳归并到导纳矩阵YT的相应对角元素（YTii=YTii+1 ／Zt，iLoad）。

b.对于短路法而言，计算短路电流之前，将等值节点以外所有负荷节点都转换成无负荷联络节点，从而保证计算过程中其余负荷不会对等值结果产生影响。具体做法是每次计算Isct，i之前都先将等值节点以外其余各负荷的等值导纳归并到导纳矩阵YT的相应对角元素中（YTjj=YTjj+1 ／Zt，jLoad）。

经过以上修正，理论上对于同一个电力系统而言，2种算法的计算结果肯定是一致的。

3.2 改进的戴维南等值参数时域仿真跟踪算法

现有2种基于时域仿真的戴维南等值参数跟踪算法的出发点都是试图基于单时间断面对系统进行戴维南等值，但本质仍然都是“两状态法”，即通过假想开路和短路2种状态来求取戴维南等值阻抗，且还需假设系统中发电机和负荷节点的状态始终保持不变（即式（11）成立）。这个做法类似于线性化，当开路和短路这2种状态离当前运行点不远时，可以得到相对合理的等值结果，但是当开路状态或短路状态过于偏离当前运行点时，就可能引起较大误差。

换个角度而言，式（9）理论上在系统任何状态、任何时刻下均成立。如果∑KijIt，Gj+∑HijIt，Lj不会因It，i变化而变化，那么对照图1所示的戴维南等值系统，∑KijIt，Gj+∑HijIt，Lj即为戴维南等值电势，Hii即为戴维南等值阻抗。而实际运行中，由于电力系统的非线性，∑KijIt，Gj+∑HijIt，Lj一般都会随 It，i变化而变化，这就是此类算法的误差根源。文献［21］和［22］算法分别对发电机和负荷进行了统一处理，使得式（11）的假设条件近似得到满足，但其精度仍存在一定提升空间。

基于以上讨论，为了尽量减小可能出现的误差，从式（9）和式（11）出发，结合常用的综合负荷模型，提出改进的戴维南等值参数时域仿真跟踪算法，具体步骤如下。

a.将发电机参考节点的等值导纳设为无穷大。相当于使故障分量网络中的对应节点接地，从而保证该节点电压在系统状态变化前后近似保持不变，更符合实际且满足式（11）中 ΔIt，Gj=0 的假设。

b.将其余发电机节点仍用诺顿等值电路进行处理，并将等值电流源看作恒定。

c.将系统中所有恒阻抗负荷节点的等值导纳归并到导纳矩阵中。相当于将恒阻抗负荷节点变成无负荷联络节点，从而满足式（11）中对应 ΔIt，Lj=0的假设。

d.将系统中所有恒电流负荷节点的注入电流保留在YUt=It的右边。这是因为恒电流负荷本身就满足式（11）中 ΔIt，Lj=0 的要求。

e.将系统中所有恒功率负荷和感应电动机负荷当作恒阻抗负荷，同步骤c一样进行处理。感应电动机负荷可以这么处理的原因在于，在某一时刻，其等值阻抗由转差率决定，而转差率不会突变。

以上改进算法的具体实现过程为：将网络方程YUt=It中导纳矩阵Y替换成YT；将参考节点对应的方程去除，把与参考节点电压有关的项移到等式右边；对各类负荷进行处理，修改导纳矩阵得到Y′T；对方程进行变换。这样式（1）可变形为：

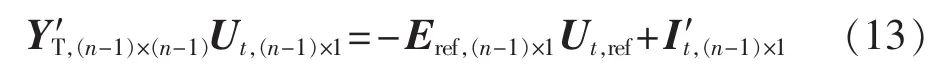
其中，Ut，ref为参考节点电压；Eref，（n-1）×1为 YT中参考节点对应的列向量；上标“′”表示负荷处理后的矩阵或向量；n-1为去掉参考节点对应行或列后的维数。

对式（13）进行变换后，有：

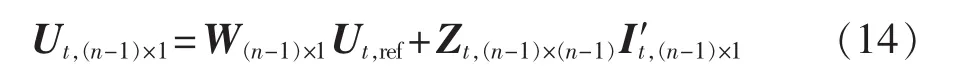
其中取等值节点 i对应的方程，并将其注入电流替换成负荷电流 It，iLoad，得到：

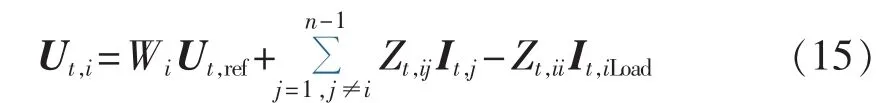
其中，等式右边第二项中的It，j仅包含恒电流负荷节点的注入电流，以及除参考节点外发电机的诺顿等值电流源电流，因此在任意时间断面时刻t，WiUt，ref+∑Zt，ijIt，j近似为与 It，iLoad无关的量，根据图 1（b）所示戴维南等值电路，可得改进算法的计算公式为：

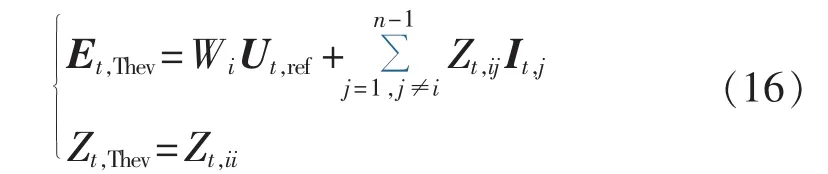
改进算法流程图如图4所示。

4 算例分析

4.1 修正方案的效果验证

为了验证对现有2种算法修正后的效果，对缓慢增长的稳态情况（稳态可看作是一种特殊的暂态过程）进行测试。测试系统为图5所示的IEEE 9节点系统，以恒定功率因数逐步增加负荷节点C的有功、无功功率，其余负荷的功率和发电机的有功出力均保持不变，直到潮流不再收敛。在负荷节点C处进行戴维南等值，等值结果如图6所示，其中λ为负荷节点C的增长倍数，纵轴数据为标幺值，后同。

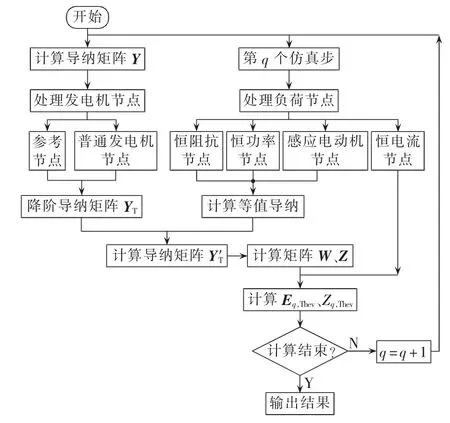
图4 改进算法流程图Fig.4 Flowchart of improved algorithm

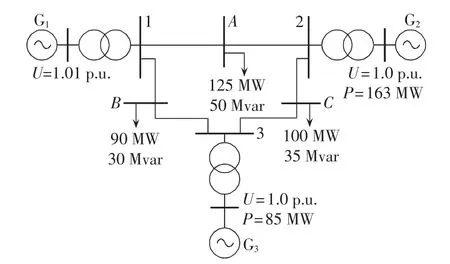
图5 IEEE 9节点测试系统Fig.5 IEEE 9-bus test system

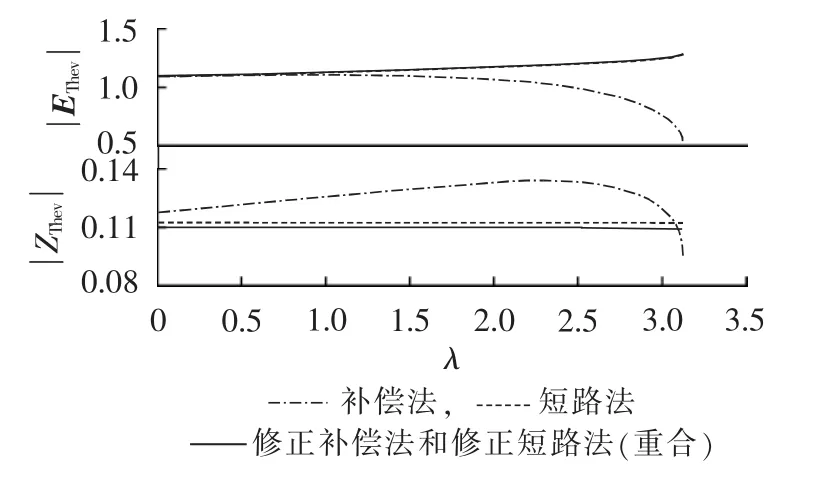
图6 戴维南等值结果Fig.6 Results of Thevenin equivalent parameter tracking

图6结果显示，在未修正算法之前，现有2种基于时域仿真的戴维南等值参数跟踪算法的计算结果有很大差异，特别是在等值节点处重负荷的时候更加明显。经过修正之后，2种算法的结果完全相同，验证了两者的统一性。

4.2 改进算法的效果验证

4.2.1 稳态算例

（1）单机单负荷。

仍以图5所示系统为例，只保留发电机G1和负荷C。负荷C以恒定功率因数增长，直到潮流不再收敛。分别采用现有算法和改进算法对负荷节点C进行等值，结果如图7所示，因为戴维南等值电势可根据戴维南等值阻抗求得，所以这里只验证戴维南等值阻抗的准确性，后同。

图7 改进算法和现有算法等值结果比较Fig.7 Comparison of equivalent impedance between improved algorithm and existing algorithm

图7结果表明，在系统功率传输极限点处，改进算法的等值结果满足等阻抗模判据的要求，说明针对参考节点的改进算法是正确的。

（2）单机三负荷。

在图5所示系统的基础上，去掉发电机G2和G3，将所有负荷的功率减半。负荷A和负荷B采用如下3种组合：①恒阻抗负荷；②恒电流负荷；③50%恒阻抗+50%恒电流负荷。在负荷A、B组合方式确定的情况下，设定负荷C以恒定功率因数增长，直到潮流不再收敛。计算考虑ZIP负荷模型的系统潮流，并分别用现有算法和改进算法对负荷节点C进行等值，得到结果如表1所示（这里只关注功率传输极限点），表中电阻、电抗、阻抗数据均为标幺值。

由表1结果可知，除等值节点以外其余负荷为恒电流负荷和恒阻抗负荷的任意组合时，改进算法均能准确计算功率传输极限点，其精度远高于现有算法。这也说明改进算法对恒阻抗负荷和恒电流负荷的处理是正确的。

4.2.2 暂态算例

在图5所示系统基础上将负荷C的功率增加为原来的3倍进行初始潮流计算，设定系统中负荷A和负荷B均为恒功率负荷，负荷C为感应电动机负荷。母线3在0.2 s时刻发生三相短路故障，根据不同的故障清除时刻，分别进行暂态仿真和戴维南等值（节点 C）。

（1）13.8869个周期清除故障。

在该情形下，系统处于临界电压稳定状态，暂态仿真和戴维南等值结果如图8所示。根据图8，按照等阻抗模判据可知，现有算法的计算结果显示系统电压失稳，而改进算法的计算结果始终小于可判断系统电压稳定，后者符合实际情况，即改进算法的等值结果更为准确。

表1 功率传输极限点处改进算法和现有算法等值结果比较Table 1 Comparison of equivalent parameters at power transmission limit point between improved algorithm and existing algorithm

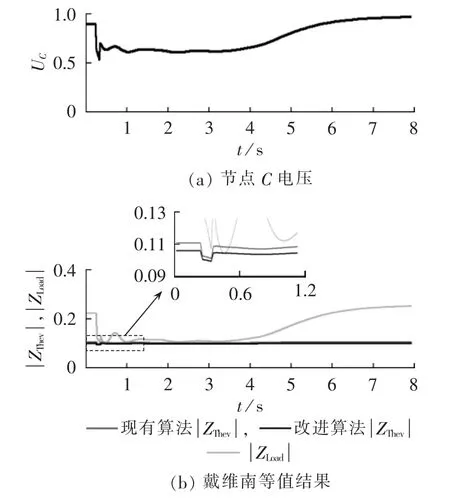
图8 暂态仿真和戴维南等值结果1Fig.8 Results of transient simulation and Thevenin equivalent parameter tracking（case 1）

（2）13.8870个周期清除故障。

在该情形下，系统处于临界电压失稳状态，暂态仿真和戴维南等值结果如图9所示。由图9可知，现有算法和改进算法结果均显示系统发生电压失稳，但现有算法判断系统发生电压失稳的时刻约为0.45 s，过于保守，而改进算法判断系统发生电压失稳的时刻约为3.3 s，比较符合实际情况。

（3）13.8900个周期清除故障。

在该情形下，系统发生电压失稳，暂态仿真和戴维南等值结果如图10所示。图10表明，改进算法的计算结果也并非完全准确，和现有算法一样也会出现误判，这是由于处理普通发电机节点和恒功率负荷时仍做了一定程度的假设和近似。

综上所述，改进算法等值结果的精度相较于现有算法有所提高，能更加准确地对电压稳定性进行判断。但由于改进算法也没有从根本上摆脱用网络方程和“两状态法”计算戴维南等值参数的思路和框架，无法很好地处理非线性带来的误差，所以仍然存在一定的局限性。

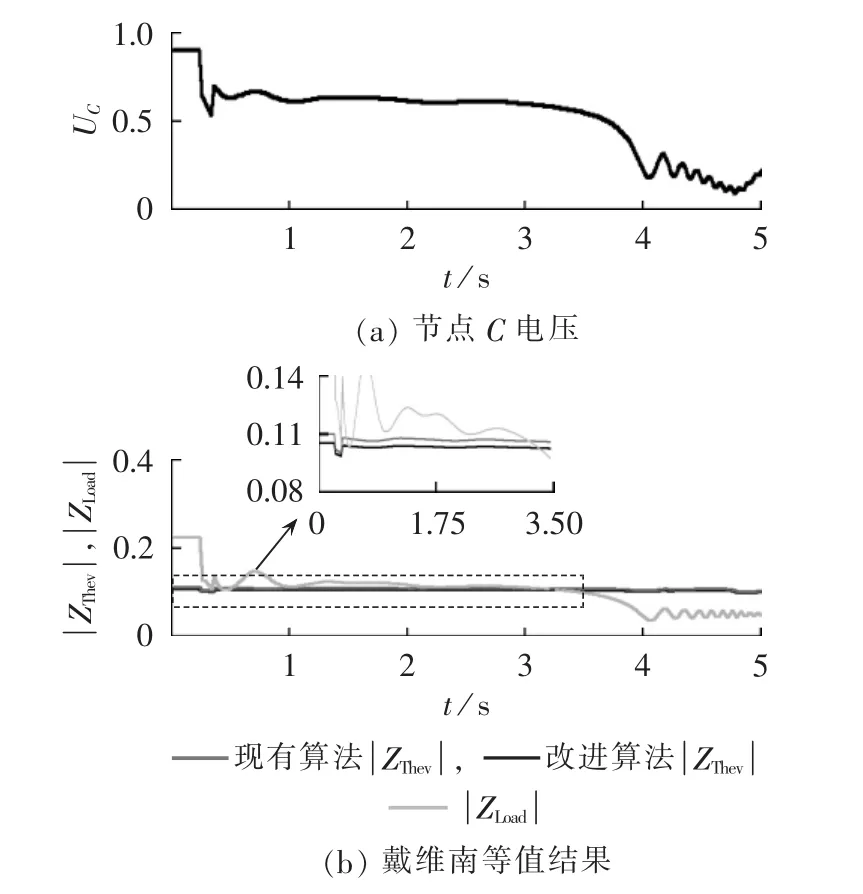
图9 暂态仿真和戴维南等值结果2Fig.9 Results of transient simulation and Thevenin equivalent parameter tracking（case 2）

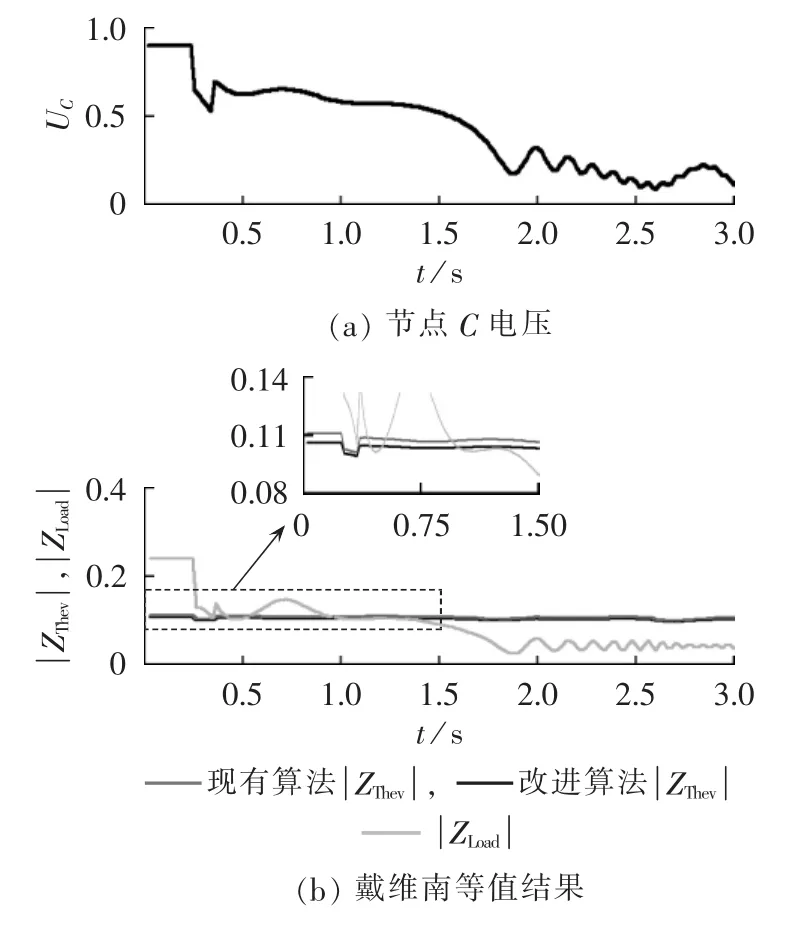
图10 暂态仿真和戴维南等值结果3Fig.10 Results of transient simulation and Thevenin equivalent parameter tracking（case 3）

5 结论

系统结构和负荷特性日益复杂的形势下，电力系统在大小扰动下的暂态电压稳定性对于其安全运行至关重要。基于时域仿真的戴维南等值参数跟踪算法提供了一种用单时间断面数据进行戴维南等值的视角，可实现对戴维南等值参数的实时跟踪，从而用于暂态电压稳定分析，这种探索是有益的，且有着较高理论研究价值和一定的实用意义。

现有的2种基时域仿真的戴维南等值参数跟踪算法（补偿法和短路法）在物理意义、数学前提和计算结果三方面均具有统一性，但它们的本质仍然是基于短路、开路2种状态来求解戴维南等值参数。采用这种“两状态法”原理简单、计算方便、易于实现，其不足在于所得结果可能与实际存在偏差。本文基于现有算法提出了改进方案，可以提高等值结果的准确性，但也没能从根本上突破“两状态法”的局限。因此，这也为后续研究工作提供了启示：如何跳出现有算法的框架，抛弃线性电路的相关方法和结论，考虑电力系统的非线性，真正基于单一时间断面进行戴维南等值，可作为今后的一个研究方向。

此外，从算法本身而言，基于时域仿真的戴维南等值参数跟踪算法（现有算法和改进算法）并不一定要依赖于时域仿真软件。但作为一类需要全网网络数据和电压、电流实时数据的算法，时域仿真软件提供了一个很好的平台，也是当前最易实现的方案。基于时域仿真，可将此类算法应用于研究电力系统暂态电压稳定性与戴维南等值参数的关系与机理，离线识别电力系统中暂态电压稳定薄弱节点等场景。在今后测量和通信条件成熟的情况下，这类算法也可以脱离时域仿真，应用于在线计算。

参考文献：

［1］KESSEL P，GLAVITSCH H.Estimating the voltage stability of a power system［J］.IEEE Transactions on Power Delivery，1986，1（3）：346-354.

［2］OHTSUKA K，YOKOKAWA S，TANAKA H，et al.An equivalent of multi-machine power systems and its identification for on-line application to decentralized stabilizers［J］.IEEE Transactions on Power Systems，1989，4（2）：687-693.

［3］CHEBBO A M，IRVING M R，STERLING M J H.Voltage collapse proximity indicator：behaviour and implications［J］.IEE Proceedings C-Generation，Transmission and Distribution，1992，139（3）：241-252.

［4］HAQUE M H.A fast method for determining the voltage stability limit of a power system［J］.Electric Power System Research，1995，32（1）：35-43.

［5］VU K，BEGOVIC M M，NOVOSEL D，et al.Use of local measurement to estimate voltage stability margin［J］.IEEE Transactions on Power Systems，1999，14（3）：1029-1035.

［6］FUSCO G，LOSI A，RUSSO M.Constrained least squares methods for parameter tracking of power system steady-state equivalent circuits［J］.IEEE Transactions on Power Delivery，2000，15（3）：1073-1080.

［7］MILOSEVIC B，BEGOVIC M.Voltage-stability protection and control using a wide-area network of phasor measurements［J］.IEEE Transactions on Power Systems，2003，18（1）：121-127.

［8］VERBIC G，GUBINA F.A new concept of voltage-collapse protection based on local phasors［J］.IEEE Transactions on Power Delivery，2004，19（2）：576-581.

［9］王漪，柳焯.基于戴维南等值的系统参数跟踪估计［J］.电网技术，2000，24（11）：28-30.WANG Yi，LIU Zhuo.Tracking and estimation of system parameter using Thevenin’s equivalent［J］.Power System Technology，2000，24（11）：28-30.

［10］王芝茗，王漪，徐敬有，等.关键负荷节点集合电网侧戴维南参数预估［J］.中国电机工程学报，2002，22（2）：16-20.WANG Zhiming，WANG Yi，XU Jingyou，et al.Prediction of Thevenin’s equivalent parameters on electrical power network side for the muster of key load nodes［J］.Proceedings of the CSEE，2002，22（2）：16-20.

［11］李娟，刘修宽，曹国臣，等.一种面向节点的电网等值参数跟踪估计方法的研究［J］.中国电机工程学报，2003，23（3）：30-33.LI Juan，LIU Xiukuan，CAO Guochen，et al.A tracking estimation method for network equivalent parameters of facing the node［J］.Proceedings of the CSEE，2003，23（3）：30-33.

［12］傅旭，王锡凡.电力系统静态电压稳定性在线监控（一）——一种可在线应用的计及负荷静态特性的电压稳定指标［J］.电力自动化设备，2005，25（8）：23-26.FU Xu，WANG Xifan.On-line voltage stability monitoring for electric power system part 1：on-line voltagestabilityindex considering load static characteristics［J］.Electric Power Automation Equipment，2005，25（8）：23-26.

［13］刘明松，张伯明，姚良忠，等.基于PMU和改进戴维南等值模型的电压稳定在线监视［J］.电力系统自动化，2009，33（10）：6-10.LIU Mingsong，ZHANG Boming，YAO Liangzhong，et al.On-line voltage stability monitoring based on PMU and improved Thevenin equivalent model［J］.Automation of Electric Power Systems，2009，33（10）：6-10.

［14］罗华伟，吴政球，戴庆华，等.电网戴维南等值参数的快速计算［J］.中国电机工程学报，2009，29（1）：35-39.LUO Huawei，WU Zhengqiu，DAI Qinghua，et al.Fast computation of Thevenin equivalent parameters［J］.Proceedings of the CSEE，2009，29（1）：35-39.

［15］郑飞平，刘宝柱.电压稳定临界参数的异步接替求取策略［J］.电力自动化设备，2011，31（3）：98-102.ZHENG Feiping，LIU Baozhu.Determination of voltage stability critical parameters by asynchronous succession strategy［J］.Electric Power Automation Equipment，2011，31（3）：98-102.

［16］李来福，于继来，柳焯.戴维南等值参数的漂移问题研究［J］.中国电机工程学报，2005，25（20）：1-5.LILaifu，YU Jilai，LIU Zhuo.Research on parametersdrift problem in tracking Thevenin equivalent［J］.Proceedings of the CSEE，2005，25（20）：1-5.

［17］CORSI S，TARANTO G.A real-time voltage instability identification algorithm based on local phasor measurements［J］.IEEE Transactions on Power Systems，2008，23（3）：1271-1279.

［18］牟善科，丁涛，顾伟，等.基于偏差校正的戴维南等值参数在线跟踪改进算法［J］.电力系统保护与控制，2011，39（2）：23-28.MOU Shanke，DING Tao，GU Wei，et al.An improved algorithm for on-line tracking Thevenin equivalent parameters based on deviation correction［J］.Power System Protection and Control，2011，39（2）：23-28.

［19］汤涌，孙华东，易俊，等.基于全微分的戴维南等值参数跟踪算法［J］.中国电机工程学报，2009，29（13）：48-53.TANG Yong，SUN Huadong，YI Jun，et al.Tracing algorithm for Thevenin equivalent parameters based on complete differential equation［J］.Proceedings of the CSEE，2009，29（13）：48-53.

［20］孙华东，陈树勇，常晓鹏，等.适应大扰动的电力系统戴维南等值参数跟踪算法［J］.中国电机工程学报，2012，32（22）：126-132.SUN Huadong，CHEN Shuyong，CHANG Xiaopeng，et al.A tracing algorithm of Thevenin equivalent parameters for power systems with large disturbance［J］.Proceedings of the CSEE，2012，32（22）：126-132.

［21］汤涌，易俊，侯俊贤，等.基于时域仿真的戴维南等值参数跟踪计算方法［J］.中国电机工程学报，2010，30（34）：63-68.TANG Yong，YI Jun，HOU Junxian，et al.Calculation method for Thevenin equivalent parameters based on time domain simulation［J］.Proceedings of the CSEE，2010，30（34）：63-68.

［22］仲悟之.受端系统暂态电压稳定机理研究［D］.北京：中国电力科学研究院，2008.ZHONG Wuzhi.Mechanism research of transient voltage stability in receiving-end grid［D］.Beijing：China Electric Power Research Institute，2008.

［23］罗建，徐馨，杨桦，等.微小扰动状况下的戴维南等值参数辨识方法［J］.中国电机工程学报，2014，34（增刊）：61-66.LUO Jian，XU Xin，YANG Hua，et al.Identification method for Thevenin equivalent parameters under tiny disturbance conditions［J］.Proceedings of the CSEE，2014，34（Supplement）：61-66.

［24］李卓艺，刘俊勇，刘友波，等.系统持续扰动下的电力系统戴维南等值参数在线识别［J］.中国电机工程学报，2015，35（8）：1900-1908.LI Zhuoyi，LIU Junyong，LIU Youbo，et al.An on-line parameter identification of Thevenin equivalent circuit for power systems with persistent disturbance［J］.Proceedings of the CSEE，2015，35（8）：1900-1908.

［25］贠志皓，丰颖，咸国富，等.计及发电机无功越限的广域戴维南等值参数在线计算方法［J］.电力系统自动化，2016，40（11）：53-60.YUN Zhihao，FENG Ying，XIAN Guofu，et al.Online computation method of wide area Thevenin equivalent parameters considering reactive power constraints of generators［J］.Automation of Electric Power Systems，2016，40（11）：53-60.

［26］秦文丽，林伟芳.在线电压分析方法及无功优化配置综述［J］.电气传动自动化，2013，35（1）：1-6.QIN Wenli，LIN Weifang.Overview of on-line voltage analysis methods and optimal reactive power configuration［J］.Electric Drive Automation，2013，35（1）：1-6.

［27］马世英，仲悟之，汤涌，等.基于多信息源的电压安全全过程预警及防控系统［J］.电网技术，2013，37（9）：2459-2465.MA Shiying，ZHONG Wuzhi，TANG Yong，et al.A multiple information sources based whole process early warning and preventive control system for voltage security ［J］.Power System Technology，2013，37（9）：2459-2465.

［28］夏道止.电力系统分析（下册）［M］.北京：水利电力出版社，1995：105-107.

［29］西安交通大学，清华大学，浙江大学，等.电力系统计算［M］.北京：水利电力出版社，1978：295-300，190-192.

［30］刘新文，王雪松.可逆分块矩阵的逆矩阵的求法［J］.衡阳师范学院学报，2008，29（3）：29-31.LIU Xinwen，WANG Xuesong.The method of inverse matrix of the inversable bolck matrix［J］.Journal of Hengyang Normal University，2008，29（3）：29-31.