利用智能水滴算法优化神经网络的MPPT

赵文清，李 瑶

（华北电力大学 控制与计算机工程学院，河北 保定 071003）

0 引言

光伏阵列是光伏发电系统的重要组成部分，其输出特性受多种外界因素影响，具有非线性特征。在光伏发电系统中使用最大功率点跟踪（MPPT）技术，能显著提高太阳能的转换效率［1-2］。

目前MPPT技术已成研究热点，国内外学者提出了多种控制算法，主要有恒定电压控制法、干扰观测法、电导增量法、模糊逻辑控制法等［3-4］。这些方法虽然结构简单，但是在实际应用中受环境影响，鲁棒性较差。神经网络具有逼近非线性映射的能力，可以很好地模拟光伏电池的非线性特征，具有很强的自适应性。文献［5］中采用针对光伏电池特性的PV神经网络对其建模，利用遗传算法对PV曲线进行寻优操作，取得了较高精度，提高了系统稳定性，克服了传统神经网络采集训练数据的难度。文献［6］提出遗传算法优化BP神经网络（BPNN）的建模方法，测试及仿真结果表明，该方法精度高，能够有效地反映光伏阵列的输入输出特性，体现了很好的自适应性。文献［7］将Elman神经网络（ElmanNN）应用于风功率预测，在环境变化时，仍能快速准确地预测风电输出功率。但由于ElmanNN采用误差反向传播算法（BP算法）修正权值，难免会存在陷入局部最优值、收敛速度慢等缺陷。

智能水滴 IWD（Intelligent Water Drop）算法是Shah Hosseini在2007年提出来的一种新兴群体智能算法［8］，是由模仿自然界水系统和其周围环境的相互作用而形成河道的过程进行迭代运算，最后得到优化的结果。该算法已成功运用在组合优化（旅行商［8］、多背包［9］）、生产调度［10］、路径规划（单机无人机路径规划［11］、机器人路径规划［12］）等多个方面。本文提出一种基于IWD算法优化ElmanNN权值向量和阈值向量的光伏系统MPPT模型。预测实例表明，利用IWD算法优化ElmanNN（IWD-ElmanNN）的方法与传统的ElmanNN方法相比，具有较高的预测精度。

1 MPPT控制原理

光伏电池的最大输出功率是随外界环境变化而改变的，虽然是非线性的，但在任何光照强度和环境温度条件下，电池组件都会存在一个最大功率点。即使光强和温度都稳定不变，输出功率也会因为外接负载的不同而不同［13］。为了提高光伏电池的转换效率需采用MPPT技术，MPPT控制原理如图1所示。

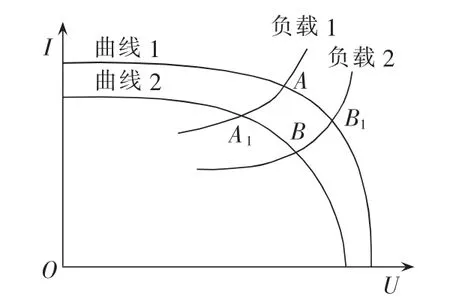
图1 MPPT控制原理Fig.1 Principle of MPPT control

图1中，曲线1、曲线2为光伏阵列在不同光照下的I-U特性；若某一时刻的光照使得电池输出为曲线1，此时对应的最大功率点为A处。当光照改变，电池输出曲线变为曲线2时，系统的工作点会偏移到A1处，为了使功率点最高，则需要调整负载，使得系统输出工作点运行在B处，即当外界环境变化时，实时调整负载大小使系统始终工作在最大功率点，以提高光伏阵列的输出功率。

2 ElmanNN

ElmanNN由Jeffrey L.Elman于1990年提出，是一种典型的局部反馈神经网络。该模型具有反馈环节，网络结构如图2所示，分为4层：输入层、隐含层、承接层和输出层。承接层（或状态层）是ElmanNN特有的层，该层从隐含层接受反馈信号，记忆隐含层前一时刻的输出值，输出经延迟与存储再输入隐含层。除承接层以外，其余3层结构的连接与前馈网络类似［14-15］。

图2 ElmanNN结构图Fig.2 Structure of ElmanNN

根据图 2，网络的输出 y（k）由式（1）确定。

其中，w3为隐含层到输出层的权值矩阵；b2为输出层阈值；g（x）为输出层传递函数。

隐含层输出x（k）表达式为：其中，w1、w2分别为输入层到隐含层、承接层到隐含层的权值矩阵；u（k-1）为输入向量；b1为隐含层阈值；f（·）为隐含层神经元的传递函数；xc（k）为承接层在第k步时到隐含层的反馈输出，如式（3）所示。

ElmanNN采用误差反向传播算法（BP算法）修正权值，误差函数定义为：

其中为实际输出；y（k）为期望输出。

3 利用IWD算法优化ElmanNN

IWD算法是一种新兴的群体智能优化算法，在解决复杂的优化问题中，它比其他群智能算法更具优势。基于上述特点，本文提出用IWD算法优化ElmanNN权值和阈值这一新思路。

3.1 IWD算法的数学描述

IWD算法是模拟自然界中水滴运动的过程而被发明的。可以构建一个抽象的数学模型，称为智能水滴，它具有2个重要性质：水滴携带的泥土量和水滴当前前进的速度。水滴在路径中流动时，它的2个性质都会发生改变，算法的目标是按照某些约束条件寻找到从起点到终点的一条最佳路径。

假设在节点i的速度为v（i），在节点j的速度为v（j），其值与节点 i到节点 j间路径中的泥土量 s（i，j）呈非线性反比关系，表达式如下：

其中，av、bv、cv为用户预先设定的静态参数。

当水滴k由节点i移动到节点j时，水滴携带泥土变化量 Δs（IWD）和路径中的泥土变化量 Δs（i，j）是相等的，泥土变化量 Δs（i，j）与水滴由节点 i流动到节点 j所需时间 t（i，j）呈非线性反比关系：

其中，as、bs、cs为用户预先设定的静态参数；t（i，j）为水滴由节点i流动到节点j所需时间，如式（8）所示。

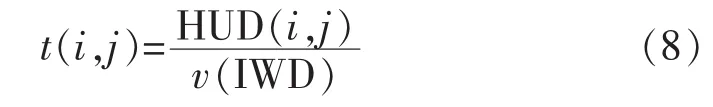
其中，HUD（i，j）为定义的反向启发函数，为水滴拒绝移动的程度，与节点i到节点j之间的距离成正比。

从节点 i到节点 j，水滴携带的泥土量s（IWD）和路径中泥土量 s（i，j）的更新公式为：

其中，ρnϵ（0，1），为权重系数，一般取值 0.9。

在水滴移动过程中，可能出现多条路径，河床中的泥土阻碍水滴前进，水滴倾向于找到一条最容易的路径流向目的地，即含泥土量最少的路径。假设水滴在节点i时选择j为下一节点的概率为其表达式如下：

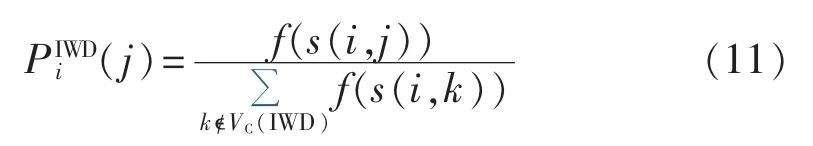
其中，s（i，j）为节点 i到节点 j路径上的泥土量；VC（IWD）为水滴流过的节点集；f（s（i，j））的表达式见式（12）。

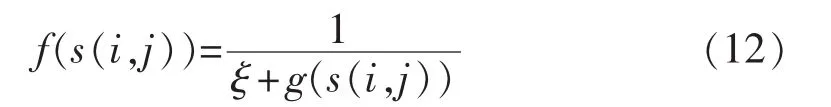
其中，ξ为极小的正数，其作用是保证函数f的分母不为零；函数g的功能是保证节点i、j之间的泥土量s（i，j）非负，表达式如式（13）所示。

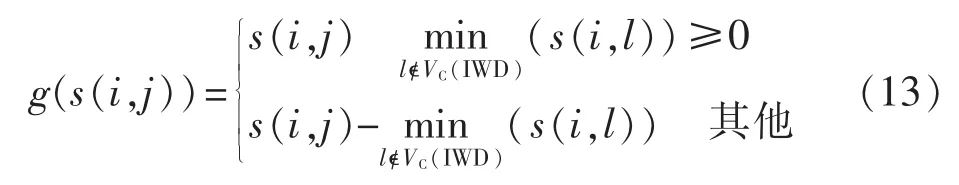
其中，函数min表示当前节点i到与所有能选择的下一节点 l之间泥土量 s（i，l）的最小值。

3.2 算法改进

由水滴路径选择概率公式可知，当出现以下情况时，算法容易陷入局部收敛：

a.当一条路径的选择概率远远大于其他路径时，水滴无法选择其他路径；

b.当多条路径含有的泥土量比较少，且差别不大时，水滴很难选择下一节点。

针对基本IWD算法易因节点的选择机制不当而出现陷入局部最优解的问题，本文加入参数φ对其进行改进。

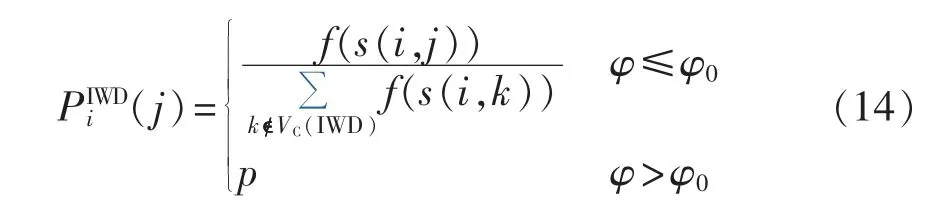
其中，φ，pϵ（0，1）为随机数；φ0为常数。

水滴在选择下一节点前先为φ随机赋值，作用是增加选择概率的随机性。通过φ与φ0的大小比较，确定选择节点j概率的计算公式。通过引入常数φ0，增加水滴选择其他路径的概率，使水滴路径选择多样化，更加有利于快速找到最优解。

每次迭代都会得到一个当前最优解TIB，最优解所包含的路径称为精英路径，得到最优解的IWD称为精英水滴。为了使前一次迭代得到的精英路径在下一次迭代中被水滴选择的概率更高，每次迭代后按式（15）对精英路径中的泥土量进行更新。

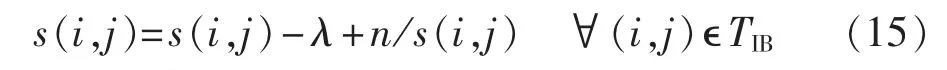
其中，λ为常数；n为精英水滴的个数。

3.3 IWD算法优化ElmanNN

建立ElmanNN后，利用IWD算法优化ElmanNN权值、阈值，它们的取值直接影响着神经网络的性能。基本思想为：首先确定每个参数的取值范围，假设网络中需要优化的参数为u1—um，共m个参数，对于任一参数ui，其可能的取值构成的集合为Iui，水滴从每个集合（Iu1—Ium）中遍历取值。选取均方误差MSE（Mean Square Error）作为评价指标，对每一个参数组合进行验证，重复这一过程，直到达到最大迭代次数或满足误差要求。选择MSE最小值所对应的参数作为ElmanNN最优参数。具体寻优过程描述如下。

4 基于IWD-ElmanNN的光伏系统MPPT

4.1 光伏系统MPPT

基于IWD-ElmanNN的光伏系统MPPT控制系统如图3所示，利用IWD算法对ElmanNN的权值和阈值进行优化，然后用优化后的ElmanNN预测最大功率点的工作电压Um，并将预测的最大工作点电压Um设定为恒电压控制法的参考电压Umref。DC／DC包含1个双向全桥电路，可以用来调节输出电压。当光伏发电系统的工作环境发生变化时，实时根据预测得到的Um来修改Umref，从而达到MPPT的目的，使光伏系统始终工作在最大功率处。

图3 基于IWD-ElmanNN预测的MPPT控制系统Fig.3 MPPT control system based on IWD-ElmanNN

4.2 预测过程

基于IWD-ElmanNN的光伏系统MPPT的预测过程描述如下。

a.数据预处理。利用式（16）对样本数据进行归一化。

其中，X为原始数据值；为归一化后的数据；Xmin、Xmax分别为原始数据X中的最小值、最大值。

b.采集光伏电站的光照和温度数据，划分出训练样本和测试样本。

c.根据所采集的样本数据，构造ElmanNN。

d.利用IWD算法优化ElmanNN的权值和阈值，具体算法参照3.3节。

e.使用训练好的IWD-ElmanNN对测试样本进行预测，并对预测结果进行误差分析。

5 实例预测及结果分析

5.1 研究对象

本文以中国某光伏电站示范验证平台于2015年8月1日至7日在06：00—18：00的实测数据为实验样本，样本数据每1 min采样一次，为满足预测需求，将每15 min内的数据做平均值处理，即每天48个样本点。样本数据为电站在不同时刻的环境温度T、光照强度L和最大功率点处的电压，部分实验数据样本如表1所示。

表1 部分实验样本Table 1 Partial experimental samples

将电站8月1日至6日的数据作为训练样本，将8月7日的数据作为测试样本。为验证IWD算法优化ElmanNN的预测效果，利用MATLAB进行编程，分别使用 BPNN、ElmanNN和IWD-ElmanNN 3种预测方法对表1的测试样本进行预测，预测值与实际值的曲线如图4所示。

图4 电压预测误差曲线Fig.4 Error curves of voltage prediction

5.2 参数设定

在表1中输入向量维数为2，即输入神经元数目为2，由影响光伏系统最大功率输入的主要因素组成。目标输出向量维数为1，即输出神经元数目为1，隐含层神经元数目设为5。网络的最大训练次数设为500，训练的目标误差设为0.001。根据文献［6-10］的实验测试和结果，对IWD算法中的参数进行设置，其中水滴的初始速度为1，水滴初始携带的泥土量为0，IWD 数为 40，扰动参数为 0.8，ρn=0.9，av=as=1，bv=bs=0.01，cv=cs=1。

5.3 结果分析

本文从预测结果的训练效率和预测误差两方面进行分析，验证IWD-ElmanNN的有效性。

a.训练效率。

同时对BPNN、ElmanNN和IWD-ElmanNN 3种预测方法进行训练，为了方便比较，3种方法采用完全一样的输入输出和训练数据。

图5 IWD-ElmanNN的训练误差曲线Fig.5 Curve of training error vs.training times of IWD-ElmanNN

由于篇幅限制，本文只给出了IWD-ElmanNN和ElmanNN训练误差曲线，分别见图5、图6。由图5可知，IWD-ElmanNN的训练最终误差为0.0097654，训练次数为85；由图6可知，ElmanNN的训练最终误差为0.009 979 8，训练次数为 121；训练结果显示IWD-ElmanNN的训练最终误差和训练次数均优于传统ElmanNN。

图6 传统ElmanNN的训练误差曲线Fig.6 Curve of training error vs.training times of traditional ElmanNN

b.预测误差。

为了评估预测结果的准确性，误差评价函数采用平均绝对百分比误差MAPE（Mean Absolute Percentage Error）和均方根误差 RMSE（Root of the Mean Squared Error）。

表 2为 BPNN、ElmanNN 和 IWD-ElmanNN 3种预测方法预测结果的比较。由表2可知，IWDElmanNN的RMSE为2.2062 V，在3种方法中最低；同时MAPE为8.1378%，在3种方法中也最低，同Elman-NN和BPNN相比，分别降低了2.812 2%和5.1911%；由实验结果可知IWD-ElmanNN的MAPE和RMSE均优于ElmanNN和BPNN。BPNN预测精度较低，这是因为初始权值和阈值的选取对网络造成的影响较大，ElmanNN具有反馈环节，收敛速度较快。

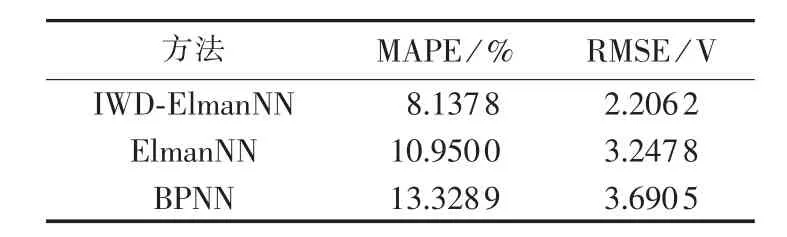
表2 3种预测方法的MAPE和RMSETable 2 MAPE and RMSE of three prediction methods

6 结论

本文给出一种基于IWD-ElmanNN的光伏系统MPPT预测方法，使用IWD算法对ElmanNN的权值和阈值进行优化。预测实例表明，与传统的ElmanNN相比，本文提出的IWD-ElmanNN方法具有更高的预测精度、更快的收敛速度，为MPPT控制算法的改进提供了一种新思路，克服了传统MPPT控制算法控制精度低、容易发生误跟踪的缺点，实现光伏阵列最大工作点的准确预测，大幅提高了MPPT控制系统的性能。

参考文献：

［1］韩伟，王宏华，陈凌.光伏组件参数拟合及输出特性研究［J］.电力自动化设备，2015，35（9）：100-107.HAN Wei，WANG Honghua，CHEN Ling.Study on parameters fitting and output characteristics of photovoltaic module［J］.Electric Power Automation Equipment，2015，35（9）：100-107.

［2］李善寿，张兴.改进的光伏组件工程数学模型建模方法［J］.电力自动化设备，2015，35（9）：108-112.LIShanshou，ZHANG Xing.Improved mathematicalmodeling method for PV modules［J］.Electric Power Automation Equipment，2015，35（9）：108-112.

［3］陈剑，赵争鸣.光伏系统最大功率点跟踪技术的比较［J］.清华大学学报（自然科学版），2010，50（5）：700-704.CHEN Jian，ZHAO Zhengming.Comparison of maximum power point tracking techniques for photovoltaic systems［J］.Journal of Tsinghua University（Natural Science Edition），2010，50（5）：700-704.

［4］孙博，梅军，郑建勇.局部阴影条件下最大功率点跟踪改进算法［J］. 电力自动化设备，2014，34（1）：115-119，127.SUN Bo，MEIJun，ZHENG Jianyong.Improved algorithm for maximum power point tracking under local shading condition ［J］.Electric Power Automation Equipment，2014，34（1）：115-119，127.

［5］龙洁.基于NN模型估计的光伏最大功率点跟踪控制技术研究［J］. 电力系统保护与控制，2011，39（20）：38-42.LONG Jie.Research on photovoltaicmaximum powerpoint tracking control based on NN model［J］.Power System Protection and Control，2011，39（20）：38-42.

［6］林虹江，周步祥，冉伊，等.基于遗传优化BP神经网络算法的光伏系统最大功率点跟踪研究［J］. 电测与仪表，2015，52（5）：35-40.LIN Hongjiang，ZHOU Buxiang，RAN Yi，etal.Research on maximum power point tracking of photovoltaic system based on genetic algorithm BP neural network algorithm［J］.Electrical Measurement and Instrumentation，2015，52（5）：35-40.

［7］杨楠，周峥，李臻.基于总体平均经验模态分解与改进Elman神经网络的风功率组合预测［J］. 电网与清洁能源，2015，31（10）：112-117.YANG Nan，ZHOU Zheng，LI Zhen.Wind power combination forecasting based on ensemble average empirical mode decomposition and improved Elman neural network［J］.Power Grid and Clean Energy，2015，31（10）：112-117.

［8］SHAH-HOSSEINI H.Problem solving by intelligent water drops［C］∥IEEE Congress on Evolutionary Computation，2007.CEC 2007. ［S.l.］：IEEE，2007：3226-3231.

［9］SHAH-HOSSEINI H.Intelligent water drops algorithm：a new optimization method for solving the multiple knapsack problem ［J］.International Journal of Intelligent Computing and Cybernetics，2008，1（2）：193-212.

［10］周季华，叶春明，盛晓华.基于智能水滴算法置换流水线调度问题的研究［J］. 计算机科学，2013，40（9）：250-253.ZHOU Jihua，YE Chunming，SHENG Xiaohua.The study of permutation flow shop scheduling problem based on intelligent water drop algorithm［J］.Computer Science，2013，40（9）：250-253.

［11］DUAN H，LIU S，WU J.Novel intelligent water drops optimization approach to single UCAV smooth trajectory planning［J］.Aerospace Science and Techology，2009，13（8）：442-449.

［12］SALMANPOUR S，OMRANPOUR H，MOTAMENI H.An intelligentwaterdropsalgorithm forsolving robotpath planning problem［C］∥IEEE 14th International Symposium on Computational Intelligence and Informatics（CINTI）.Budapest，Hungary：IEEE，2013：333-338.

［13］王红艳，万盟.基于粒子群算法的MPPT控制策略研究［J］.南京工程学院学报（自然科学版），2014，12（2）：24-27.WANG Hongyan，WAN Meng.Research on MPPT control strategy based on particle swarm optimization algorithm［J］.Journal of Nanjing Institute of Technology（Natural Science Edition），2014，12（2）：24-27.

［14］王晓霞，马良玉，王兵树.进化Elman神经网络在实时数据预测中的应用［J］. 电力自动化设备，2011，31（12）：77-81.WANG Xiaoxia，MA Liangyu，WANG Bingshu.Application of evolutionary Elman neural network in real time data prediction［J］.Electric Power Automation Equipment，2011，31（12）：77-81.

［15］尹东阳，盛义发，蒋明洁.基于粗糙集理论-主成分分析的Elman神经网络短期风速预测［J］. 电力系统保护与控制，2014，42（11）：46-51，90.YI Dongyang，SHENG Yifa，JIANG Mingjie.Elman neural network based on rough set theory and principal component analysis for short-term wind speed forecasting［J］.Power System Protection and Control，2014，42（11）：46-51，90.