基于故障辅助因子的配电网高容错性故障区段定位方法

郭壮志 ，陈 涛 ，洪俊杰 ，毛晓明 ，陈璟华

（1.河南工程学院 电气信息工程学院，河南 郑州 451191；2.广东工业大学 自动化学院，广东 广州 510006）

0 引言

配电网故障区段定位对于提高配电网自愈性和运行可靠性具有重要作用。随着配电网自动化终端设备的广泛应用，基于设备过电流信息的故障区段间接定位方法因原理简单、实现便捷而成为该领域的研究热点，该类算法主要分为2类：统一矩阵算法［1-5］和人工智能算法［6-13］。其中，统一矩阵算法直接利用线路元件两端状态监控信息构建故障辨识矩阵，具有建模直接、定位高效等优势，但对于运行信息畸变下的故障定位问题，容易出现错判或漏判。虽然一些学者已提出具有容错性能的统一矩阵算法，但通用性不强［4-5］。基于人工智能算法的配电网故障区段定位方法因具有高的容错性能且原理简单，近年来被大量研究，取得了丰硕的成果，众多新型的群体智能算法如遗传算法GA（Genetic Algorithm）、蚁群算法、仿电磁学算法、免疫算法、蝙蝠算法、和声算法等被应用于该领域。

基于群体智能算法的配电网故障区段定位方法的基本思想是：基于逼近理论和最小故障诊断集概念，构建故障定位离散优化数学模型，利用群体智能算法找出最能解释所有自动化设备上传故障电流报警信息的馈线短路故障区段。理论研究表明：该类方法只需对设备进行0-1编码，利用优化目标来描述故障设备的过电流信息逼近关系，具有建模原理简单、程序实现容易的优点，采用逼近思想使得所建故障定位模型不仅具有强通用性，且进行故障区段辨识时具有高容错性，并可直接采用新型高效的群体智能算法进行优化决策。

文献［6-8］提出基于遗传算法的配电网故障定位逼近建模理论与决策算法。但文献［6］因模型对馈线故障和自动化设备过流信息间的逼近关系描述不准确，会造成无畸变状态信息下的故障区段误判。文献［7］首次建立基于遗传算法的高级故障区段定位间接模型，不仅有效解决了文献［6］的模型误判问题，且具有很高的容错性，但对多区域故障定位存在重复性定位问题。文献［8］在文献［7］的基础上提出了多区域故障定位的分支选择法。文献［9］建立分级的故障区段定位逼近模型并采用蚁群算法对其进行优化求解。文献［10］基于文献［8］建立更为简单的多区域配电网故障时的区段定位统一数学模型，并应用仿电磁学算法提高故障定位效率。文献［11-12］仍然沿用文献［6-10］的间接故障定位模型逻辑建模思想，将免疫算法、蝙蝠算法应用于故障区段定位模型的寻优决策。文献［13］基于功率流参考正方向，构建含分布式电源配电网的故障定位间接模型，并采用和声算法进行模型决策求解。

但上述方法存在固有缺陷：所建的0-1离散故障定位模型是基于逻辑值关系构建，不能够采用高效的梯度算法或松弛方法进行决策求解；采用群体智能算法进行优化时理论上具有全局收敛性，但在实际决策时因优化搜索存在随机性，将会因算法早熟而产生数值稳定性问题，从而造成故障定位结果具有一定的不确定性；因为目前采用群体智能优化算法进行求解，应用于大规模配电网故障定位时决策效率低。

对基于群体智能算法的间接故障定位方法进行综合分析易得出：基于逻辑关系描述进行故障定位模型构建是导致配电网区段间接定位模型存在上述缺陷的根本原因。因此，建立非逻辑关系描述为基础的故障区段辨识模型成为有效克服当前间接故障定位模型和算法不足之处的关键。

本文基于代数关系描述，以单一故障假设为前提，首先建立无畸变故障电流信息情况下配电网故障区段定位的线性方程组模型；在此基础上，利用互补约束条件、光滑互补函数和最优化极值理论，构建了电流信息畸变情况下故障辅助因子数学模型，进而建立具有高容错性特征的非线性方程组描述的配电网故障定位新模型，并采用牛顿-拉夫逊法进行求解，具有二阶收敛特性，且能够有效实现多重馈线短路故障区段的辨识。

1 无信息畸变时故障定位线性方程组模型

1.1 故障报警信息与设备状态编码方法

配电网正常运行时，配电系统无电流越限情况；配电网发生故障时，监控节点处馈线终端设备（FTU）等自动化设备将会检测到短路故障过电流，并通过远程通信设备将带时标的故障报警信息上传到控制主站。可以看出，不需要知道过电流的具体量值，只要依据FTU等是否监测到过电流即可判定配电网是否发生短路故障。因此，可以采用故障和正常这2种状态来描述故障报警信息情况，本文采用0表示无故障报警信息，采用1表示控制主站收到时标报警信息。

本文仍然采用文献［6-13］的间接建模方法，其本质上是利用假定馈线故障时所造成的电流越限信息逼近时标过电流报警信息。因此，可利用正常和故障2种状态来表示馈线所在区段是否发生故障，本文以馈线支路的故障状态信息作为内生变量，并采用0-1离散值进行变量编码，数字0表示馈线区段运行正常，数字1表示馈线区段发生故障。

1.2 基于代数关系描述的开关函数模型

配电网故障定位间接方法的最终目的是找出相应发生故障的设备，其最能解释所有上传的故障电流报警信息。因此，建立数学模型合理有效地描述馈线运行状态与时标过电流报警信息间的耦合关联关系则成为定位故障馈线的关键。文献［6-13］给出了开关函数的概念与构建方法。开关函数实质上就是描述馈线故障与短路过电流信息间的耦合关联关系，是构建间接故障定位模型的基础。文献［6-13］构建了基于逻辑描述的开关数学模型，其构建方法导致决策算法过分依赖群体智能算法，因而存在数值稳定性问题和应用于大规模配电网故障定位时效率不高的缺点。

本文提出基于代数关系描述的开关函数模型，其构建方法为：首先采用因果关联分析理论找出与监控点上传故障报警信息直接相关的所有可能故障设备，即因果关联设备；基于单一馈线故障假设和故障诊断最小集理论建立开关函数代数关系模型。下面以图1所示简单辐射状配电网为例，详细阐述开关函数代数关系描述数学模型的构建方法。

图1 简单辐射状配电网示意图Fig.1 Schematic diagram of simple radial distribution network

当断路器S1的监控点捕获到故障过电流信息时，将通过通信设备向控制主站上传报警信息，依据图论的图连通性和电力功率流的传输特性可知，可能是馈线1—5发生短路故障，从而引起S1处的过电流，其为造成断路器S1报警信息的因果关联设备。同理，可得到馈线2—5为分段开关S2报警信息的因果关联设备，馈线3—5为分段开关S3报警信息的因果关联设备，馈线4、5为分段开关S4报警信息的因果关联设备，馈线5为分段开关S5报警信息的因果关联设备。表1为图1中各自动化开关的因果关联设备情况，其中A B表示馈线B紧邻馈线A且功率流由A流向B。

表1 因果关联设备信息Table 1 Information of related causal devices

依据各自动化开关的因果关联设备与顺序构建开关函数，且其必须直接反映因果关联设备与相应自动化开关报警信息间的因果关联性。依据因果关联设备的确定方法可以知道，因果关联设备之间具有并联叠加特性，即因果关联设备单独发生短路故障或同时发生故障，都会导致自动化开关的故障过电流。在代数运算中，“+”运算蕴含着并联叠加特性，因此，本文中利用代数“+”运算代替文献［6-13］中的逻辑或运算来构建开关函数。如果IS1（X）—IS5（X）分别表示自动化开关S1—S5的电流越限信息的开关函数，x（1）—x（5）分别表示馈线 1—5 的馈线运行状态信息，则 IS1（X）—IS5（X）的代数描述数学模型可以表示为：

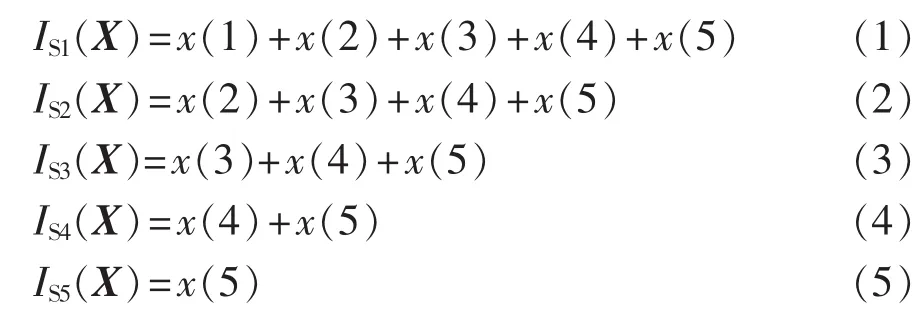
式（1）—（5）中代数“+”运算蕴含着所有因果关联设备与监控点上传报警信息的因果联系，揭示了馈线故障状态的协同作用对报警信息的直接作用特性。

依据上述开关模型的构建方法，当具有N个自动化监控终端时，基于代数关系描述的开关函数数学模型可表示为：

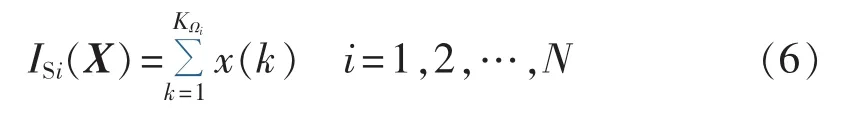
其中，Ωi为自动化开关Si的因果关联设备集；KΩi为Ωi中因果关联设备数。

1.3 配电网故障区段定位的线性方程组模型

在数值分析中，采用样本点残差平方和衡量样本值和理想值之间的一致逼近程度，其优点在于可对称考虑正负偏差。因此，本文采用残差平方和来衡量开关函数和上传报警信息间的逼近程度。令I*Si为自动化开关Si上传的报警信息，其逼近数学模型可以表示为：

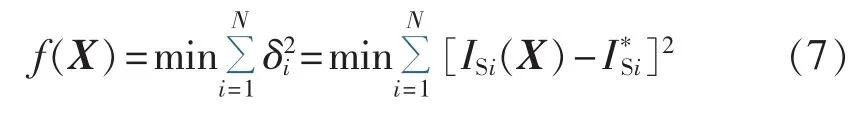
在无报警信息畸变情况下，当找到最佳故障设备时，应使所有上传报警信息与开关函数间总偏差为0，即f（X）值为0，否则将会导致馈线故障区段的错误辨识。由式（7）可知，只有当所有δi的值为0时，f（X）的值才为0。在无信息畸变情况下，准确定位出故障馈线时，以下等式关系必然满足：

反之，根据式（8）可用来辨识无信息畸变时的馈线故障区段。无信息畸变时的故障区段定位的线性方程组模型可表示为：

其中，AϵRN×N，其元素 aij=0 或 1。

1.4 故障定位线性方程组模型的适应能力分析

式（9）所建故障定位线性方程组新模型，能正确辨识馈线故障区段需满足以下条件：方程组的解必须存在且具有唯一性；方程组解集中自变量值只能为0或1；数值1所对应的故障馈线应和预设故障具有一一对应关系。下面以图1所示的配电网为例分析新故障定位模型的适应性。

在无信息畸变情况下，假定馈线5发生故障，则故障定位线性方程组中：

利用线性代数行初等变换可得到矩阵A的秩R（A）和增广矩阵相等，且等于变量个数。根据线性方程组解的唯一性存在定理可知［14］：馈线5发生故障时，配电网故障区段定位线性方程组模型具有唯一解。系数矩阵A是上三角矩阵，利用数值计算方法中线性方程组求解的前推回代算法易于得到故障定位线性方程组的解为：

由式（12）可知，方程组的解满足自变量的值只能为0或1这一条件。且依据1.2节的编码方法可辨识出馈线5发生短路，与预设故障一致。同理，可验证预设故障发生在馈线1—4时所提故障定位模型能够准确定位出馈线故障区段。因此，在无信息畸变情况下，所建故障定位线性方程组模型对于短路故障辨识具有强的适应性，能够精确地定位出故障所发生的区段。

配电网自动化设备的运行环境比较恶劣，监控终端容易出现故障报警信息上传缺失或畸变情况。预设馈线 5 发生短路故障，若即 S2的电流越限信息出现畸变，此时系数矩阵A仍然为式（11）。按照无信息畸变时的分析方法，此时配电网故障区段定位线性方程组模型具有唯一解，其方程组的解为：

从式（13）可看出，依据编码方法将会判定馈线1和5发生故障，出现了误判情况。同理，可分析其他畸变情况下也难于准确定位出短路故障馈线。因此，可看出所建故障定位线性方程组模型缺乏对信息畸变时的适应性，必须在此基础上构建具有容错性能的故障定位模型。

2 基于辅助因子的故障定位容错性方程组模型

根据式（13）可以看出，信息畸变时已不能保证方程组解的取值为0或1，从而导致误判。本节将基于逼近关系理论和代数关系描述，建立具有容错性能的故障定位非线性方程组模型，建模的基本思路为：首先，对自变量的取值进行约束，即融入0-1离散约束条件；其次，利用文献［6-13］的配电网故障定位最优化方法的逼近关系理论，采用0-1离散约束条件的互斥性条件，建立基于代数关系描述的偏差平方和最小的互补约束优化模型；再次，利用光滑优化辅助函数构建等价的残差平方和最小的连续空间非线性规划模型，以避免对离散变量的直接决策求解；最后，为进一步提高故障定位效率，基于最优化模型极值的KKT条件构建容错故障定位模型的容错因子，建立高容错性配电网故障辨识的非线性方程组模型。其详细步骤如下。

依据第1节理论分析和馈线状态约束限制，构建的残差平方和最小优化模型为：

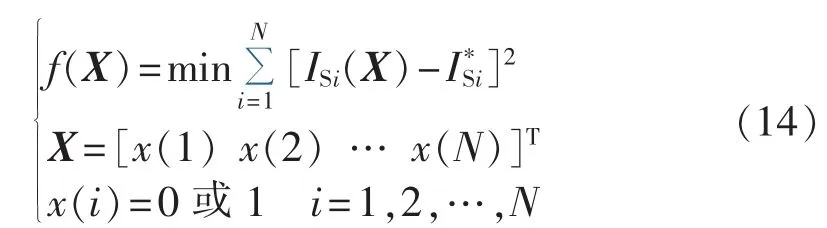
实际上，馈线的故障信息状态具有互斥性，即同一馈线故障状态x（i）取值不能同时为0或1，因此，可构建辅助互补约束条件将式（14）等价影射为连续空间的残差平方和最小优化模型，其馈线状态离散约束的互补模型为：

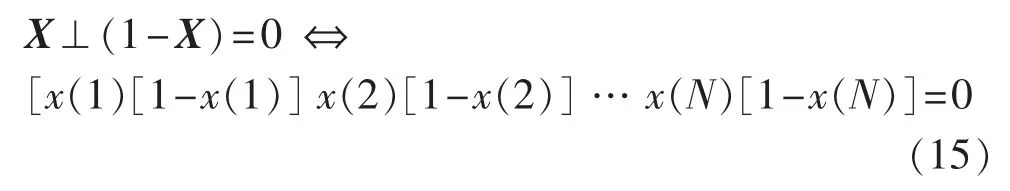
其中，⊥表示垂直互补。

由式（15）可看出，在优化过程中无需要求自变量的离散性，在获得最优解时都可保证最终的决策变量值为0或1。连续空间的残差平方和最小的互补约束优化模型可表示为：

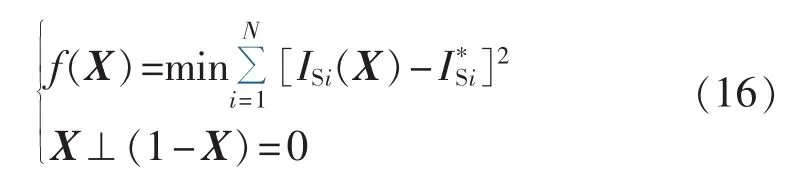
简单线性互补约束优化也是一个非确定性多项式（NP）难问题［15］，互补光滑函数可等价代替互补约束条件，使其可等价转化为一般非线性规划问题，不仅可使可行点满足非线性约束规格，且便于利用原优化问题获得最优值时的等效KKT必要条件。本文将利用互补光滑函数优化模型的KKT条件构建故障辅助因子。

常用的互补函数为Fischer-Burmeister函数，即其具有扰动因子的互补光滑函数的数学模型通常为：

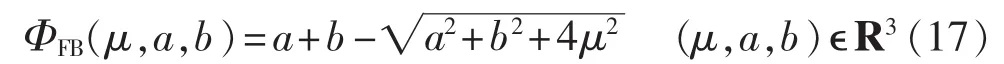
根据文献［16］定理，当 μ 0时，式（17）等价为：

利用 ΦFB（μ，a，b）=0 作为式（16）的替代约束条件［16］，从而将互补约束定位模型光滑化，式（16）转化为：

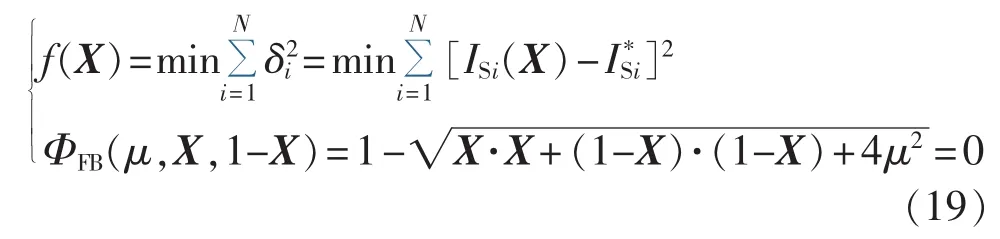
依据文献［17］给出的光滑优化模型收敛定理可得出结论：当μ 0时，互补约束光滑模型最优解渐近收敛于二阶必要条件的渐近稳定点。因此，可构造拉格朗日函数确定KKT条件，将优化问题式（19）等价地转化为带有非负参数μ的光滑方程组，其数学模型为：

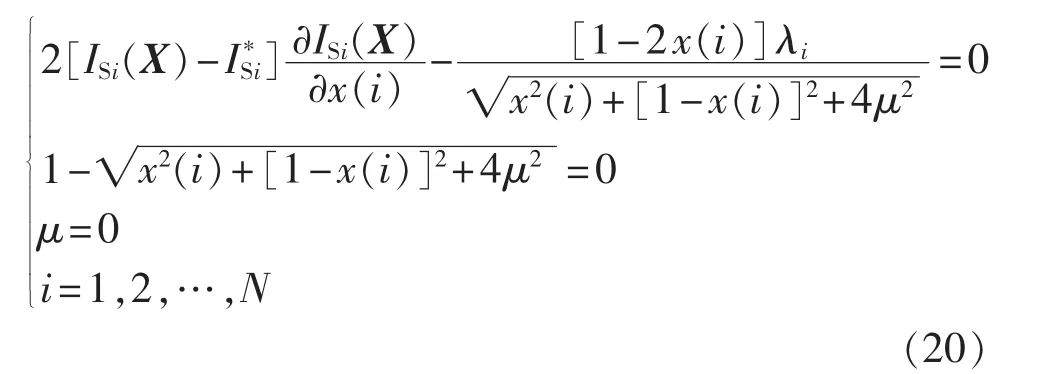
令：

依据文献［18］的光滑重构方法，通过加入正则因子μ来改善算法全局收敛性和数值计算效果，可得到式（20）的光滑重构方程组H（Z）为：

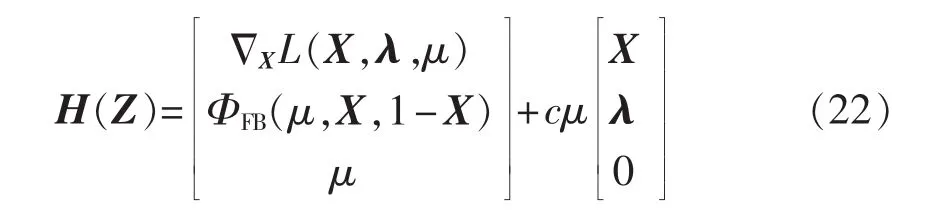
其中，c为加速因子；λ为拉格朗日乘子列向量。

根据式（14）中目标函数的二次形式及无信息畸变下故障定位线性方程组数学模型式（9），可将式（22）写成以下标准型：

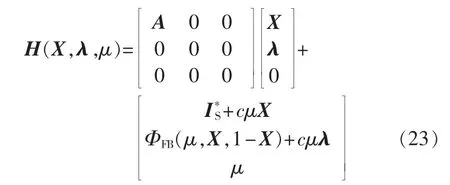
式（23）的值等于0，即为信息畸变下配电网故障定位的非线性方程组模型，即：

与式（9）相比，式（24）增加了 3 个部分，其中 μ与 ΦFB（μ，X，1-X）+cμλ 是为了保证式（15）在找到方程组解集时离散约束条件成立，而cμX是为了提高报警信息畸变情况下故障定位模型的容错性能，本文定义为故障辅助因子。

3 配电网故障定位非线性方程组的求解

式（24）是最高次为2次的非线性方程组，本文采用牛顿-拉夫逊法进行求解，具体算法迭代求解数学模型的推导原理可参阅数值计算方法教材［19］。牛顿-拉夫逊法用于故障定位模型迭代求解的数学模型可表示为：

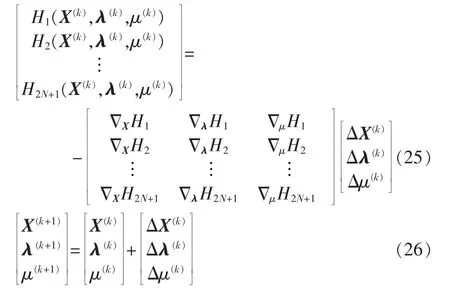
故障定位的基本步骤如下：

a.选取 cϵ（0.5，2），（X（0）， λ（0），μ（0））＝E（E 为单位矩阵）；

b.判断‖H（X（k）， λ（k）， μ（k））‖2的值，若其值为0则算法终止，否则转步骤c；

c.利用式（25）计算［ΔX（k）Δλ（k）Δμ（k）］T；

d.利用式（26）计算［X（k+1）λ（k+1）μ（k+1）］T，并计算‖H（X（k），λ（k），μ（k））‖2的值，转步骤 b。

因故障定位模型H（X，λ，μ）＝0的自变量最高次数为 2，（X*，λ*，μ*）为其不动点，依据牛顿-拉夫逊法的迭代公式和收敛阶的定义，可证明此时算法具有二阶收敛特性。详细证明过程可参阅文献［19］。

4 算例仿真分析

4.1 简单辐射状配电网算例

图1所示简单的5节点辐射状配电网，包含1台断路器、4个联络开关，5条馈线对应5个定位区段，以其为例进行仿真。根据第1节理论分析可知，在无信息畸变时线性方程组模型可准确辨识出馈线短路区段。因此，只验证在无信息畸变和有信息畸变情况下基于辅助因子的配电网故障定位非线性方程组模型的有效性。

在无信息畸变的情况下，分别对馈线1—5发生单一短路故障的情况进行仿真。自变量初值全部取值为1，加速因子c的初始化值为1.5，算法终止条件为‖H（X（k），λ（k），μ（k））‖2的值小于 10-6或最大迭代次数为100，2个条件满足其一则算法终止。表2为无信息畸变时的故障定位仿真结果。

根据表2可以看出，在无报警信息畸变情况下，基于辅助因子的配电网故障定位非线性方程组模型可准确地辨识出馈线故障区段。此时，拉格朗日乘子向量λ为零向量，正则因子μ的值为0，与式（9）对比可知，非线性方程组模型等价于无信息畸变下的故障定位线性方程组模型。因此，其可准确地定位出馈线的故障区段。观察定位出故障区段时算法的KKT值，易于看出其满足式（19）所示目标函数获得极值时的KKT条件。另外，在5种预设故障下，找到故障区段时算法的迭代次数不超过12次，表明算法搜索效率高。

在有电流报警越限信息畸变情况下，分别针对具有1～3位信息畸变的情况进行仿真，参数初始化值和算法终止条件与无信息畸变情况时相同。表3为信息畸变情况时的故障定位仿真结果。

根据表3可以看出，在有1～3位电流越限报警信息畸变情况下，基于辅助因子的配电网故障定位非线性方程组模型同样可准确地辨识出馈线故障区段。此时，正则因子μ的值为0，但拉格朗日乘子向量λ不再为零向量。观察向量λ易知，在简单辐射状配电网中，其非零元素刚好对应畸变位，其物理意义在于为保证信息畸变情况下自变量离散取值时的等式成立而通过辅助因子进行动态调整，同时可对报警信息畸变位置进行准确辨识，为监测装置的维护和检查提供了依据。

观察定位出故障区段时算法KKT值，易于看出其满足式（19）所示目标函数获得极值时的KKT条件。另外，在4种预设故障下，找到故障区段时算法的迭代次数不超过13次，表明算法搜索效率高。同时与无信息畸变情况下的算法迭代次数相比，有信息畸变情况下算法的迭代次数基本保持不变，表明算法具有很好的稳定性。

4.2 具有T型耦合节点配电网算例

为了进一步验证基于辅助因子配电网故障定位非线性方程组模型的合理性与有效性，对具有T型耦合节点的配电网进行仿真。图2为7节点T型耦合节点配电网，具有1台断路器、6个联络开关，7条馈线对应7个定位区段，以其为例进行分析。同样只验证在无信息畸变和有信息畸变情况下基于辅助因子的故障定位非线性方程组模型的有效性。

表2 无信息畸变时的故障定位仿真结果Table 2 Simulative results of fault locating without information distortion

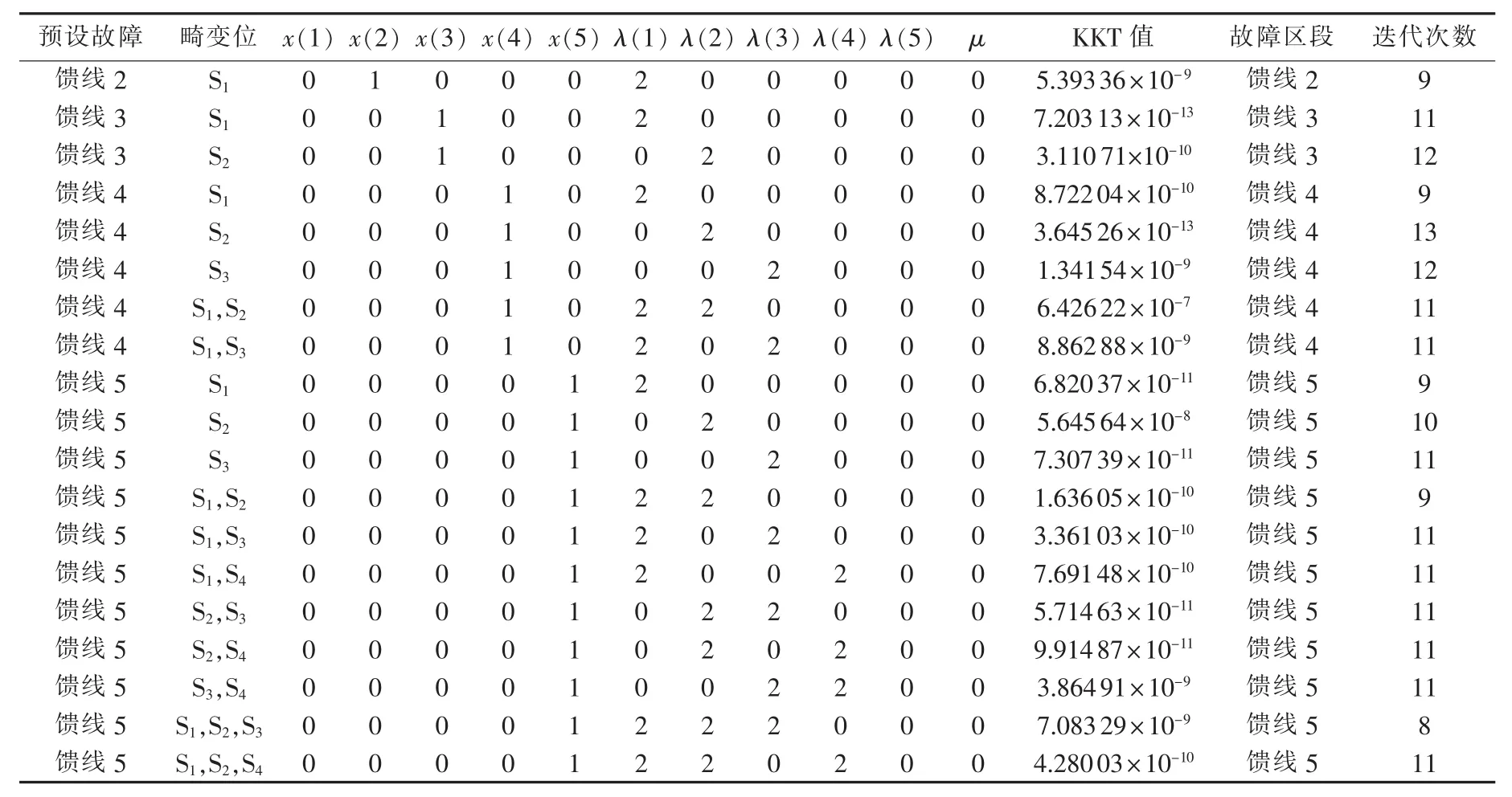
表3 信息畸变下的故障定位仿真结果Table 3 Simulative results of fault locating with information distortion

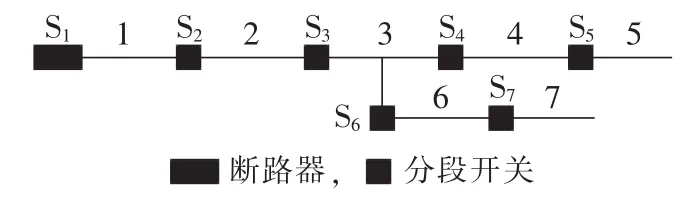
图2 单电源T型耦和节点配电网示意图Fig.2 Schematic diagram of single-source distribution network with T-type coupling node

在无信息畸变情况下，分别对馈线1—7单一短路故障和双重故障的情况进行仿真，参数初始化值和算法终止条件与4.1节相同。

表4为无信息畸变时的故障定位结果。可以看出，在无报警信息畸变情况下，针对含T型耦合节点的配电网，基于辅助因子的故障定位非线性方程组模型可准确地辨识出馈线故障区段，且可以实现双重故障的准确定位。此时，正则因子μ的值为0。在单一故障下，非线性方程组模型等价于无信息畸变下的故障定位线性方程组模型式（9）。但式（9）在多重故障下将会误判故障馈线位置，而非线性方程组模型因加入辅助因子，能实现对多重故障的准确辨识，这是与式（9）相比在无信息畸变情况下的显著优点。观察定位出故障区段时算法的KKT值，易看出其满足式（19）所示目标函数获得极值时的KKT条件。另外，在9种预设故障下，找到故障区段时算法的迭代次数不超过10次，表明算法搜索效率高。

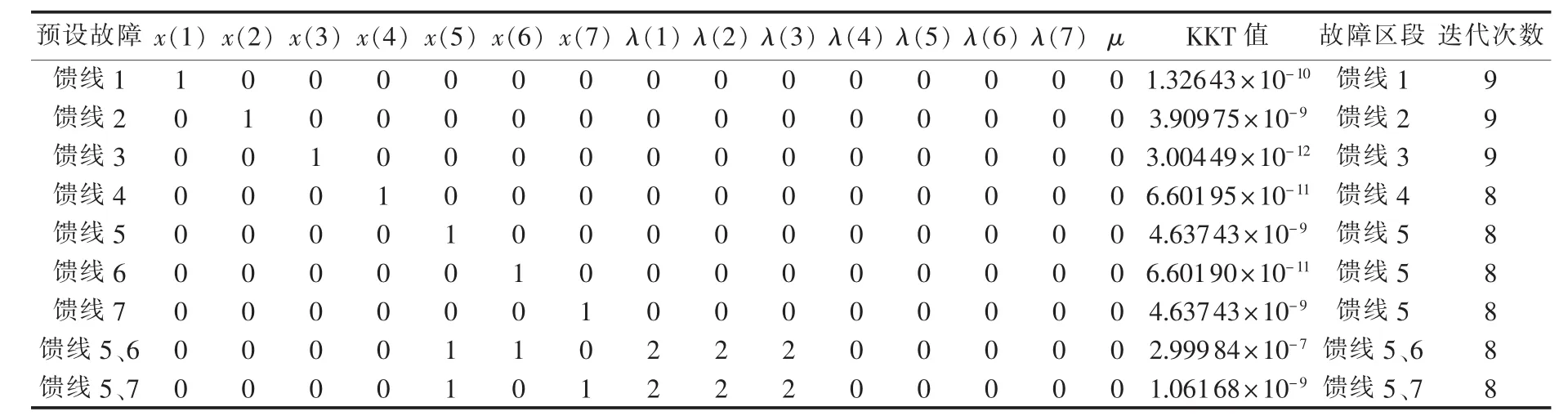
表4 无信息畸变时的故障定位仿真结果Table 4 Simulative results of fault locating without information distortion

表5为有电流越限报警信息下部分典型故障情况的仿真结果。根据表5可以看出，在有1～3位电流越限报警信息畸变情况下，基于辅助因子的配电网故障定位非线性方程组模型同样可准确地辨识出含T型耦合节点配电网的单一和多重馈线故障区段。此时，正则因子μ的值为0，但拉格朗日乘子向量λ不再为零向量。观察向量λ易知，单一故障下其非零元素刚好对应畸变位，但在双重故障下，λ的非零元素已无上述含义，其物理意义在于为保证信息畸变情况下自变量离散取值时等式成立而通过辅助因子进行动态调整。

观察定位出故障区段时算法KKT值，易看出其满足式（19）所示目标函数获得极值时的KKT条件。另外，在5种预设故障下，找到故障区段时算法的迭代次数不超过11次，表明算法搜索效率高。同时与无信息畸变情况下的算法迭代次数相比，有信息畸变情况下算法的迭代次数基本保持不变，表明算法具有很好的数值稳定性。

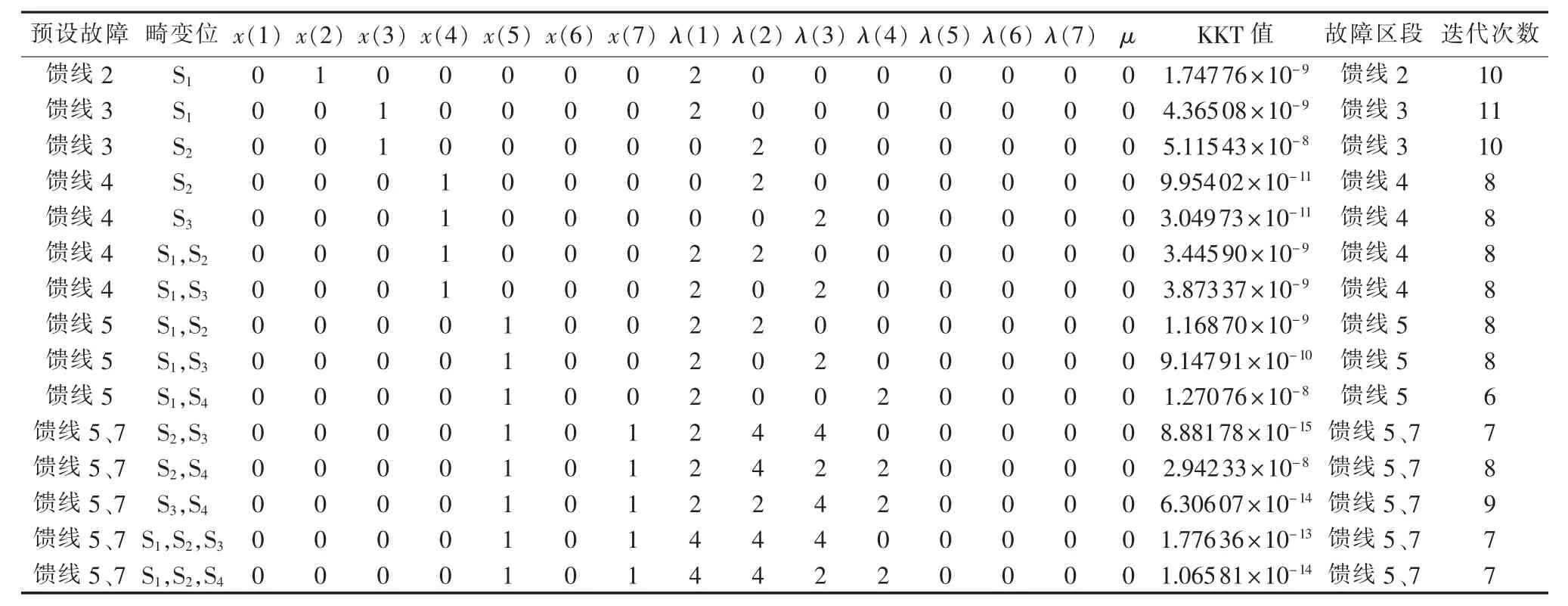
表5 信息畸变下的故障定位仿真结果Table 5 Simulative results of fault locating with information distortion

5 结论

a.采用代数关系描述构建配电网故障定位模型时，可克服传统基于逻辑关系描述方法故障定位时对群体智能算法的过分依赖。

b.在无信息畸变情况下，基于代数关系描述和因果关联设备特征构建的故障定位线性方程组模型能够实现对简单辐射状配电网馈线故障的准确定位，但其不具备容错性能；对含T型耦合节点配电网的多重故障进行定位时将会出现误判。但线性方程组模型避免了利用最优化算法的决策过程，只需对方程组进行求解，有利于提高故障定位效率，是构建具有高容错性故障定位方程组模型的基础。

c.本文利用互补约束条件、光滑互补函数和最优化极值理论构建的故障辅助因子数学模型，不仅实现了离散优化空间向连续寻优空间的等价影射变换，可避免直接对离散变量的优化决策，且以其为基础构建的非线性故障定位方程组模型在进行故障定位时，具有高容错性和强通用性，并能够实现多重馈线故障区段的准确辨识。

d.本文基于辅助因子的故障定位非线性方程组模型除可定位馈线故障区段外，在单一故障情况下可根据拉格朗日乘子的非零值来判定报警信息畸变位置，对于自动化终端设备的检修和维护具有一定的指导意义。

e.本文故障定位模型在求解时利用了牛顿-拉夫逊法的二阶收敛特征和并行迭代搜索特性，具有数值稳定性好、求解效率高的优势，可将本文提出的模型和算法应用于大规模配电网的故障定位。

参考文献：

［1］唐金锐，尹项根，张哲，等.配电网故障自动定位技术研究综述［J］.电力自动化设备，2013，33（5）：7-13.TANG Jinrui，YIN Xianggen，ZHANG Zhe，et al.Survey of fault location technology for distribution networks［J］.Electric Power Automation Equipment，2013，33（5）：7-13.

［2］张钊.配电网故障定位的通用矩阵算法［J］.电力自动化设备，2005，25（5）：40-42.ZHANG Zhao.General matrix algorithm for distribution system fault locating［J］.Electric Power Automation Equipment，2005，25（5）：40-42.

［3］刘耀湘，乐秀璠，顾欣欣.配电网故障区段判断和隔离的综合矩阵法［J］.电力自动化设备，2006，26（3）：38-40.LIU Yaoxiang，LE Xiufan，GU Xinxin.Synthesis matrix algorithm for fault section detection and isolation in distribution system［J］.Electric Power Automation Equipment，2006，26（3）：38-40.

［4］徐青山，唐国庆，张欣.计及容错的配电网故障定位新算法［J］.电力自动化设备，2005，25（6）：31-33.XU Qingshan，TANG Guoqing，ZHANG Xin.Error-tolerated fault locating algorithm of power distribution network［J］.Electric Power Automation Equipment，2005，25（6）：31-33.

［5］梅念，石东源，杨增力，等.一种实用的复杂配电网故障定位的矩阵算法［J］.电力系统自动化，2007，31（10）：66-70.MEI Nian，SHI Dongyuan，YANG Zengli，et al.A practical matrixbased fault location algorithm for complex distribution network［J］.Automation of Electric Power Systems，2007，31（10）：66-70.

［6］杜红卫，孙雅明，刘弘靖，等.基于遗传算法的配电网故障定位和隔离［J］.电网技术，2000，24（5）：52-55.DU Hongwei，SUN Yaming，LIU Hongjing，et al.Fault section diagnosis and isolation of distribution networks based on genetic algorithm［J］.Power System Technology，2000，24（5）：52-55.

［7］卫志农，何桦，郑玉平.配电网故障区间定位的高级遗传算法［J］.中国电机工程学报，2002，22（4）：127-130.WEI Zhinong，HE Hua，ZHENG Yuping.A refined genetic algorithm for the fault sections location ［J］.Proceedings of the CSEE，2002，22（4）：127-130.

［8］关龙，刘志刚，何士玉，等.离散二进制粒子群算法在基于模型配电网故障诊断中的应用［J］.电力自动化设备，2013，33（9）：89-92.GUAN Long，LIU Zhigang，HE Shiyu，et al.Application of BPSO algorithm in model-based fault diagnosis of distribution network［J］.Electric Power Automation Equipment，2013，33（9）：89-92.

［9］胡非，刘志刚，何士玉，等.一种基于模型的配电网故障诊断搜索算法［J］.电力自动化设备，2013，33（1）：81-90.HU Fei，LIU Zhigang，HE Shiyu，et al.Model-based search algorithm of fault diagnosis for distribution system［J］.Electric Power Automation Equipment，2013，33（1）：81-90.

［10］郭壮志，吴杰康.配电网故障区间定位的仿电磁学算法［J］.中国电机工程学报，2010，30（13）：34-40.GUO Zhuangzhi，WU Jiekang.Electromagnetism-like mechanism based fault section diagnosis for distribution network［J］.Proceedings of the CSEE，2010，30（13）：34-40.

［11］郑涛，潘玉美，郭昆亚，等.基于免疫算法的配电网故障定位方法研究［J］.电力系统保护与控制，2014，42（1）：77-83.ZHENG Tao，PAN Yumei，GUO Kunya，et al.Fault location of distribution network based on immune algorithm［J］.Power System Protection and Control，2014，42（1）：77-83.

［12］付家才，陆青松.基于蝙蝠算法的配电网故障区间定位［J］.电力系统保护与控制，2015，43（16）：100-105.FU Jiacai，LU Qingsong.Fault sections location of distribution network based on bat algorithm［J］.Power System Protection and Control，2015，43（16）：100-105.

［13］刘蓓，汪沨，陈春，等.和声算法在含DG配电网故障定位中的应用［J］.电工技术学报，2013，28（5）：280-286.LIU Bei，WANG Feng，CHEN Chun，etal.Harmonysearch algorithm forsolving faultlocation in distribution networks with DG［J］.Transactions of China Electrotechnical Society，2013，28（5）：280-286.

［14］张杰，邢丽君.线性代数［M］.北京：中国电力出版社，2016：75-87.

［15］LUO Z Q，PANG J S，RALPH D.Mathematical programs with equilibrium contraints［M］.Cambridge，UK：Cambrige University Press，1996：271-358.

［16］FERRIS M C，PANG J S.Engineering and economic applications of complementarity problems［J］.SIAM Review，1997，39（4）：669-713.

［17］YIN H X，ZHANG J Z.Global convergence of a smooth approximation method for mathematical with complementarity constraints［J］.Mathematical Methods of Operations Research，2006，64：255-269.

［18］HUANG Z H，QI L Q，SUN D F.Sub-quadratic convergence of a smoothing Newton algorithm for the P0-and monotone LCP［J］.Mathematical Programming，2004，99（3）：423-441.

［19］令锋，傅守忠，陈树敏，等.数值计算方法［M］.北京：国防工业出版社，2012：30-50.