考虑N-1安全的分布式电源多目标协调优化配置

刘 佳 ，徐 谦 ，程浩忠 ，兰 洲 ，马则良 ，朱忠烈

（1.上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240；2.国网浙江省电力公司经济技术研究院，浙江 杭州 310008；3.国家电网公司华东分部，上海 200120）

0 引言

近年来，智能电网概念的提出给传统配电网带来了显著的改变。作为发、输电系统和终端用户间的重要环节，配电网正逐步实现配电自动化，快速的网络转供能力将是未来智能配电网的主要特征。与此同时，配电网层面正接入大量以风电WTG（Wind Turbine Generation）和光伏发电 PVG（PhotoVoltaic Generation）为代表的分布式电源DG（Distributed Generation），面临着前所未有的不确定外部环境［1］。DG接入配电网运行能够起到降低电能损耗、改善电能质量和减少环境污染等作用［2］，然而，由于DG出力具有波动性、间歇性的特点，若其接入配电网的位置及容量不合适，将会影响到配电网的正常运行。因此，有必要对接入配电网的DG进行选址定容优化，以确保配电网的安全性、经济性。

目前，国内外学者已对DG选址定容规划问题进行了大量的研究并取得了一定的成果［2-8］。文献［2］研究了综合考虑配电公司、DG投资商和公共社会三者之间利益的含电动汽车DG规划模型，并采用改进自适应遗传算法（GA）加以求解；文献［3］提出了考虑节点电压和支路电流约束的PVG最大准入容量计算方法；文献［4］以配电网损耗最小为目标建立了含WTG、PVG的可再生DG选址定容模型，并采用混合整数规划法进行求解；文献［5］从优化投资及运行成本、网损、电压及电压稳定性3个角度建立了DG规划模型，并利用改进多目标粒子群优化（PSO）和模糊多权重算法求解规划方案；文献［6］建立了综合考虑WTG、PVG、微型燃气轮机和电动汽车等多种DG的规划模型，并利用遗传算法求解；文献［7］给出了配电网分布式风电源机会约束规划模型，并利用混合蛙跳法对模型加以求解；文献［8］则建立了多场景多时段下的DG优化配置模型。

现有文献均是从不同角度出发，建立N安全下的DG选址定容规划模型，并采用不同算法加以求解，而考虑到N-1安全准则是配电网规划中的重要准则，因此现有模型所得DG选址定容规划方案未必满足N-1安全，同时，对于配电网而言，主变、馈线N-1故障也属于不确定因素范畴，而现有模型中的不确定因素建模仅包含负荷、DG出力等正常工况下的不确定性，不确定性的内涵亟待完善。综上所述，有必要在DG规划阶段考虑N-1安全。

在安全分析方面，现有方法一般都基于N-1仿真［9］。但用这些方法进行逐个元件N-1校验速度慢且难以对系统的整体运行状态给出评价。为快速、定量刻画配电网中各工作点的安全裕度，配电网安全距离（DSSD）模型为一种分析配电网安全性、衡量裕度大小的新方法［10-12］。文献［10］提出了配电网安全域的概念、模型、安全边界的拓扑性质和安全评价与控制策略；文献［11］分析了供电能力和安全域理论在配电网在线安全监控中的作用，提出了相应的预防性控制、预测性控制和优化控制措施；文献［12］以网损最小和安全距离均衡比最小为目标建立了智能配电网动态重构模型。然而，现有关于DSSD的文献均尚未考虑含DG的配电网动态安全分析，难以直接指导DG规划以保证N-1安全。

为弥补现有DG选址定容规划方法的不足，本文考虑风光荷相关性，提出了一种考虑N-1安全的多目标DG选址定容规划模型，完善了配电网不确定因素的内涵。算例仿真结果表明，本文DG规划模型所得规划方案在保证N-1安全的前提下，实现了经济性、安全性下的最优，具有安全裕度高、裕度可测、负荷扩展能力强的特点。

1 配电网N-1安全评估方法

1.1 DSSD模型

1.1.1 配电网安全域

配电网安全域是在配电网主变N-1和线路N-1的约束下，配电网能够安全运行的所有工作点的集合［11］。其定义在馈线段负荷的工作点向量；考虑馈线出口负荷计算方程、馈线N-1约束、主变N-1馈线负荷转带约束、主变-馈线负荷等式约束、主变N-1主变容量约束和节点电压约束。基于交流潮流的配电网安全域ΩDSSR具体可表述为：

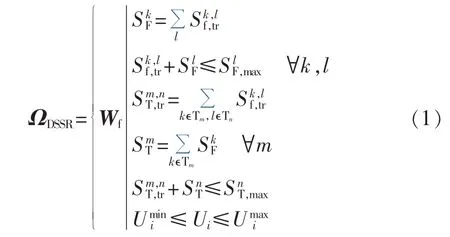
其中，Wf为基于馈线段负荷的工作点向量为馈线段 Fk所带负荷为馈线段 Fk发生 N-1 时转带给馈线段 Fl的负荷量为馈线段 Fl的容量为主变Tm发生N-1转带给主变Tn的负荷量为主变Tn所带的负荷；kϵTm表示馈线段Fk出自主变Tm对应的母线为主变 Tn的额定容量和分别为节点i的电压及其上、下限。

1.1.2 配电网安全边界

配电网安全边界是由所有恰好满足N-1安全的临界工作点组成的一系列线性超平面。安全边界具有以下3个性质［10］：存在性，配电网N-1安全边界是存在的；线性，配电网安全边界由线性的、紧致的且不会“打结”的超平面精确描述；连通性，安全边界围成的区域是连通的、内部无空洞的凸集。

1.1.3 DSSD

工作点在配电网安全域中的位置可以反映系统N-1安全性，并利用安全距离来量化反映该数据［10］。安全距离是指当前工作点到各配电网安全边界的欧氏距离，其具体计算方法已在文献［10］中定义，在此不再赘述。当工作点不满足N-1安全时，安全距离为负值，绝对值越大，此工作点不安全程度越高；当工作点满足N-1安全时，安全距离为正值，绝对值越大，此工作点安全程度越高。

1.2 安全裕度指标

本文选用以下3个N-1安全裕度指标［12］。

a.安全距离均值VMSD：各条安全距离的平均值，以表征全网安全距离的平均水平。VMSD越大，表示各条安全距离平均水平越高，全网安全裕度越大；反之，全网安全裕度越小。具体计算公式为：

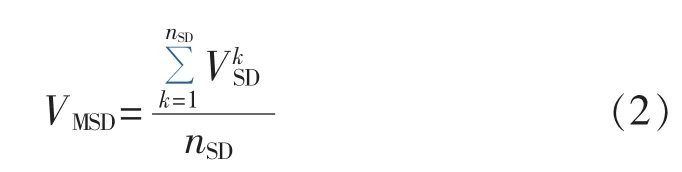
其中为第k条安全距离的值；nSD为安全距离条数。

b.安全距离均衡度VEDSD：各条安全距离方差，以表征全网安全距离的离散程度。VEDSD越小，表示各条安全距离越均衡，在各馈线、主变容量近似相等的前提下，各馈线出口负荷越均匀，各馈线、主变负载率差异性越小，全网安全裕度越大；反之，全网安全裕度越小。具体计算公式为：

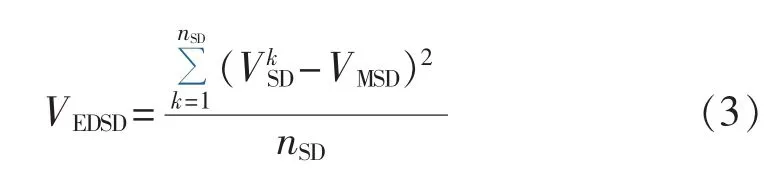
c.安全距离均衡比VERSD：安全距离均衡度和安全距离均值之比，以表征各安全距离的偏差与均值的相对数值关系。考虑到各安全距离的偏差越小、均值越大，全网安全裕度越大，因此，VERSD越小，系统安全性越好。具体计算公式为：

2 考虑相关性的风光荷概率建模

2.1 WTG出力概率模型

风速通常采用双参数Weibull分布来描述［2］：

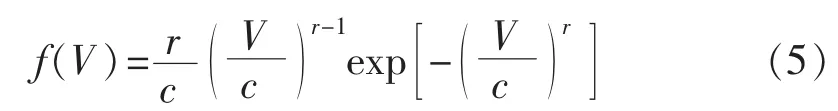
其中，V为WTG叶轮轮毂处的风速；r和c分别为形状参数和尺度参数。

本文的WTG采用恒功率因数控制，则WTG出力SWTG与风速V间的关系可近似用分段函数表示［13］：

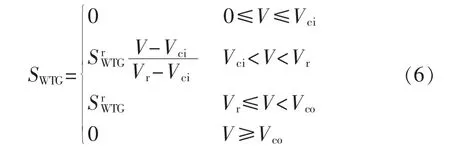
其中为 WTG 的 额 定 容 量；Vci、Vr、Vco分 别 为WTG的切入风速、额定风速、切出风速。

2.2 PVG出力概率模型

光照强度通常采用Beta分布来描述［14］：

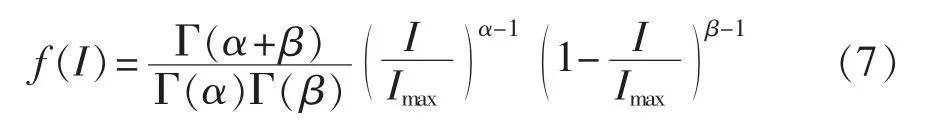
其中，I和Imax分别为光照强度及其最大值；α和β为Beta分布的2个参数；Γ（·）为伽马函数。

本文的PVG采用恒功率因数控制，则PVG出力SPVG与光照强度I之间的关系可近似表示为［14］：

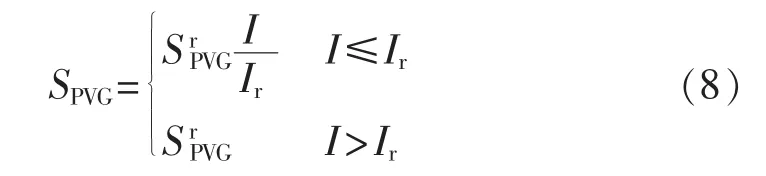
其中为PVG的额定容量；Ir为额定光照强度。

2.3 负荷概率模型

负荷值通常采用正态分布来描述［14］：

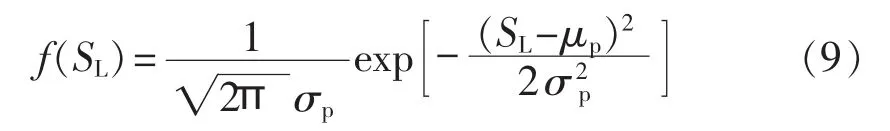
其中，SL、μp和σp分别为负荷的随机量、期望和标准差。

2.4 风光荷相关性样本矩阵生成

对于含风速、光照强度和负荷的3维随机变量X=［X1，X2，X3］T，设其相关系数矩阵为［ρij］3×3，其中相关系数ρij的定义如式（10）所示。

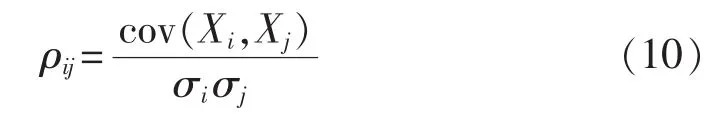
其中，σi和 σj分别为 Xi和 Xj的标准差；cov（Xi，Xj）为变量 Xi、Xj的协方差。

本文采用基于Sobol序列的准蒙特卡洛模拟QMCS（Quasi Monte Carlo Simulation）进行样本采样［15］。同时，考虑到相关系数矩阵非正定或非满秩，其Cholesky分解不存在，而由于相关系数矩阵均为对称阵，其奇异值分解一直存在，因此，本文采用奇异值分解来对相关系数矩阵进行处理［16］。QMCS联合奇异值分解能够产生目标相关系数矩阵ρobj下的待采样随机变量的样本矩阵，其理论依据可参见文献［16］。

应用QMCS和奇异值分解产生相关性DG出力矩阵的具体过程如下。

a.设采样规模为N0，利用QMCS对风速、光照强度和负荷进行采样，得到一个3×N0阶的初始样本矩阵 S0。

b.随机生成一个3×N0阶的顺序矩阵L，并按照式（10）计算L的相关系数矩阵ρL。

c.按照式（11）对ρL进行奇异值分解，并通过式（12）来消除由于随机排列而产生的相关性。

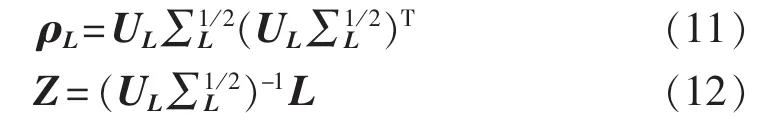
其中，UL为由矩阵ρL奇异值分解得到的酉矩阵；∑L为由矩阵ρL的奇异值构成的对角矩阵；Z为中间矩阵。

d.按照式（13）对目标相关系数矩阵ρobj进行奇异值分解，并通过式（14）令Zu的相关系数矩阵与ρobj近似相等。

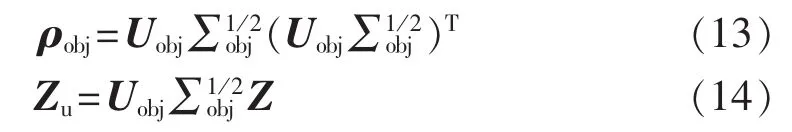
其中，Uobj为由矩阵ρobj奇异值分解得到的酉矩阵；∑obj为由矩阵ρobj的奇异值构成的对角矩阵。

e.更新S0中的元素得到新的样本矩阵Su。

经过以上操作，就产生了采样规模为N0且含风速、光照强度和负荷的相关性样本矩阵Su，其中，每一行样本数据表示对应变量的时间序列值，而每一列样本数据则表示该场景下的风光荷数值。最后，按照式（6）和式（8）进一步将Su中的风速和光照强度转换为WTG和PVG出力。

3 考虑N-1安全的DG规划模型

3.1 目标函数

以年综合费CSUM（包括DG投资费CI、DG运行维护费COM和配电网向上级电网购电费CP）最小和安全距离均衡比VERSD最小为目标，用机会约束规划方法［17］建立多目标DG选址定容规划模型，具体如下：

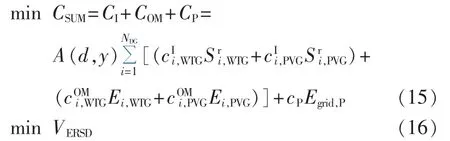
其中，A（d，y）=d（1+d）y／［（1+d）y-1］为现值转等年值系数，d为贴现率，y为设备使用年限；NDG为DG待选安装节点个数；cIi，WTG和 cIi，PVG分别为安装在待选节点i的WTG和PVG的单位容量投资成本；Sri，WTG和Sri，PVG分别为安装在待选节点i的WTG和 PVG的额定容量；cOMi，WTG和 cOMi，PVG分别为安装在待选节点 i的 WTG 和 PVG 的单位运行维护费；Ei，WTG和 Ei，PVG分别为安装在待选节点i的WTG和PVG的年发电量；cP为配电网向上级电网购电的单位成本；Egrid，P为年购电量。

3.2 约束条件

a.潮流方程约束。

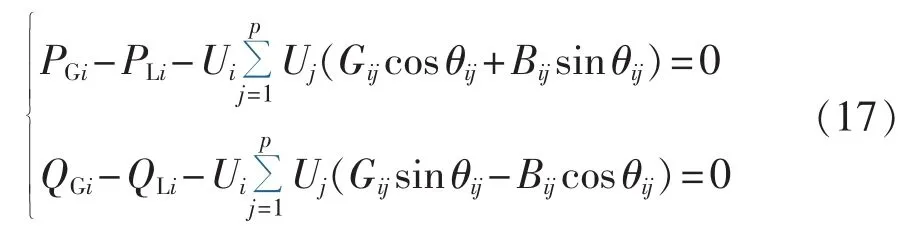
其中，PGi和QGi分别为节点i发出的有功功率和无功功率；PLi和QLi分别为节点i的有功需求和无功需求；Ui和Uj分别为节点i和j的电压幅值；Gij为支路电导；Bij为支路导纳；θij为节点i与节点j电压相角差；p为与节点i相关联的支路数。

b.待选安装节点的DG容量约束。

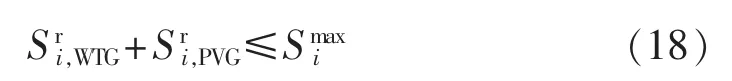
其中为待选安装节点i所允许的DG容量上限。

c.WTG和PVG容量的离散性约束。

其中分别为待选安装节点 i的单台WTG和PVG的额定容量；ai和bi分别为待选安装节点i的WTG和PVG的数量。

d.N-1安全约束。

e.节点电压机会约束。

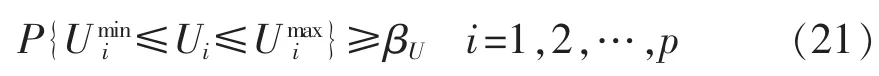
其中，P｛·｝为｛·｝中事件成立的概率； βU为满足节点电压约束的置信水平。

4 求解算法和步骤

本文采用正态边界交点NBI（Normal Boundary Intersection）和动态小生境差分进化算法DNDEA（Dynamic Niche Differential Evolution Algorithm）相结合的策略对所提选址定容规划模型进行求解。考虑到该模型属于整数非线性多目标规划问题，该算法既充分考虑了年综合费和安全距离均衡比2个目标之间的互相制约关系，避免了确定两者相对权重的主观性，又克服了差分进化算法DEA（Differential Evolution Algorithm）在初期搜索速度快、后期易陷入局部最优点的缺点。

4.1 NBI

NBI是由Das和Dennis于1998年提出的一种生成均匀Pareto前端解集的有效方法［18-19］。其基本思想是：首先，利用映射矩阵将设定的权重向量映射到目标空间进行坐标变换；然后，将两目标空间之间的乌托邦线N等分，第q个等分点在法向量方向进行投影形成Pareto曲面；最后，根据Pareto最优性条件，即最大化法向量到Pareto曲面交点处的截距，所得的解就是Pareto前端解集。其具有以下主要优点：各目标函数相对独立，可获得离散Pareto最优解集；通过跟踪灵敏度曲线保证连续性算法计算效率。

4.2 DNDEA

DEA［20］是由 Store和 Price于 1995年提出的一种群体性智能算法。DEA的基本过程可参见文献［20］，这里不再赘述。其基本思想是从某一随机产生的初始种群出发，通过变异、交叉和选择等进化操作，淘汰劣质个体、保留优良个体，不断地进行迭代进化，逐渐向最优解逼近，直到满足收敛条件。

为了增加DEA对问题解空间的搜索性能，引入动态小生境机制［21］，得到DNDEA。动态小生境机制能使得进化初期的个体都具有较大的差异，种群拥有非常大的多样性，从而利于初期的全局搜索；同时也能增强进化后期的局部搜索，提高算法的精度［21］。

4.3 求解步骤

基于NBI联合DNDEA的混合策略求解多目标DG选址定容规划模型流程见图1。具体过程如下。

a.置迭代次数i=1。

b.初始化DNDEA种群。按照式（22）的编码方式对DNDEA中的个体进行十进制编码，随机产生Np个初始个体。其中，每个个体代表一种DG配置方案。

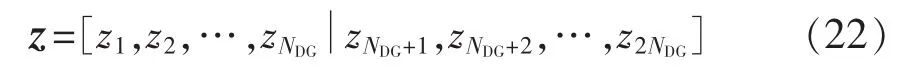
其中，前NDG个变量和后NDG个变量分别为各待选节点WTG和PVG的安装数量。

c.计算初始种群分别相对于单目标函数CSUM和VERSD的适应度值。

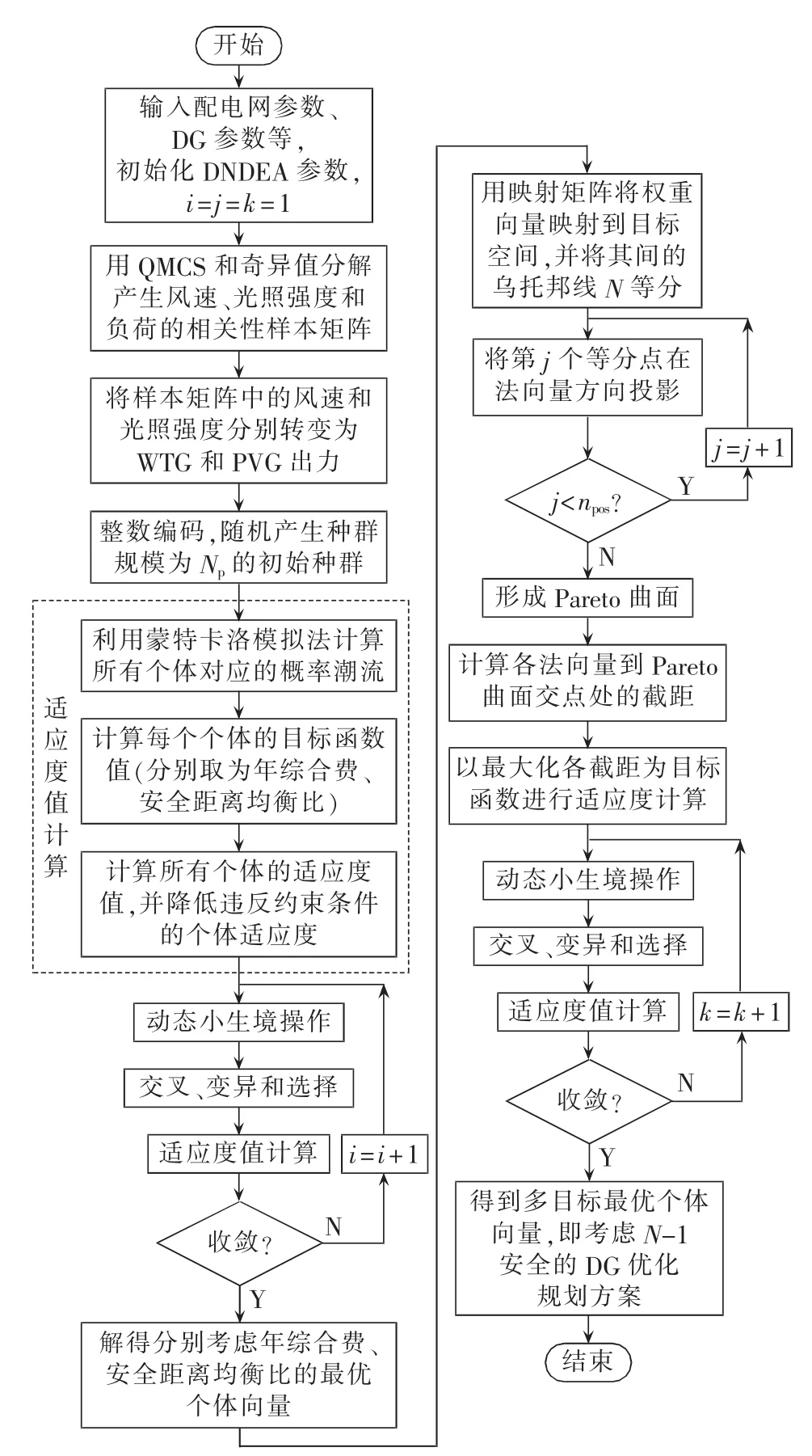
图1 NBI联合DNDEA求解规划模型流程图Fig.1 Flowchart of planning model solver based on NBI and DNDEA

d.进化操作产生新种群。本文综合运用两轮联赛选择，两点交叉，单点均匀变异，交叉以及变异均采用不等概率，并引入精英保留策略和动态小生境机制。

e.计算新种群分别相对于单目标函数CSUM和VERSD的适应度值。

f.判断DNDEA是否收敛，若收敛，则分别输出相对于单目标函数CSUM和VERSD的结果，并退出循环；否则转步骤d。

g.更新迭代次数：i=i+1。

h.用 NBI将多目标模型式（15）—（21）转换为法向量到Pareto曲面交点处的截距最大化的单目标模型。

i.仿照步骤a—g，利用DNDEA求解步骤h中建立的单目标模型，得到Pareto前端解集。

5 算例分析

5.1 算例基本情况

算例配电网如图2所示，共有3座33kV变电站、6台主变压器、20条11 kV馈线和104个负荷节点，各节点负荷类型均相同且功率因数为0.85。两相邻负荷节点间线路长度均为1 km。算例中，各主变及馈线数据、联络线数据、节点负荷均值数据见表1—3。负荷的标准差为均值的10%。

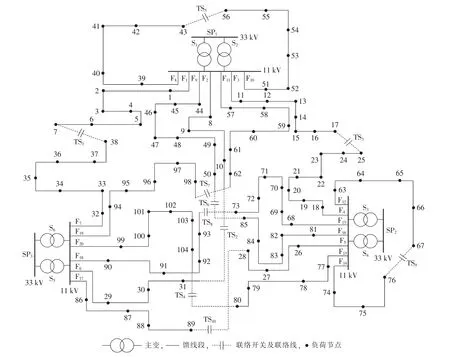
图2 算例网络Fig.2 Case system

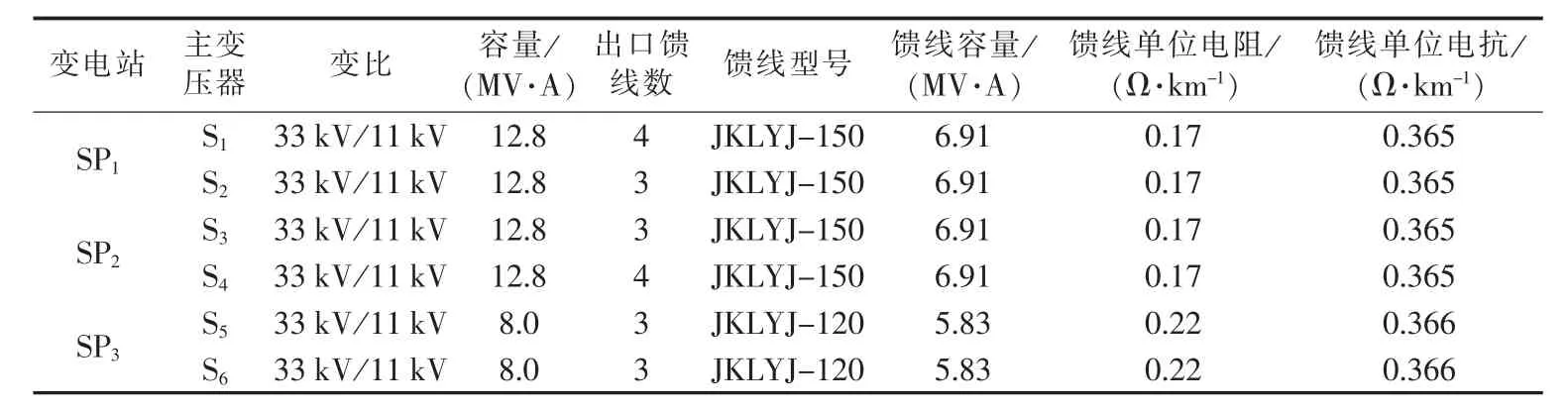
表1 各主变及馈线数据Table1 Data of main transformers and feeders

部分规划参数如下：DG的待选安装节点为3、5、7、10、39、41、43、45、47 和 49，每个待选安装节点所允许安装的DG容量上限为2 MW。单台WTG的额定容量为0.5 MW，切入风速、额定风速、切出风速分别为 3、13、20 m／s；WTG 的单位容量投资费为1500000$／MW，单位发电量的运行维护费用为30$／（MW·h）；风速服从 r＝2.15 和 c＝8.32的 Weibull分布。单个PVG的额定容量为0.5 MW，额定光照强度为 0.5 kW／m2，最大光照强度为 0.6 kW／m2；PVG 的单位容量投资费为1750000$／MW，单位发电量的运行维护费为 40$／（MW·h）；光照强度服从 α＝0.55和β＝1.38的Beta分布。WTG和PVG的使用年限均为20 a，贴现率为 0.06。置信水平 βU＝0.95；节点电压所允许的范围为0.95～1.05 p.u.。配电网向上级电网购电的单位成本为 50$／（MW·h）。NBI的参数为：等分点个数为20。DNDEA的参数为：最大迭代次数为50，种群规模为100，缩放因子和交叉率均从0.9线性递减到0.1。

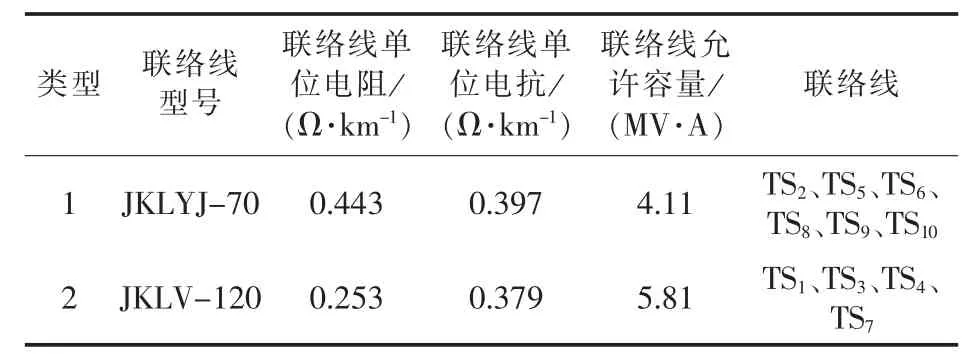
表2 联络线数据Table 2 Data of tie lines

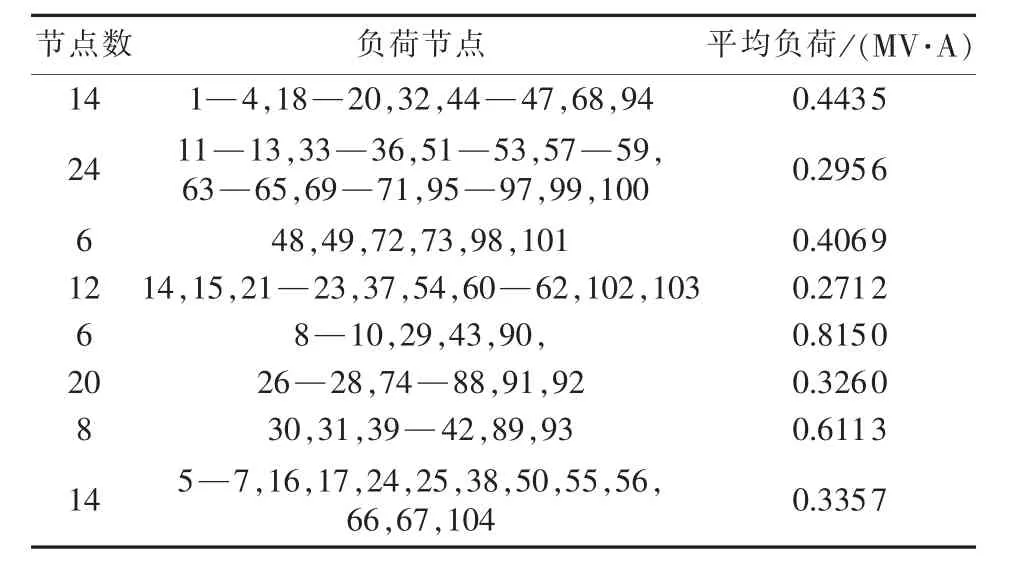
表3 节点负荷均值数据Table 3 Data of nodal average loads

基于相关性样本数据，图3给出了该配电网所在区域的风速、光照强度和负荷（标幺值）的年变化曲线。本文所有仿真的计算条件是：计算机CPU为i7-3820，主频为 3.6 GHz，内存为 8 GB，在 MATLAB 2013a平台上编制计算程序。

5.2 算例计算结果及分析

将本文所提出的模型用于算例研究，并采用NBI联合DNDEA对规划模型进行求解，得到考虑N-1安全的DG最优规划方案如表4所示。作为对比，表4中同时给出了不考虑N-1安全，即仅以年综合费最小为目标函数的DG规划结果。

由表4可以看出，DG规划模型中考虑N-1安全将会对结果产生影响，而综合考虑配电网经济性、安全性，本文所提出的模型更优。解释其原因如下：从安全性角度来看，较不考虑N-1安全模型，本文模型所得DG规划方案的安全距离均值大了1.02%，表明安全裕度平均水平较大；安全距离均衡度小了11.97%，表明净负荷分布更加平均，各主变、馈线负载率更均衡，安全距离均衡比小了12.76%，综合说明系统安全性更好；从经济性角度来看，相比于不考虑N-1安全的DG规划，本文模型所得规划方案虽需多安装1台WTG，但年综合费较之相当，仅多出0.55%；综合考虑经济性、安全性，由于年综合费和安全距离均衡比的量纲不同，这里采用百分比大小比较对不同方案优劣性进行评价，考虑到本文模型所得DG规划方案的安全距离均衡比小了11.97%，年综合费仅多了0.55%，兼顾系统经济性、安全性，本文模型更优。

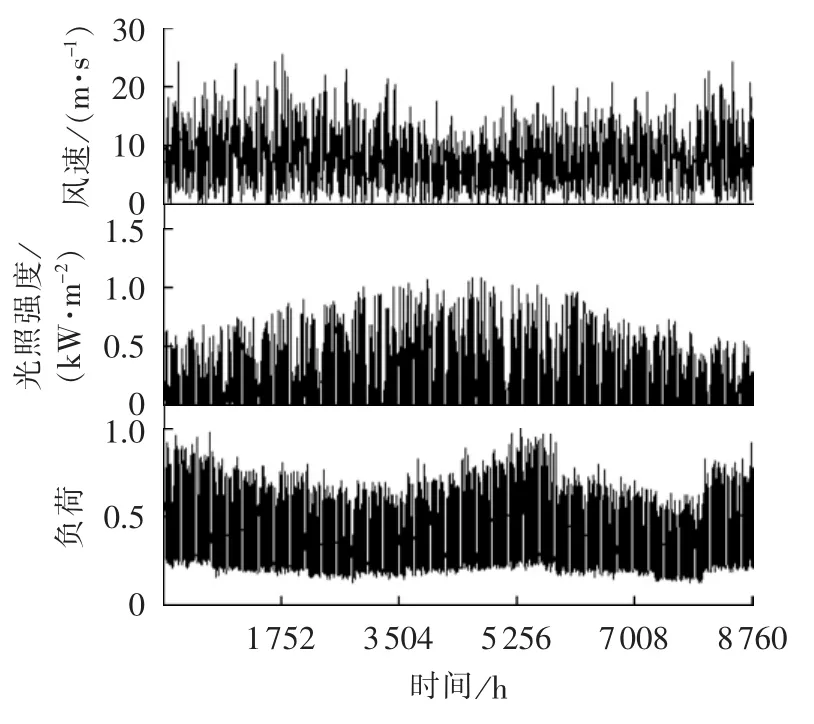
图3 风速、光照强度和负荷的年变化曲线Fig.3 Curves of annual wind speed，llumination intensity and load

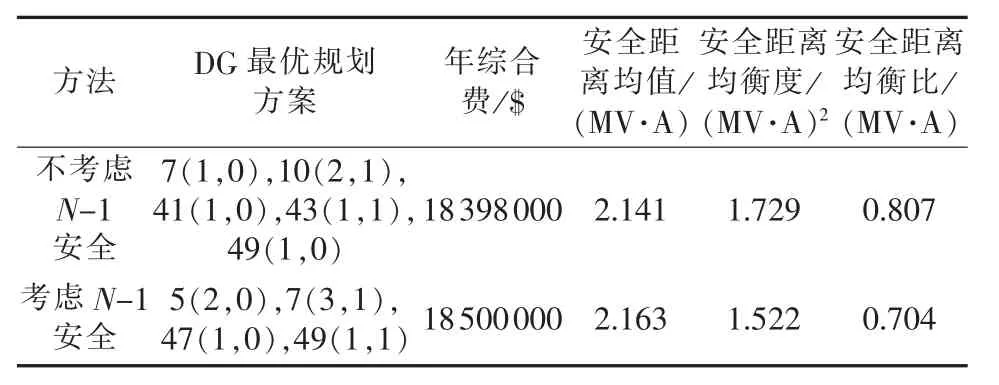
表4 DG最优规划方案Table 4 Optimal DG planning schemes

5.3 N-1安全下的DG配置作用分析

为了分析N-1安全下的DG作用，本文比较了DG规划前、不考虑N-1安全的DG规划和考虑N-1安全的DG规划3种情景所对应配电网中各条安全距离情况，具体如图4所示。

由图4可看出，对于DG规划前，第1条和第16条安全距离为负值，由于安全距离的大小与主变容量、馈线容量和馈线负荷水平三者的匹配有关，说明此时馈线段F1和馈线段F16的负荷较重，与之相比，第12和14条安全距离为正值且相差很大，说明原配电网负荷分布不匀，局部馈线负荷重、轻载情况较为严重；对于不考虑N-1安全的DG规划，第16条安全距离变为正值，说明配电网中各馈线负荷重、轻载情况有所改善，分析其原因是由于在节点49接入了一台WTG，使得由馈线段F9和馈线段F16构成的联络净负荷水平下降，第16条安全距离增大。然而，第1条安全距离依旧为负值，说明经DG规划后，仍不满足N-1安全的要求，仅是系统经济性得到了优化改善；而对于考虑N-1安全的DG规划，不仅使第1条和第16条安全距离均变为正值，满足了N-1安全准则，而且配电网中各安全距离均值水平、均衡度均得到了相应改善，全网安全裕度水平得到了提高。

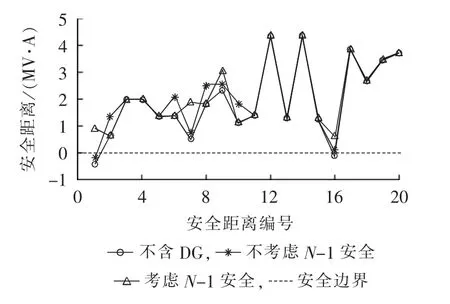
图4 安全距离情况Fig.4 Security distances

需说明的是，第11条到第15条安全距离在考虑N-1安全前后未发生改变是由于本文选取的DG待选安装节点没有位于这些馈线或与这些馈线联络的馈线上，若需改善，仅需扩充DG待选安装节点集并建模求解，这里不再赘述；同时，各安全距离没有彻底实现均衡是由算例电网拓扑结构不对称及各主变、馈线容量和馈线负荷存在差异性共同导致的。

在不考虑N-1安全和考虑N-1安全2种规划情景下，分别对算例系统中的各节点电压水平进行校验。非DG待选安装馈线段上的各节点电压均在允许范围内，而 DG待选安装馈线段 F1、F2、F8和 F9上的各节点电压水平如图5所示，图中节点电压为标幺值，后同。

由图5可以看出，对于不考虑N-1安全的DG规划，节点49、50的电压低于节点允许电压下限，而与之相较，考虑N-1安全的DG规划能保证各节点电压均在允许上下限内。因此，考虑N-1安全有助于提高满足节点电压机会约束的概率。

为进一步分析节点49和50的电压越限概率，图6给出了节点49和50的电压概率分布曲线。

由图6可以看出，考虑N-1安全下的节点49和50的电压期望值分别为0.964 0 p.u.和0.9613 p.u.，满足节点电压约束下限，但不考虑N-1安全下的节点49和50的电压越下限概率分别达到51%和55%。因此，不考虑N-1安全会增加系统运行的风险。而考虑N-1安全使得节点49和50的电压方差减小，概率分布较好地满足了机会约束。

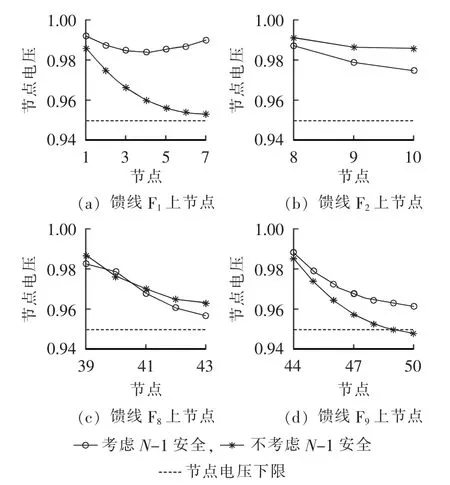
图5 有无考虑N-1安全的各节点电压水平Fig.5 Comparison of nodal voltage between schemes with and without N-1 security

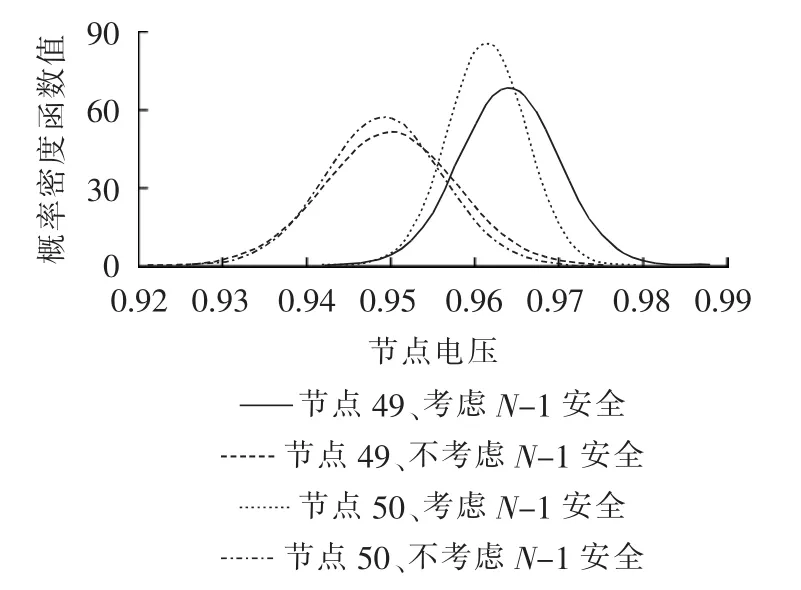
图6 有无考虑N-1安全的节点49和50电压概率分布Fig.6 Comparison of voltage probability distribution between schemes with and without N-1 security for Node 49 and 50

此外，由表4和图4、图5可以看出，就馈线层面而言，对于不考虑N-1安全的DG规划，第1条安全距离为负是由于在馈线段F1上仅配置了0.5 MW的DG，而对于考虑N-1安全的DG规划，第1条安全距离为正则是通过在馈线段F1上配置3 MW的DG；就节点层面而言，对于不考虑N-1安全的DG规划，存在2个不满足电压约束的节点是由于仅在馈线段F9上的节点49接入了0.5 MW的DG，而对于考虑N-1安全的DG规划，所有节点均满足电压约束是由于馈线段F9上共配置了1.5 MW的DG，其中，节点49接入了1 MW的DG。综上，说明通过将安全距离均衡比引入目标函数，具有指导DG选址定容以优化系统安全性的作用。分析其原因如下：DG规划前，馈线负载率高的馈线，其安全距离小；馈线负载率低的馈线，其安全距离大，而将安全距离均衡比作为目标函数纳入DG规划模型，通过DG的选址定容，改善各节点净负荷分布，使得各条安全距离更加均衡，系统安全性更好。

与本文模型相比，传统以经济性最优的选址定容规划模型，DG接入供电路径较短线路的概率较大，若此时线路轻载，则线路节点电压越上限的概率大幅增加，加之DG接入容量不适宜，配电网潮流反向，安全距离随DG出力的增加而减小甚至越过安全边界，使得系统N-1安全无法保障。可见，在保证系统经济性的前提下，考虑N-1安全的DG规划具有重要意义。

5.4 算法效率分析

为衡量算法寻优的效率及鲁棒性，在相同种群规模下，分别采用PSO算法、GA、DEA和DNDEA求解第3节中模型50次，所得最小年综合费CminSUM、平均年综合费CSUM、最小安全距离均衡比VminERSD、平均安全距离均衡比VERSD、达到CminSUM和VminERSD次数N1、平均迭代次数N2、平均计算时间t¯列于表5中。其中，PSO算法的参数为：最大迭代次数为50，粒子数为100，惯性权重从0.9线性递减到0.1，局部与全局学习因子为2，粒子最大移动距离为5。GA的参数为：最大迭代次数为50，染色体数为100，交叉率从0.9线性递减到0.1，变异率从0.09线性递减到0.01，采用轮盘赌选择机制。

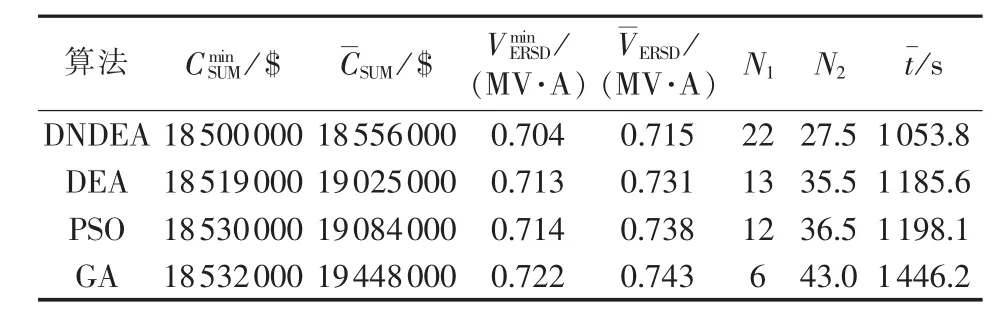
表5 各算法收敛特性对比Table 5 Comparison of convergence performances among various algorithms

由表5可以看出，4种算法所得结果相近，但DNDEA达到CminSUM和VminERSD的次数N1明显高于其他3种算法，平均迭代次数N2和平均计算时间 t¯则低于其他算法，这表明本文采用的DNDEA具有较高的寻优效率。此外，相比其他3种算法，DNDEA能够高效寻优的原因在于其引入了动态小生境机制，极大地增加了全局寻优能力。

6 结论

本文丰富了系统不确定性的内涵，提出了一种考虑N-1安全的多目标DG选址定容规划模型。所得DG规划方案实现了兼顾系统经济性、安全性下的最优，具有合理性和精度高的特点，可用于指导安全裕度要求较高的DG规划。本文得到的主要结论如下：

a.考虑DG出力低差异性和相关系数矩阵非正定，利用准蒙特卡洛模拟和奇异值分解生成风光荷相关性样本矩阵，以同时计及DG出力及时变负荷带来的不确定性及相关性；

b.以年综合费最小和安全距离均衡比最小为目标的DG规划模型，能够保证N-1安全，实现了系统经济性、安全性的综合优化；

c.本文采用的NBI联合DNDEA求解模型是有效的且寻优效率高于同样规模的PSO算法和GA。

参考文献：

［1］NAGATA T，SASAKI H，YOKOYAMA R.Power system restoration by joint usage of expert system and mathematical programming approach［J］.IEEE Transactions on Power Systems，1995，10（3）：1473-1479.

［2］李振坤，田源，董成明，等.基于随机潮流的含电动汽车配电网内分布式电源规划［J］. 电力系统自动化，2014，38（16）：60-66.LIZhenkun，TIAN Yuan，DONG Chengming，etal.Distributed generators programming in distribution network involving vehicle to grid based on probabilistic power flow［J］.Automation of Electric Power Systems，2014，38（16）：60-66.

［3］SHAYANI R A，DE OLIVEIRA M A G.Photovoltaic generation penetration limits in radial distribution systems［J］.IEEE Transactions on Power Systems，2011，26（3）：1625-1631.

［4］ATWA Y M，EL-SAADANY E F，SALAMA M M A，et al.Optimal renewable resources mix for distribution system energy loss minimization［J］.IEEE Transactions on Power Systems，2010，25（1）：360-370.

［5］栗然，马慧卓，祝晋尧，等.分布式电源接入配电网多目标优化规划［J］. 电力自动化设备，2014，34（1）：6-13.LI Ran，MA Huizhuo，ZHU Jinyao，et al.Multi-objective optimization for DG integration into distribution system［J］.Electric Power Automation Equipment，2014，34（1）：6-13.

［6］LIU Z，WEN F，LEDWICH G.Optimal siting and sizing of distributed generatorsin distribution systemsconsidering uncertainties［J］.IEEE Transactions on Power Delivery，2011，26（4）：2541-2551.

［7］张沈习，陈楷，龙禹，等.基于混合蛙跳算法的分布式风电源规划［J］. 电力系统自动化，2013，37（13）：76-82.ZHANG Shenxi，CHEN Kai，LONG Yu，et al.Distributed wind generation planning based on shuffled frog leaping algorithm［J］.Automation of Electric Power Systems，2013，37（13）：76-82.

［8］白晓清，赵瞻，鲍海波.基于CLARA算法的考虑时序特性分布式电源规划［J］. 电力自动化设备，2016，36（5）：14-22.BAI Xiaoqing，ZHAO Zhan，BAO Haibo.DG planning based on CLARA algorithm with consideration of timing characteristics［J］.Electric Power Automation Equipment，2016，36（5）：14-22.

［9］夏叶，康重庆，宁波，等.用户侧互动模式下发用电一体化静态安全校核［J］. 电力系统自动化，2012，36（9）：35-41.XIA Ye，KANG Chongqing，NING Bo，et al.Generation and load integrated static security checking on interaction mode on cus-tomer side［J］.Automation of Electric Power Systems，2012，36（9）：35-41.

［10］XIAO J，ZU G，GONG X，et al.Model and topological characteristics of power distribution system security region［J］.Journal of Applied Mathematics，2014，2014（6）：1-13.

［11］XIAO J，ZU G，GONG X，et al.Observation of security region boundary for smart distribution grid［J］.IEEE Transactions on Smart Grid，2017，8（4）：1731-1738

［12］刘佳，程浩忠，肖峻，等.计及N-1安全准则的智能配电网多目标重构策略［J］. 电力系统自动化，2016，40（7）：9-15.LIU Jia，CHENG Haozhong，XIAO Jun，et al.A multi-objective reconfiguration strategy for smart distribution network considering N-1 security criterion［J］.Automation of Electric Power Systems，2016，40（7）：9-15.

［13］赵渊，何媛，宿晓岚，等.分布式电源对配网可靠性的影响及优化配置［J］. 电力自动化设备，2014，34（9）：13-20.ZHAO Yuan，HE Yuan，SU Xiaolan，et al.Effect of distributed generation on power distribution system reliability and its optimal allocation［J］.Electric Power Automation Equipment，2014，34（9）：13-20.

［14］ZHANG S，CHENG H，ZHANG L，et al.Probabilistic evaluation of available load supply capability for distribution system ［J］.IEEE Transactions on Power Systems，2013，28（3）：3215-3225.

［15］SINGHEE A，RUTENBAR R.Why quasi-Monte Carlo is better than Monte Carlo or Latin hypercube sampling for statistical circuit analysis［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2010，29 （11）：1763-1776.

［16］方斯顿，程浩忠，徐国栋，等.基于非参数核密度估计的扩展准蒙特卡洛随机潮流方法［J］. 电力系统自动化，2015，39（7）：21-27.FANG Sidun，CHENG Haozhong，XU Guodong，et al.An extended quasi Monte Carlo probabilistic load flow method based on non-parametric kernel density estimation［J］.Automation of Electric Power Systems，2015，39（7）：21-27.

［17］周辛南，柯德平，孙元章.基于配电网静态电压质量机会性约束的可再生能源分布式发电容量规划［J］.电力自动化设备，2015，35（9）：143-149.ZHOU Xinnan，KE Deping，SUN Yuanzhang.DG planning based on chance constraint of distribution network static voltage quality for renewable energies［J］.Electric Power Automation Equipment，2015，35（9）：143-149.

［18］ROMAN C，ROSEHART W.Evenly distributed Pareto points in multi-objective optimal power flow［J］.IEEE Transactions on Power Systems，2006，21（2）：1011-1012.

［19］MAVALIZADEH H，AHMADI A，HEIDARI A.Probabilistic multiobjective generation and transmission expansion planning problem using normal boundary intersection［J］.IET Generation，Transmission&Distribution，2014，9（6）：560-570.

［20］STORN R，PRICE K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11（4）：341-359.

［21］DELLA C A，DE STEFANO C，MARCELLI A.Where are the niches？ Dynamic fitness sharing［J］.IEEE Transactions on Evolutionary Computation，2007，11（4）：453-465.